0xAlpha contributed to DODO research: Let us deeply analyze zk-SNARK technology and explore its principles and applications for privacy protection in encryption and blockchain.
Author: 0xAlpha Co-founder @DeriProtocol
Compiled by: DODO Research
Welcome to follow on Twitter: @0x_Alpha

0xAlpha contributed to DODO research. This article will mathematically decode this technology, revealing how it can prove the truth of knowledge without revealing any information. Get ready, let's unveil the mystery of zk-SNARK.
introduce
zk-SNARK, "zero-knowledge succinct non-interactive knowledge argument", enables a verifier to confirm that a prover possesses certain knowledge, called witness , that satisfies specific relationships without revealing the witness. any information itself.
Generating zk-SNARKs for a specific problem involves the following four stages:
- Convert a problem (or function) into an arithmetic gate circuit.
- This circuit is then translated into a matrix formula.
- This matrix formula is further converted into a polynomial that should be divisible by a specific minimum polynomial.
- Finally, this divisibility is expressed in elliptic curve points of a finite field, where the proof proceeds.
The first three steps merely transform the representation of the original statement. The last step uses homomorphic encryption to project the statements of step 3 into an encrypted space, allowing the prover to verify the mirror statements therein. Given that this projection utilizes asymmetric encryption, it is not feasible to backtrack from the statement in step 3 to the original statement, ensuring zero-knowledge exposure.
The mathematical background required to read this article is equivalent to first-level algebra for STEM majors. The only concept that might be challenging might be elliptic curve cryptography. For those unfamiliar with this, think of it as an exponential function with a special base, keeping in mind that its inverse remains unsolved.

In this article, we will continue to use equation (1) as the basis for our discussion.
Step 1: Arithmetic Gate Circuit
Equation (1) can be broken down into the following basic arithmetic operations:
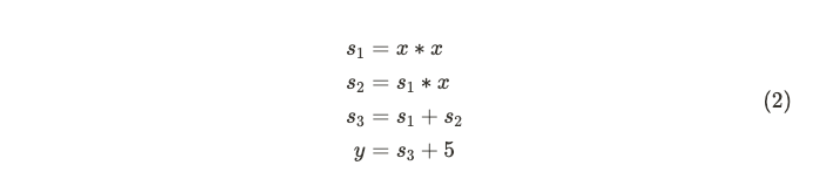
This corresponds to the following arithmetic gate circuit:
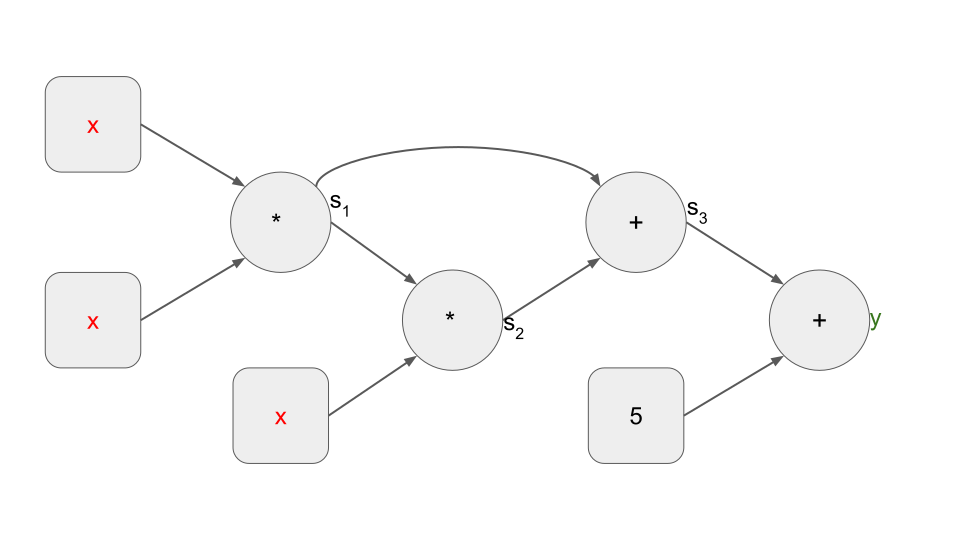
We also refer to Equation (2) as a set of four "first-level constraints", each constraint describing the relationship of an arithmetic gate in the circuit. In general, a set of n first-level constraints can be summarized as a quadratic arithmetic program (QAP), which is explained next.
Step 2: Matrix
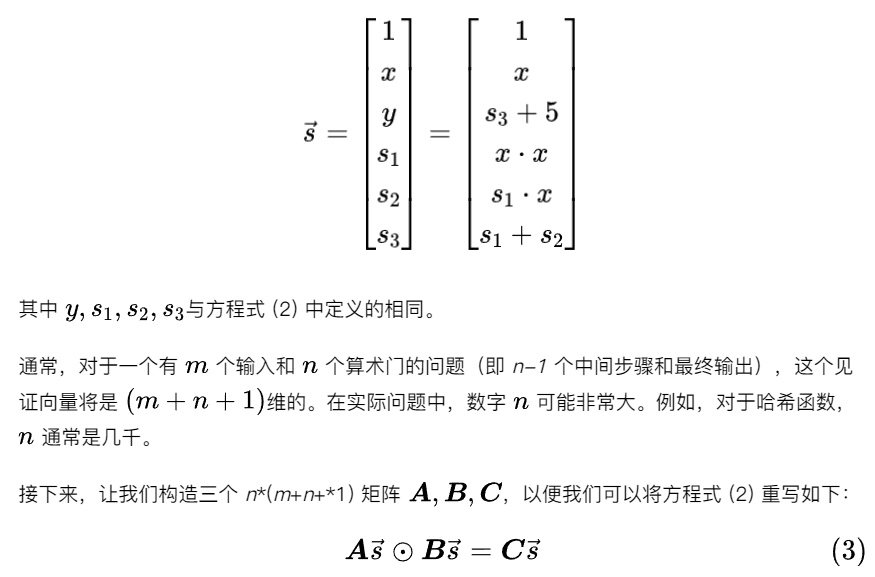
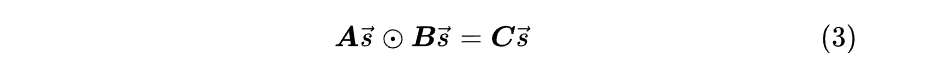
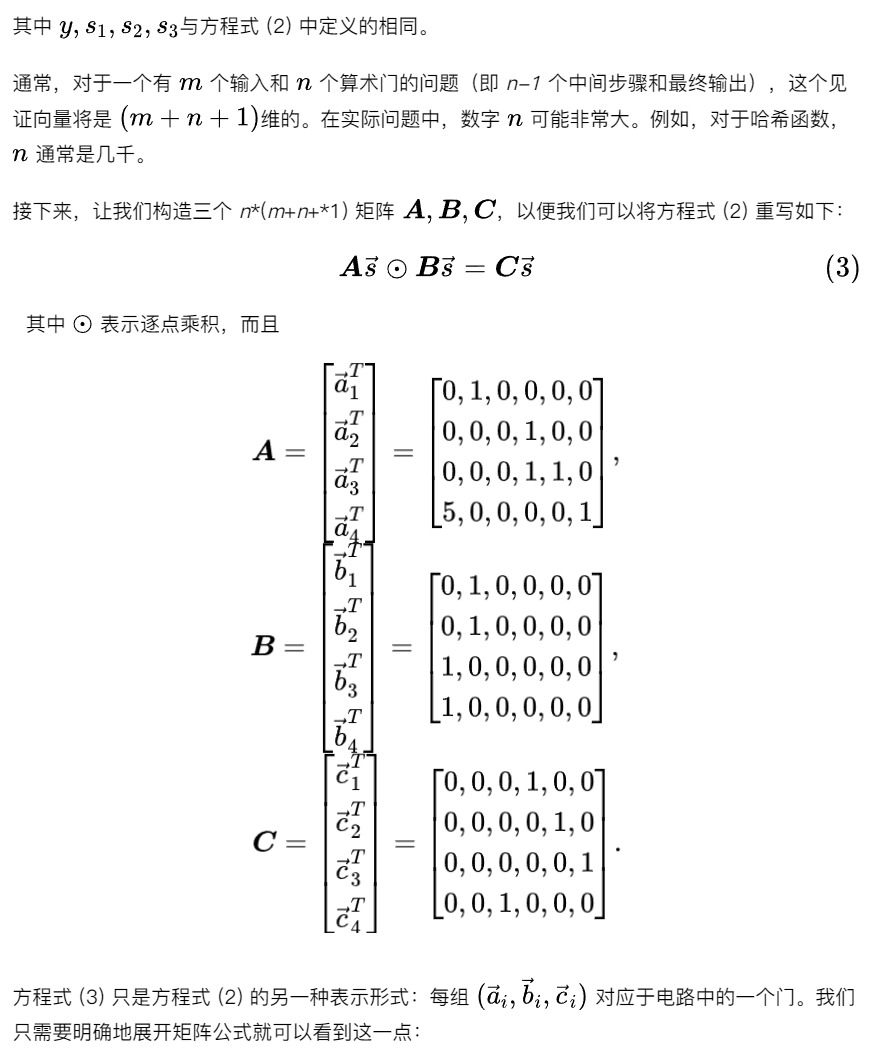
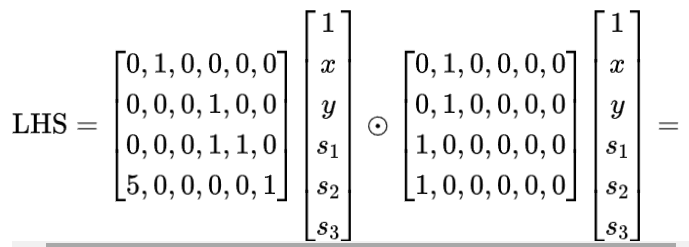
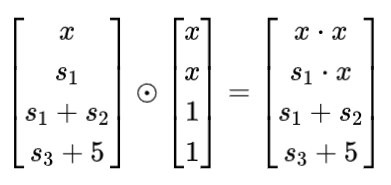

Step 3: Polynomial

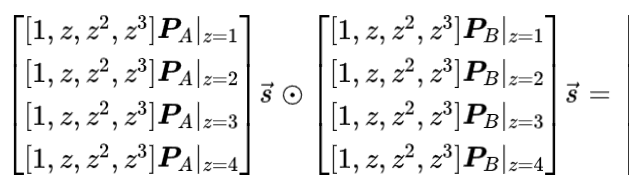
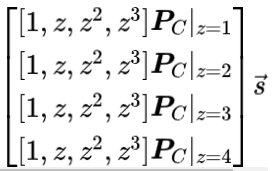
If you extract each row and observe it individually, it is not difficult to find that these four rows correspond to the same expression evaluated at four points. Therefore, the above matrix equation is equivalent to:

A straightforward but non-confidential way to prove this is to provide the left-hand side of equation (4) and show the factorization. However, the main purpose of zk-SNARK is to remain stealthy (not reveal any knowledge). Therefore, we will not prove this equation directly, but an encrypted version of it in the space of elliptic curve points.
Step 4: Elliptic Curve Points
Rewrite equation (4) as:

Next, we'll explain the actual steps in more detail.
Elliptic curve encryption

On the other hand, the addition of two elliptic curve points is defined as shown below:
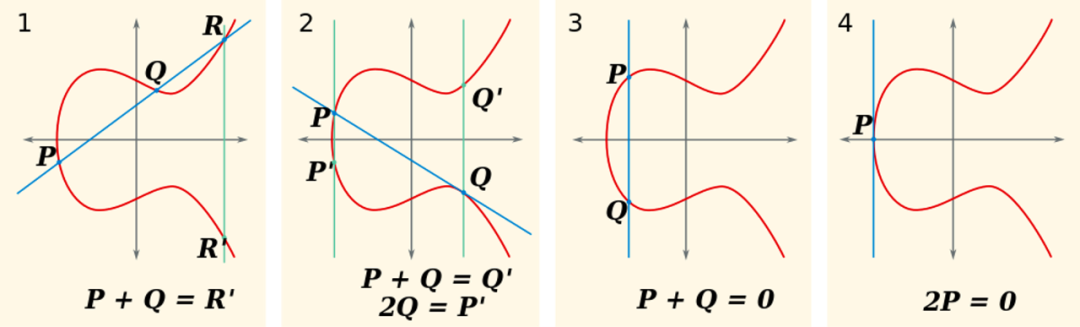


However, equation (5) that Alice wants to prove is in quadratic form, so it is not linear enough. In order to handle quadratic terms, we need to define multiplication in the encrypted space. This is called a pairing function , or bilinear map , and is explained next.
bilinear mapping

This is something we are all familiar with - the distributive law of addition and multiplication operations.
With such a bilinear mapping, we can map both sides of equation (5) to the encryption space.
public reference string

The entire process is called "Verification Key", or VK for short. Only 7 elliptic curve points (ECPs) are involved here, which need to be provided to the verifier. It should be noted that no matter how many inputs and first-level constraints are involved in the problem, VK is always composed of 7 ECPs.
In addition, it is worth mentioning that the "trusted settings" and the process of generating PK and VK only need to be done once for a specific problem.
Proof and Verification
Now possessing the public key (PK), Alice will calculate the following elliptic curve points (ECPs):
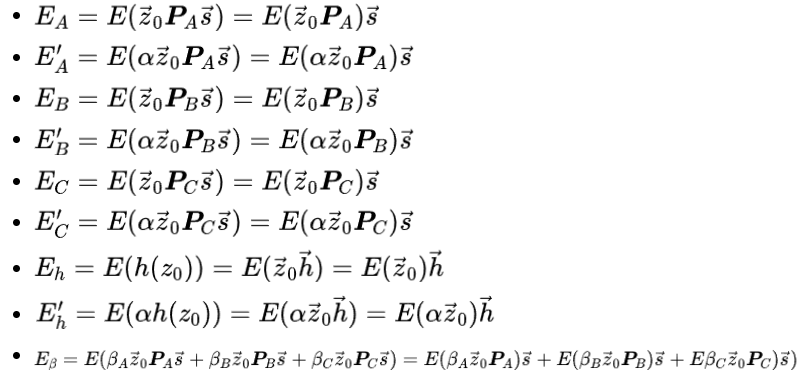
These 9 elliptic curve points are the key to zero-knowledge succinct non-interactive proof (zk-SNARK)!
Note that Alice actually just did some linear combination operations on the elliptic curve points in the public key. This is particularly critical and will be checked during verification.
Now, Alice has handed over the zk-SNARK certificate, and we finally enter the verification process, which is divided into three steps.

references
- “Zk-SNARKs: Under the Hood” (Vitalik Buterin)
- “A Review of Zero Knowledge Proofs” (Thomas Chen, Abby Lu, Jern Kunpittaya, and Alan Luo)
- “Why and How zk-SNARK Works: Definitive Explanation” (Maksym Petkus)
- Website: Zero-Knowledge Proofs
- Wikipedia: Elliptic curve
- Wikipedia: Finite field
- Wikipedia: Pairing-based cryptography
Disclaimer
The information in this research report comes from publicly disclosed materials, and the opinions expressed in this article are for research purposes only and do not represent any investment opinions. The opinions and forecasts issued in the report are only the analysis and judgment on the date of issuance and do not have permanent validity.
Disclaimer: As a blockchain information platform, the articles published on this site only represent the personal opinions of the author and guests, and have nothing to do with the position of Web3Caff. The content of this article is for information sharing only and does not constitute any investment advice or offer. Please comply with the relevant laws and regulations of the country or region where you are located.







