Institution: KuCoin
1 Introduction
Many cryptocurrency exchanges have adopted complex risk management measures to prevent liquidation risk. These measures include setting multi-tiered risk limits and restricting the use of high leverage. Furthermore, exchanges dynamically adjust parameters such as risk limits and margin ratios based on the prices of underlying assets and market liquidity. However, these processes are not only complex but also lack clear management standards, requiring a significant amount of resources to maintain a potentially inconsistent system - for example, increasing funds does not necessarily lead to a larger position size, as the leverage level may change abruptly.
On some trading platforms (see Figure 1), there are nearly a hundred risk limit levels. These passive level changes increase the complexity of system management and may result in partial forced liquidations, thereby harming user interests.
Our goal is to develop a non-linear model to simulate the reasonable position size under a given capital, thereby achieving more flexible and efficient risk management. This approach involves restructuring the internal formula system to achieve self-consistency, providing a feasible alternative to the existing complex risk limit templates.
This paper proposes a new risk management framework to replace the existing limit models. This method has been implemented in KuCoin's cross margin system, exhibiting some obvious advantages:
1. It is closer to the position management settings of traditional exchanges, making it easier for institutional capital to adapt.
2. It does not require adjusting risk limits based on position size or leverage usage.
3. It simplifies the operational process, reducing the burden on the exchange and lowering the risk of harming user interests to protect the exchange's own interests.
This model provides a more transparent and simplified way of risk management, aligning the exchange's operations with user interests.
2 Model
2.1 Maximum Position Size
Assuming the user's account holds a capital of C, and the futures contract price of the underlying asset is p. The initial margin rate r corresponds to the reciprocal of the user's chosen leverage. Ignoring transaction fees, the number of contracts the user can open is:

However, when the capital C is too large or the margin rate r is too low, the risk to the exchange will increase significantly. Therefore, when C and r are fixed and C is large, the exchange's risk grading system will limit the maximum allowed position, which is usually far lower than C/(p*r). Conversely, for smaller capital C, the position size is closer to C/(p*r).
Many exchanges use dozens to hundreds of risk levels to manage this relationship. As a result, users often need to adjust their risk level as their capital grows. The purpose of such restrictions can be roughly expressed by the following logarithmic function:
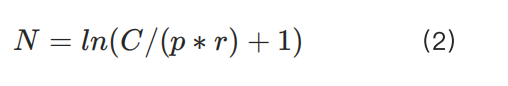
Clearly, when C is large, the first-order derivative of the logarithmic function decreases, meaning that the achievable position size will be less than the result calculated by the linear formula. However, this poses a challenge: for the approximation ln (x+1)≈x to hold, C must be small enough, and p must be large enough. Otherwise, even if C is small, the user may still be unable to achieve the theoretical maximum position of C/(p*r).
To solve this problem, we need to introduce a larger scaling parameter k based on the characteristics of different contract types, modifying the original formula to:
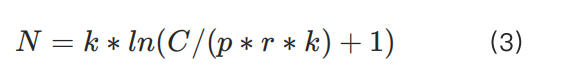
This adjustment meets the needs of small-capital users while also satisfying the risk control requirements of large-capital users.
In KuCoin's cross margin system, considering the existing positions and other margin requirements, we define the following variables:
•F: The margin occupied by other contracts and pending orders.
•E: The total equity in the user's futures account.
•Q: The position size of pending orders in the same direction as the new order.
•O: The current position size (positive if in the same direction as the new order, negative if in the opposite direction).
The formula for calculating the maximum allowed position is:
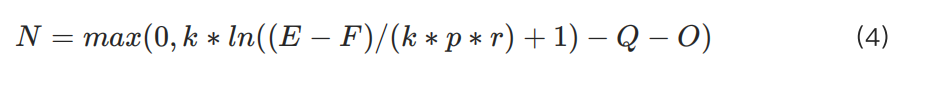
Therefore, in KuCoin's model, the relationship between leverage and maximum allowed position for typical capital sizes can be represented as follows:
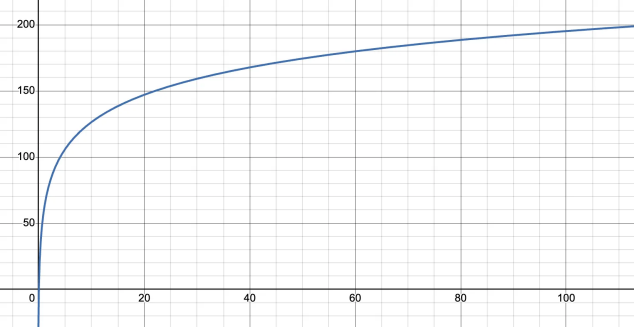
This chart shows how the model, with the help of non-linear margin adjustments, achieves a balance between scale and stability, satisfying the demand of small-capital users to maximize their positions while also ensuring risk control for large-capital users.
However, on most exchanges (such as OKX and Binance), the relationship between leverage and position size is often represented by a distorted curve:
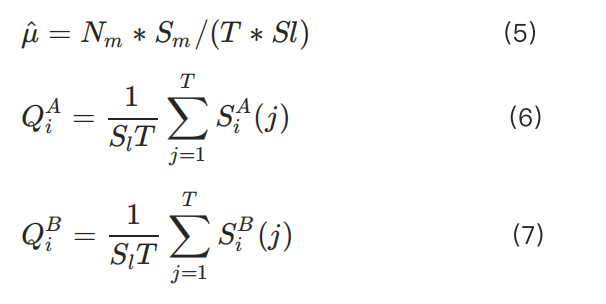
In fact, even the Maintenance Margin Ratio (MMR) exhibits a similar pattern. This is particularly challenging for large-capital users. For example, when the Initial Margin Ratio (IMR) is set to 50%, the MMR may reach as high as 48%. In this case, users attempting to open large positions are restricted to using low leverage, but the MMR increases to an unreasonable degree.
This setup limits the user's ability to effectively utilize their capital, as the abrupt changes in leverage levels require frequent adjustments, reducing flexibility. This creates an imbalance between risk management and user experience, making it difficult for large-scale investors to operate efficiently under these constraints.
2.2 MMR and IMR
The Maintenance Margin Ratio (MMR) is primarily used to help exchanges manage liquidation risk as a compensation mechanism. Essentially, the MMR reflects the pressure of liquidity extraction and needs to be dynamically adjusted as the open positions change. The following is the theoretical MMR derived based on the liquidity-related indicators that can be obtained by the exchange.
2.2.1 Liquidity-related Variables
To accurately assess liquidity, the following variables, which are typically visible to the exchange, have been identified:
•μ: The execution speed of market orders
•T: The time required for liquidation or exchange processing
•i: The distance from the best bid or ask price (price level)
•j: The time unit of the quote
•Qi: The average quantity of orders at a distance of i from the order book
•S: The average size of orders (represented by Sm for market orders and Sl for limit orders)
•N: The number of orders (represented by Nm for market orders, Nc for cancellations, and Nl for limit orders)
These values represent the average conditions in a stable market.
2.2.2 User Position Metrics Definition
• position: The instantaneous average position size of all users, which can be obtained from the exchange's historical data.
• pos: The position size held by any single user.
• X: The sum of trading volume during the MMR period.
• MMRup: The upper limit of the MMR.
• rMMR: The final value of the MMR.
• R: The actual distance from the best bid or ask price, which typically depends on i and j, and is different from r.
2.2.3 Adjusting MMR Based on Order Flow
The entry and withdrawal speeds of limit orders are incorporated into the average values across multiple levels. Since market orders are more likely to be executed immediately, their relative increases or decreases need to be considered. The following relationship defines this dynamic change:
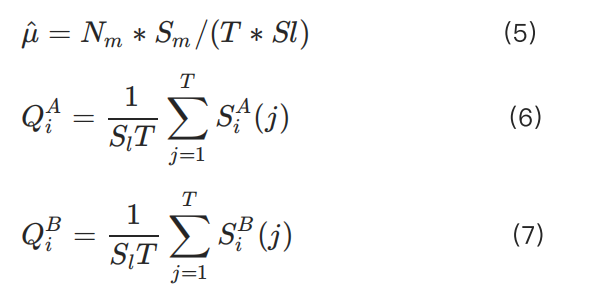
For example, for long positions, the strong liquidation liquidity can be the quantity of buy orders (Q):
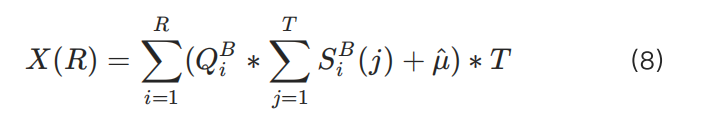
To ensure the exchange's safety, the following formula is derived:

Here, we can see that the position and R have an approximate inverse relationship. For the minimum order quantity:

Given the position, the constraint relationships of the variables make the MMR independent of p, so:
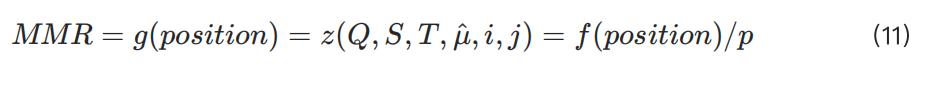
The final rMMR value can be expressed as:
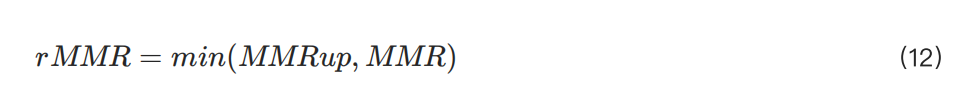
From the above equation, it can be seen that except for R, the other variables such as position, Q, S, and T have been determined. Therefore, they can be derived from these variables and then MMR and rMMR can be calculated.
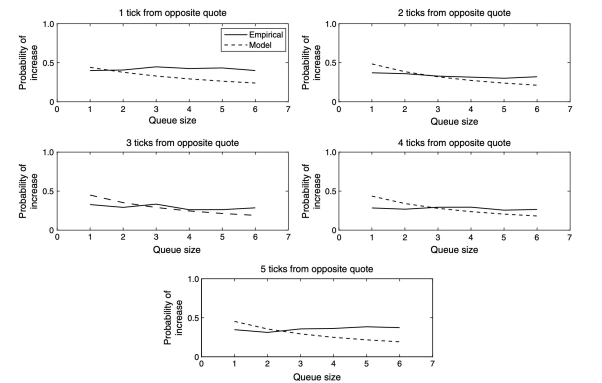
In addition, it is necessary to set an upper limit for MMRup, because the model tends to be conservative and ignores the positive impact of key price levels and important order book levels on the order book. Some research from CME (see Figure 2) more accurately shows this impact.
The IMR (initial margin rate) is usually related to the leverage and liquidity of the underlying asset, so it often needs to be dynamically adjusted based on factors such as position size. It can be defined as:
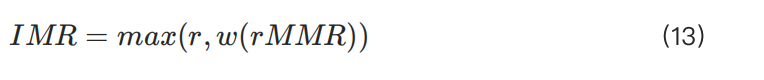
Here, IMR corresponds to the initial margin rate r mentioned in Section 2.1. The function w(rMMR) provides greater flexibility. For example, if the exchange believes its liquidity is relatively stable, a simple adjustment can be used, such as: w(rMMR)=1.3×rMMR.
This method provides a practical way to dynamically adjust the margin rate, ensuring that IMR reflects the current market conditions and liquidity level. Compared to fixed margin rules, this makes the system more adaptive and benefits both users and the exchange through effective risk management.
3 Approximate solution k
The parameter k is a global parameter set for each specific asset (trading pair) and does not need to consider existing orders or open positions. In principle, the larger the value of k, the more positions the user can open. However, there is a key constraint here: the margin required for the maximum allowed position cannot exceed the total capital multiplied by the value of IMR.
For simplification, we will assign the formula for the maximum allowed position to the variable :
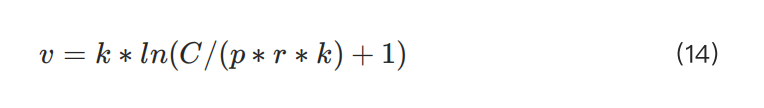
The actual leverage must be less than or equal to the reciprocal of the used margin:
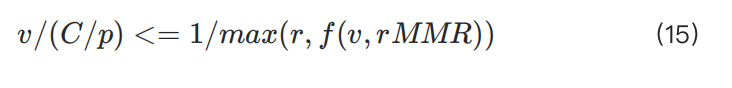
Introduce a new variable y to replace C (capital) and p (price) to simplify the calculation:

Obtain:
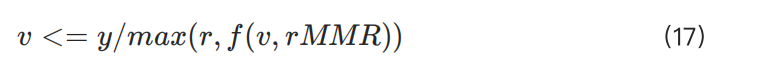
Except for very small positions, the simplified adjustment 1.3 × rMMR (using f(pos,rMMR)) is usually less than r. For smaller positions, the required margin becomes negligible, so such scenarios are not considered in our risk model. Similarly, MMRup sets an upper limit, which can also be ignored in this context.
Therefore, we only need to consider the minimum possible value of 1/IMR. This inequality can thus be simplified to:
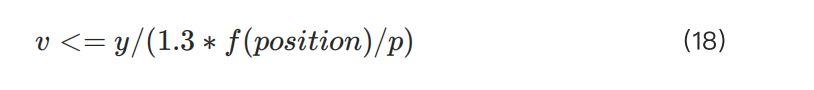
This inequality shows the relationship between the maximum allowed position and the actual leverage.
Unlike other variables, position and R have a clear inverse relationship. Therefore, the MMR derived from R can also be inversely proportional to the position and can be expressed as:

Assuming that under low position conditions, MMR follows the traditional form (half the reciprocal of leverage), the formula can be written as:
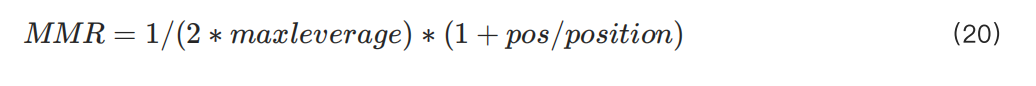
In this case, if we try to find the limit value of k, the r in formula (3) will become 1/maxleverage.
After substituting the variables, inequality (18) can be transformed into:
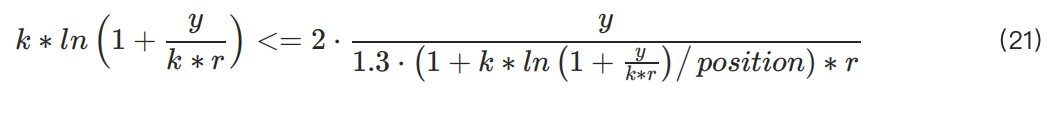
We observe that y (determined by the user's capital) should not theoretically affect the value of k. Therefore, k mainly depends on the position. Although the minimum value of k will vary with y, the goal is to find the minimum possible value under all conditions to ensure the safety of opening positions in any scenario.
Here, y/(k*r) can still be replaced by a variable, but the equation is still complex and difficult to solve analytically. After extensive approximate experiments and iterative simulations, it was found that k converges to a very simple expression (but the calculation of k is quite complex, and no detailed explanation is given here):
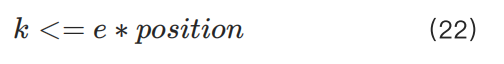
By adjusting the value of k or the position, users can open positions up to C/(p*r) when the capital amount or the number of open positions is not large. Otherwise, they will be restricted. The scale and degree of restriction are jointly controlled by k and the position. Therefore, different cryptocurrencies often correspond to different k values.
4 Conclusion
The above is a brief introduction to the cross margin risk limit system of Kucoin. The advantages of this design and its user-friendliness are evident. In Kucoin's cross margin system, in addition to risk limits, other elements such as risk ratios and the use of order margins are also dynamically managed through the mark price. This dynamic management not only maximizes the release of user margin, but also seamlessly integrates with the new risk limit framework, thereby improving system efficiency and user experience.
5 Appendix
Figure 1:
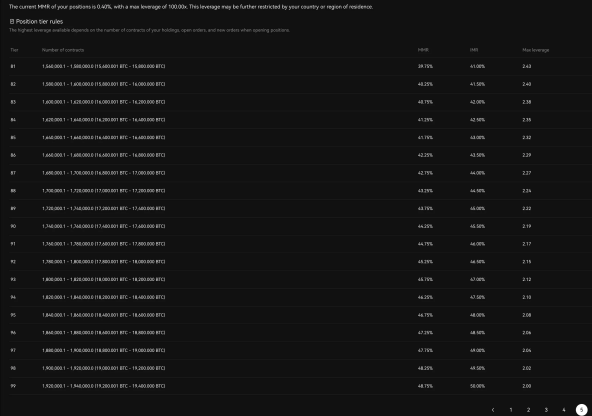
Figure 2:
6 References
1. Rama Cont, Sasha Stoikov and Rishi Talreja, "A Stochastic Model for Order Book Dynamics", Operations Research, 2010, Vol. 58, No. 3, pp. 549–563.
2. "Forecasting Initial Margin Requirements — A Model Evaluation", Journal of Financial Markets, Vol. 40, 2018.
3. Alfonsi, A., A. Schied, A. Schulz, "Optimal execution strategies in limit order books with general shape functions", Quant. Finance, 2010, Vol. 10, No. 2, pp. 143–157.