Understanding Silent Payments (Part 2)

Author: benma & Sebastian

Source: https://blog.bitbox.swiss/en/understanding-silent-payments-part-two/

See previous part here

In the previous article, we learned the technical foundations of silent payments. Now, let's take a closer look at how silent payments work in hardware signers (like BitBox).

We highly recommend reading the previous article in this series, as this article builds upon the knowledge discussed in the previous one, specifically the properties of private and public keys and how silent payments work. Like the previous article, we will use lowercase letters to represent private keys and uppercase letters to represent public keys. For example: A = a × G .

To recap, when Alice wants to send a silent payment to Bob, the transaction output arranged for Bob is dynamically derived from Bob's silent payment address and Alice's private key:

P = B_spend + hash(input_hash × S) × G

Where S is the shared secret value between Alice and Bob. Alice's hardware signer can calculate it using her own private key a and Bob's public key B_scan:

S = a x B_scan

Here, the B_spend and B_scan used by Alice are obtained from Bob's silent payment address, and a is the sum of private keys of all inputs in this transaction.

Creating and Signing Transactions

The first thing we need to understand is that silent payments greatly change the role of hardware signers when processing Bitcoin transactions.

In previous payment forms, the host wallet (software on your computer or phone, like BitBoxApp) creates the transaction, and the hardware signer (like your BitBox02) only verifies and signs it (provides permission).

In silent payments, things are different. The hardware signer is not only responsible for signing but also for generating part of the transaction, specifically the transaction output for Bob. This is because generating the transaction output for Bob requires Alice's private key, which only her hardware signer knows.

This paradigm shift brings some new risks:

• Memory Corruption: If the hardware signer has a bug or memory failure, it might derive an incorrect output, sending funds to an unspendable address, effectively losing the money.
• Malicious Behavior: If the hardware signer is tampered with, it could create an output directly sending funds to the attacker (instead of Bob) without the host wallet noticing.

This issue can be elegantly solved by having the host wallet verify the correctness of the silent payment output generated by the hardware signer. This is conceptually similar to "anti-klepto" - another case where the host wallet verifies that the hardware signer is not acting maliciously.

Discrete Logarithm Equality Proof

So, how does the host wallet verify that the silent payment output generated by the hardware signer is correct?

The host wallet can't directly verify it because it cannot regenerate the silent payment output. This would require either Alice's private key a or Bob's private key b_scan to calculate the shared secret value S, neither of which the host wallet can obtain.

Instead, we use a cryptographic tool called "Discrete Logarithm Equality (DLEQ) Proof" to allow the host wallet to verify the silent payment output generated by the hardware signer.

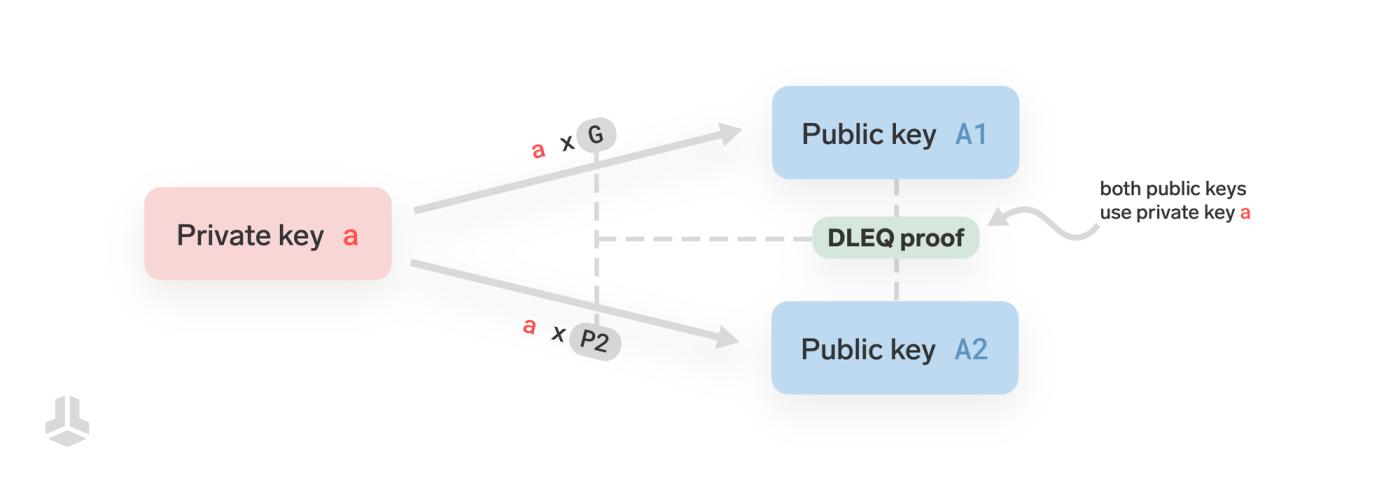
A discrete logarithm equality proof allows you to prove that the same private key a was used to generate two different public keys, although these public keys were generated through different "starting points" (also called "base points").

The first public key is A1 = a x G, where G is the commonly used base point (generator). The second public key is A2 = a x P2, where P2 is another base point. The proof guarantees that both public keys come from the same private key a, without revealing the private key itself to the verifier.

In simple terms, you're proving that although these two public keys were generated using different base points (G and P2), they both used the same secret value (private key a).

In technical terms, this proof demonstrates that the discrete logarithm of public key A1 with respect to base G is the same as the discrete logarithm of A2 with respect to base P2.

Verifying Correctness

The protocol that allows the host wallet to verify the correctness of the silent payment output is as follows:

The hardware signer creates the silent payment output and a DLEQ proof, proving that the secret value in the public key A = a x G and the shared secret value S = a x B_scan is the same (private key a).

• Because A and S are both derived from the same private key a, the DLEQ proof guarantees that the public key secret value S is also generated using Alice's private key.

The hardware signer sends the generated payment output P, the shared secret value S, and the DLEQ proof to the host wallet.

The host wallet uses the following three elements to verify the DLEQ proof:

1. Public key A, which is the sum of public keys of all inputs in Alice's transaction;
2. B_scan from the silent payment address, and
3. S, provided by the hardware signer

• If the proof passes verification, the host wallet can be confident that S was correctly calculated as a x B_scan, even though the host wallet doesn't know the private key a.

Now, the host wallet can independently verify the silent payment output by recalculating:

P = B_spend + hash(input_hash × S) × G

To do this, the host wallet needs to extract B_spend from Bob's silent payment address, independently calculate input_hash from the transaction inputs, and obtain S from the hardware signer (which was verified in the previous step).

• If the recalculated silent payment output matches the output returned by the hardware signer, the host wallet can safely finalize and broadcast the transaction, as it knows that the silent payment output is correct and has not been tampered with.

Process Summary

• Alice's hardware signer creates a silent payment output and uses a DLEQ proof to demonstrate that it is using the correct private key.
• The host wallet verifies the proof to ensure that the shared secret value is correctly calculated.
• The host wallet recalculates and verifies the silent payment output using the shared secret value and known outputs from the transaction; if all checks pass, it finalizes the transaction.

This method characterizes that the hardware signer cannot manipulate anything, whether due to hardware damage or malicious activity.

Launch

The features ensuring the security of silent payments, including implementing the correctness checks described in this article in BitBoxApp, will be released in BitBoxApp version 4.45 and BitBox firmware version 9.21.

BitBox02 is the first hardware signer to support sending silent payments. If the broader ecosystem does not support sending silent payments, it would be difficult to convince other wallet software, exchanges, service providers, etc., to add support for silent payments. This is a chicken-and-egg problem. We hope we can help promote the adoption of silent payments in this way.

Thanks to Open Source Collaboration

We first heard about silent payments at the 2023 BTC Azores unconference, from the talks by BIP authors josibake and Ruben Somsen. The BIP itself received many high-quality reviews.

When we started drafting the implementation for BitBox02, I began thinking about the risks mentioned above and posted a tweet listing my concerns. Josie, Ruben, and Andrew Toth kindly pointed out that DLEQ proof is a possible solution and provided me with some very useful reading material. The only missing piece was a high-quality, reviewed DLEQ implementation.

When Andrew Toth began writing a detailed BIP draft describing DLEQ, cryptographer Tim Ruffing recalled that an implementation already existed in the secp256k1-zkp library, which BitBox02 was already dependent on. This was provided by jesseposner for another use case, but fortunately, this implementation proved to be very suitable for silent payments.

With the help of the test interface from the BIP, the above DLEQ implementation, and a useful reference implementation (although we could not directly use this reference implementation due to different requirements for hardware signers), we were able to smoothly integrate support for silent payments into BitBox.

It is always exciting when so many people voluntarily contribute their time and effort to build something in an open environment and ultimately succeed in gathering small contributions to create something significant.

Heartfelt thanks to Josie, Ruben, Andrew, and many others who helped us complete this feature.