Abstract
We want to motivate the usage of rateless codes, particularly Random Linear Network Coding (RLNC) through an on demand sampling approach instead of sampling from a fixed coded set as done in prevailing DAS methods like Celestia, SPAR, or Peer/Full DAS from the perspective of sampling efficiency.
Why Fixed Rate Codes?
The original motivation for the usage of coding for DAS was that, under anonymity, sampling from uncoded data only decreases false negative probability (a verifier concluding that data is available even though it is not) linearly with the number of samples taken as 1 - s/k for s samples taken from k uncoded chunks. Now, if we apply a (n,k) RS code for example, the false negative probability for s samplings (without replacement) decreases faster than (k-1/n)^s
Increased Sampling Efficiency Through Rateless Coding
By employing fixed rate coding, the verifier (light client) inherently restricts itself to sampling from a pre-coded set of n symbols. Looking at the false negative probability above for sampling from fixed rate coded data, the question that naturally arises is: why not make the n as large as possible so that the false negative probability is sufficiently low even for a small number of samples? There are several downsides to this including:
The codes used here are usually codes like RS codes that have inherent limits on the magnitude of
nas well as the possible combinations of(n,k).storage and computational cost at the data producer would inadvertently increase alongside bandwidth costs for dispersal of sampling data to custody nodes like for example in PeerDAS.
A natural solution to this problem would be to create samples on demand to prevent the storage and dispersal bottlenecks, which naturally leads us to consider rateless codes as those can be viewed as maximum distance separable (MDS) codes in the limit for large n. RLNC is one example of such a rateless code that builds coded packages by forming random linear combinations of the original data.
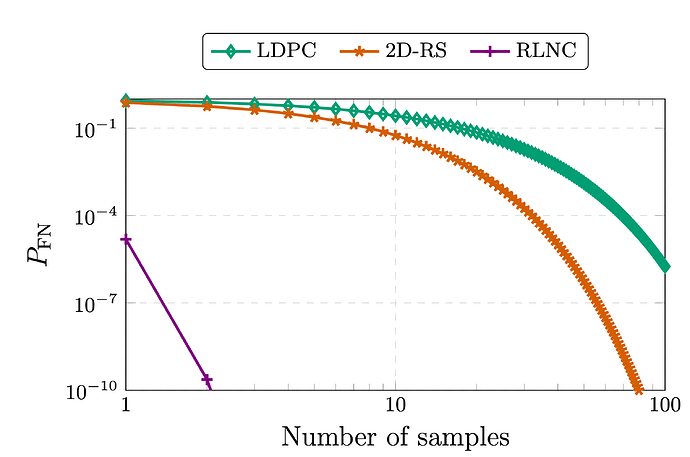
On demand sampling from a code like RLNC provides a false negative probability of (1/q)^s where q denotes the cardinality of the field for the coding coefficients. The full description of one such protocol is given in this paper: From Indexing to Coding: A New Paradigm for Data Availability Samping
Probability of a false negative (Undecodability of the underlying payload is not detected) for sampling from coded data (see [1],[2]).
Potential for true Decentralisation
Another downside with fixed rate coded data is that samples are individualized which gives room for expensive repairability procedures. For 1D RS codes, as used in PeerDAS for example, losing a single Cell of an RS coded blob requires downloading the equivalent of an entire blob to reconstruct the data due to the bad locality properties of RS codes. Once tensor codes are introduced this will get better but an unstructured code like RLNC can also provide a more decentralized version of distributed custody,
A protocol for decentralized custody using RLNC has been proposed by @Nashatyrev showing favorable properties in repair bandwidth as well as dissemination and storage overhead.
References
[1] Al-Bassam, Mustafa, et al. “Fraud and data availability proofs: Detecting invalid blocks in light clients.” International Conference on Financial Cryptography and Data Security. Berlin, Heidelberg: Springer Berlin Heidelberg, 2021.
[2] Yu, Mingchao, et al. “Coded merkle tree: Solving data availability attacks in blockchains.” International Conference on Financial Cryptography and Data Security. Cham: Springer International Publishing, 2020.