도플러에 대해 알아보세요 - 네덜란드 경매와 본딩을 결합한 토큰 배포 프로토콜...

Coin68

03-16

이 기사는 기계로 번역되었습니다

원문 표시

도플러 프로토콜의 운영 모델의 핵심은 더치 경매 동적 본딩 곡선입니다. 이는 더치 경매 모델과 기존 본딩 곡선을 원활하게 결합하여 보다 공정한 토큰 배포 모델을 제공합니다.

Doppler에 대해 알아보기 - 네덜란드 경매와 본딩 커브를 결합한 토큰 배포 프로토콜

소개

AMM(자동 시장 조작자) 모델의 개발은 DeFi 붐을 일으켰고, 블록체인 분야에서 디지털 자산에 대한 시장이 생성되는 방식을 완전히 바꾸어 놓았습니다.

중앙화된 거래소에 의존하고 주문장 모델을 사용하여 주문이 매칭될 때까지 기다리는 대신, AMM은 제3자의 개입이나 신뢰가 필요 없이 수학 공식을 사용하여 거래를 자동으로 실행합니다.

또한 허가가 필요 없고 신뢰할 수 없는 특성 때문에 수백만 개의 암호 자산이 수년간 이 모델로 운영되어 왔습니다. 특히 지난해에는 많은 네트워크에서 "펌프펀 운동"이 일어났습니다.

AMM의 일반적인 공식

그러나 AMM 모델은 여전히 상당한 과제에 직면해 있습니다. 첫째, 이 모델은 시장을 창출하기 위한 초기 자본이 필요합니다.

알다시피 창작자는 양방향 유동성을 제공해야 합니다. 프로젝트에는 자체적으로 인쇄한 토큰 외에도 ETH, USDT, USDC 또는 네트워크에 따라 다른 기본 토큰과 같이 인정된 가치가 있는 상당량의 플랫폼 토큰이 필요합니다. 이는 재정적 잠재력이 제한적인 개발자에게 장벽이 될 수 있습니다.

Uniswap v3의 CLMM 이나 Meteora 의 DLMM과 같은 AMM의 이후 버전은 단방향 유동성을 허용하지만, 여전히 메이커가 시작 가격에 대한 견해를 가져야 하거나, 달리 말해 프로젝트 스스로 가격을 책정해야 합니다.

이는 프로젝트와 사용자 모두에게 초기 가격 발견 문제라는 다음 과제를 안겨줍니다.

가격이 너무 높으면 사용자가 거래를 거부하여 상장이 실패하게 됩니다. 토큰 가격이 너무 낮으면 저격 봇에 의해 악용될 수 있습니다. 저격 봇은 낮은 가격에 즉시 매수하여 나중에 매수할 사람에게 높은 가격에 재판매하므로 프로젝트에 불필요한 손실이 발생합니다.

제품과 프로젝트의 깊이에 관심이 있고 매수하여 장기간 보유하려는 투자자는 즉시 손실을 입지만, 분 단위로 단기 이익에만 관심이 있는 저격수 봇은 막대한 이익을 챙깁니다.

어떤 봇은 지난달 https://t.co/C909I8882s 에서 #memecoins를 공격하여 약 27,000 달러 (약 680만 달러)를 벌었을 수 있습니다!

2일 전, 이 봇은 2 달러 솔라나(SOL) 만을 사용해 5,700만달러의 FATHA를 저격한 후 이를 모두 4,456 달러 솔라나(SOL) 에 판매하여 4,454 달러 솔라나 (112만 달러)의 수익을 올렸습니다. 무려 2,227배의 수익이죠!

오늘은 1.75달러를 썼습니다… pic.twitter.com/BQf15VpClQ
— Lookonchain (@lookonchain) 2024년 11월 25일

최근의 펌프펀 운동은 본딩 커브 게임이 항상 봇의 손에 달려 있다는 사실을 보여줍니다. 실제 사용자는 경쟁할 수 없습니다. 심지어 본딩 커브에서 판매된 토큰을 모두 사들인 후, 다음 구매자에게 재빨리 덤핑하는 봇 프로젝트도 있습니다.

1분 만에 성장하는 차트, 1시간 만에 수억 원의 자본금을 늘리고 1분도 채 안 되어 수천 달러로 늘리는 러그풀과 같은 차트는 펌프펀에서 흔히 볼 수 있습니다. 조작팀은 봇을 이용해 아래의 모든 토큰을 매수해 시가총액을 올리기 때문에 아무도 더 낮은 포지션을 매수할 수 없습니다. 따라서 필요하다면 봇은 모든 토큰을 덤핑해 거래 수수료에서 아주 소액의 손실만 감수하면서 원금을 회복합니다.

게임의 공정성을 확보하기 위해서는 프로젝트의 초기 가치를 알아내는 것이 매우 중요합니다.

Pumpfun의 인기 있는 공급 제어 저격 차트 패턴

이러한 사실은 암호화폐 환경에 프로젝트와 투자자 모두에게 이익이 되는 공정한 토큰 배포 모델이 필요하다는 것을 보여줍니다.

Whetstone Research 의 개발자들은 다양한 잠재적 적용 분야를 지닌 더치 경매와 본딩 커브를 결합한 새로운 토큰 배포 모델을 도입했습니다. 다음 섹션에서는 더치 경매 동적 결합 곡선과 도플러 프로토콜에 대해 자세히 알아보겠습니다.

더치 경매 동적 결합 곡선 모델

도플러 프로토콜의 운영 모델의 핵심은 Dutch Auction Dynamic Bonding Curve로, Dutch Auction 모델과 전통적인 본딩 커브를 매끄럽게 결합한 것입니다. 먼저 이 두 모델을 살펴보겠습니다.

더치 옥션 - 더치 옥션

네덜란드식 경매는 내림가 경매라고도 하며 , 자산의 가격을 매우 높은 시작 가격으로 제시한 다음 시간이 지남에 따라 점차 낮아져서 누군가가 매수할 의향이 생길 때까지 진행되는 경매 형태입니다.

마찬가지로, 암호화폐 시장에서 더치 경매는 종종 미리 정해진 시간 동안 가격이 점차 낮아지는 스마트 계약을 통해 구현되며, 누군가가 가격을 수락할 의향이 있으면 거래가 실행됩니다.

더치 경매는 봇 조작과 MEV(Miner Extractable Value) 공격을 완전히 근절하는 것으로 입증되었습니다. 가격이 높은 것에서 낮은 것으로 점차 낮아지기 때문에 스나이퍼 봇을 사용하는 것은 전혀 의미가 없습니다. 이 게임은 "머리보다 손이 빠른" 사람을 위한 것이 아니라 프로젝트 가치 평가를 위한 조사용입니다. 참여자는 어느 구역에서 매수를 시작할지 스스로 결정해야 하며, 이를 통해 프로젝트의 초기 가치 평가 결정권은 창작자로부터 투자자에게 이전됩니다.

또한, 이런 식으로 토큰을 배포하면 창작자는 양방향 유동성을 제공할 필요가 없고, 투자자가 수용할 때까지 시간이 지남에 따라 가격이 하락하도록 두면 됩니다. 이 모델은 좋은 아이디어는 있으나 재정 자원이 부족한 프로젝트에 실제로 유용합니다.

본딩 커브

본딩 곡선 은 암호화폐 경제에 적용되는 수학적 모델로, 토큰 공급과 가격 간의 관계를 결정합니다. 이 공식은 스마트 계약을 통해 자동으로 정의되고 실행됩니다.

기본적으로 본딩 곡선의 공식은 P = f(S) 입니다. 여기서 P는 토큰 가격, S는 유통 공급량, f는 사용자 정의 계산 함수입니다. 동일한 토큰 유형에 대해서도 함수 f가 다를 수 있으며, 이로 인해 하위 곡선의 모양이 달라질 수 있습니다.

다양한 결합 곡선 모델의 예

채권곡선은 자산의 수요-공급 관계를 직접적으로 반영하는데, 수요가 증가하면 가격도 상승하고, 반대로 수요가 증가하면 가격도 상승합니다. 다시 말해 수요와 공급에 따라 가격이 연속적으로 결정됩니다. 이러한 증가나 감소는 수학적 공식을 통해 자동으로 결정되므로 제3자를 신뢰하지 않고도 시장의 지속적인 운영이 투명하게 보장됩니다.

본딩 커브는 인기를 끌고 있으며 수년 동안 토큰 배포 표준이 되었습니다. 대표적인 프로젝트로는 pump.fun , friend.tech , four.meme 등이 있습니다. 유니스왑 과 팬케이크스왑과 같은 분산형 거래소도 이러한 본딩 커브 모델을 기반으로 운영됩니다.

이는 서론에서 언급한 대로 많은 뛰어난 이점을 가져다주지만, 토큰 배포 활동에 적용하면 공정한 거래 환경을 구축하는 데 큰 어려움을 초래할 것입니다.

이로 인해 Whitestone Research의 개발자들은 네덜란드 경매와 채권 곡선 모델을 결합하는 방법을 생각해냈습니다. 이는 네덜란드 경매 동적 결합 곡선의 탄생을 위한 기반이 되었습니다.

더치 경매 동적 결합 곡선

더치 경매 동적 결합 곡선(DADBC)은 더치 경매와 결합 곡선을 매끄럽게 결합한 것입니다. 토큰 출시는 네덜란드 경매로 시작됩니다. 네덜란드 경매에서는 가격이 매우 높은 수준에서 하락하다가 투자자들이 수용할 만한 매수 구역을 찾은 후 동적 본딩 곡선이 가격 경로를 차지하기 시작합니다.

이 가격 곡선은 고정되어 있지 않고 시장의 수요와 공급에 따라 유연하게 변하기 때문에 '동적'이라는 키워드를 추가했습니다. 매수력이 너무 강하면 곡선이 위로 이동하여 가격이 상승합니다. 매수력이 너무 약하면 곡선이 아래로 이동하여 가격이 하락하여 매수력이 생길 수 있는 조건이 조성됩니다. 아래의 그림을 보세요.

구체적으로는 다음과 같습니다.

Dutch Auction Dynamic Bonding Curve는 Uniswap v3의 틱 메커니즘을 사용하여 가격 증가 및 감소를 실행합니다.

모르시는 분들을 위해 말씀드리자면, Uniswap은 버전 3부터 "틱"을 사용하여 가격을 개별적인 작은 수준으로 분할하여 중앙 집중형 유동성 모델(CLMM)을 제공합니다. 각 틱은 다음 공식에 의해 결정되는 가격의 작은 단계 변화입니다. 가격=1.0001 ^틱 . 틱 기반 가격 세분화는 CLMM 모델에서 유동성 공급 효율성을 높이는 데 도움이 됩니다.

일반적으로 복잡한 상황을 피하기 위해서는 Dutch Auction Dynamic Bonding Curve의 가격 상승 및 하락이 임의의 숫자가 아닌 틱 단위로 움직인다는 점을 이해하면 됩니다.

위 차트는 네덜란드 경매 중에 가격이 지정된 기간 내에 지정된 최대 틱에서 최소 틱으로 낮아짐을 보여줍니다. 각 감소 단계의 시간 단위는 1시대입니다.

수요 구역이 발견될 때까지 가격은 각 시대마다 계속 하락하며, 그런 다음 동적 결합 곡선이 적용됩니다.

이제 동적 결합 곡선 단계에 들어갑니다. 동적 결합 곡선이 어떻게 작동하는지 이해하려면 다음과 같이 모델에서 곡선을 계산하는 공식을 알아야 합니다.

동적 결합 곡선 결정 공식

거기에는:

bc(t): 시점 t에서의 채권 곡선 값으로, 해당 시점의 자산 가격을 계산하는 데 사용됩니다. 𝑝(𝑡) = 1.0001𝑏𝑐 (𝑡).
γ: 결합 곡선의 기울기를 결정하는 매개변수.
tmax: 총 토큰 판매 시간.
τt: 원점 틱, 시간 t에서의 결합 곡선의 원점 또는 시작점.

따라서 기울기와 시간 외에 우리가 주목해야 할 중요한 매개변수는 τt(원점 눈금) 입니다. 곡선이 시작하는 지점이 바로 동적 결합 곡선의 동적 메커니즘에서 핵심 지점입니다.

τt(원점 틱)는 시점 t에서 채권 곡선이 위로 이동하는지 아래로 이동하는지 여부를 결정하며, 이를 통해 시장 수요에 맞춰 매수 및 매도 가격을 조정합니다.

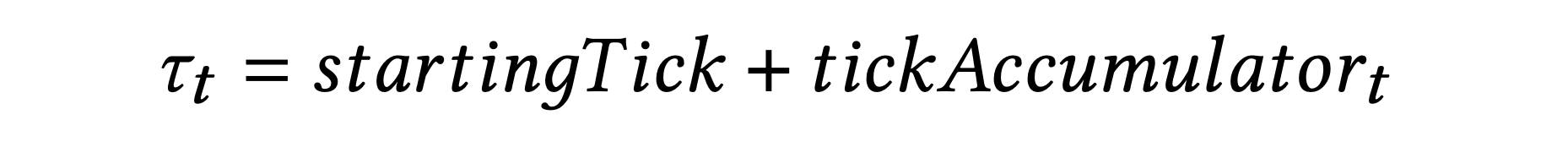
τt는 위의 공식에 의해 결정됩니다. 거기에는:

startingTick: 시작 틱은 처음부터 정의된 정적 매개변수입니다.
tickAccumulator(t): 본딩 곡선의 연속 조정 중 누적 틱입니다.

tickAccumulator(t) 는 tickDelta의 누적 합계입니다.

tickDelta는 곡선을 조정할 때마다 틱 값이 변경되는 양을 나타내는 매개변수입니다. 이는 3가지 경우에 결정됩니다.

위의 공식에는 새로운 변수가 있습니다.

λt : 에포크 t에서 판매될 것으로 예상되는 토큰 수.
𝜆𝑡^ : 에포크 t에서 판매된 실제 토큰 수.

3가지 경우가 있습니다:

If: 𝜆𝑡^ ≤ 0, 즉 실제로 판매된 토큰의 수가 0보다 작은 경우 => tickDelta가 maxDelta에 할당됩니다.
만약: 0 < 𝜆𝑡^ < λt이면, 실제로 판매된 토큰의 수는 0보다 크지만 예상보다 적은 것을 의미합니다 => tickDelta는 다음 공식에 의해 결정됩니다: maxDelta*(𝜆𝑡^/λt).
만약 𝜆𝑡^ ≥ λt라면, 즉 판매된 토큰의 수가 예상보다 많은 경우 tickDelta는 다음 공식에 의해 결정됩니다: tickDeltau,t.
maxDelta는 아래 공식에 의해 결정됩니다.

매도가 예상보다 클 경우 tickDelta _u,t를 계산하는 공식은 유동성 풀의 현재 틱 위치인 매개변수 i(c)와 결합해야 하기 때문에 약간 더 복잡합니다.

따라서 요약하면, 토큰 출시 캠페인을 여러 시대로 나누고 예상 판매량과 실제 판매량을 비교함으로써, 본딩 곡선은 시장 수요와 공급에 따라 지속적으로 조정되었습니다.

이 기간이 끝나면 모든 유동성은 마이그레이션이라는 이벤트를 거쳐 자유 거래로 전환됩니다.

복잡한 계산은 건너뛰고 무엇이 보이나요? 이 모델은 네덜란드 경매와 본딩 커브를 완벽하게 결합하여 새로운 토큰 배포에 대한 완전히 다른 접근 방식을 나타냅니다.

수요와 공급에 따른 지속적인 가격 조정을 통해 스나이퍼 봇 조작을 없애고 투자자에게 건전한 경쟁 환경을 조성합니다. 프로젝트 측면에서는 시장을 조성하기 위해 많은 양의 초기 유동성을 제공할 필요가 없습니다. 이 모델은 윈윈 모델로 볼 수 있습니다.

이러한 장점 외에도 Dutch Auction Dynamic Bonding Curve에는 몇 가지 한계가 있습니다. 예를 들어, 높은 가격에서 낮은 가격으로 역경매를 구현하면 대기 시간 측면에서 압박이 발생하고, 기회를 놓친다는 심리적 요인으로 인해 투자자가 원하는 것보다 높은 가격에 매수하기로 결정할 수 있습니다.

게다가, 더 이상 가격 포모 효과가 없기 때문에 이 방법은 프로젝트가 판매를 시작하기 전에 신뢰를 구축해야 합니다. 투자자들이 관심을 갖지 않으면 가격은 아무도 사지 않을 정도로 매우 낮은 수준까지 떨어질 수 있습니다.

마지막으로, 이 모델에 조작이 전혀 없다는 것은 아닙니다. 조작 집단이 의도적으로 높은 초기 매수 구역을 만들고 상승하기 시작하면 외부 투자자는 FOMO에 걸려 일찍 매수하기로 결정할 수 있습니다. 하지만 이 모델은 어차피 한계가 있을 것입니다. 투자자들이 자신의 가치 평가를 고수하고 매수를 거부한다면, 어느 순간 조작자들은 더 이상 높은 가치 평가에서 매수를 계속할 돈이 없게 될 것이고, 그러면 가격은 동적 채권 곡선의 조정에 따라 점차 하락할 것이고, 손실을 입는 것은 조작자들이 될 것입니다.

위에서 우리는 도플러 운영 모델의 가장 중요한 내용을 살펴보았고, 이어서 전체 프로토콜 모델의 아키텍처와 구성 요소에 대해 살펴보았습니다.

도플러 프로토콜

도플러는 EVM(이더리움 가상 머신) 생태계에서 토큰 배포와 유동성을 위해 네덜란드 경매 동적 본딩 곡선 모델을 사용하는 최초의 프로토콜입니다.

Doppler는 사용자가 토큰에서 유동성까지 프로젝트를 원활하게 배포할 수 있도록 하는 여러 구성 요소로 이루어진 모듈식 아키텍처로 설계되었습니다. 모듈형 아키텍처 덕분에 프로젝트에서 필요에 따라 개별 모듈을 쉽게 사용자 지정하고 조립할 수 있습니다.

도플러에는 토큰 팩토리, 유동성 팩토리, 마이그레이션 팩토리, 타임락 팩토리, 베스팅 모듈 등 5개의 주요 모듈이 있습니다. 이러한 모듈은 에어록이라는 중앙 모듈의 조정을 통해 작동됩니다.

Doppler에 배포된 토큰의 수명 주기는 다음과 같습니다.

토큰 생성: 토큰은 정의된 보안 표준을 적용하여 토큰 팩토리를 통해 새롭게 생성됩니다.
유동성 부트스트래핑: 네덜란드 경매 동적 결합 곡선을 사용하여 초기 유동성을 생성합니다.
AMM 마이그레이션: 시작된 유동성을 자동으로 기존 AMM으로 이체합니다.
유동성 보호: 필요한 경우 타임락 팩토리와 베스팅 모듈을 통해 유동성을 보호합니다.

토큰 팩토리

토큰 팩토리 는 사전 결정된 기준에 따라 토큰을 생성하는 모듈입니다. 이는 웹 3 공간에서는 사용자가 항상 사기 및 러그풀 위험에 직면하기 때문에 매우 중요합니다. 프로그래밍 지식이 없으면 일반 사용자가 토큰이 악성인지 아닌지 알아내는 것은 매우 어렵습니다. Doppler 토큰 팩토리에서 배포된 토큰은 인정된 보안 표준을 구축함으로써 사용자가 이러한 위험을 피하는 데 도움이 됩니다.

이는 솔라나 네트워크의 토큰이 펌프펀에서 발행되었는지 아닌지 확인할 때와 비슷합니다. 펌프펀에서 발행한 토큰이라면 판매 잠금, 높은 세금 또는 새로운 토큰 주조 가능성이 없을 것이라고 확신할 수 있습니다. 도플러 토큰 팩토리도 동일한 작업을 수행하지만 EVM에서 ERC-20 표준을 사용합니다.

유동성 공장

Liquidity Factory는 위에서 분석한 유동성을 창출하기 위해 Dutch Auction Dynamic Bonding Curve를 사용하는 모듈입니다. 토큰의 유동성을 시작하기 위해 공급과 수요에 따라 가격을 조정하고 초기 가격 구역을 찾는 역할을 담당합니다.

Liquidity Factory는 최근 업데이트의 후크 메커니즘 덕분에 Uniswap v4 위에 구축되었습니다. 하지만 해당 프로젝트에서는 Liquidity Factory가 Uniswap v3 및 기타 인기 있는 AMM과 호환된다고 언급합니다.

생성된 유동성의 양이 충분하다면 Airlock은 해당 작업을 마이그레이션 모듈로 전송하도록 조정합니다. 그 반대의 경우, Airlock은 참여 사용자에게 원금을 환불합니다.

이주 공장

마이그레이션 팩토리는 Liquidity Factory에서 AMM 프로토콜로 초기 초기화 단계 이후 유동성을 전송하는 작업을 수행하며, 이를 통해 토큰은 시장에서 자유롭게 거래될 수 있습니다.

타임락 팩토리

Timelock Factory는 상장 기간 이후 토큰 유동성을 보호하고 안정화하기 위해 타임락 계약을 만드는 데 중점을 둡니다. 자동 유동성 잠금 기능은 사용자가 갑작스러운 난항 상황을 피하는 데 도움이 됩니다.

베스팅 모듈

Vesting 모듈은 Vesting 일정에 따라 토큰 분배를 설정할 수 있는 모듈입니다. 이는 사용자를 청산 위험으로부터 보호하는 동시에 프로젝트 개발팀에 장기적인 동기를 부여합니다.

도플러 프로토콜은 공식 오픈소스 버전을 배포하였습니다. 자세한 내용 은 Github 주소를 참조하세요. 또한 이 프로젝트에서는 Pure.st 라는 Dutch Auction Dynamic Bonding Curve를 이용한 펌프펀 버전도 구축했습니다. 여기에서 체험해 보실 수 있습니다.

결론

도플러 와 더치 경매 동적 결합 곡선은 암호화폐 시장에서 주목할 만한 혁신으로, 특히 블록체인에서 저격 로봇이 맹위를 떨치는 상황에서 더욱 그렇습니다. 모든 참여자에게 더 공정한 환경을 조성하면 심각한 자본 흐름이 촉진될 것입니다.

도플러와 더치 경매 동적 결합 곡선은 장기적 비전을 갖춘 가치 지향적 프로젝트에 더 적합할 수 있습니다. 개발자는 이를 사용하여 자동 귀속을 통한 장기 참여 인센티브와 함께 공정한 유동성을 창출할 수 있습니다.

하지만 이 모델이 암호화폐 시장의 새로운 표준이 될지는 아직 불확실합니다. 혹독한 현실은 대부분의 암호화폐 프로젝트가 공급 통제, 가격 FOMO, 토큰 덤핑에 관한 것이라는 것입니다. 이런 식으로 수익을 창출하는 것은 제품 기능을 구축하는 것보다 수십만 배나 빠르고 쉬워서 장기적으로 잉여가치를 창출할 수 있습니다. 결과적으로 토큰은 프로젝트 자체에 의해 조작되는 경향이 있으므로 공정하고 투명한 토큰 배포 모델은 반드시 그들이 원하는 것이 아닙니다.