경제학에서는 "모호한 장치"가 다양한 유용하고 흥미로운 메커니즘 설계 특성을 가지고 있다는 것이 잘 알려져 있습니다. 블록체인과 머신 II라는 병리학적 난수 생성기를 결합하면 매우 범용적인 "모호한 장치"를 만들 수 있습니다. 여기에서 TEE에서 실행되는 데모를 볼 수 있습니다 여기.
자동화된 마켓 마이커(AMM)의 아이디어는 다음과 같습니다. 유동성 공급자(LP)가 수익을 얻으려 하지만 트레이더가 수익성 영역에서 "배제"할 수 있는 고전적인 배제 게임으로 LP를 다룬다고 가정해 보겠습니다. 게임은 LP의 딜레마를 기본적으로 다음과 같이 모델링합니다:
- 차익 거래 보호를 위해 높은 수수료를 부과하지만 소매 투자자를 놀라게 할 위험이 있습니다.
- 소매 투자자를 유치하기 위해 낮은 수수료를 부과하지만 차익 거래에 노출됩니다.
이러한 게임에서 모호한 장치("수수료 가리기")를 사용하면 LP의 상황을 실제로 개선할 수 있습니다. 수학은 다소 지루하고 익숙하지 않을 수 있으므로, 가려진 수수료가 게임에 미치는 영향을 그림으로 보여주는 것이 유용할 것 같습니다.
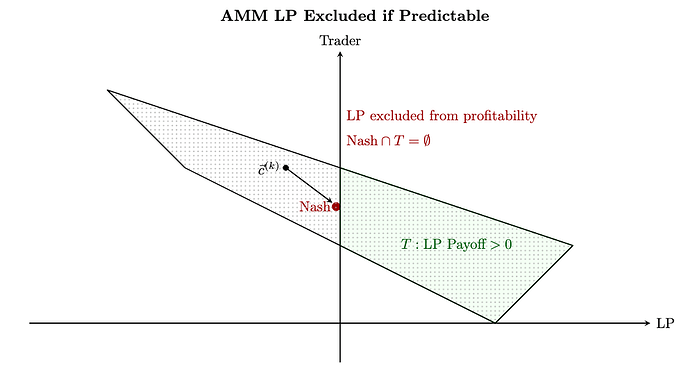
아래는 "문제 그림"으로, LP가 수익성 있는 전략이 없음을 보여줍니다. 유일한 내쉬 균형은 \le 0≤를 지불하므로 녹색 영역(TT)에서 배제됩니다.
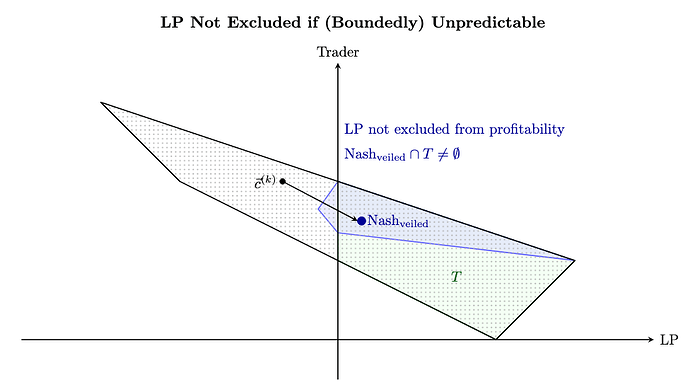
가려진 수수료를 도입하면 LP의 수익은 고정되지 않고 이제 전체 파란색 영역에 있습니다. 분명히 LP는 더 이상 수익성 있는 영역 TT에서 배제되지 않습니다(사실 오른쪽 끝에서 가장 높은 가능한 수익까지 도달할 수 있습니다). 또한 파란색 영역은 왼쪽에서 명확하게 잘려 있으므로 LP는 이에 대해 거의 위험을 감수하지 않습니다.
실제 수익 숫자를 확립하려면 LP가 수익 불확실성을 정확히 어떻게 다루는지에 대한 가정을 해야 합니다. 분명히 LP는 앞선 그림의 내쉬 균형보다 파란색 영역을 개선으로 보지 않을 만큼 불확실성을 꺼리지는 않을 것입니다.
LP의 중립성을 가정하여 최상의 수익과 최악의 수익을 중간 지점에서 평가한다면, LP는 혼합 내쉬 균형에서의 0에서 가려진 내쉬 균형에서의 1.4로 수익을 개선합니다.
초안 논문을 여기에서 더 자세히 읽을 수 있습니다. 지금까지 고급 암호화폐 두뇌 트러스트의 상당한 비율에게 이 접근 방식을 설명했으며, 아직까지 실질적인 이의가 제기되지 않았습니다. 유일한 혼합 전략 내쉬 균형을 파레토 지배할 수 있다는 점이 일부에게는 충격적일 수 있습니다(제가 처음 보았을 때도 그랬습니다). 하지만 2025년 현재 이는 주류 - 비록 최첨단 - 게임 이론입니다.