유익한 토론과 기사 검토를 해주신 Alex, Csaba, Dmitry, Mikhail 및 Potuz에게 진심으로 감사드립니다.
추상적인
이더리움의 현재 DAS 방식은 리드-솔로몬(Reed-Solomon) 삭제 코딩 + KZG 커밋을 기반으로 합니다. 이 새로운 방식(여기서는 @potuz 가 작성한 "이더리움에서 더 빠른 블록/블롭 전파(Faster block/blob propagation in Ethereum )" 참조)은 또 다른 쌍, 즉 RLNC(Random Linear Network Coding) 삭제 코딩 + 페데르센 커밋을 도입합니다. 이 방식은 대안적인 데이터 가용성 방식을 고려하는 데 사용될 수 있는 유용한 특성을 가지고 있습니다.
이 글에 설명된 프로토콜은 주로 RLNC 기반 데이터 가용성 설계가 어떤 모습일지 간략하게 보여줍니다. 여기에 사용된 개념들은 아직 충분히 검증되지 않았으며, 공식적으로 증명된 것은 더더욱 아닙니다. 어쨌든 이러한 개념들이 옳다고 판명된다면, 이 알고리즘은 프로토타입 개발의 기반이 될 수 있습니다. 만약 일부 개념이 틀렸다고 판명된다면, 알고리즘을 수정하거나 수정 또는 교체하는 것을 고려할 수 있습니다.
이 글의 논리는 여러 면에서 @Csaba 의 최근 게시물인 FullDASv2를 이용한 블롭 스케일링 가속화(getBlobs, mempool 인코딩, 아마도 RLC 사용) 와 겹칩니다 .
_추론과 토론 의견을 포함한 전체 맥락을 알아보려면 이 글의 확장 버전을 참조하세요: https://hackmd.io/@nashatyrev/Bku-ELAA1e_
소개
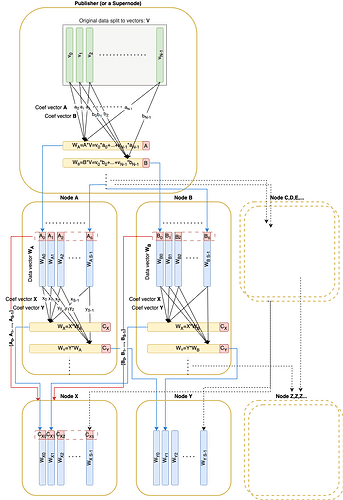
이더리움 에서 더 빠른 블록/blob propagation in Ethereum) 와 마찬가지로, 원본 데이터는 필드 F_p F p 에 대해 N N 개의 벡터 v_1, \dots, v_N v 1 , … , v N 으로 분할됩니다. 이러한 벡터는 RLNC를 사용하여 코딩할 수 있으며, 블록 에 포함된 페데르센 커밋(크기 32 \times N 32 × N )을 통해 커밋됩니다. 커밋과 관련 계수가 주어지면 모든 선형 조합을 검증할 수 있습니다.
또한 계수는 크기가 단일 바이트나 심지어 단일 비트(Bit) 만큼 작은 훨씬 더 작은 부분 필드 \mathbb{C}_q C q 에서 나올 수 있다고 가정합니다( 면책 조항: 최근 논의에 따르면 그렇게 작은 부분 필드가 있는 필드에 대해 안전한 EC를 가질 수 있다는 것이 확인되지 않았습니다).
또한 샤딩 요소 S S 를 소개해 드리겠습니다. 모든 일반 노드는 원래 데이터 크기의 1/S 1 / S 를 다운로드하고 보관해야 합니다.
고정된 샤드 인자 S S를 갖는 경우 원래 벡터의 총 수 N = S^2 N = S 2를 취해 보겠습니다.
간략한 프로토콜 개요
Pedersen 커밋(크기 32*N 32 ∗ N )은 해당 블록 에 게시됩니다.
전파 중에 각 노드는 피어로부터 의사난수 선형 조합 벡터를 수신합니다.
- 이 알고리즘은 수신기의
nodeId에서 무작위 계수가 결정론적으로 파생되고RREF행렬 트릭이 사용되는 비대화형 접근 방식을 설명합니다( 면책 조항:RREF트릭이 안전하게 작동하는지 엄격하게 증명되지 않았지만 증명 시작 아이디어가 될 수 있는 예가 있습니다) - 사용 가능한 대체 옵션도 있습니다. 응답자가 먼저 소스 계수를 공개하고, 요청자가 로컬에서 생성된 난수 계수를 사용하여 선형 조합을 요청하는 대화형 접근 방식입니다.
전송된 모든 선형 결합 벡터에는 해당 벡터가 무작위로 샘플링된 부분 공간의 기저 벡터가 수반됩니다. 이러한 기저 벡터는 RREF 형태의 행렬을 형성해야 합니다. 이 조건은 원격 피어가 실제로 요청된 부분 공간에 대한 기저 벡터를 소유하고 있음을 보장합니다.
노드는 다음 두 조건이 모두 충족될 때까지 샘플링을 계속합니다.
- 수신된 모든 기저 벡터는 전체 N N 차원 공간을 포괄합니다.
- 최소한 S S 구금 벡터가 수신되었습니다.
그 후, 노드는 샘플링을 완료하고 '활성' 노드가 되며, 다른 노드가 샘플링하는 데 사용될 수 있습니다.
메모
아래 Python 유사 코드 조각은 설명 목적으로만 제공되며, 현재로서는 컴파일 및 실행을 위한 것이 아닙니다. 일부 명확하거나 라이브러리 유사 함수는 아직 구현되지 않았습니다.
유형
데이터 벡터 요소가 대략 32바이트로 매핑될 수 있는 유한 필드 \mathbb{F}_p F p 에서 나오도록 하세요.
def FScalar계수 \mathbb{C}_q C q가 \mathbb{F}_p F p 의 부분체에서 나오도록 하세요.
def CScalar 단일 데이터 벡터가 \mathbb{F}_p F p 에서 VECTOR_LEN 요소를 갖도록 합니다.
def DataVector = Vector[FScalar, VECTOR_LEN] 전체 데이터를 N 원래 DataVector 로 나누면 다음과 같습니다.
def OriginalData = Vector[DataVector, N] 파생된 DataVector 는 원래 DataVector 의 선형 결합입니다. 원래 벡터는 파생된 벡터의 특수한 경우일 뿐이므로 더 이상 두 벡터를 구분하지 않겠습니다.
DataVector 커밋에 대해 검증하려면 선형 조합 계수를 알아야 합니다.
def ProofVector = Vector[CScalar, N] 기존 DataVector 에서 새로운 벡터를 유도할 때 사용되는 약간 다른 계수 시퀀스도 있습니다.
def CombineVector = List [CScalar]구조물
선형 조합 계수를 동반한 데이터 벡터
class DataAndProof :data_vector: DataVectorproof: ProofVector전달해야 할 유일한 메시지는
class DaMessage :data_vector: DataVector # coefVector for validation is derived orig_coeff_vectors: List [CombineVector]seq_no: Int블록 데이터를 위한 임시 저장소가 있습니다.
class BlockDaStore :custody: List [DataAndProof]sample_matrix: List [ProofVector] # commitment is initialized first from the corresponding block commitment: Vector[RistrettoPoint]기능
random_coef 함수가 시드 (nodeId, seq_no) 를 갖는 결정론적 난수 계수 벡터를 생성하도록 합니다.
def random_coef ( node_id: UInt256, length: int , seq_no: int ) -> CombineVector선형 조합을 계산하기 위해 유틸리티 함수를 정의해 보겠습니다.
def linear_combination ( vectors: Sequence [DataVector],coefficients: CombineVector ) -> DataVector def linear_combination ( vectors: Sequence [ProofVector],coefficients: CombineVector ) -> ProofVector DataVector 와 ProofVector 에 대해 동시에 선형 연산을 수행하여 ProofVector 를 RREF로 변환하는 함수:
def to_rref ( data_vectors: Sequence [DataAndProof] ) -> Sequence [DataAndProof] def is_rref ( proofs: Sequence [ProofVector] ) -> bool특정 피어에 대한 기존 보관 벡터에서 새로운 결정론적 무작위 메시지를 생성하는 기능:
def create_da_message ( da_store: BlockDaStorereceiver_node_id: uint256,seq_no: int ) -> DaMessage:rref_custody = to_rref(da_store.custody)rref_custody_data = [e.data_vector for e in rref_custody]rref_custody_proofs = [e.proof for e in rref_custody]rnd_coefs = random_coef(receiver_node_id, len (rref_custody), seq_no)data_vector = linear_combination(rref_custody_data, rnd_coefs) return DaMessage(data_vector, rref_custody_proofs, seq_no) 데이터 벡터 계수의 순위를 계산합니다. 순위가 N 이면 데이터 벡터에서 원본 데이터를 복원할 수 있음을 의미합니다.
def rank ( proof_matrix: Sequence [ProofVector] ) -> int게시하다
게시자는 OriginalData 얻기 위해 데이터를 벡터로 분할해야 합니다.
데이터 자체를 전파하기 전에 게시자는 Pedersen 커밋(크기 32 * N )을 계산하고, 이러한 커밋을 포함하는 블록 빌드하고 게시해야 합니다.
그런 다음 게시자는 보관을 데이터 벡터(원본)와 표준 기준의 요소인 '증명'으로 채워야 합니다. [1, 0, 0, ..., 0], [0, 1, 0, ..., 0] :
def init_da_store ( data: OriginalData, da_store: BlockDaStore ): for i,v in enumerate (data):e_proof = ProofVector([CScalar( 1 ) if index == i else CScalar( 0 ) for index in range (size)])da_store.custody += DataAndProof(v, eproof) 게시 프로세스는 기본적으로 전파 프로세스와 동일하지만, 게시자는 전파 중에 1개의 메시지만 보내는 대신 단일 라운드에서 단일 피어에게 S 메시지를 보냅니다.
def publish ( da_store: BlockDaStore, mesh: Sequence [Peer] ): for peer in mesh: for seq_no in range (S):peer.send(create_da_message(da_store, peer.node_id, seq_no))받다
해당 블록 수신되었고 BlockDaStore.commitment 가 message: DaMessage
원래 벡터에서 ProofVector 도출합니다.
def derive_proof_vector ( myNodeId: uint256, message: DaMessage ) -> ProofVector:lin_c = randomCoef(myNodeId, len (message.orig_coefficients),message.seq_no) return linear_combination(message.orig_coefficients, lin_c)검증하다
메시지가 먼저 검증되었습니다.
def validate_message ( message: DaMessage, da_store: BlockDaStore ): # Verify the original coefficients are in Reduced Row Echelon Form assert is_rref(message.orig_coefficients) # Verify that the source vectors are linear independent assert rank(message.orig_coefficients) == len (message.orig_coefficients) # Validate Pedersen commitment proof = derive_proof_vector(my_node_id, message)validate_pedersen(message.data_vector, da_store.commitment, proof)가게
수신된 DataVector 보관소에 추가됩니다.
sample_matrix 는 모든 원래 계수를 누적하고 행렬 순위가 N 에 도달하자마자 샘플링 프로세스가 성공합니다.
def process_message ( message: DaMessage, da_store: BlockDaStore ) -> boolean:da_store.custody += DataAndProof(message.data_vector,derive_proof_vector(my_node_id, message))da_store.sample_matrix += message.orig_coefficientsis_sampled = N == rank(da_store.sample_matrix) return is_sampled is_sampled == true 메시지를 보낸 피어가 데이터를 복구하는 데 필요한 정보를 전체적으로 100% 보유하고 있다는 것을 [거의] 100% 확신한다는 것을 의미합니다.
전파하다
process_message() 가 True 반환하면 샘플링이 성공적으로 완료되었고, 보관 공간이 충분한 수의 벡터로 채워졌음을 의미합니다. 이제 노드는 자체 벡터를 생성하고 전파할 수 있습니다.
우리는 아직 우리에게 벡터를 보내지 않은 메시의 모든 피어에게 벡터를 보냅니다.
# mesh: here the set of peers which haven't sent any vectors yet def propagate ( da_store: BlockDaStore, mesh: Sequence [Peer] ): for peer in mesh:peer.send(create_da_message(da_store, peer.node_id, 0 ))실행할 수 있음
원래 데이터 크기가 32Mb 라고 가정 하고 S S 와 |\mathbb{C}_q| | C q | (계수 크기)에 따라 몇 가지 숫자를 살펴보겠습니다.
| 봄 여름 시즌 | sizeOf(C) (비츠(Bits)) | 엔 엔 | 벡터 크기(KB) | 커밋 크기(KB) | 메시지 계수 크기(Kb) | 메시지 오버헤드(%%) |
|---|---|---|---|---|---|---|
| 8 | 1 | 64 | 512 | 2 | 0.0625 | 0.01% |
| 8 | 8 | 64 | 512 | 2 | 0.5 | 0.10% |
| 8 | 256 | 64 | 512 | 2 | 16 | 3.13% |
| 16 | 1 | 256 | 128 | 8 | 0.5 | 0.39% |
| 16 | 8 | 256 | 128 | 8 | 4 | 3.13% |
| 16 | 256 | 256 | 128 | 8 | 128 | 100.00% |
| 32 | 1 | 1024 | 32 | 32 | 4 | 12.50% |
| 32 | 8 | 1024 | 32 | 32 | 32 | 100.00% |
| 32 | 256 | 1024 | 32 | 32 | 1024 | 3200.00% |
| 64 | 1 | 4096 | 8 | 128 | 32 | 400.00% |
| 64 | 8 | 4096 | 8 | 128 | 256 | 3200.00% |
| 64 | 256 | 4096 | 8 | 128 | 8192 | 102400.00% |
이러한 수치에 따르면 S \ge 64 S ≥ 64 에서는 이 알고리즘을 사용하는 것이 기본적으로 불가능합니다. 작은 계수(1비트 또는 8 비츠(Bits))를 사용할 수 있는 옵션이 없다면, 계수 크기 오버헤드를 고려했을 때 S = 8 S = 8 이 합리적인 최대 샤딩 계수입니다. ( S = 16 S = 16 일 경우, 최소 노드 다운로드 처리량은 S = 8 S = 8일 때와 동일합니다.)
장단점
장점
- 배포, 보관 및 샘플링할 총 데이터 크기는 원래 데이터 크기의 x1(+ 작은 계수가 사용 가능한 경우 작을 수 있는 계수 오버헤드)입니다(PeerDAS의 경우 x2, FullDAS의 경우 x4와 비교).
- 잠재적으로 ' 샤드 팩터' S S가 최대 32(혹은 알고리즘에 다른 수정을 가하면 더 커질 수도 있음)만큼 커질 수 있는데, 이는 모든 노드가 원본 데이터 크기의 1/S 1 / S 만큼만 다운로드하고 보관하면 된다는 것을 의미합니다. (현재 PeerDAS 방식에서는 1/8 1 / 8 : 원본 64개에서 8개 열)
- 데이터는 사용 가능하며 모든 S S 정규 정직 노드가 성공적으로 샘플링을 수행하면 복구할 수 있습니다.
- 샘플링은 모든 S S 정규 노드를 사용하여 수행될 수 있습니다(현재 DAS에서 샘플링 노드가 서로 다른 DAS 서브넷의 다양한 피어를 필요로 하는 것과 비교).
- '샘플링한 내용을 보관하고 제공하는 것'(PeerDAS 서브넷 샘플링과 유사하지만 전체 샤딩 피어 샘플링과는 다름)이라는 접근 방식입니다. 여기에 설명된 피어 샘플링 접근 방식에 대한 우려 사항
- 열 슬라이싱이 포함되지 않으므로 별도의 블롭이 여러 원본 데이터 벡터에 걸쳐 있을 수 있으며 따라서 샘플링 프로세스는 EL 블롭 트랜잭션 풀(일명
engine_getBlobs())로부터 잠재적으로 효과적으로 이점을 얻을 수 있습니다. - Sybil 공격에 취약할 수 있는 더 작은 서브넷은 없습니다.
- 노드가 모든 피어로부터 S S 메시지를 필요로 하고 RLNC 코딩을 사용하기 때문에 전송 수준에서 데이터 중복이 잠재적으로 더 낮을 수 있습니다.
- RLNC + Pedersen은 RS + KZG보다 리소스 소모가 적을 수 있습니다.
단점
- 커밋과 증명 크기는 샤딩 계수 S S 에 따라 2차적으로 증가합니다.
- 더 작은 계수를 사용할 수 없는 경우(안전성이 입증되지 않은 경우) S=8 S = 8 만 가능합니다.
- 노드가 자체 샘플링을 완료한 후에만 데이터를 전파할 수 있으므로 여전히 보급 지연 시간을 추정해야 합니다.
- 행복한 경우 샘플링을 위한 최소 피어 수는 32개입니다(PeerDAS의 8개와 비교).
증명해야 할 진술
위 알고리즘은 지금까지 증명이 필요한 여러 가지 [아직 모호한] 진술에 의존합니다.
- 요청된 난수 계수를 슈퍼 노드가 반환한 유효한 선형 조합은 응답 노드가 전체 데이터(복구에 필요한 충분한 벡터)에 접근할 수 있음을 증명합니다. 이 명제는 증명하기 그렇게 까다로워 보이지 않습니다.
- 만약 전체 노드가 계수 부분 공간을 형성하는 기저 벡터를 가지고 있다고 주장할 때, 노드가 이 부분 공간에서 랜덤 벡터를 요청하여 유효한 데이터 벡터를 얻으면, 응답 노드가 실제로 해당 부분 공간에 대한 기저 벡터를 가지고 있음을 증명합니다. 이 증명은 다음 명제 (1)을 일반화한 것일 수 있습니다.
- 부분 필드 \mathbb{C}_2 C 2를 갖는 \ mathbb{F}_p F p 에 대한 EC는 의미가 있고 안전합니다. ( 최근 논의에 따르면 이는 사실이 아닌 것으로 보입니다 .)
- 실제로 RREF 기반 형식을 사용하여 RRT 샘플링을 수행하는 방법이 효과적입니다.
(이 예는 이 진술의 타당성에 대한 직관을 제공할 수 있습니다) - 설명된 알고리즘은 전체
N차원 공간에 대해 노드 전체에 고르게 분포된 기저 벡터를 생성합니다.E는 매우 작으므로(1~3 정도), 무작위로 선택된S + E개 노드의 기저 벡터 순위는 '매우 높은' 확률로N됩니다. 비잔틴 환경에서도 마찬가지입니다.