인식론적 상태: 초기 탐색
최근 이더리움의 슬롯 시간을 더 적극적으로 줄이는 방법에 대한 논의가 있었습니다. 이는 두 가지 방법으로 수행할 수 있습니다:
- 최대 예상 네트워크 대기 시간에 대한 가정인 \delta 매개변수 줄이기. 이는 대기 시간을 줄이는 p2p 계층의 개선이 있는 경우에만 안전하게 수행할 수 있습니다
- 한 슬롯의 네트워크 대기 시간 라운드 수를 줄이기 위해 슬롯 구조 재설계.
(1)을 가능하게 하는 상당한 p2p 강화 및 최적화 작업이 진행 중입니다. 상당한 속도 향상을 가능하게 하는 최상의 후보는 소거 코딩입니다. 연구 작업은 (2)에 집중되고 있습니다.
이 게시물은 (2)에 대한 최적의 접근 방식이 3SF에서 도입된 슬롯과 완결성 간의 긴밀한 결합에서 다소 벗어나, 대신 더 분리된 LMD GHOST 포크 선택 규칙과 참여자 수가 다른 완결성 가젯을 가질 수 있음을 주장할 것입니다.
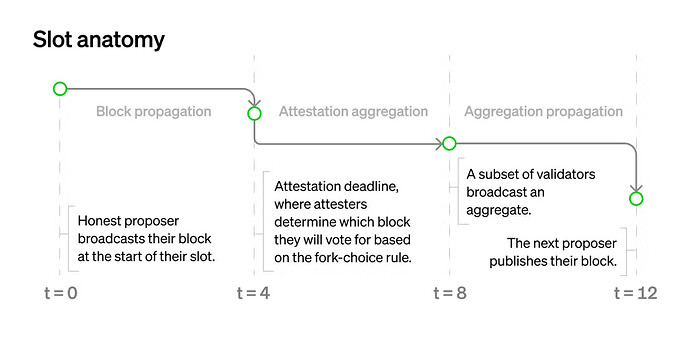
먼저 현재 슬롯 구조를 살펴보겠습니다:
여기서 \delta는 4초입니다. 첫 번째 섹션(블록 전파)은 피할 수 없습니다. 이제 증명과 관련된 두 단계가 있음을 주목하세요: 집계 및 전파. 이는 너무 많은 증명(슬롯당 약 30,000개)을 직접 공유할 수 없기 때문에 발생합니다. 대신 먼저 서브넷 내에서 하위 집합을 브로드캐스트한 다음 글로벌 p2p 네트워크 내에서 집계를 브로드캐스트합니다.
검증자 수를 훨씬 더 늘리면(예: 슬롯당 100만 명) 각 단계의 크기를 관리 가능하게 유지하기 위해 세 단계로 올라가야 할 수 있습니다(실제로 이전 글에서 정확히 이를 제안했습니다).
일반적으로 다음과 같이 근사할 수 있습니다:
집계_시간 = log_C(검증자_수)
여기서 C는 용량: 단일 서브넷 내에서 많은 서명을 동시에 안전하게 브로드캐스트할 수 있습니다. C의 현실적인 값은 수백 또는 수천 단위로 보입니다. 양자 저항성을 원한다면 더 보수적인 숫자를 가정해야 합니다(예: 양자 저항성 서명이 3KB를 차지하고 슬롯당 256개가 있다면 슬롯당 768kB로, 최악의 경우 실행 블록 크기와 비슷합니다).
완결성은 "전체 검증자 세트"의 참여에 따라 달라집니다. 스테이킹 중앙화 수용 또는 의무 위임이나 Orbit을 수행하는 경우 약 8,192개, 그렇지 않으면 훨씬 더 많은(10^5에서 10^6) 수가 될 것입니다. 즉, C^2 또는 C^3가 됩니다.
한편, 안정적인 LMD GHOST 인스턴스는 무작위로 선택된 정족수의 참여만 필요로 합니다. 여기서 크기 256(즉, C보다 작음)은 매우 낮은 실패율을 달성하기에 충분합니다.
이는 슬롯당 한 단계의 완결성 합의를 시도하는 모든 접근 방식이 본질적으로 3C 또는 4C(제안자를 위한 1C 추가)가 소요된다는 것을 의미합니다. 반면 그렇게 하지 않으면 한 단계가 2C만 소요됩니다.
제 핵심 제안은 다음과 같습니다:
- 슬롯당 약 256개의 검증자가 무작위로 선택되는 LMD GHOST 체인을 만듭니다. 이를 기본 "심장박동"으로 사용합니다
- 완결성 합의 메커니즘을 밀접하게 뒤따르게 합니다(현실적으로 12C에서 완결). 모든 활성 검증자를 사용합니다. LMD GHOST 투표와 완결성 합의 투표를 결합하지 말고 완전히 분리된 것으로 취급합니다.
이는 다음과 같은 이점을 제공합니다:
- 집계 단계가 슬롯 시간의 일부가 아니므로 보안 가정을 변경하지 않고도 충분히 빠른 정상 사례의 슬롯 시간
- 완결성 합의 메커니즘을 자유롭게 선택할 수 있음(예: Tendermint와 같은 기성 전통적인 방식)
- 비활성 누수를 처리하는 자연스러운 방법: 비활성 누수 중에 LMD GHOST 체인은 계속되고 완결성 합의는 중지됩니다. LMD GHOST 체인 자체가 비활성 누수의 진행을 결정하고 완결성을 복구할 수 있는 시기를 결정합니다.
- 완결성 단계에 대해 더 야심찬 선택을 할 수 있는 더 많은 자유(예: 1 ETH 검증자 요구 및 100만 검증자)
- 상호 작용 효과가 적고 Orbit과 같은 기술 없이 더 높은 검증자 수를 얻을 수 있기 때문에 더 단순함.