저자: NIFTY

샌프란시스코에 위치한 비트코인 전용 코워킹 스페이스인 프레시도 비트코인(Presido Bitcoin)은 지난주 비트코인과 양자 컴퓨팅에 대한 업계 컨퍼런스를 개최했습니다. btcd 및 lnd 클라이언트의 수석 유지 관리자이자 Lightning Labs 의 CTO인 @roasbeef 는 비트코인에 양자 안전 서명 체계인 SPHINCS+를 추가하는 방안을 제안했습니다. 오늘 보도에서 인사이더(Insider)의 프로토콜 전문가 @niftynei는 이 제안에 대해 설명합니다.
양자 보안 문제
온체인 대부분의 자금은 개인 키로 보호됩니다. 블록체인에서 비트코인 거래(자금 이체)를 확인하려면 서명을 통해 자금 사용 권한을 증명해야 합니다. 유효한 서명은 올바른 개인 키에 접근할 수 있는 사람만 생성할 수 있습니다.
어떤 의미에서 비트코인은 "난독화를 통해 보안"을 달성합니다. 여기서 "난독화"란 개인 키를 추측하기 어렵게 만드는 것을 의미합니다. 개인 키가 될 수 있는 숫자의 수는 천문학적입니다. 개인 키 하나를 추측하는 데는 엄청난 시간과 노력이 필요하기 때문에, 합리적인 시간(예: 수백 년) 내에는 누구도 이를 달성할 수 없습니다.
하지만 현재 비트코인 키는 타원 곡선 기반 수학 방정식에 의존합니다. 타원 곡선은 공개 키와 개인 키를 생성하는 데 적합한데, 일반적으로 소수 인수분해(공개 키와 개인 키 암호화의 기반이 되는 또 다른 "수학적 체계")보다 안전하고, 공개 키와 개인 키의 크기도 더 작기 때문입니다.
하지만 타원 곡선 암호에도 문제가 있습니다. 1994년 피터 쇼어(Peter Shor) 가 발명한 쇼어 알고리즘은 푸리에 변환을 기반으로 하며, 충분한 양자 비트(큐비트)를 가진 양자 컴퓨터는 모든 공개 키의 개인 키를 빠르게 계산할 수 있습니다.
쇼어 알고리즘은 타원 곡선 암호를 해독하는 방법을 알고 있지만 , 이를 위한 도구는 아직 존재하지 않는다는 것을 의미합니다. 그러한 도구가 등장할지, 그리고 언제 등장할지 여부는 비트코인 커뮤니티뿐만 아니라 더 넓은 암호학 커뮤니티 내에서도 뜨거운 논쟁거리입니다. 비트코인을 저장하는 데 사용되는 모든 개인 키의 보안은 쇼어 알고리즘을 실행할 수 있는 도구에 아무도 접근할 수 없다는 사실에 달려 있습니다.
비트코인은 언젠가 는 양자 이후 공개-개인 키 암호화 시스템으로 전환해야 할 것이라는 것이 일반적인 의견입니다. 지난주 프레시디오에서 @roasbeef가 제안한 내용은 "SPHINCS+" 해시 서명 체계를 기반으로 했습니다. 이 체계의 작동 방식과 비트코인 보안에 적합한 이유를 간략히 살펴보겠습니다.
양자 보안, 하지만 데이터 부담이 크다
SPHINCS+는 해시 기반 서명 구조입니다. 핵심적으로, 공개 키를 생성하고 서명을 검증하기 위해 (우아한 타원 곡선 방정식이나 비밀 소인수분해가 아닌) 암호화 해시 함수에 의존합니다. 해시 기반 암호화 체계는 단방향 함수에 함수형 수학적 시스템을 사용하지 않기 때문에 쇼어 알고리즘의 영향을 받지 않습니다. 대신, 해시 함수는 무차별 대입(brute-force) 방식의 원상 스태킹(preimage stacking)에 의존합니다. 무차별 대입 방식은 양자 푸리에 변환에 취약한 수학적 관계(또는 지름길)를 포함하지 않으므로 쇼어 알고리즘의 영향을 받지 않습니다.
데이터 스태킹 또는 해싱 함수에는 단점이 있습니다. 공개 키와 서명을 공유하려면 훨씬 더 많은 데이터가 필요합니다. 사토시 나카모토 비트코인에 타원 곡선을 선택한 이유는 타원 곡선 기반 암호화가 서명을 검증하고 자금을 공개 키에 고정할 때 공유해야 하는 데이터가 더 적기 때문입니다. 저는 비트코인이 타원 곡선 암호화의 킬러 앱이라고 말하고 싶습니다. 사토시 나카모토 대부분의 암호화 시스템이 RSA(또는 소인수분해)를 기본 수학 시스템으로 사용했습니다. SEC 2 매개변수 논문에 따르면, 128비트 서명 보안을 달성하려면 RSA 공개 키는 3072비트 길이여야 하는 반면, 타원 곡선 공개 키는 256비트만 필요합니다.

블록체인 시스템에서는 작은 크기가 매우 중요합니다. 온체인 에 추가되는 모든 데이터는 네트워크의 모든 피어에게 전송되고 저장되어야 하기 때문입니다. 서명과 공개 키 크기가 작기 때문에 동일한 데이터 공간에 더 많은 거래를 담을 수 있습니다. 이러한 크기 감소는 사토시 나카모토 비트코인에 RSA 대신 타원 곡선 암호화를 선택한 이유 중 하나라고 할 수 있습니다.
이에 비해 포스트 양자 암호화 시스템의 공개 키와 서명은 엄청나게 큽니다. SPHINCS+ 시스템의 공개 키는 비트코인의 현재 키 시스템과 크기가 같지만, 서명은 수천 바이트에 달합니다. Segregated Witness v1(Taproot라고도 함)의 Schnorr 서명은 64바이트이고, 벤치마크 SPHINCS+ 서명은 3~7KB입니다.
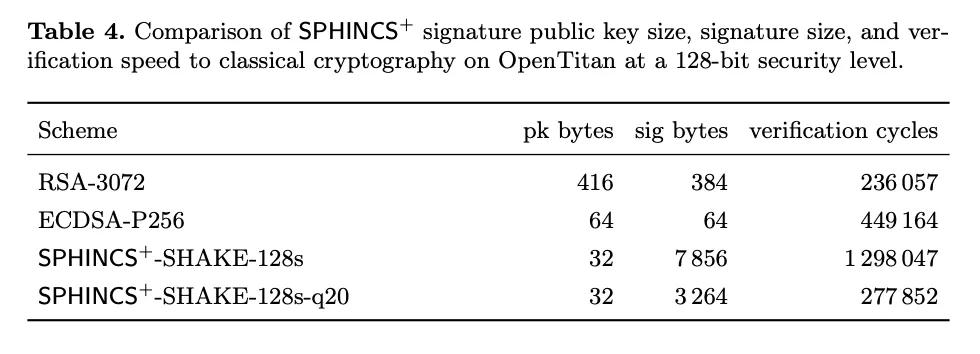
- NIST SPHINCS+ 매개변수 논문 에서 -
스핑크스+
SPHINCS+는 여러 계층의 포스트 양자 서명 "가젯"을 사용하여 개발된 복잡한 서명 체계입니다. 이 가젯들을 결합하면 여러 메시지에 안전하게 서명할 수 있는 양자 안전 공개/개인 키 쌍이 생성됩니다. 이전 버전인 "확장 머클 서명 체계(XMSS)"(해시 기반 포스트 양자 서명 체계)와 달리, SPHINCS+는 키 쌍을 위해 생성된 서명을 기억할 필요가 없습니다.
SPHINCS+ "구조"는 개인 키를 공개하지 않고도 여러 메시지에 서명할 수 있는 공개 키를 생성할 수 있습니다.
SPHINCS+ "구조"는 세 부분으로 구성됩니다.
FORS는 "무작위 부분 집합의 숲(Forest of Random Subsets)"의 약자입니다. 이는 SPHINCS+ "구조"의 기본 계층으로, 메시지를 사용하여 어떤 원상(preimage)을 공개할지 결정합니다. 공개된 원상 집합은 SPHINCS+ 서명의 기반이 됩니다. SPHINCS+에서 메시지는 실제로 FORS를 사용하여 "서명"됩니다. 다음 섹션에서는 FORS 서명을 SPHINCS+ "상부 구조"(제가 이렇게 부르기로 했습니다)의 루트 공개 키에 연결하는 방법을 다루겠습니다.
WOTS+(Winternitz One-Time Signature Plus)는 메시지에 안전하게 서명할 수 있는 포스트퀀텀 해시 기반 서명 알고리즘입니다. SPHINCS+는 WOTS+ 서명을 사용하여 FORS에서 공개된 프리이미지를 계층적 XMSS 머클 트리에 바인딩합니다. 이 계층적 머클 트리의 루트는 SPHINCS+ 공개 키입니다. (WOTS와 WOTS+의 유일한 차이점은 "+" 변형이 각 해시 연산에 무작위 접두사를 포함하여 다중 대상 해시 공격을 완화한다는 것입니다. "SPHINCS+"의 "+"는 각 해시 연산에 무작위로 생성된 접두사가 포함된다는 것을 의미하기도 합니다.)
XMSS 머클 트리. XMSS 머클 트리의 각 리프는 WOTS+ 공개 키입니다. SPHINCS+는 XMSS 머클 트리의 여러 레이어를 사용하여 거대한 피라미드 구조를 만듭니다. 트리 위에 트리가 겹쳐져 있는 구조는 종종 "하이퍼트리"라고 합니다. 부모 트리의 각 리프는 WOTS+ 공개 키이며, 이 키는 아래 트리의 루트에 서명하여 트리를 하나로 묶어 구조를 형성합니다. 트리의 수와 레이어 수는 SPHINCS+ "하이퍼구조"에 필요한 서명 크기에 따라 달라질 수 있습니다. 원하는 서명 크기가 작을수록 서명을 검증하고 생성하는 데 더 많은 해시가 필요합니다. 모든 트리의 최하위 레벨에 있는 각 리프는 FORS입니다. 머클 트리와 레이어가 많으면 피라미드 하단에 많은 FORS가 존재하며, 이를 사용하여 재사용 가능성이 매우 낮은 안전한 서명을 생성할 수 있습니다.
(번역자 주: SPHINCS+ 구조를 "전체 트리"가 아닌 "피라미드"라고 부르는 이유는 실제로 잎에서 시작하여 레이어별로 병합되어 루트를 형성하는 단일 머클 트리와 같지 않기 때문입니다(따라서 루트는 최하위 레벨의 모든 잎에 커밋됩니다). 대신, 최상위 레이어의 XMSS 머클 트리의 각 잎은 WOTS+ 공개 키이고, 각 WOTS+ 공개 키는 두 번째 레이어의 XMSS 머클 트리 루트에 서명합니다 . 이러한 두 번째 레벨의 XMSS 머클 트리는 같은 방식으로 구성됩니다. 각 잎은 WOTS+ 공개 키입니다. 따라서 다음 레이어의 XMSS 머클 트리 수는 항상 이전 레이어의 수의 배수, 즉 피라미드입니다. 최하위 레이어는 XMSS 머클 트리가 아니라 FORS 머클 트리(포리스트)입니다. FORS 공개 키는 서명을 만드는 데 사용할 수 있는 여러 머클 트리에 해당합니다.)
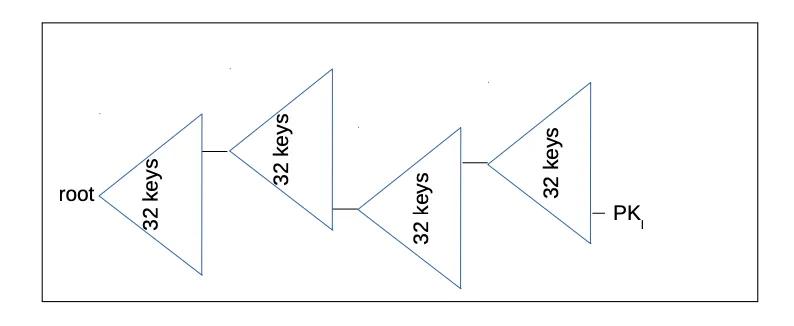
- 슈퍼트리 그래프를 지나치게 단순화한 버전입니다. 위 다이어그램의 PK는 실제로 SPHINCS+ 환경에서 FORS 서명입니다. "루트"는 SPHINCS+ 공개 키입니다. -
SPHINCS+ 공개 키를 생성하는 기본 과정은 트리의 루트에서 WOTS+ 공개 키를 생성한 다음, 이 트리들의 머클 루트를 계산하는 것입니다. 최상위 트리의 루트는 SPHINCS+ 공개 키입니다. 머클 트리 루트의 크기는 루트를 계산하는 데 사용된 해시 함수에 따라 결정됩니다. 일반적으로 256비트 출력을 갖는 SHA256 해시 함수가 사용됩니다. 즉, 이러한 머클 트리의 루트는 32바이트가 됩니다. 이렇게 하여 SPHINCS+ 공개 키가 생성됩니다.
SPHINCS+ 서명을 생성하려면 메시지 해시를 사용하여 SPHINCS+ 슈퍼트리에 조인할 FORS 서브트리를 무작위로 선택하고 FORS 서명을 생성해야 합니다. FORS 서명이 생성되면 상위 XMSS 트리에 있는 WOTS+ 공개 키의 개인 키로 서명됩니다. 이 서명은 트리를 따라 최상위 SPHINCS+ 공개 키에 도달할 때까지 공개 키의 머클 경로와 결합됩니다. 모든 WOTS+ 서명, FORS 서명, 그리고 FORS 서명에서 SPHINCS+ 공개 키로 이어지는 머클 경로의 조합이 메시지 서명을 구성합니다. 상상할 수 있듯이 이는 많은 양의 데이터이며, 이것이 SPHINCS+ 서명이 타원 곡선 서명(64바이트)보다 훨씬 큰 이유입니다.
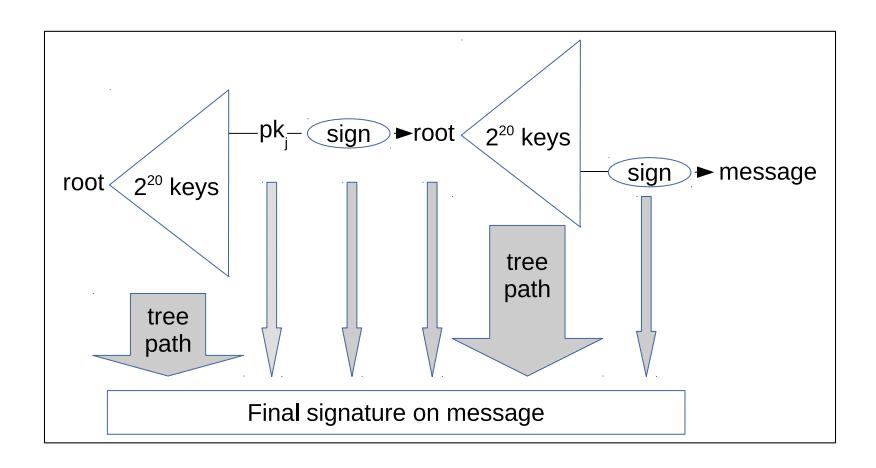
- SPHINCS+ 서명에 포함된 데이터의 개략도. 오른쪽의 "기호"는 FORS 서명을 생성하고, 가운데의 "기호"는 WOTS+ 서명을 생성합니다. -
왜 SPHINCS+를 사용해야 하나요?
SPHINCS+는 완전히 계층적이고 다루기 힘들며, Witnernitz 서명, FORS, XMSS 서브트리 등 여러 가지 "도구"를 사용하여 서명을 생성합니다.
SPHINCS+의 복잡성은 강력한 기능 세트에서 비롯됩니다. 이는 하나의 공개 키로 여러 메시지에 서명할 수 있도록 하는 포스트 양자 서명 방식인 XMSS를 엄격하게 최적화한 것이지만, 서명에 사용된 머클 트리 리프를 추적해야 합니다. SPHINCS+는 서명된 메시지의 다이제스트에서 생성된 난수를 사용하여 슈퍼트리 내의 서브트리 리프를 결정론적으로 선택합니다.
비트코인에서는 이상적으로 모든 거래에 대해 공개 키를 순환해야 합니다. 즉, 비트코인에서 사용되는 모든 공개 키에 대해 새로운 SPHINCS+ 슈퍼 구조를 생성해야 합니다.
처음에는 (이상적으로는) 일회용 공개 키에 이렇게 강력한 다중 서명 기능이 제공되는 이유가 무엇인지 혼란스러웠습니다.
Blockstream Research의 조나스 닉은 추가 수수료를 추가하거나 어떤 이유로 거래가 손실된 경우 다시 서명해야 한다고 지적했습니다. 라올루 (로즈비프라고도 함)는 라이트닝 네트워크와 같은 오프체인 프로토콜은 개인 계약 내의 상태 전환을 추적하기 위해 여러 서명(동일한 공개 키)이 필요하다고 지적했습니다.
비트코인에서는 무제한 재서명 기능이 필요하지 않을 가능성이 높으므로, 공개 키를 생성하기 위해 더 작은 SPHINCS+ 상부 구조를 구축할 수 있습니다. 상부 구조가 작을수록 필요한 머클 트리 경로가 줄어들어 서명의 양도 줄어듭니다. 하지만 이는 보안이 저하되기 전에 생성할 수 있는 서명의 개수가 줄어든다는 것을 의미합니다. 타원 곡선 암호에서는 서명 논스를 재사용하면 개인 키가 즉시 유출되지만, SPHINCS+에서는 공개 키(서명용)를 과도하게 사용하더라도 하위 레벨 FORS가 키의 일부를 재사용하기 시작하면서 128비트부터 보안이 점진적으로 저하됩니다.
더 깊이 파고들어 보니, 저는 Roasbeef의 SPHINCS+를 포스트 양자 서명 방식으로 사용하자는 제안에 매우 찬성합니다. 정확한 매개변수를 결정하기 위해서는 아직 설계 작업이 많이 남아 있습니다. 저는 초안 BIP(Roasbeef가 이미 진행 중이라고 언급)를 기대하고 있는데, 이는 상부 구조의 계층 수와 안전한 재서명 시도 횟수 간의 관계를 둘러싼 몇 가지 공백을 메우는 데 도움이 될 수 있을 것입니다.
roasbeef의 발표에서 언급했듯이, SPHINCS+는 시드/서브키 파생 경로를 허용하지 않는다는 점도 짚고 넘어가야 합니다. 이는 BIP32 계층형 지갑이 더 이상 유효하지 않음을 의미합니다. 대안은 있지만, 현재 업계에서 xpubs 및 서브월렛에 사용하는 것처럼 계층형 파생 경로를 사용하여 지갑을 구성하는 공개 키를 설명하는 기능은 더 이상 사용할 수 없게 됩니다.
어느 쪽으로 가야 하나요?
비트코인은 양자 서명 이후의 방식으로 전환될 것입니다. 언제, 어떤 방식을 사용할지, 그리고 어떤 매개변수를 적용할지는 향후 몇 년 동안 이슈 화두가 될 것입니다.
Roasbeef의 SPHINCS+ 제안은 다층 트리 구조의 복잡성에도 불구하고 매력적인 옵션입니다. 제 생각에는 해시 함수 기반 포스트 양자 공개 키 방식은 모두 끔찍합니다. SPHINCS+도 보기 흉하지만, 그 이유는 반복 서명 시 상태 비저장 기능을 포함하여 가장 많은 기능을 제공하기 때문입니다.
각 부분이 프로토콜에서 수행하는 역할을 더 잘 이해하게 되면서, 저는 이 다층적 구조를 설계하는 데 들어간 영리함을 크게 감사하게 되었습니다.
Roasbeef는 BIP에 대해 아직 많은 작업을 해야 합니다. 특히 각 트리의 깊이와 서브트리 레벨 수, Winternitz 서명 크기, 그리고 FORS 매개변수와 관련하여 더욱 그렇습니다. 서명 크기와 서명 생성에 필요한 해시 수 사이에는 딜레마가 존재합니다. 공식적인 BIP를 발표하기 전에 연산량과 온체인 추적성 간의 적절한 균형을 찾는 것이 매우 중요합니다.
그럼 마지막으로 한 가지 질문이 남습니다.
SPHINCS+로의 전환이 비트코인이 다단계 사기가 되었다는 것을 의미할까요? 정의하기는 어렵지만, 확실히 그런 것 같습니다.
(번역자 주: 이것은 말장난입니다. "피라미드 방식"은 "피라미드 방식"과 SPHINCS+의 "피라미드 구조"를 모두 의미할 수 있기 때문입니다.)
감사의 말
SPHINCS+ 공개 키 재사용 및 매개변수 튜닝에 대한 설명을 도와준 Jonas Nick과 Olaoluwa Osuntokun에게 감사드립니다.
추가 자료
더 자세히 알고 싶으신가요? 이 글의 참고 자료로 사용한 유용한 자료들을 소개합니다.
- 7월 17일 Presidio Bitcoin and Quantum Computing Conference에서 Laolu가 발표한 슬라이드
- Sphere10의 Winternitz 시그니처 설명은 제가 포스트 퀀텀 시그니처의 기본을 익히는 데 도움이 되었습니다.
- 소프트웨어 개발자 이선 란(Ethan Rahn)의 심도 있는 블로그 게시물에는 멋진 다이어그램과 양자 서명 개발에 대한 역사가 포함되어 있습니다.
- NIST의 존 켈시가 SPHINCS+ 에 대해 훌륭하고 심도 있게 설명한 글입니다. 제가 본 것 중 가장 자세한 설명 중 하나인데, 지금은 묻혀 있는 것 같습니다.
(위에)