이 글은 교환 거래소 증명의 기본 원칙을 설명하고 자산 보관 스펙트럼의 양끝인 CEX와 DEX의 중간에서 더 많은 가능성을 탐색하는 것을 목표로 합니다.
원문: 안전한 CEX 보유: 지급 능력 이상의 증명 (vitalik.ca)
저자: 비탈릭 부테린
번역: doublespending (@doublespending)
검토자: ECN
표지: Unsplash 의 Pawel Czerwinski 사진
토론에 참여해주신 Balaji Srinivasan과 Coinbase, Kraken 및 Binance 팀에 특별히 감사드립니다.
대규모 중앙화 거래소 충돌할 때마다 자주 묻는 질문은 암호화폐를 사용하여 문제를 해결할 수 있는지 여부입니다. 거래소 정부 라이선스, 감사, 기업 거버넌스 조사 및 거래소 법인 백체킹과 같은 "법적 통화" 솔루션에만 의존하기보다는 온체인 보유된 자금이 사용자에게 상환하기에 충분하다는 것을 증명하기 위해 암호화 증명을 만들 수 있습니다.
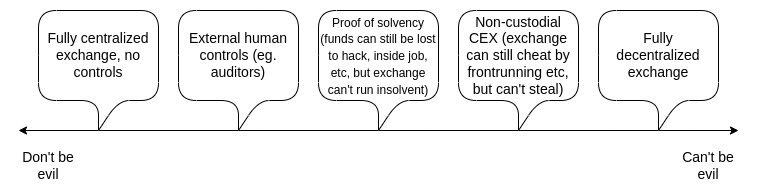
보다 야심차게, 거래소 예금자의 동의 없이 자금을 클레임 할 수 없는 시스템을 구축할 수 있습니다. 우리는 “악을 행하지 않는” 전문적인 CEX와 “악을 행할 수는 없지만” 프라이버시를 유출하는 비효율적인 온체인 DEX 사이의 경계를 탐색해 볼 수 있습니다. 이 기사에서는 CEX를 더욱 신뢰하지 않게 만들려는 역사적 시도, 채택하는 기술의 한계, ZK-SNARK와 같은 고급 기술에 의존하는 몇 가지 강력한 방법을 자세히 살펴보겠습니다.
잔액 대조표와 머클 트리: 전통적인 지급 능력 증명
사용자를 속이지 않는다는 것을 증명하기 위해 암호화를 사용하려는 거래소 의 초기 시도는 오래 전으로 거슬러 올라갑니다. 2011년 당시 가장 큰 비트코인 거래소 였던 MtGox는 424,242 BTC를 사전에 발표된 주소로 이동시키는 거래를 보냄으로써 자금을 소유하고 있음을 입증했습니다. 2013년에는 사용자 예치금의 총 규모를 입증하는 문제의 다른 측면을 해결하는 방법에 대한 논의가 시작되었습니다. 사용자의 예치금이 다음과 같다는 것을 증명하는 경우 거래소.
입금 증명을 제공하는 가장 쉬운 방법은 목록을 게시하는 것입니다. 각 사용자는 목록에서 자신의 잔액 확인할 수 있으며 누구나 전체 목록을 확인할 수 있습니다. (i) 각 잔액 은 음수가 아닙니다. (ii) 총액은 청구 금액입니다.
물론 이는 개인 정보 보호를 침해하므로 계획을 약간 변경할 수 있습니다. 목록을 게시하고 비공개로 솔트 값을 사용자에게 보냅니다. 하지만 이렇게 해도 잔액 과 분배가 누출될 수 있습니다. 개인정보 보호를 위해 후속 기술인 Merkle Tree 기술을 사용합니다.
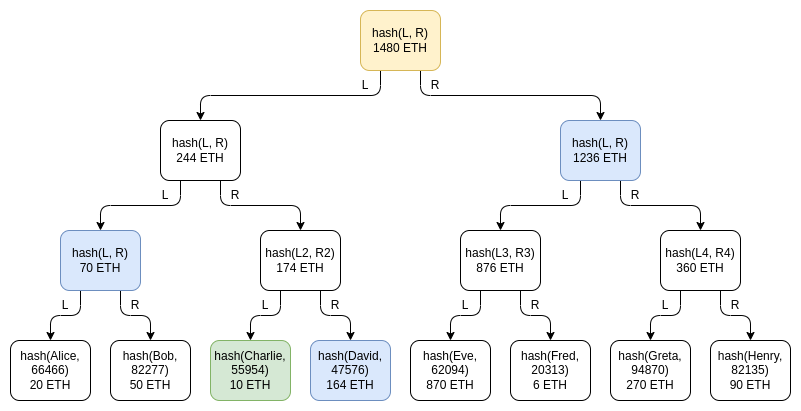
녹색: Charlie의 노드. 파란색: Charlie가 증명을 위해 노드를 받습니다. 노란색: 루트 노드, 모든 사람에게 공지됨
머클 트리 기술은 사용자 잔액 테이블을 머클 합계 트리에 배치합니다. Merkle 합계 트리에서 각 노드는 쌍입니다. 기본 리프 노드는 각 사용자의 잔액 과 사용자 이름의 솔트 해시를 나타냅니다. 각 상위 노드에서 잔액 아래 두 노드 잔액 의 합이고, 해시는 아래 두 노드의 해시입니다. Merkle 합계 증명은 Merkle 증명과 마찬가지로 리프 노드에서 루트 노드까지의 경로에 있는 모든 자매 노드로 구성된 "분기"입니다.
먼저, 거래소 각 사용자에게 잔액 에 대한 Merkle 증명을 보냅니다. 그러면 사용자는 잔액 총계의 일부로 올바르게 포함되었는지 확인할 수 있습니다. 간단한 예제 코드는 여기에서 찾을 수 있습니다.
# The function for computing a parent node given two child nodesdef combine_tree_nodes(L, R):L_hash, L_balance = LR_hash, R_balance = Rassert L_balance >= 0 and R_balance >= 0new_node_hash = hash(L_hash + L_balance.to_bytes(32, 'big') +R_hash + R_balance.to_bytes(32, 'big'))return (new_node_hash, L_balance + R_balance)# 전체 Merkle 트리를 구축합니다. 여기서 # 노드 i는 노드 2i의 부모이고 2i+1def build_merkle_sum_tree(user_table: "List[(사용자 이름, 소금, 잔액)]"):tree_size = get_next_power_of_2(len(user_table))tree = ([없음] * tree_size +[userdata_to_leaf(*user) for user in user_table] +[EMPTY_LEAF for _ in range(tree_size - len(user_table))])for i in range(tree_size - 1, 0, -1):tree[i] = Combine_tree_nodes(tree[i*2], tree[i* 2+1])return tree# 트리의 루트는 평면화된 형식으로 인덱스 1에 저장됩니다def get_root(tree):return tree[1]# 특정 인덱스에 있는 노드에 대한 증명을 가져옵니다def get_proof(tree, index):branch_length = log2(len(tree)) - 1# ^ = 비트 xor, x ^ 1 = xindex_in_tree의 자매 노드 = index + len(tree) // 2return [tree[(index_in_tree // 2**i) ^ 1] for i in range(branch_length)]# 증명 확인 (duh)def verify_proof(username, salt, Balance, index, user_table_size, root,proof):leaf = userdata_to_leaf(username, salt, Balance)branch_length = log2(get_next_power_of_2(user_table_size) ) - 1for i in range(branch_length):if index & (2**i):leaf = Combine_tree_nodes(proof[i], leaf)else:leaf = Combine_tree_nodes(leaf,proof[i])return leaf == root
이 설계에 따른 개인 정보 유출은 전체 잔액 테이블을 게시하는 것보다 훨씬 낮으며 Merkel 루트가 출시될 때마다 각 지점을 방해하여 개인 정보 유출 리스크 더욱 줄일 수 있지만 여전히 일부 개인 정보 유출 문제가 있습니다. Charlie는 다음을 알고 있습니다. someone 그 사람의 잔액 은 164 ETH이고, 두 명의 특정 사용자의 잔액 의 합은 70 ETH입니다. 여러 계정을 제어하는 공격자는 여전히 거래소 사용자에 대해 대량 배울 수 있습니다.
이 계획의 중요한 미묘한 점은 마이너스 잔액 의 가능성입니다. 사용자 잔액 1390 ETH이지만 보유량이 890 ETH인 거래소 트리 어딘가에 있는 가짜 계정에 -500 ETH 잔액 추가하여 보상을 시도하는 경우 어떻게 해야 합니까? 차이점은 무엇입니까? 이 가능성은 실제로 계획을 깨뜨리지 않으므로 우리는 일반 Merkle 트리 대신 Merkle 합계 트리를 특별히 사용합니다. Henry가 거래소 관리하는 가짜 계정이고 거래소 해당 계정에 -500 ETH를 배치한다고 가정합니다.
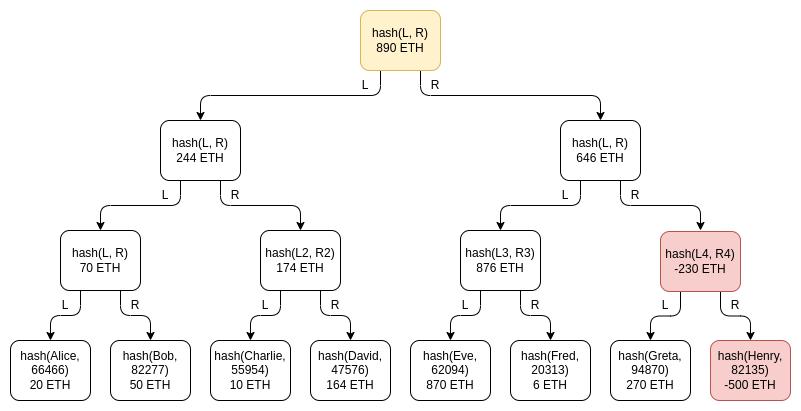
Greta의 검증은 통과되지 않습니다. 거래소-500 ETH 잔액 그녀에게 제공해야 할 때 Greta는 잘못된 노드를 거부합니다. Henry의 중간 노드 잔액 이 -230 ETH이므로 Eve와 Fred도 검증에 실패하므로 이 노드도 유효하지 않습니다! 도난이 발각되지 않도록 거래소 트리의 오른쪽 절반에 있는 누구도 잔액 증명서를 확인하지 않기를 바랄 뿐입니다.
거래소 잔액 증명을 확인하지 않거나 잔액 증명을 받지 못했다고 불평할 때 믿지 않는 500 ETH를 가진 사용자를 골라낼 수 있다면 거래소 이를 피할 수 있습니다. 그러나 거래소 Merkle 합계 트리에서 이러한 사용자를 제외하여 동일한 효과를 얻을 수도 있습니다. 따라서 부채 증명에 관한 한 머클 트리 기술은 기본적으로 요구 사항을 충족합니다. 그러나 개인 정보 보호 기능은 여전히 이상적이지 않습니다. 사토시(satoshi)나 웨이(wei)와 같은 머클 트리를 독립적인 리프 노드로 사용하여 개선할 수 있습니다. 그러나 더 발전된 기술을 사용하면 더 나은 결과를 얻을 수 있습니다.
ZK-SNARK를 사용하여 개인 정보 보호 및 견고성 향상
ZK-SNARK는 강력한 기술입니다. ZK-SNARK는 인공 지능과 마찬가지로 암호화에 있어서 다양한 문제를 해결하기 위해 수십 년 전에 개발된 수많은 특수 기술을 압도할 만큼 일반적인 기술입니다. 따라서 우리는 ZK-SNARK를 사용하여 부채 증명 프로토콜의 개인 정보 보호를 크게 단순화하고 향상시킬 수 있습니다.
우리는 모든 사용자 예치금을 Merkle 트리(또는 더 간단한 KZG 약속)에 넣고 ZK-SNARK를 사용하여 트리의 모든 잔액 음수가 아니며 일부 청구된 가치를 합산한다는 것을 증명할 수 있습니다. 개인 정보 보호를 보장하기 위해 해싱 계층을 추가하면 각 사용자에게 발행된 Merkle 분기(또는 KZG 증명)는 다른 사용자의 잔액 공개하지 않습니다.
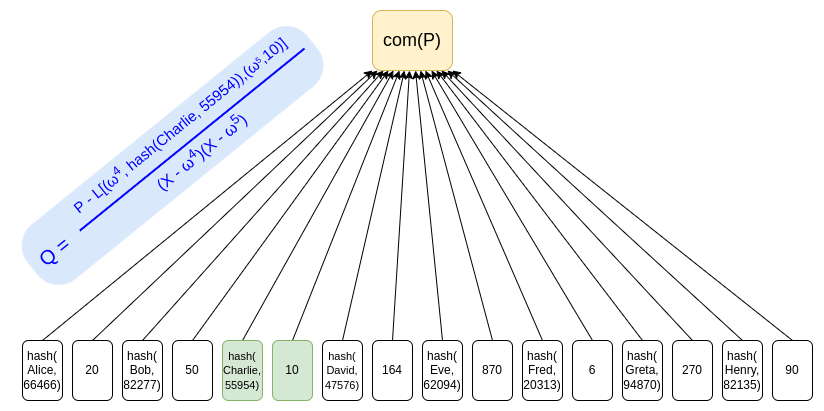
KZG 약정을 사용하는 것은 "자매 노드"를 증거로 제공할 필요가 없기 때문에 개인 정보 유출을 피하는 방법이며 간단한 ZK-SNARK를 사용하여 잔액 음수가 아니며 각 잔액 이 음수가 아닌.
전용 ZK-SNARK를 통해 위 KZG의 잔액 잔액 와 음수가 아님을 증명할 수 있습니다. 다음은 간단한 예입니다. 우리는 "사용자 잔액 의 각 비트를 구성"하는 보조 다항식 I(x)를 소개합니다(예를 들어 잔액 215 미만이라고 가정). 여기서 매 16번째 비트는 실제 합계가 다음과 같은 경우에만 보장되는 차이를 추적합니다. 청구된 것과 동일합니다. 총액이 동일한 경우에만 값이 0이 됩니다. z가 128차의 기본근이면 방정식이 다음과 같이 성립함을 증명할 수 있습니다.

이러한 방정식을 다항식으로 변환한 다음 ZK-SNARK로 변환하는 방법은 여기와 ZK-SNARK에 대한 내 기사의 다른 곳에서 찾을 수 있습니다. 이것은 최적의 프로토콜은 아니지만 이러한 암호화 증명을 더 쉽게 이해할 수 있게 해줍니다!
몇 가지 추가 방정식만 사용하면 제약 조건 시스템을 더 복잡한 설정에 적용할 수 있습니다. 예를 들어, 레버리지 거래 시스템에서는 개인 사용자가 마이너스 잔액 갖는 것이 허용되지만 부채를 감당할 만큼 충분한 담보 자산이 있는 경우에만 가능합니다. SNARK는 이러한 보다 복잡한 제약을 증명하는 데 사용될 수 있으며, 거래소 비밀리에 특정 사용자를 면제하여 사용자 자산을 위험에 빠뜨릴 수 없음을 사용자에게 보장할 수 있습니다.
장기적으로 이 ZK 책임 증명의 사용은 거래소 의 사용자 예금에만 국한되지 않고 더 넓은 범위의 대출 시나리오에서도 사용될 수 있습니다. 대출을 받은 사람은 누구나 해당 대출을 포함하는 다항식이나 트리에 기록을 넣고 루트는 온체인 에 게시됩니다. 이를 통해 대출을 원하는 사람은 누구나 대출 기관에 영지식 증명을 제공하여 다른 대출을 많이 받지 않았음을 보여줄 수 있습니다. 결국 법적 혁신을 통해 이러한 방식으로 약속된 대출이 미확정 대출보다 더 높은 우선순위를 갖도록 허용할 수도 있습니다. 이는 "탈중앙화 사회: Web3의 영혼 검색"에서 논의한 아이디어와 일치합니다. "영혼에 묶인 토큰"의 어떤 형태를 통해 온체인 부정적인 평판 개념이 가능해졌습니다.
자산 증명
자산 증명의 가장 간단한 버전은 위에서 본 프로토콜입니다. X 토큰을 보유하고 있음을 증명하려면 미리 결정된 시간에 X 토큰을 이동하거나 거래에서 "이 자금은 바이낸스에 속합니다"라는 메시지를 전달하기만 하면 됩니다. 거래 수수료 지불을 피하기 위해 오프체인 메시지에 서명할 수 있습니다. 비트코인과 이더 모두 오프체인 서명 메시지에 대한 표준을 가지고 있습니다.
이 간단한 자산 증명 기술에는 두 가지 실질적인 문제가 있습니다.
● 콜드월렛 처리
● 담보 재사용
보안상의 이유로 대부분의 거래소 대부분의 사용자 자금을 콜드 지갑, 즉 거래를 수동으로 서명하고 인터넷으로 전송해야 하는 오프라인 컴퓨터에 저장합니다. 이 방법은 매우 일반적입니다. 개인 자금을 저장하는 데 사용한 콜드 지갑은 영구 오프라인 컴퓨터에 있었으며, 서명된 거래가 포함된 QR 코드를 생성한 다음 휴대폰으로 스캔했습니다. 막대한 자금으로 인해 거래소 에서 사용하는 보안 프로토콜은 더욱 복잡해지며, 종종 여러 장치에 걸친 다자간 계산이 포함되어 단일 장치가 해킹되어 키 유출이 발생할 가능성을 더욱 줄입니다. 이러한 맥락에서 주소 제어를 증명하기 위해 추가 메시지를 생성하는 것조차 비용이 많이 드는 작업입니다!
거래소 다음 방법을 사용할 수 있습니다.
● 장기간 공개 주소를 유지합니다. 거래소 다수의 주소를 생성하고, 각 주소의 소유권 증명을 한 번만 발행한 후 해당 주소를 재사용합니다. 보안과 개인 정보 보호를 위해 몇 가지 제한 사항이 추가되기는 하지만 이는 가장 간단한 솔루션입니다.
● 다수의 주소를 보유하고 무작위로 다수의 주소를 인증합니다. 거래소 많은 주소를 보유하고 있으며 각 주소는 한 번만 사용될 수도 있으며 단일 거래 후에는 더 이상 사용되지 않을 수도 있습니다. 이 경우, 거래소 소유권을 증명하기 위해 거래소"개방"되어야 하는 일부 주소를 무작위로 선택하는 프로토콜이 필요합니다. 일부 거래소 이미 감사 와 유사한 운영을 수행하고 있지만 원칙적으로 이 기술은 완전히 자동화된 프로세스로 전환될 수 있습니다.
● 더욱 복잡한 ZKP 방법. 예를 들어, 거래소 모든 주소에 대해 1/2 다중 서명을 설정할 수 있습니다. 여기서 주소 중 하나는 다른 키를 갖고 다른 하나는 복잡하지만 안전한 방식으로 동일한 키를 갖습니다(예: 12/16 다중 서명). ) 중요한 비상 백업 블라인드 버전을 저장합니다. 개인 정보를 보호하고 전체 주소 유출을 방지하기 위해 거래소 블록체인 온체인 영지식 증명을 실행하여 이 형식으로 온체인 주소의 총 잔액 증명할 수도 있습니다.
또 다른 주요 문제는 담보 재사용을 방지하는 것입니다. 거래소 준비금을 증명하기 위해 서로 담보를 앞뒤로 이동하는 것이 종종 쉬우므로 사실상 지급 불능 상태에서 벗어날 수 있습니다. 이상적으로는 지불 가능성 증명이 실시간으로 수행되어야 하며 매 블록마다 증명이 업데이트되어야 합니다. 이것이 실용적이지 않은 경우, 차선책은 매주 화요일 오후 2시(UTC 시간)에 교정 예약을 하는 등 교정을 위해 거래소 간에 고정된 시간을 조정하는 것입니다.
마지막 질문은: 법정 통화로 자산 증명을 할 수 있습니까? 거래소 암호화폐뿐만 아니라 은행 시스템 내 법정화폐도 보유합니다. 이에 대한 대답은 '예'입니다. 그러나 그러한 프로그램은 필연적으로 "명목화폐" 신뢰 모델에 의존하게 됩니다. 즉, 은행 자체가 잔액 인증할 수 있고, 감사 대조표를 인증할 수 있습니다. 명목 화폐는 암호화 방식으로 검증할 수 없다는 점을 고려하면 이는 프레임 내에서 가장 좋은 솔루션이며 여전히 수행할 가치가 있습니다.
또 다른 접근 방식은 엔터티 A와 엔터티 B를 분리하는 것입니다. A는 일부 자산을 기반으로 하는 스테이블코인인 USDC의 거래소 및 처리를 담당하고, B는 암호화폐와 기존 은행 시스템 간의 현금 유입 및 거래를 처리합니다. 유출, 이 경우 B는 USDC 자체입니다. USDC의 "부채"는 온체인 ERC20 토큰이므로 책임 증명을 "쉽게" 얻을 수 있으며 자산 증명 문제만 처리하면 됩니다.
플라즈마 및 유효성 검사: 관리되지 않는 CEX를 구현할 수 있나요?
한 단계 더 나아가고 싶다고 가정해 보겠습니다. 우리는 거래소 사용자에게 상환할 만큼 충분한 자금을 가지고 있다는 것만 증명하고 싶지 않습니다. 대신, 우리는 거래가 사용자 자금을 훔치는 것을 완전히 방지하고 싶습니다.
이를 가장 먼저 시도한 것은 2017년과 2018년 이더 연구 커뮤니티에서 인기를 끌었던 확장 솔루션인 플라즈마(Plasma)였습니다. 플라즈마는 잔액 독립적인 "토큰" 세트로 분할하여 작동하며, 각 토큰에는 인덱스가 할당되고 플라즈마 블록의 머클 트리의 특정 위치에 배치됩니다. 유효한 토큰 전송이 발생하려면 트랜잭션이 트리의 올바른 위치에 배치되어야 하며 트리의 루트가 온체인 에 게시됩니다.
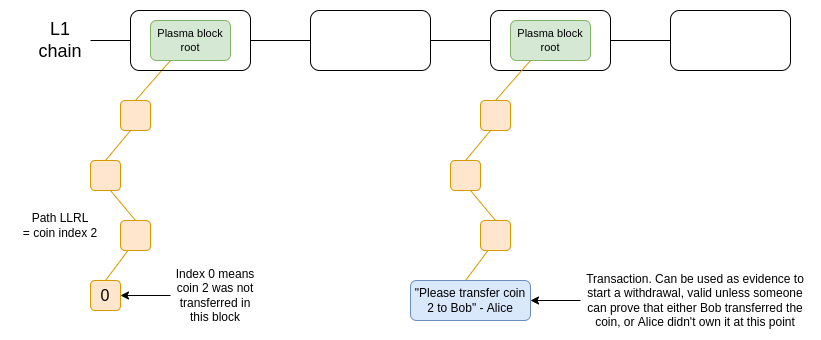
플라즈마 버전의 미니멀리스트 다이어그램. 토큰은 철회 시 플라즈마 프로토콜의 규칙을 시행하는 스마트 계약에 보관됩니다.
OmiseGo는 이 프로토콜을 기반으로 탈중앙화 거래소 만들려고 시도했지만 그 이후로 낙관적인 롤업 프로젝트인 Optimism을 통해 Plasma Group과 마찬가지로 다른 것으로 이동했습니다.
2018년 플라즈마의 한계에 대한 논의(동전 증명 조각 모음 등)는 모든 사람이 플라즈마의 타당성을 근본적으로 의심하게 만들었습니다. 플라즈마 논의가 2018년에 최고조에 달한 이후 ZK-SNARK는 확장 관련 사용 사례에 점점 더 적합해졌으며 위에서 말했듯이 ZK-SNARK는 모든 것을 변화시킵니다.
플라즈마의 업데이트된 버전은 Starkware가 validium이라고 부르는 것입니다. 데이터가 오프체인으로 유지된다는 점을 제외하면 기본적으로 ZK 롤업과 동일합니다. 이 구성은 많은 사용 사례에 적합하며 중앙 집중식 서버가 코드를 올바르게 실행하고 있음을 증명해야 하는 모든 시나리오에 적용될 수 있습니다. Validium에서는 운영자가 자금을 훔칠 수 없지만, 구현 세부 사항에 따라 운영자가 사라지면 일부 사용자 자금이 정체될 수 있습니다.
현재 상황은 좋아 보입니다. CEX와 DEX는 둘 중 하나와는 거리가 멀고, 효율성과 같은 몇 가지 이점을 얻을 수 있는 다양한 형태의 하이브리드 중앙 집중화를 포함하여 다양한 옵션이 있지만 여전히 많은 옵션이 있습니다. 암호화 학습 보호는 중앙 집중식 운영자에 의한 대부분의 악의적인 행동을 방지할 수 있습니다.
그러나 나머지 근본적인 질문은 사용자 오류를 처리하는 방법에 대해 생각해 볼 가치가 있습니다. 지금까지 가장 중요한 오류 유형은 다음과 같습니다. 사용자가 비밀번호를 잊어버리거나, 기기를 분실하거나, 해킹당하거나, 계정에 액세스할 수 없게 되면 어떻게 되나요?
거래소 이 문제를 해결할 수 있습니다. 먼저 이메일 복구를 활용하고, 실패하더라도 KYC를 통해 보다 복잡한 복구를 진행합니다. 하지만 이러한 문제를 해결하려면 거래소 실제로 이러한 토큰을 통제해야 합니다. 사용자 자금을 합리적으로 회수할 수 있으려면 거래소 이유 없이 사용자 자금을 훔치는 데 사용할 수 있는 것과 동일한 권한을 가져야 합니다. 이는 불가피한 절충안입니다.
이상적인 장기 솔루션은 사용자가 향후 다중 서명 및 소셜 복구 지갑과 같은 기술을 쉽게 사용하여 긴급 상황에 대처할 수 있는 자체 보관에 의존하는 것입니다. 단기적으로는 비용과 이점이 서로 다른 두 가지 확실한 대안이 있습니다.

또 다른 중요한 문제는 크로스 체인 지원입니다. 거래소 다양한 체인을 지원해야 하며, 플라즈마 및 유효성 검사와 같은 시스템은 다양한 플랫폼을 지원하기 위해 다양한 언어로 코딩되어야 하며 현재 형태로는 일부 플랫폼에서 사용할 수 없습니다. (특히 비트코인) 이는 기술 업그레이드와 표준화를 통해 해결될 것으로 예상되지만, 단기적으로 이는 오늘날의 보관 거래소 보관 모델을 유지해야 하는 또 다른 이유입니다.
결론: 앞으로 더 나은 거래소 기대합니다
단기적으로 거래소 에는 관리형 거래소 와 비수탁형 거래소 라는 두 가지 명확한 범주가 있습니다. 오늘날 후자의 범주는 Uniswap과 같은 DEX이며, 미래에는 사용자 자금이 validium 스마트 계약과 유사한 방식으로 보관되는 암호화 기반 CEX도 볼 수 있습니다. 우리는 암호화폐가 아닌 명목화폐 처리를 신뢰하는 준보관형 거래소 도 볼 수 있습니다.
두 가지 유형의 거래소 모두 존재하며, 보관 거래소 의 보안을 향상시키는 가장 쉬운 이전 버전과 호환되는 방법은 PoR준비금 증명 추가하는 것입니다. 여기에는 자산 증명과 부채 증명이 모두 포함됩니다. 두 가지 모두를 위한 좋은 프로토콜을 설계하는 데는 여전히 몇 가지 어려움이 있지만, 우리는 두 가지 유형의 기술을 함께 사용하고 가능한 경우 오픈 소스 소프트웨어와 프로그램을 추진하여 모든 거래소 이익을 얻을 수 있도록 추진할 수 있고 또 그래야 합니다.
장기적으로는 적어도 암호화폐의 경우 모든 거래소 비수탁형이 되는 상황으로 나아가기를 바랍니다. 지갑 복구가 존재하며 소규모 자금을 가진 신규 사용자와 법적인 이유로 그러한 준비가 필요한 기관을 위한 고도로 중앙 집중화된 복구 옵션이 필요할 수 있지만 이는 거래소 내에서가 아닌 지갑 계층에서 수행될 수 있습니다. 명목화폐의 경우 USDC와 같은 자산 기반 스테이블코인 고유의 자금 유입 및 유출 프로세스를 통해 전통적인 은행 시스템과 암호화폐 생태계 간의 이동이 완료될 수 있습니다. 그러나 아직 갈 길이 멀다.
[1] 번역자 주:➤ 16개의 숫자는 모두 사용자를 나타냅니다. (처음 15개의 숫자는 사용자의 잔액 나타내고, 마지막 숫자는 현재까지 사용자 잔액 과 명세서 간의 차액을 나타냅니다.) 위의 예는 두 명의 사용자를 나타낸다는 것을 알 수 있습니다(독자는 여기서 어느 정도 통찰력을 가질 수 있습니다).
➤ 청구된 평균 사용자 잔액: 185
➤ 사용자 1의 잔액: 20 -> 000 0000 0001 0100
차이: 20 – 185 = -165
➤ 사용자 2의 잔액: 50 -> 000 0101 0011 0010
차이: -165 + 50 -185 = -300
➤ 최종적으로 모든 사용자를 순회한 후 마지막 사용자의 차이 요구사항은 0입니다.
➤ 네 가지 방정식에 대한 설명
방정식 1: 재귀의 초기 값은 0입니다.
방정식 2: 각 사용자의 잔액 KZG 약속과 일치해야 합니다.
방정식 3: 각 사용자의 잔액 에 대한 재귀 공식, 제약 잔액>= 0 및 < 214
(잔액< 215라는 위의 진술은 공식 오류여야 합니다. 왜냐하면 방정식 3에 따르면 재귀 공식에는 I(zi) < 214라는 14개의 값만 있기 때문입니다.
16개의 숫자는 다음과 같습니다. I(z{16x+1}) | I(z{16x+14}) |
16개의 숫자는 최대값에 해당합니다: 0 | 21 -1| 214 -1|
방정식 4: 모든 사용자의 총 잔액 거래소 선언한 잔액 과 일치하도록 제한
이 기사 번역에 기여한 ECN 커뮤니티 번역 자원봉사자 @doublespending에게 특별히 감사드립니다.
면책조항: 블록체인 정보 플랫폼으로서 이 사이트에 게시된 기사는 작성자와 게스트의 개인적인 관점 만을 나타낼 뿐이며 Web3Caff의 입장과는 아무런 관련이 없습니다. 기사에 포함된 정보는 참고용일 뿐 어떠한 투자 조언이나 제안도 아닙니다. 귀하가 위치한 국가 또는 지역의 관련 법률 및 규정을 준수하시기 바랍니다.








