Aram Jivanyan, Albert Garreta, Hayk Hovhanissyan, Ignacio Manzur, Isaac Villalobos-Gutiérrez, Michal Zajac이 작성했습니다.
이 글에서는 많은 증명을 동시에 생산해야 할 때 비용을 상각하는 문제를 연구합니다. "패킹"이라고 부르는 이 방법은 FRI 기반 SNARK(예: ethSTARK, Plonky2, RISC0, Boojum 등)에 적용됩니다. 이 기법을 사용하면 검증자의 작업과 증명 크기를 줄이면서 많은 증인이 일부 제약 조건을 만족하는 단일 증명을 생성할 수 있습니다(각 증인에 대한 증명을 생성하고 검증자가 이를 각각 확인하는 것에 비해). 저희는 실험을 통해 이 기술이 실제로 유용하다는 것을 증명했습니다.
곧 발표될 기술 논문에서는 패킹 메커니즘에 대해 더 자세히 살펴보고, FRI 기반 SNARK 증명 작업을 통합하는 다른 방법에 대해 논의할 예정입니다. 이 작업은 SNARK 증명 작업의 누적 방법(예: 폴딩 방식)을 설계하기 위한 커뮤니티의 최근 노력을 이어가는 것으로 볼 수 있습니다. 그러나 FRI 기반 SNARK를 설정할 때는 동형 커미트먼트 스키마가 없다는 불편함에 직면하게 되는데, 이는 최근에 개발된 것과는 상당히 다른 접근 방식이 필요합니다.
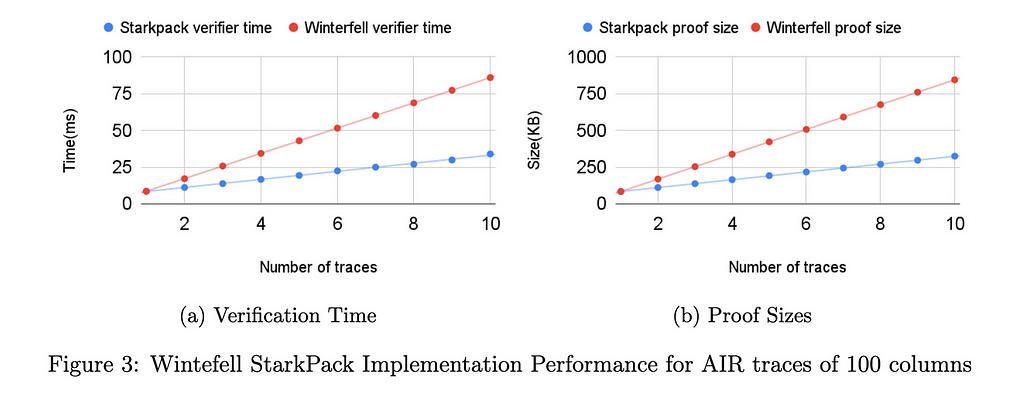
좀 더 자세히 설명하자면 패킹은 증명자가 잠재적으로 다른 인스턴스에 대한 증인의 만족도에 대한 단일 증명을 생성할 수 있는 일괄 증명 생성 방식입니다. 패킹의 주요 개선점은 증명자와 검증자가 모든 인스턴스에 대해 단 한 번의 FRI 저수준 테스트만 수행한다는 것입니다. 각 증인의 만족도를 순차적으로 증명하는 것에 비해 패킹된 증명의 검증자 시간과 증명 크기가 줄어들고, 증명자 시간은 약간 감소합니다. 저희의 벤치마크에 따르면 일반적인 트레이스(²¹⁶ 행, 100 열)의 경우 검증자 시간은 약 2배, 증명 크기는 약 3배 감소하는 것으로 나타났습니다.
나중에 설명하겠지만, 이 방법은 특히 긴 재귀 증명 작업과 함께 사용할 때 유용할 수 있습니다. 예를 들어, 단일 검증자가 여러 증인의 유효성에 대한 증명을 재귀적으로 생성하는 경우, 검증자는 "재귀적 레이어" 사이의 패킹을 사용하여 다음 레이어에서 더 작은 검증자와 더 작은 증인에 대한 진술을 증명할 수 있습니다.
패킹 방식은 잠재적으로 다른 관계와 유형의 FRI 기반 SNARK 증명에 대한 증명 작업을 "통합"할 수 있다는 점에 주목할 필요가 있습니다. 예를 들어 두 개의 언어 L₁, L₂와 두 개의 인스턴스 x₁, x₂의 경우, 패킹은 x₁∈L₁을 증명하는 데 드는 비용과 x₂∈L₂를 증명하는 데 드는 비용을 예를 들어 ethSTARK로 상각할 수 있습니다.
다음 섹션에서는 패킹 기법과 그 성능 개선에 대해 간략하게 살펴보겠습니다. 그 후, 몇 가지 잠재적 응용 사례에 대해 논의합니다. 그 다음에는 실험 결과를 제시합니다. 이 기법에 대한 공식적인 설명과 그에 따른 건전성 분석은 곧 발표될 기술 논문(추가 최적화 기법도 설명할 예정)으로 미루겠습니다.
개요
여기서는 특히 ethSTARK [Sta21] 프로토콜(STARK라고도 함)에 대한 접근 방식을 논의합니다. 그러나 이 기법은 모든 "FRI 기반 SNARK"([BGK+23]의 의미에서)에 적용할 수 있습니다. ethSTARK IOP는 아래의 청사진을 따른다는 점을 기억하세요. 아래에서 𝔽는 유한 필드를 나타내고, 𝕂는 𝔽의 유한 확장입니다.
- 증인은 오라클 함수 f₁, ..., fₛ입니다: D ⊂ 𝕂→ 𝕂, 특정 차수의 다항식으로 추정됩니다. 여기서 D는 곱셈 부분집합 D₀ ⊂ 𝔽*의 𝕂 내 코셋입니다. 이 코셋 D를 평가 영역이라고 합니다. 부분집합 D₀는 추적 영역 이라고 하는 크기 d+1의 부분집합 H₀=<g>를 포함합니다. 후자는 AIR 실행 트레이스의 행과 1-1로 대응합니다. 여기서 d는 차수 바운드입니다. 이를 fᵢ(X) 증인 맵이라고 부릅니다.
- 제약 조건은 함수 fᵢ(X)(및 일부 시프트 fᵢ(gʲ⋅X))의 다항식입니다. 이러한 각 다항식은 전체 트레이스 영역 H₀(또는 H₀의 부분 집합)에서 소멸해야 하지만, 단순화를 위해 모든 제약 조건이 모든 H₀에서 소멸한다고 가정해 보겠습니다.
- 예를 들어, 제약 조건은 Q(f₁(X), f₂(g⋅ X)) = f₁(X)² + f₂(f⋅ X)³의 형태를 가질 수 있습니다. 그렇다면 이 식은 H₀에서 소멸하는 "저차" 다항식으로, 모든 h∈ H₀에 대해 f₁(h)²=f₂(g⋅ h)³이 됩니다.
- 다음으로 검증자는 각 제약 조건의 무작위 선형 조합으로 단일 제약 조건 C: H → 𝕂를 생성하는 데 사용된 무작위성을 샘플링합니다. 우리는 C(X)를 DEEP-ALI 제약 조건이라고 부릅니다. 예를 들어 제약 조건이 Q₁(f₁(X), f₂(g⋅ X)) 및 Q₂(f₁(g²⋅ C), f₂(X))인 경우, 결합된 제약 조건은 맵 C(X) := Q(f₁(X), f₂(g⋅ X)) + α ⋅ Q₂(f₁(g²⋅ C), f₂(X))로, 여기서 α는 임의의 요소입니다. 이 제약 조건 역시 H₀에서 사라지는 저차 다항식으로 추정됩니다.
- 이제 증명자는 추적 영역 H₀의 소실 다항식인 Z(X)와 저차 다항식으로 가정되는 Z(X)에 의한 C(X)의 몫인 q(X)를 증명함으로써 C(X)가 위의 성질을 만족한다는 것을 증명할 수 있습니다. 이를 위해 증명자는 검증자에게 몫 맵 q(X)에 대한 오라클을 보냅니다. 그런 다음 다음과 같은 검사가 수행됩니다:
- 𝕂에서 샘플링된 단일 임의의 점 ξ(DEEP QUERY 점이라고 함)에서 C(X)=Z(X)⋅ q(X)가 유지되는지 확인합니다. 이를 확인하기 위해 증명자는 검증자에게 ξ와 시프트 gʲ⋅ ξ에서 각각 q_ξ와 {fᵢⱼ}로 느슨하게 표시되는 맵 q(X)와 {fᵢ(X)}의 평가를 전송합니다.
- 이제 검증자는 수신된 값이 올바른지, {fᵢ(X)}, q(X) 맵의 차수가 낮은지 확인해야 합니다. 이를 위해 증명자와 검증자는 Batch-FRI 프로토콜을 사용해 몫 (fᵢ(X)-fᵢⱼ)/(X-gʲ⋅ξ) 및 (V(X)-q_ξ)/(X-ξ)가 저차 다항식임을 증명합니다.
- Batch-FRI는 지도 h₁, ..., hₘ의 집합을 증명하는 데 사용되는 프로토콜이라는 것을 기억하세요: D\에서 𝔽까지가 차수 ≤ d의 다항식에 가깝다는 것을 증명하는 프로토콜입니다(보다 기술적으로, Batch-FRI는 이러한 맵이 리드-솔로몬 코드 RS[𝔽, D, d+1]에서 δ-상관 관계를 갖는다는 것을 증명합니다). 이 프로토콜은 지도 h₁, ..., hₘ의 무작위 선형 조합에 FRI 프로토콜을 적용하는 방식으로 작동합니다. 지도 (fᵢ(X)-fᵢⱼ)/(X-gʲ⋅ξ) 및 (V(X)-q_ξ)/(X-ξ)의 무작위 선형 조합을 DEEP-FRI 함수라고 부릅니다.
이 기법에서 주목할 점은 DEEP-ALI 제약 조건 조합과 Batch-FRI 조합의 선형성을 이용해 여러 인스턴스에 대한 증명 생성에 걸쳐 제약 조건과 함수를 하나의 결합된 제약 조건과 단일 DEEP-FRI 함수로 패킹할 수 있다는 것입니다. 즉, 여러 개의 ethSTARK 증명을 생성할 때 모든 개별 증명에서 모든 DEEP-ALI 제약 조건의 무작위 선형 조합을 취할 수 있습니다. 그런 다음, 증명자와 검증자는 위의 4단계를 실행하여 "글로벌" DEEP-ALI 컨스트레인트를 생성합니다.
Batch-FRI를 적용할 때는 일괄 처리된 맵의 평가 도메인 D에 대한 평가도 공개해야 합니다. 머클 커미트먼트로 인스턴스화할 때, 우리는 동일한 머클 리프의 D의 동일한 지점에 있는 증인 및 몫 맵의 모든 평가를 패킹합니다([MAGABMMT23]에서와 유사하게). 즉, 위의 표기법에 따라 머클 트리의 리프는 해시(h₁(a), ..., hₘ(a))처럼 보이며, 여기서 a∈D와 h₁, ..., hₘ는 증명에 투입되는 모든 증인 및 몫 맵입니다. 이는 Batch-FRI의 내부 라운드에서 머클 트리에는 적용되지 않는다는 점에 유의하세요.
아래에서는 N개의 인스턴스(Plonkish, AIR, RAP 인스턴스 등)에 대한 N개의 증인의 만족도를 위해, 각 인스턴스에 대해 순차적으로 FRI 기반 증명(Plonky2, ethSTARK, RISC0 등을 사용하여 생성할 수 있음)을 확인하는 검증자를 "순차 검증자"라고 부를 것입니다. "패킹된 검증자"는 각 증인의 동시 만족도를 위해 STARKPacked 증명을 확인하는 검증자를 지칭합니다. 증명자에게도 동일한 용어가 적용됩니다.
계산 개선
서로 다른 인스턴스의 만족도를 순차적으로 증명하는 것과는 반대로 개선된 점은 주로 머클 커미트먼트 트리의 수가 줄어들고 모든 인스턴스의 만족도에 대해 단 한 번의 FRI 증명만 수행한다는 사실에서 비롯됩니다. 첫 번째는 인스턴스 전반의 각 라운드에서 모든 관련 함수에 대한 평가를 동일한 머클 리프에 포함시키기 때문에 발생합니다. 앞서 설명했듯이 두 번째는 모든 몫 함수를 단일 DEEP-FRI 함수로 결합하기 때문에 발생합니다.
보다 구체적으로, 증명 크기 측면에서 보면, 순차 증명보다 머클 루트 커밋이 더 적게 포함됩니다. 또한 패킹된 모든 인스턴스에서 FRI를 한 번만 실행하기 때문에 머클 커밋 해제 경로도 더 적습니다. 그러나 패킹된 증명자가 전송해야 하는 함수 평가 횟수에 대한 상각은 없습니다.
패킹된 검증자 작업과 관련해서는 수행해야 하는 해시 연산 횟수가 줄어든다는 점에서 개선이 이루어집니다. 이는 패킹된 검증자가 확인해야 하는 머클 탈위임 증명의 수가 줄어든 데서 비롯됩니다. 더 구체적으로 설명하자면, 증인 함수와 몫 함수 q(X)를 포함하는 머클 트리의 경우, 패킹된 검증자는 머클 멤버십 증명을 확인하기 위해 더 큰 잎을 해시하지만, 그 수는 더 적습니다. 또한, 패킷화된 검증자는 FRI의 단일 실행에 해당하는 머클 분해 경로를 확인합니다.
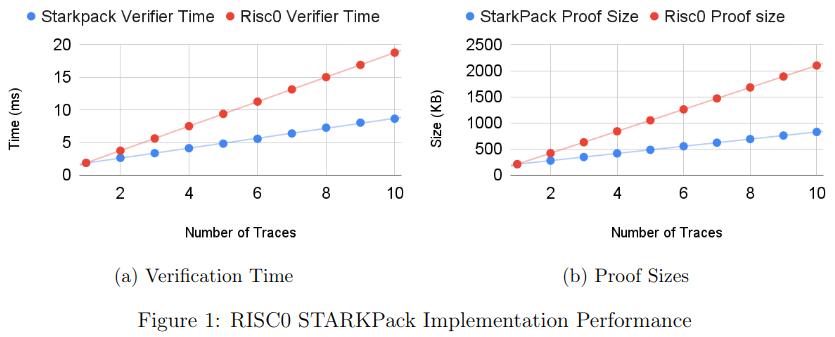
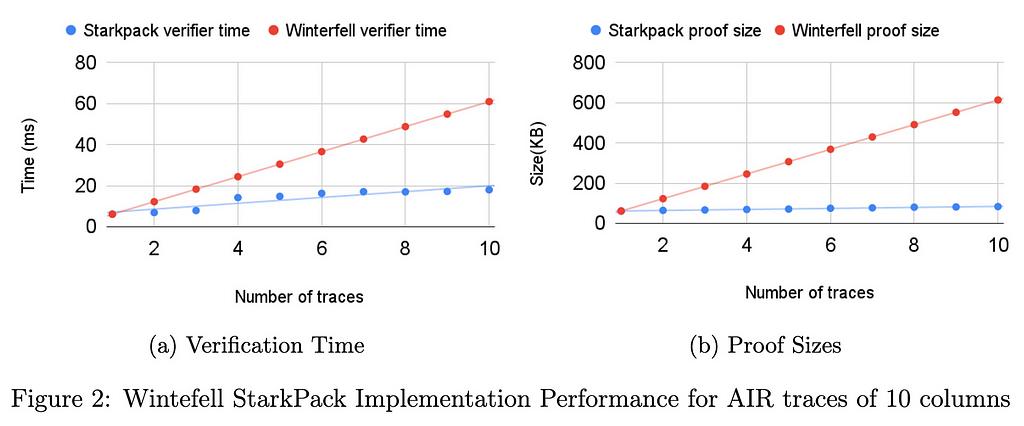
초기 벤치마크(성능 섹션 참조)에 따르면 ²¹⁶×100 크기의 트레이스의 경우 윈터펠로 모든 인스턴스의 만족도를 순차적으로 증명할 때보다 검증 시간과 증명 크기가 모두 절반 이상 줄어듭니다. RISC0에서는 트레이스의 열 수가 고정(275개)되어 있지만 검증자 시간과 증명 크기가 두 배로 개선된 효과가 여전히 적용됩니다. 물론 패킹 기법을 사용할 때 지불해야 하는 대가는 배치 함수 수가 증가함에 따라 프로토콜의 건전성이 저하된다는 것입니다. 곧 공개될 기술 문서에서는 구조의 건전성을 공식적으로 증명할 것입니다.
증인 함수와 몫 함수 q(X)를 포함하는 머클 트리의 경우, 트리의 첫 번째 레벨에 대한 머클 탈취 비용은 패킹 기법에 의해 상각되지 않는다는 점에 주목할 필요가 있습니다. 이는 앞서 설명한 것처럼 머클 트리의 잎이 이제 평가 벡터(패킹된 인스턴스당 하나씩)가 되고, 따라서 패킹된 인스턴스의 수 N에 따라 크기가 선형적으로 증가하기 때문입니다. 이는 실험에서 패킹된 검증기 작업이 트레이스 N의 수에 따라 대부분 선형적으로 확장되는 이유를 부분적으로 설명해줍니다.
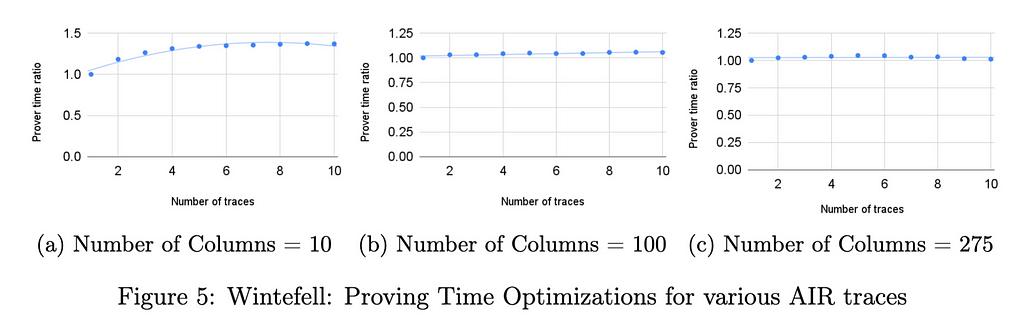
또한 이 기법이 검증자 시간을 줄이는 이유와 비슷한 이유로 증명자 시간도 줄여야 한다고 생각했습니다. 그러나 열과 패킹된 인스턴스의 수가 증가함에 따라 결합된 DEEP-ALI 제약 조건을 계산하는 데 필요한 필드 작업의 비용이 점점 더 중요해집니다. 실제로 우리 기법에서는 결합된 제약 조건 함수의 계산에 대한 상각이 없습니다. 이 비용은 일괄 처리하는 RAP(또는 AIR) 인스턴스의 열 수가 증가함에 따라 크게 증가합니다. 아래 표시된 벤치마크에서 이를 확인할 수 있는데, 열 수가 많을 경우(275개) 증명 시간이 약 5% 향상됩니다.
애플리케이션
아래에서 패킹 기법의 몇 가지 적용 사례를 살펴보겠습니다. 앞서 언급했듯이, 서로 다른 산술화에서 비롯된 인스턴스, 예를 들어 AIR 인스턴스와 터보플롱크(또는 플롱크와 유사한) 인스턴스의 동시 만족성에 대한 단일 증명을 생성할 수 있다는 점은 주목할 가치가 있습니다. 이는 각 산술화가 제공하는 트레이드오프와 롤업마다 다른 산술화를 사용하는 증명 시스템을 사용한다는 사실에 따라 흥미로울 수 있습니다. 또한, 이 패킹 기법은 다른 증명 시스템에 대한 증명을 패킹하는 데 쉽게 적용될 수 있습니다.
아래의 세 가지 애플리케이션은 모두 동일한 원리를 사용합니다. 즉, 스타크 재귀 증명 사이에 패킹 기법을 사용해 검증자 회로와 재귀 증인의 크기를 줄입니다. 따라서 재귀 증명 속도가 빨라집니다. 곧 발표될 기술 백서에서는 이 전략이 가져온 개선 사항에 대한 벤치마크를 제공할 예정입니다. 이는 최소한 다음 섹션에서 제공하는 간단한 초기 벤치마크만큼은 도움이 될 것입니다.
Zk-롤업: 스타크는 영지식 증명 기반 이더리움 확장 솔루션을 구축하는 저명한 블록체인 회사에서 zk-롤업이라는 이름으로 널리 사용되고 있습니다. 여기에는 스탁웨어, 폴리곤, zk싱크가 포함됩니다. 최근 zkSync는 부줌이라는 스타크 기반 L2 솔루션을 출시했고, 폴리곤은 폴리곤 미든을, 스타크웨어는 스타크넷을 배포했으며, 모두 비슷한 아키텍처를 따르고 있습니다. Polygon L2 플랫폼 설명[Tea22]에서 볼 수 있듯이, 레이어 2에서는 각 트랜잭션의 정확성이 독립적인 STARK 증명을 통해 증명되며, 모든 트랜잭션에 대한 STARK 증명은 독립적이지만 병렬로 생성됩니다. 나중에 이러한 독립적인 STARK 증명은 재귀적 증명 구성을 통해 병합됩니다. 그 결과 생성되는 일괄 증명은 재귀적 STARK 증명으로, 모든 입력 증명의 유효성을 보장합니다.
저희 기술은 먼저 패킹을 사용하여 수많은 독립 트랜잭션의 유효성에 대한 통합 증명을 생성함으로써 이 워크플로우를 최적화하여 검증할 증명을 더 작고 저렴하게 생성할 수 있습니다. 따라서 검증자 회로와 증인이 모두 작아지기 때문에 다음 재귀 반복은 증명자에게 더 저렴합니다. 이는 더 많은 재귀 계층에서도 반복될 수 있습니다.
배치 프로버: 스탁넷은 오프체인에서 카이로 연산 프로그램의 배치를 처리하고, 솔리디티 검증자 콘트랙트를 통해 온체인에서 증명을 검증하도록 설계된 공유 증명 시스템인 샤프(SHARP)를 도입했습니다. 쉐어드 프로그램 검증 비용은 다항식이기 때문에 여러 사용자가 제출한 다양한 카이로 프로그램을 하나의 증명으로 일괄 검증할 수 있으며, 모든 프로그램에 검증 비용을 효과적으로 분배할 수 있습니다. SHARP의 최신 버전은 각 프로그램이 도착할 때마다 처음에 개별적으로 증명하는 재귀적 증명을 통합합니다. 그런 다음 이러한 개별 증명은 점진적으로 재귀 증명으로 병합됩니다. 이 과정은 최종 증명이 온체인 검증자 컨트랙트에 제출될 준비가 될 때까지 계속됩니다. 저희가 제안하는 방법은 샤프의 재귀적 증명의 효율성을 높이는 것을 목표로 합니다. 각 프로그램을 개별적으로 증명하는 대신, 나중에 재귀 증명자가 입력하는 과정의 일부가 되는 패킹 인수를 사용하면 여러 문을 동시에 묶어 증명할 수 있어 보다 간결하고 빠르게 증명을 검증할 수 있습니다. 이는 재귀적 증명을 생성하는 데 드는 비용을 낮출 수 있습니다.
이더리움 단일 슬롯 완결성: 이더리움 재단은 최근 단일 슬롯 완결성 합의 시스템을 구축하기 위한 기본 아이디어[KKZM23]를 발표했습니다. 이 노트에서는 개념적으로 다른 두 가지 트리 기반과 가십 기반 서명 집계 토폴로지에 대해 설명하며, 두 가지 모두 효율적인 서명 집계 기법에 의존합니다. 집계 방식을 사용하면 여러 서명을 하나로 결합할 수 있으며 참여하는 모든 서명자의 신원을 추적할 수 있습니다. 이 사용 사례의 어려운 점은 각 참여자가 집계 프로세스에 두 번 이상 나타날 수 있다는 것입니다. BLS와 같이 효율적인 집계를 가능하게 하는 잘 알려진 서명 체계가 있지만, 각 서명자가 집계 프로세스에 여러 번 나타날 수 있는 경우 모든 서명자를 추적하는 것은 통신 복잡성에서 여전히 어려운 문제입니다. 이 노트에서는 영지식 암호화를 통해 이 문제를 효율적으로 해결하고자 하는 서명 병합이라는 새로운 개념에 대해 설명합니다. 서명 병합 체계를 인스턴스화하기 위해 제안된 접근 방식 중 하나는 재귀적 STARK를 기반으로 합니다. 재귀적 STARK는 계산에 다른 STARK 증명의 검증이 포함되며, 이는 다시 제공된 비트필드와 관련된 집계된 서명의 정확성을 검증한다는 점에서 특별합니다. 그 결과 재귀적 STARK 증명은 들어오는 증명이 유효하고 비트필드의 합이 주장된 결과와 같다는 것을 보장합니다. 서명 병합을 위한 재귀적 STARK의 제한 요소 중 하나는 [KKZM23]에서 설명한 것처럼 증명의 크기입니다. 이것이 바로 최종 증명을 재귀적으로 생성하기 전에 먼저 독립적인 STARK 증명에 대해 패킹 증명 통합 기법을 활용할 수 있는 시나리오입니다. 다시 말하지만, 재귀의 모든 계층에서 동일한 아이디어를 적용할 수 있으며, 이 접근 방식은 전반적으로 계산 비용이 더 저렴할 수 있습니다.
벤치마크
저희는 이 패킹 기법을 Winterfell과 RISC0 STARK 라이브러리에 구현했습니다. 윈터펠은 임의의 트레이스를 작성할 수 있고 트레이스를 최적화하는 데 뛰어난 유연성을 제공합니다. RISC0 아키텍처는 모든 트레이스가 프로그램과 관계없이 고정된 수(275개)의 열을 갖도록 AIR의 특정 구조 요소를 수정합니다. 컬럼 수는 최종 배치 증명 및 검증 성능에 중요한 역할을 합니다.
두 라이브러리에서 서로 다른 벤치마크를 실행했습니다. 모든 벤치마크에서 행의 수는 ²¹⁶로 고정되어 있습니다. 윈터펠에서는 각 열에서 i=1부터 i=²¹⁶까지 x_{i+1} = x_i³ + 42의 전이를 계산하는 회로의 경우 열의 수가 10에서 275까지 다양합니다. RISC0에서는 숫자의 두 소인수를 알고 있음을 증명하는 회로의 열이 275개로 고정되어 있습니다. 모든 테스트는 32GB RAM이 장착된 인텔 i712700F 컴퓨터에서 실행되었습니다. 벤치마킹한 인스턴스의 증명 시간 가속도는 약 5%였습니다. 증명 시간에서 이렇게 미미한 최적화 효과는 열의 수가 많기 때문입니다. 아래에 설명된 열 수가 적은 트레이스에 대한 윈터펠 벤치마크는 증명 시간 최적화가 열 수에 따라 어떻게 달라지는지 보여줍니다.
아래 다이어그램은 275개 컬럼의 AIR 트레이스에 대해 RISC0에서 구현된 StarkPack 성능 개선과 10개, 100개, 275개 컬럼의 트레이스에 대해 Winterfell에서 구현된 성능 개선을 보여줍니다.
결론
이 게시물은 초기 벤치마크에서 입증된 검증 복잡성 및 증명 크기의 개선을 강조하면서 FRI 기반 SNARK의 집계 방법에 대한 개략적인 요약을 제공하기 위해 작성되었습니다. 건전성 분석과 함께 이 방법과 추가 기술에 대한 포괄적인 설명은 기술 문서에서 확인할 수 있습니다.
참고 문헌
[BGK+23] 알렉산더 R. 블록, 알버트 가레타, 조나단 카츠, 저스틴 탈러, 프라티쉬 란잔 티와리, 미하우 자조크. 피아트-샤미르 보안 및 관련 스나크. 암호학 전자 인쇄 아카이브, 논문 2023/1071, 2023, https://eprint.iacr.org/2023/1071.
[BSCI+20] 엘리 벤 사손, 댄 카몬, 유발 이사이, 스와스틱 코파티, 슈브항기 사라프. 리드-솔로몬 코드의 근접 갭. 암호학 전자 인쇄 아카이브, 논문 2020/654, 2020. https://eprint.iacr.org/2020/654.
[KKZM23] 조지 카디아나키스, 드미트리 코브라토비치, 젠페이 장, 메리 말러. 대규모 합의를 위한 서명 병합, 2023. https://ethresear.ch/t/signature-merging-for-large-scale-consensus/17386.
[KST21] 아비람 코타팔리, 스리나스 세티, 이오안나 치알라. Nova: 폴딩 체계의 재귀적 영지식 인수. 암호학 전자 인쇄 아카이브, 논문 2021/370, 2021. https://eprint.iacr.org/2021/370.
[MAGABMMT23] 헥터 마십-아르데볼, 마크 구즈만-알비올, 호르디 바일리나-멜레, 호세 루이스 무뇨스-타피아. 에스탁: 인수를 사용한 스타크 확장. 암호학 전자 인쇄 아카이브, 논문 2023/474, 2023. https://eprint.iacr.org/2023/474.
[Sta21] 스타크웨어. ethSTARK 문서. 암호학 전자 인쇄 아카이브, 논문 2021/582, 2021. https://eprint.iacr.org/2021/582.
[Tea22] PolygonZero Team. 폴리곤 미든, 2022. https://polygon.technology/polygon-miden.
네더마인드 리서치 소개
이더마인드 리서치는 암호화, 탈중앙화 금융(DeFi), 프로토콜 연구 분야를 통합하여 각 분야를 향상시키는 시너지를 창출합니다.
자세한 내용은 여기를 참조하세요:
https://www.nethermind.io/applied-cryptography

스타크팩: 더 짧은 증명과 더 빠른 검증을 위한 STARK 통합은 원래 Medium의 Nethermind.eth에 게시되었으며, 사람들은 이 이야기를 강조하고 응답하며 대화를 이어가고 있습니다.