Rò rỉ không hoạt động được tiết lộ

avatar
Ethereum Research
06-10
Bài viết này được dịch máy
Xem bản gốc

Ở đây chúng tôi tóm tắt bài viết trình bày phân tích lý thuyết đầu tiên về rò rỉ không hoạt động, được thiết kế để khôi phục quá trình hoàn thiện trong các lỗi mạng thảm khốc. Tác phẩm này được chấp nhận tại DSN2024.

TL;DR

  • Việc rò rỉ không hoạt động về bản chất là vấn đề đối với sự an toàn của giao thức. Nó ủng hộ việc hoàn thiện liên tục các khối ( tính sống động ) với cái giá phải trả là có các khối hoàn thiện xung đột ( an toàn ).
  • Sự hiện diện của các trình xác thực Byzantine -các trình xác thực đi chệch khỏi giao thức - có thể đẩy nhanh việc mất đi sự an toàn.

Chuỗi khối Ethereum PoS phấn đấu cho sự phát triển liên tục của chuỗi hoàn thiện. Do đó, giao thức khuyến khích người xác nhận tích cực hoàn thiện các khối. Rò rỉ không hoạt động là cơ chế được sử dụng để lấy lại tính hữu hạn. Cụ thể, rò rỉ không hoạt động được bắt đầu nếu một chuỗi chưa trải qua quá trình hoàn thiện trong bốn kỷ nguyên liên tiếp. Vụ rò rỉ không hoạt động xảy ra lần đầu tiên trên mạng chính vào tháng 5 năm 2023.

Phần giới thiệu hay về vụ rò rỉ không hoạt động đã có sẵn nhờ công trình xuất sắc của Ben Eddington tại đây (điều đã thúc đẩy công việc này). Chúng tôi chính thức hóa việc rò rỉ không hoạt động bắt đầu bằng điểm không hoạt động.

Điểm không hoạt động

Trong một lần rò rỉ không hoạt động, tại kỷ nguyên t t , điểm không hoạt động, I_i(t) I i ( t ) , của trình xác nhận i i là:

\begin{cases}I_i(t) = I_i(t-1)+4, \text{if $i$ không hoạt động ở kỷ nguyên $t$} \\I_i(t) = \max(I_i(t-1) -1, 0), \text{ ngược lại.}\end{cases}
{ I i ( t ) = I i ( t − 1 ) + 4 , nếu i không hoạt động ở kỷ nguyên t I i ( t ) = max ( I i ( t − 1 ) − 1 , 0 ) , ngược lại.

Do đó, điểm không hoạt động của trình xác nhận sẽ tăng thêm 4,4 nếu nó không hoạt động và giảm 1,1 nếu nó hoạt động. Điểm không hoạt động luôn dương và sẽ được sử dụng để trừng phạt người xác nhận trong quá trình rò rỉ không hoạt động.

Hình phạt không hoạt động

Đặt s_i(t) s i ( t ) đại diện cho phần sở hữu của trình xác nhận i i tại kỷ nguyên t t và đặt I_i(t) I i ( t ) biểu thị điểm không hoạt động của nó. Hình phạt ở mỗi kỷ nguyên t t là I_i(t-1)\cdot s_i(t-1)/2^{26} I i ( t − 1 ) ⋅ s i ( t − 1 ) / 2 26 . Do đó, diễn biến của cổ phần được thể hiện bằng:

s_i(t)=s_i(t-1)-\frac{I_i(t-1)\cdot s_i(t-1)}{2^{26}}.
s i ( t ) = s i ( t − 1 ) − I i ( t − 1 ) ⋅ s i ( t − 1 ) 2 26 .

Cổ phần trong thời gian rò rỉ không hoạt động

Trong công việc này, chúng tôi mô hình hóa hàm cổ phần s như một hàm liên tục và khả vi, mang lại phương trình vi phân sau:

s'(t)=-I(t)\cdot s(t)/2^{26}.
s ′ ( t ) = − I ( t ) ⋅ s ( t ) / 2 26 .

Với phương trình này, chúng tôi có thể xác định số tiền đặt cược của người xác thực theo thời gian bằng cách ấn định sự tiến triển của điểm không hoạt động của người đó. Và đó chính xác là những gì chúng tôi làm. Chúng tôi xác định hai loại hành vi: Hoạt động và Không hoạt động.

  • Trình xác thực đang hoạt động: chúng luôn hoạt động.
  • Trình xác nhận không hoạt động: chúng luôn không hoạt động.

Những người xác nhận có những hành vi này trải qua những diễn biến khác nhau về điểm số không hoạt động của họ: (a) Người xác thực đang hoạt động có điểm không hoạt động không đổi I(t)=0 I ( t ) = 0 ; (b) Điểm không hoạt động của người xác nhận không hoạt động tăng 4 mỗi kỷ nguyên, I(t)=4t I ( t ) = 4 t . Cổ phần của từng loại trình xác nhận trong thời gian rò rỉ không hoạt động:

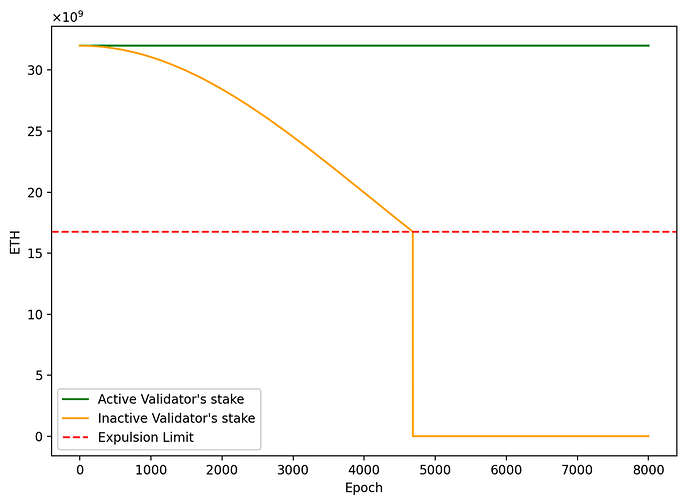
  • Cổ phần của người xác thực đang hoạt động: s(t) = s_0 = 32. s ( t ) = s 0 = 32.
  • Cổ phần của người xác thực không hoạt động: s(t) = s_0e^{-t^2/2^{25}}. s ( t ) = s 0 e − t 2 / 2 25 .
hình ảnh
hình ảnh 1472×1074 65,3 KB

Biểu đồ cho thấy sự phát triển về cổ phần của người xác nhận tùy thuộc vào hoạt động của họ trong thời gian rò rỉ không hoạt động. Giới hạn trục xuất được giao thức đặt ra để loại bỏ những người xác thực đã tích lũy quá nhiều hình phạt.

Trình xác thực đang hoạt động là gì?

Đây là một chi tiết quan trọng; hoạt động này thực sự phụ thuộc vào chuỗi. Điều này có nghĩa là các chuỗi khác nhau sẽ có điểm không hoạt động khác nhau đối với cùng một trình xác thực. Do đó, trình xác nhận có thể bị loại khỏi chuỗi và không làm mất wei trên chuỗi khác.

Đây là sự chính thức hóa của giao thức. Bây giờ chúng tôi thực hiện phân tích đặc tính an toàn của giao thức. Để làm như vậy, chúng tôi sử dụng mô hình sau.

Người mẫu

  • Mạng : Chúng tôi giả sử một hệ thống đồng bộ một phần, hệ thống này chuyển từ trạng thái không đồng bộ sang trạng thái đồng bộ sau Thời gian ổn định toàn cầu (GST) không xác định trước.
  • Lỗi : Trình xác thực là trung thực hoặc Byzantine (đi chệch khỏi giao thức). Trình xác nhận Byzantine có thể đi chệch khỏi giao thức một cách tùy ý.
  • Tiền đặt cược : Mỗi trình xác nhận bắt đầu với 32 ETH.

Không có giới hạn về độ trễ truyền tin nhắn trong trạng thái không đồng bộ.

Bị ràng buộc vì sự an toàn

Chỉ với những người xác nhận trung thực

Trong quá trình xây dựng, rò rỉ không hoạt động sẽ vi phạm an toàn nếu phân vùng xảy ra đủ lâu. Câu hỏi là, nhanh như thế nào?

Bất kỳ phân vùng mạng nào tồn tại lâu hơn 4686 kỷ nguyên (khoảng 3 tuần) sẽ dẫn đến mất An toàn do quá trình hoàn thiện xung đột. Đây là giới hạn trên về An toàn trong thời gian rò rỉ không hoạt động chỉ với những người xác nhận trung thực.

Phân tích chi tiết

Hãy để chúng tôi phân tích tình huống trong đó các trình xác nhận (tất cả đều trung thực) được chia thành hai. (Chúng tôi đang ở trạng thái không đồng bộ theo mô hình của chúng tôi).
Phân vùng nhất thiết sẽ tạo một nhánh, mỗi phân vùng xây dựng trên chuỗi duy nhất mà chúng nhìn thấy. Các chuỗi sẽ hoàn thiện sau khi tỷ lệ người xác thực đang hoạt động trở lại 2/3.

Trong trường hợp này, bằng cách hiểu sự phân bổ của người xác thực trên các phân vùng, chúng ta có thể tính toán thời gian cần thiết để tỷ lệ cổ phần của người xác thực đang hoạt động quay trở lại 2/3 số cổ phần trên mỗi nhánh, do đó hoàn tất và phá vỡ sự an toàn.

Để phân tích, chúng tôi thực hiện các ký hiệu sau. Khi bắt đầu rò rỉ không hoạt động:

  • n n là tổng số người xác nhận
  • n_B n B là tổng số trình xác thực Byzantine
  • n_H n H là tổng số người xác thực trung thực
  • n_{H_1} n H 1 là số lượng người xác thực trung thực trên nhánh 1
  • n_{H_2} n H 2 là số lượng người xác thực trung thực trên nhánh 2

Không có trình xác nhận Byzantine nào cho phần đầu tiên trong phân tích của chúng tôi, điều này ngụ ý rằng n=n_H n = n H . Trình xác thực trung thực chỉ được phân chia thành hai, do đó n_H=n_{H_1}+n_{H_2} n H = n H 1 + n H 2 .

Mục tiêu của chúng tôi là xác định khi nào tỷ lệ người xác thực trung thực ở nhánh 1 sẽ vượt trội hơn 2/3 tổng số cổ phần. Điều đó có nghĩa là chúng ta xem xét khi tỷ lệ:

\frac{\text{cổ phần của người xác thực ở nhánh 1}}{\text{cổ phần của người xác thực ở nhánh 1 + cổ phần của người xác thực ở nhánh 2}},
cổ phần của người xác thực ở nhánh 1 cổ phần của người xác thực ở nhánh 1 + cổ phần của người xác thực ở nhánh 2 ,

vượt trội hơn 2/3. Với ký hiệu của chúng tôi, tỷ lệ có thể được viết lại như sau:

\frac{n_{\text H_1}s_{\text H_1}(t)}{n_{\text H_1}s_{\text H_1}(t)+n_{\text H_2}s_{\text H_2}(t )} ,
n H 1 s H 1 ( t ) n H 1 s H 1 ( t ) + n H 2 s H 2 ( t ) ,

s_{\text H_1} s H 1 và s_{\text H_2} s H 2 lần lượt là tiền đặt cược của những người xác thực trung thực đang hoạt động và không hoạt động. Vì trình xác thực n_{\text H_1} n H 1 trên nhánh 1 luôn hoạt động trên nhánh 1 và trình xác thực n_{\text H_2} n H 2 luôn không hoạt động trên nhánh 1 (chúng hoạt động trên nhánh 2); chúng ta biết rằng s_{\text H_1}(t)=s_0 s H 1 ( t ) = s 0 và s_{\text H_2}(t)=s_0e^{-t^2/2^{25}} s H 2 ( t ) = s 0 e − t 2 / 2 25 .
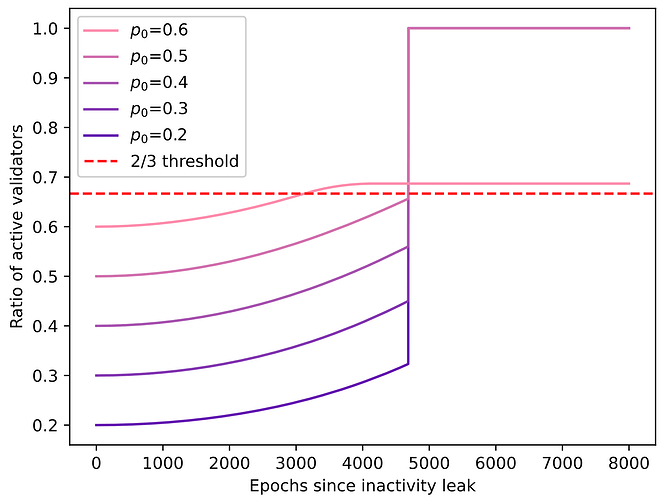
Sử dụng ký hiệu p_0=n_{\text H_1}/n_H p 0 = n H 1 / n H , tỷ lệ các trình xác nhận hoạt động theo thời gian là:

\frac{p_0}{p_0+(1-p_0)e^{-t^2/2^{25}}}.
p 0 p 0 + ( 1 − p 0 ) e − t 2 / 2 25 .
hình ảnh
hình ảnh 1972×1474 227 KB

Biểu đồ này hiển thị tỷ lệ trình xác thực đang hoạt động trên nhánh 1 theo thời gian. Nếu quá trình quyết toán không xảy ra trước epoch t=4685 t = 4685 , trình xác thực không hoạt động sẽ bị loại bỏ, khiến cho 100% trình xác thực đang hoạt động tăng vọt.

Trình xác nhận Byzantine

Bây giờ chúng tôi thêm trình xác nhận Byzantine.

Những trình xác nhận Byzantine này có thể gửi tin nhắn đến từng phân vùng mà không bị hạn chế.

Điều này có vẻ giống như sức mạnh quá mức, nhưng đây là giả định truyền thống trong các hệ thống phân tán để mang lại cho Byzantine nhiều sức mạnh hơn nữa. Bài báo của Gasper trình bày giao thức ETH2, đề cập nhiều đến bài báo PBFT trong mô hình của họ. Đây là một câu trong bài báo PBFT: “Chúng tôi cho phép một đối thủ rất mạnh có thể điều phối các nút bị lỗi, làm chậm quá trình liên lạc hoặc trì hoãn các nút chính xác để gây ra thiệt hại lớn nhất cho dịch vụ được sao chép”.
Giả định của chúng tôi kém mạnh mẽ hơn. Hãy tưởng tượng trường hợp một vách ngăn nơi liên lạc giữa Châu Âu và Châu Mỹ bị cắt đứt, nhưng liên lạc bên trong mỗi khu vực vẫn hoạt động. Theo mô hình của chúng tôi, chúng tôi giả định trình xác thực Byzantine có thể giao tiếp với cả hai khu vực mà không bị hạn chế như thể họ có cách giao tiếp riêng giữa các khu vực.

Tình hình chúng tôi phân tích bây giờ là như sau:

  • Chưa đến một phần ba cổ phần được nắm giữ bởi những người xác thực Byzantine ( \beta_0=n_{\rm B}/n<1/3 β 0 = n B / n < 1 / 3 ).
  • Người xác nhận trung thực được chia thành các nhánh 1 1 và 2 2 ; một tỷ lệ p_0=n_{\rm H_1}/n_{\rm H} p 0 = n H 1 / n H trên nhánh 1 1 và 1-p_0=n_{\rm H_2}/n_{\rm H} 1 − p 0 = n H 2 / n H trên nhánh 2 2 .
  • Trình xác thực Byzantine có thể giao tiếp với cả hai nhánh.

Trình xác thực Byzantine có thể hoạt động đồng thời trên cả hai nhánh, vi phạm an toàn nhanh hơn. Tỷ lệ trình xác nhận hoạt động trên nhánh 1 là:

\frac{p_0(1-\beta_0)+\beta_0}{p_0(1-\beta_0)+\beta_0+(1-p_0)(1-\beta_0)e^{-t^2/2^{25}} }.
p 0 ( 1 − β 0 ) + β 0 p 0 ( 1 − β 0 ) + β 0 + ( 1 − p 0 ) ( 1 − β 0 ) e − t 2 / 2 25 .

Bảng này hiển thị thời gian cần thiết để phá vỡ sự an toàn tùy thuộc vào tỷ lệ ban đầu của trình xác nhận Byzantine ( \beta_0 β 0 ):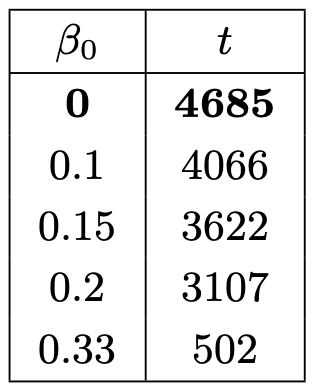
hình ảnh

Trình xác thực Byzantine có thể đẩy nhanh việc mất An toàn. Nếu tỷ lệ ban đầu của chúng là 0,33, thì chúng có thể khiến việc quyết toán xung đột diễn ra nhanh hơn khoảng mười lần so với các kịch bản chỉ liên quan đến những người tham gia trung thực.

Bài viết gốc cung cấp thêm chi tiết về các giả định, kịch bản, giao thức và các khía cạnh khác như:

  • Các cách để người xác thực Byzantine vi phạm sự an toàn mà không thực hiện hành vi có thể bị chém.
  • Các phương pháp để trình xác thực Byzantine vượt quá ngưỡng 1/3 trên cả hai nhánh của nhánh fork.
  • Một phân tích về cuộc tấn công nảy lên theo xác suất trong khi xem xét rò rỉ không hoạt động. Cảnh báo spoiler: điều này làm cho cuộc tấn công trở nên trầm trọng hơn một chút, nhưng các điều kiện để cuộc tấn công bắt đầu và tồn tại kịp thời khiến cho cuộc tấn công khó có thể trở thành một mối đe dọa thực sự.

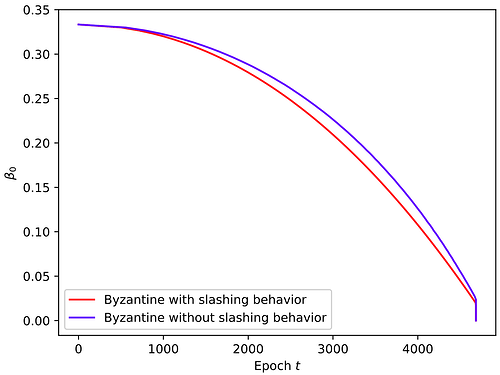
Để xem nhanh hơn các phát hiện của bài báo, đây là hình ảnh trình bày mức độ nhanh chóng mà các trình xác nhận Byzantine có thể phá vỡ sự an toàn tùy thuộc vào tỷ lệ ban đầu của chúng và liệu hành vi của chúng có thể bị cắt hay không. Như bạn có thể thấy, chúng có thể có tác động mạnh mẽ ngay cả khi không có hành vi có thể chém được.

hình ảnh
hình ảnh 1456×1090 72,4 KB

Phần kết luận

Phát hiện của chúng tôi nhấn mạnh tầm quan trọng của cơ chế xử phạt trong phân tích Dung sai lỗi Byzantine (BFT). Bằng cách xác định các vấn đề tiềm ẩn trong thiết kế giao thức, chúng tôi mong muốn cung cấp thông tin chi tiết về các cải tiến trong tương lai và các công cụ để điều tra thêm.

Khu vực:
SEC Security Token
Token Sàn Tập Trung (CEX)
Layer 1
Nguồn
Tuyên bố từ chối trách nhiệm: Nội dung trên chỉ là ý kiến của tác giả, không đại diện cho bất kỳ lập trường nào của Followin, không nhằm mục đích và sẽ không được hiểu hay hiểu là lời khuyên đầu tư từ Followin.
Thích
1
Thêm vào Yêu thích
Bình luận
Nội dung liên quan