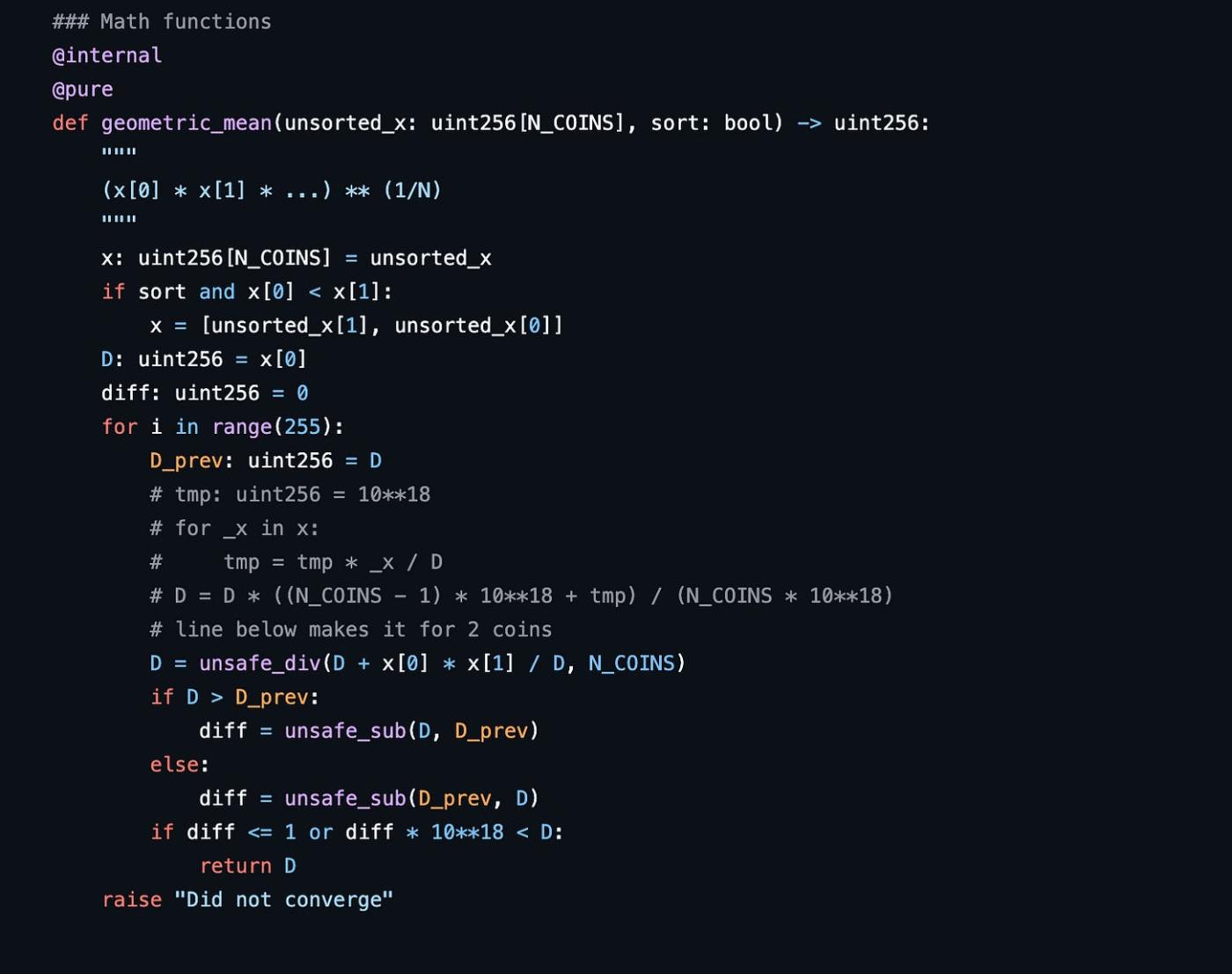
Phần thứ hai của bài viết này là về Bonding Curve của StableSwap.

CryptoSwap

Bonding Curve của CryptoSwap là một công thức toán học cốt lõi định nghĩa "đường cong thanh khoản" cho các nhóm giao dịch của Curve, được thiết kế đặc biệt cho các cặp tài sản biến động mạnh (không neo chặt như stablecoin). Nó giúp nhóm tập trung thanh khoản xung quanh một "giá nội bộ" (được xác định thông qua một oracle nội bộ) và tự động điều chỉnh khi nhóm trở nên mất cân bằng. Dưới đây là các điểm chính:

Kết hợp các ưu điểm của hai Bonding Curve:

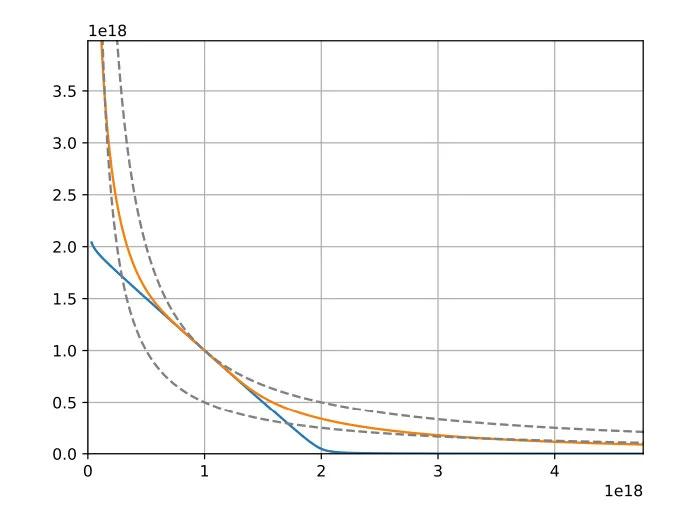
• Khi nhóm cân bằng (số dư tương đương về giá trị), Bonding Curve của CryptoSwap hoạt động tương tự như Bonding Curve của StableSwap, tạo ra một vùng "bằng phẳng" (không Slippage) cho phép trao đổi gần 1:1.

• Khi nhóm trở nên mất cân bằng, Bonding Curve sẽ dần chuyển sang hành vi của Bonding Curve sản phẩm hằng số (như Uniswap), dẫn đến Slippage tăng lên và bảo vệ nhóm khỏi các độ lệch giá quá mức.

Trong Phần 1, Bonding Curve của StableSwap được mô tả trong công thức chung:

Và Bonding Curve của CryptoSwap được khuyến khích bởi Bonding Curve của StableSwap:

tuy nhiên, K được định nghĩa hơi khác:

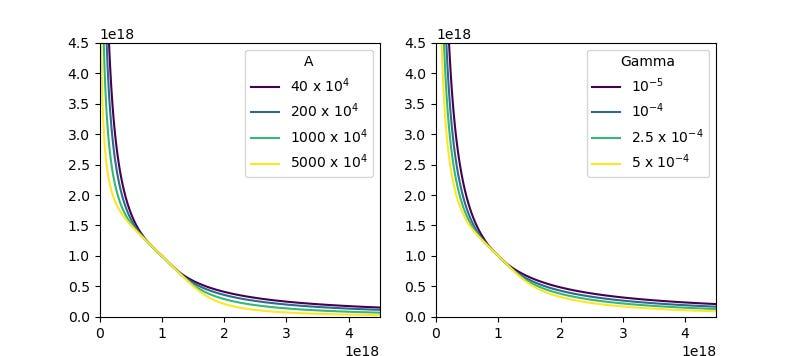
• A (hệ số khuếch đại): Tham số A, tương tự như Bonding Curve của StableSwap (Curve v1), kiểm soát độ bằng phẳng của Bonding Curve ở trung tâm. Điều này quyết định mức độ tập trung thanh khoản xung quanh tỷ giá trao đổi dự kiến (tức là "thang giá")

• Gamma: Tham số gamma kiểm soát khoảng cách giữa hai đường cong sản phẩm hằng số được hiển thị trong hình trên (đường nét đứt). Khi gamma tăng lên, nó kéo dài "đường cong sản phẩm hằng số đã điều chỉnh" về góc dưới bên trái, di chuyển các đường tiệm cận của đường cong gần các trục hơn và làm rộng hình dạng tổng thể của đường cong
  

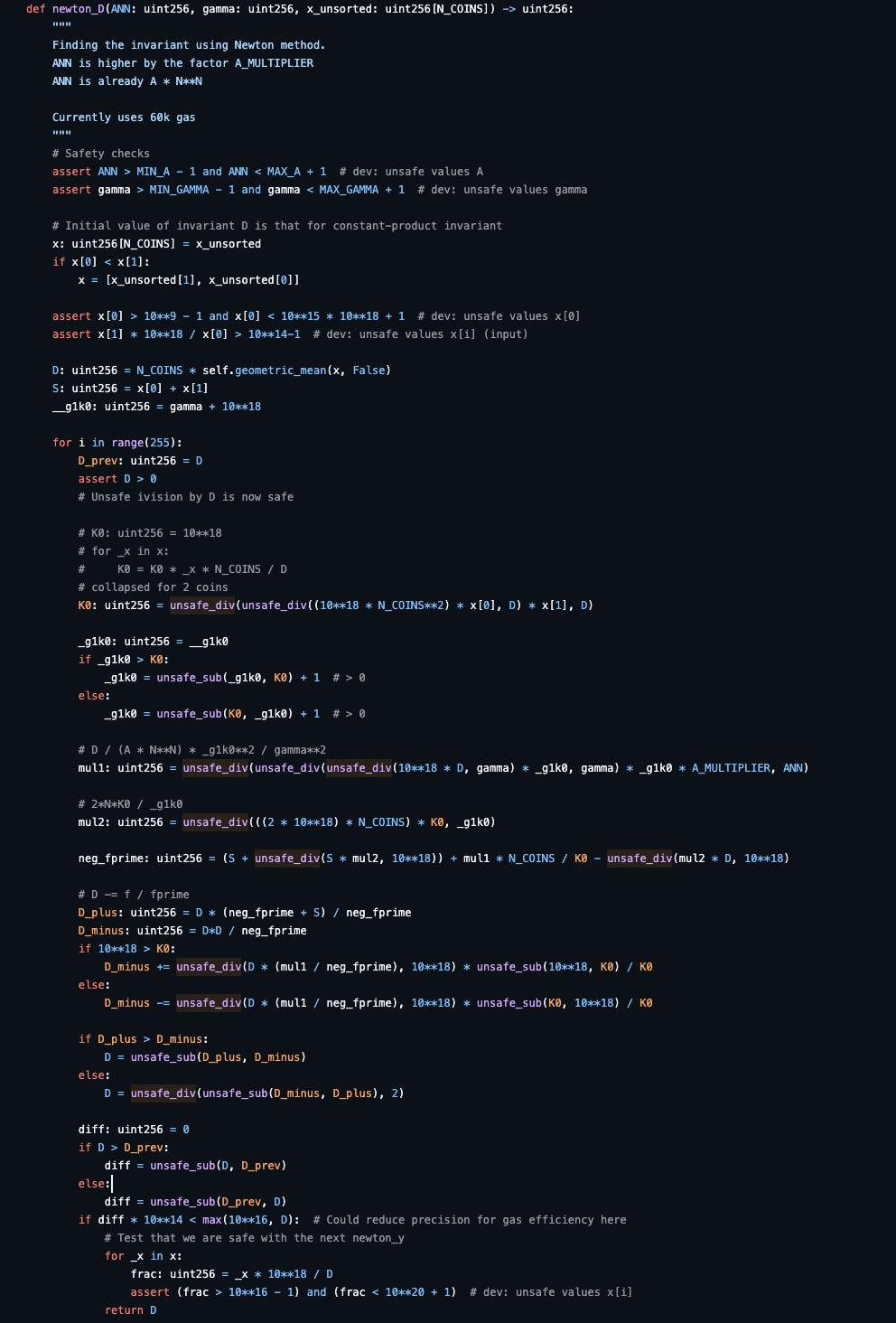
Khởi tạo:

Với công thức ban đầu, chúng ta có thể viết lại f(D_0) trong tình huống chỉ có 2 đồng tiền:

Sử dụng phương pháp Newton, các giá trị ban đầu có thể được chuyển đổi thành:

Với công thức này, D_0 có thể được tính bằng cách lặp lại A lần. Trong mã Viper, A được đặt thành 255.

Mã tính toán độ chênh lệch tuyệt đối giữa giá trị D_0 hiện tại và trước đó. Nó dừng lặp lại khi độ chênh lệch rất nhỏ (diff ≤ 1) hoặc khi độ chênh lệch nhân với 10^18 nhỏ hơn D_0. Một khi một trong những điều kiện này được đáp ứng, hàm sẽ trả về giá trị D_0 đã hội tụ.

Quay lại Bonding Curve, hãy để S là tổng của x_i và P là tích của x_i. f(D) với 2 đồng tiền (N = 2) trở thành:

Đạo hàm của f(D) là:

Điều này có thể được chuyển đổi thành:

Công thức trên có thể được chuyển đổi để đơn giản hóa. Đầu tiên, chia tất cả các thuật ngữ cho K và mở rộng tất cả những gì ở trong dấu ngoặc.

Bây giờ S có thể được viết là - S + 2S:

Sau đó, tách các thuật ngữ chung giữa các nhóm chứa S và D.

Làm cho tất cả các mẫu số bên trong dấu ngoặc chung:

Giới thiệu hai biến phụ trợ, mul1 và mul2, để đơn giản hóa các biến trong hàm:

Đạo hàm f'(D) bây giờ có thể được rút gọn thành:

Trong mã Viper, biến _g1k0 được định nghĩa là:

Quay lại mã,

Mã này tính -f'(D) thay vì f'(D). Điều này làm cho bước Newton rõ ràng hơn. Ngoài ra, f(D) được chia cho K:

Phương pháp Newton đầy đủ cho D bây giờ là:

Công thức đã được tách thành hai phần cho phương pháp Newton:

Giá trị cuối cùng của D sẽ được tính là sự khác biệt giữa hai phương trình trên.