Tổng hợp chữ ký dựa trên mạng lưới
Đây là báo cáo chung của David Nevado, Dohoon Kim và Miha Stopar.
Trong Proof-of-Stake của Ethereum, chữ ký BLS được sử dụng để tổng hợp các chứng thực từ nhiều trình xác thực thành một chữ ký nhỏ gọn duy nhất. Tuy nhiên, BLS không an toàn lượng tử và trong tương lai hậu lượng tử, nó sẽ cần được thay thế. Một hướng triển vọng là tổng hợp dựa trên mạng lưới, chẳng hạn như Aggregating Falcon Signatures with LaBRADOR gần đây, khám phá cách tổng hợp hiệu quả các chữ ký Falcon hậu lượng tử trong khi vẫn duy trì kích thước nhỏ và xác minh nhanh.
Trong khi LaBRADOR cung cấp một cách tiếp cận đầy hứa hẹn để tổng hợp các chữ ký Falcon với các bằng chứng nhỏ gọn (~74 KB cho 10.000 chữ ký), thì vẫn còn những giải pháp thay thế sau lượng tử khác. Một là sử dụng STARK để chứng minh trong kiến thức bằng không rằng nhiều chữ ký dựa trên băm là hợp lệ. Những cách tiếp cận này thường dẫn đến kích thước bằng chứng lớn hơn —khoảng 300KB cho 10k chữ ký —nhưng được hưởng lợi từ thời gian xác minh nhanh hơn.
Khi kết thúc bài viết này, chúng tôi so sánh phương pháp LaBRADOR với phương pháp tổng hợp chữ ký dựa trên băm gần đây. Trong lược đồ đó, chữ ký được khởi tạo bằng Poseidon2, trong khi tổng hợp dựa vào Keccak cho các lược đồ cam kết đa thức dựa trên cây Merkle. Bản thân tổng hợp bao gồm việc tính toán số học cho trình xác minh chữ ký trong hệ thống chứng minh theo kiểu Plonk.
LaBRADOR là một giao thức tương đối mới và hỗ trợ triển khai vẫn còn hạn chế. Mặc dù một số triển khai Rust đang nổi lên, nhưng chúng vẫn chưa sẵn sàng, do đó hiện tại, mã tham chiếu C gốc vẫn là tùy chọn chính. Để đánh giá chuẩn, chúng tôi đã sử dụng tập lệnh agg_sig.py từ kho lưu trữ Lazer, tập lệnh này bao bọc triển khai LaBRADOR C. Dưới đây, trước tiên chúng tôi trình bày một số kết quả đánh giá chuẩn, sau đó giải thích cách tiếp cận của Lazer khác với cách tiếp cận được mô tả trong bài báo gốc, Aggregating Falcon Signatures with LaBRADOR như thế nào.
Kết quả thực hiện
Tiếp cận :
Chúng tôi đã sử dụng nhánh LaBRADOR của mình, bao gồm các sửa đổi để hỗ trợ các lô chữ ký lớn hơn (vượt quá 2.000 chữ ký). Các sửa đổi được thực hiện để có thể tăng mô-đun lên khoảng 2^{48} 2 48 để xử lý các giá trị trung gian lớn hơn phát sinh trong quá trình tổng hợp.
Kết quả :
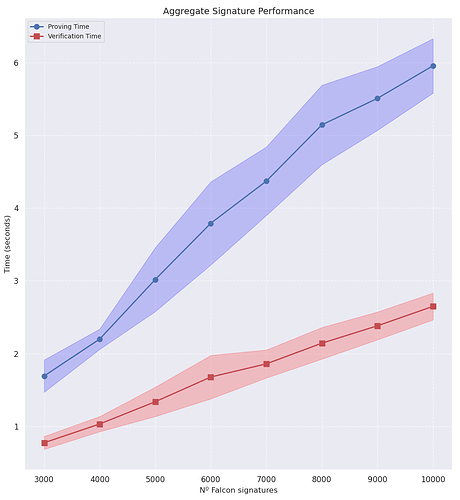
Chúng tôi đã đo thời gian chứng minh cho việc tổng hợp các lô từ 3.000 đến 10.000 chữ ký Falcon-512. Điểm chuẩn được lấy bằng cách thực hiện luồng đơn trên bộ xử lý 11th Gen Intel(R) Core(TM) i5-11400H @ 2.70GHz .
| # Chữ ký | Thời gian chứng minh (giây) | Thời gian xác minh (giây) | Kích thước bản in thử |
|---|---|---|---|
| 3000 | 1,6921 ± 0,2220 | 0,7739 ± 0,0888 | 77,83KB |
| 4000 | 2,1991 ± 0,1403 | 1,0321 ± 0,1044 | 69,82KB |
| 5000 | 3,0182 ± 0,4394 | 1,3380 ± 0,2021 | 72,45KB |
| 6000 | 3,7914 ± 0,5716 | 1,6779 ± 0,2989 | 72,11KB |
| 7000 | 4,3709 ± 0,4716 | 1,8586 ± 0,1928 | 71,83KB |
| 8000 | 5,1447 ± 0,5469 | 2,1430 ± 0,2175 | 74,02KB |
| 9000 | 5,5085 ± 0,4382 | 2,3821 ± 0,1915 | 72,27KB |
| 10000 | 5,9565 ± 0,3750 | 2,6492 ± 0,1848 | 74,07KB |
Lưu ý : Mặc dù không được hiển thị trong biểu đồ, cấu hình này hỗ trợ các lô chữ ký lớn hơn nữa. Các lô nhỏ hơn (<2.000 chữ ký) đạt hiệu suất tốt hơn vì mô đun có thể giảm xuống còn 2^{40} 2 40 , giảm thời gian chứng minh/xác minh và kích thước chứng minh.
Điểm chính :
10k chữ ký Falcon-512 có thể được tổng hợp với LaBRADOR dẫn đến:
- Kích thước bản in thử 74,07KB .
- Tạo bản kiểm tra trong 5,95 giây .
- Xác minh bằng chứng trong 2,65 giây .
Từ những kết quả này, thời gian xác minh nổi lên là rào cản lớn nhất đối với việc áp dụng. Chúng tôi đã phân tích xác minh để cải thiện hiệu suất của nó.
Phân tích xác minh
Việc tổng hợp các chữ ký Falcon được thực hiện bằng cách sử dụng một bằng chứng đóng gói và giao diện Dachshund (xem bài báo Lazer để biết mô tả ngắn gọn về Dachshund) được cung cấp trong thư viện LaBRADOR. Chúng tôi đã lập hồ sơ quy trình xác minh trong bài kiểm tra Dachshund để xác định các nút thắt và cơ hội tối ưu hóa tiềm năng. Mặc dù chúng tôi đã cố gắng cải thiện thời gian xác minh ban đầu thông qua song song hóa, nhưng những nỗ lực này đã không thành công.
Phân tích
Việc xác minh bản in thử được đóng gói mất 1.2510 giây và diễn ra trong composite_verify_simple , bao gồm hai bước:
- simple_reduce : Trích xuất câu lệnh hợp thành gốc
tsttừ câu lệnh đơnstvà chứng minhp(1,1356 giây, ~90% tổng thời gian). - composite_verify : Xác minh
pso vớitst(10% còn lại).
Với sự thống trị của nó, chúng tôi tập trung vào việc tối ưu hóa simple_reduce .
phân tích simple_reduce
Với mô-đun 48 bit, hằng số LIFTS = 3 Vòng lặp LIFTS chiếm 77% thời gian chạy , nhưng sự phụ thuộc tuần tự của nó (do thách thức của Fiat-Shamir) ngăn cản việc song song hóa.
| Chức năng | Thời gian (giây) | % Tổng thời gian chạy |
|---|---|---|
init_statement() + betasq | 0,0000 | 0,00% |
reduce_simple_commit() | 0,0000 | 0,00% |
reduce_project() | 0,0451 | 3,97% |
init_constraint() | 0,0000 | 0,00% |
| Vòng lặp LIFTS (3x) | 0,8800 | 77,50% |
free_constraint() + dọn dẹp | 0,0016 | 0,14% |
simple_aggregate() | 0,1067 | 9,40% |
aggregate_sparsecnst() | 0,0969 | 8,53% |
reduce_amortize() | 0,0053 | 0,47% |
| Tổng cộng | 1.1356 | 100% |
Trong vòng lặp, chúng tôi tìm thấy một số hàm là ứng cử viên cho việc tối ưu hóa. Đặc biệt là collaps_jlproj_raw() .
Phân tích vòng lặp LIFTS (mỗi lần lặp)
| Chức năng | Thời gian trung bình (giây) | % Tổng thời gian chạy |
|---|---|---|
collaps_jlproj_raw() | 0,1166 | 10,27% |
polxvec_setzero() | 0,0178 | 1,57% |
simple_collaps() | 0,0537 | 4,73% |
reduce_lift_aggregate_zqcnst | 0,1053 | 9,27% |
| Tổng cộng (mỗi lần lặp lại) | 0,2934 | 25,84% |
| Tổng cộng (3 lần lặp lại) | 0,8802 | 77,51% |
Các nỗ lực tối ưu hóa
LaBRADOR được tối ưu hóa mạnh mẽ với các lệnh AVX-512 nhưng vẫn là luồng đơn. Chúng tôi đã khám phá song song hóa nhưng gặp phải những thách thức:
Sự phụ thuộc của Fiat-Shamir :
Việc đưa ra các thách thức FS không thể tránh khỏi là theo trình tự và điều này hạn chế các cơ hội song song hóa.Các phép toán ma trận :
Việc song song hóapolxvec_jlproj_collapsmat(30% củasimple_reduce) với OpenMP làm giảm hiệu suất , có thể là do:- Chia sẻ sai (tranh chấp luồng cho các dòng bộ đệm).
- Độ bão hòa băng thông bộ nhớ (AVX-512 đã đạt băng thông tối đa).
Tuy nhiên, cần phải phân tích sâu hơn để xác định nguyên nhân gốc rễ.
So sánh: Lazer và Tổng hợp chữ ký Falcon với LaBRADOR
Thoạt nhìn, có vẻ như kỹ thuật Aggregating Falcon Signatures with LaBRADOR khá khác biệt so với kỹ thuật Lazer, nhưng thực tế không phải vậy.
Trước tiên, chúng ta hãy quan sát cách thức tổng hợp chữ ký Falcon hoạt động và sau đó tìm hiểu sâu hơn về sự khác biệt giữa hai phương pháp này.
Chữ ký chim ưng
Chữ ký Falcon bao gồm (s_1, s_2) ( s 1 , s 2 ) sao cho:
trong đó \mathbf{h} h là một phần của khóa công khai và \mathbf{t} t là hàm băm của một thông điệp.
Chúng tôi đang chứng minh kiến thức về \mathbf{s}_1 s 1 và \mathbf{s}_2 s 2 bằng một hệ thống chứng minh sử dụng một số modulo khác với q q , do đó phương trình được viết lại thành:
đối với một số đa thức \mathbf{v} v .
Tổng hợp các chữ ký Falcon
Chúng tôi muốn tổng hợp chữ ký N N Falcon, nghĩa là phải chứng minh:
với i=1,...,N. i = 1 , . . . , N .
Lưu ý rằng q q là môđun từ sơ đồ Falcon và phương trình cần phải giữ nguyên trong R_{q'} R q ′ trong đó q' > q q ′ > q , nhưng có cùng bậc vành đai d. d . Không được xuất hiện một phép bao quanh môđun q' q ′ trong phương trình để chứng minh rằng đẳng thức vẫn giữ nguyên trên R. R .
Bài báo Aggregating Falcon Signatures with LaBRADOR sử dụng LaBRADOR làm hệ thống chứng minh. Vào thời điểm bài báo được nộp, LaBRADOR không thể được sử dụng mà không có một số hạn chế bổ sung do các vấn đề chúng tôi mô tả bên dưới. Mã nguồn LaBRADOR—cùng với giao diện Dachshund—được phát hành sau đó và trên thực tế, giao diện Dachshund giải quyết trực tiếp các vấn đề ban đầu ngăn cản LaBRADOR được sử dụng như hiện trạng.
Vấn đề 1: kiểm tra chuẩn mực
Kiểm tra chuẩn sử dụng phép chiếu Johnson–Lindenstrauss trong LaBRADOR vừa gần đúng vừa áp dụng cho toàn bộ nhân chứng cùng một lúc. Cách tiếp cận này hiện được gọi là giao diện Chihuahua trong mã nguồn LaBRADOR. Ngược lại, giao diện Dachshund thực hiện kiểm tra chuẩn trên từng vectơ nhân chứng riêng lẻ. Nhớ lại từ trên rằng trong bối cảnh tổng hợp chữ ký, chúng ta có nhiều vectơ nhân chứng: \mathbf{s}_{i,1} s i , 1 và \mathbf{s}_{i,2} s i , 2 .
Vì Dachshund vẫn chưa được phát hành, bài báo được viết với giả định sử dụng giao diện Chihuahua. Giao diện này chứng minh rằng chuẩn mực của toàn bộ nhân chứng (tức là tất cả các vectơ nhân chứng kết hợp) là nhỏ—một cách tiếp cận phù hợp với một số ứng dụng nhất định.
Ý tưởng của phép chiếu Johnson–Lindenstrauss là sử dụng các ma trận chiếu ngẫu nhiên \Pi Π : đối với chứng \mathbf{s} s , phép chiếu \Pi \mathbf{s} Π s (phép nhân ma trận-vectơ) được tính toán và trình kiểm chứng trực tiếp tính chuẩn của vectơ chiếu. Có một bổ đề nêu, đại khái là, nếu phép chiếu nhỏ, thì vectơ gốc cũng nhỏ: nếu |\Pi \mathbf{s}|_2 \leq \sqrt{30} b | Π s | 2 ≤ √ 30 b đối với một số ràng buộc b b , thì |\mathbf{s}|_2 \leq b | s | 2 ≤ b . Nó cũng phải giữ nguyên rằng \sqrt{\lambda} b \leq \frac{q}{C_1} √ λ b ≤ q C 1 đối với mức độ bảo mật \lambda λ và một hằng số C_1 C 1 nào đó . Điều này áp đặt các ràng buộc lên mô đun q q được sử dụng trong lược đồ tổng hợp—một trong những lý do bài báo sử dụng mô đun lớn hơn q' > q q ′ > q thay vì mô đun q q ban đầu của Falcon.
Tuy nhiên, trong trường hợp tổng hợp chữ ký, cần phải chứng minh tính nhỏ của từng vectơ chứng kiến riêng lẻ—chẳng hạn như \mathbf{s}_{i,1} s i , 1 và $\mathbf{s}_{i,2}$—chính xác là những gì Dachshund được thiết kế để hỗ trợ. Vì Dachshund vẫn chưa có sẵn, nên các tác giả của bài báo đã đưa ra các ràng buộc rõ ràng bổ sung để áp dụng các giới hạn chuẩn trên các vectơ chứng kiến riêng lẻ. Phép chiếu Johnson–Lindenstrauss vẫn được sử dụng trong bài báo, nhưng cho một mục đích khác: để ngăn chặn việc bao quanh theo modulo. Chúng tôi tóm tắt các ràng buộc chuẩn rõ ràng và việc sử dụng phép chiếu Johnson–Lindenstrauss để ngăn chặn việc bao quanh theo modulo bên dưới.
Ràng buộc chuẩn vector chứng kiến cá nhân
Chứng minh rằng ||\mathbf{s}_{i,1}||^2_2 + ||\mathbf{s}_{i,2}||^2_2 \leq \beta^2 | | s i , 1 | | 2 2 + | | s i , 2 | | 2 2 ≤ β 2 tương đương với việc chứng minh rằng \beta^2 - ||\mathbf{s}_{i,1}||^2_2 - ||\mathbf{s}_{i,2}||^2_2 β 2 − | | s i , 1 | | 2 2 − | | s i , 2 | | 2 2 là không âm.
Định lý bốn bình phương của Lagrange phát biểu rằng mọi số nguyên không âm đều có thể được viết thành tổng của bốn bình phương. Do đó, chúng ta có thể tìm thấy bốn số nguyên \epsilon_{i,0}, \epsilon_{i,1}, \epsilon_{i,2}, \epsilon_{i,3} \in \mathbb{Z} ϵ i , 0 , ϵ i , 1 , ϵ i , 2 , ϵ i , 3 ∈ Z sao cho:
Các giá trị \epsilon_{i,j} ϵ i , j của chữ ký thứ i i được thêm vào bằng chứng như các hệ số của đa thức
Lưu ý rằng khi có đa thức \mathbf{a} = a_0 + a_1 X + ... + a_{d-1} X^{d-1}, a = a 0 + a 1 X + . . . + a d − 1 X d − 1 , ta có thể tính chuẩn của nó như sau (sử dụng thực tế là ||\mathbf{a}||^2 = ct(\langle \mathbf{a}, \sigma_{-1}(\mathbf{a}) \rangle) | | a | | 2 = c t ( ⟨ a , σ − 1 ( a ) ⟩ ) đối với phép tự đẳng cấu liên hợp \sigma_{-1} σ − 1 và X^d = -1 X d = − 1 ):
Chúng ta biểu thị \mathbf{a}' = a_0 - a_{d-1} X - ... - a_1 X^{d-1}. a ′ = a 0 − a d − 1 X − . . . − a 1 X d − 1 .
Bây giờ chúng ta có thể viết lại ràng buộc chuẩn thành ràng buộc LaBRADOR như sau:
Nhưng chúng ta cũng cần kiểm tra xem các phần tử chứng kiến mới đã được xây dựng chính xác chưa và các hệ số của các phần tử chứng kiến có đủ nhỏ để chúng không bao quanh q'. q ′ hay không.
Chúng ta hãy quan sát cách thể hiện ràng buộc rằng hệ số thứ j của đa thức \mathbf{a} a là một giá trị nào đó, giả sử là b: b :
Đối với mỗi \epsilon_i ϵ i, chúng ta cần chuẩn bị các ràng buộc đảm bảo \epsilon_{i,4},..., \epsilon_{i, d-1} ϵ i , 4 , . . . , ϵ i , d − 1 bằng không.
Chúng ta cũng cần đảm bảo rằng \mathbf{s}'_{i,1} s ′ i , 1 được xây dựng chính xác từ \mathbf{s}_{i,1} s i , 1 , ví dụ:
Tương tự đối với \mathbf{s}_{i,2} s i , 2 và \epsilon_i ϵ i .
Ngược lại với cách tiếp cận dựa trên tổng bốn bình phương, Dachshund sử dụng các vectơ phân tích cơ số 2, được nhân với các đa thức có hệ số boolean. Có lẽ không có sự khác biệt đáng kể về hiệu suất.
Ngăn ngừa quấn quanh
Theo cách tiếp cận trong bài báo, cần phải đảm bảo rằng hiện tượng bao quanh không xảy ra trong hai phương trình sau:
Thì ra cách đầu tiên có tính hạn chế hơn, ta thu được:
Từ phương trình thứ hai ta thu được:
Để đảm bảo điều này được thực hiện, phép chiếu Johnson–Lindenstrauss được sử dụng.
Vấn đề 2: định hình lại nhân chứng
Một hạn chế khác của giao diện Chihuahua trong bối cảnh tổng hợp chữ ký là tính kém hiệu quả khi xử lý nhiều vectơ chứng kiến, do cần phải tính toán nhiều cái gọi là đa thức rác.
Thời gian chạy của trình chứng minh—và tốc độ LaBRADOR hội tụ về trường hợp cơ sở (tức là, cần bao nhiêu bước đệ quy để nén kích thước chứng minh)—phụ thuộc vào hai tham số chính:
- đa dạng r r : số lượng vectơ chứng kiến
- hạng n n : số đa thức trong mỗi vectơ chứng kiến
Bài báo đề xuất định hình lại nhân chứng để đạt được cấu hình cân bằng hơn, nhắm mục tiêu vào các vectơ nhân chứng r = O(\sqrt{N}) r = O ( √ N ) có hạng n = N n = N , trong đó N N là số chữ ký.
Ban đầu, chứng nhân bao gồm các vectơ r = 2N r = 2 N (thậm chí còn nhiều hơn khi thêm các ràng buộc chuẩn chính xác), mỗi vectơ có hạng n = 1 n = 1. Đây là một cấu hình không cân bằng cao. Để nén đệ quy của LaBRADOR có hiệu quả, tốt nhất là r r và n n phải gần nhau hơn về độ lớn. Để giải quyết vấn đề này, lược đồ đưa ra một chiến lược đệm: chứng nhân được định hình lại sao cho n \approx N n ≈ N và r \approx \sqrt{N} r ≈ √ N , với các vectơ chứng nhân mới được đệm bằng số không khi cần.
Tuy nhiên, vấn đề này cũng được giải quyết ở giao diện Dachshund—Dachshund được thiết kế để xử lý hiệu quả số lượng lớn các đối tượng chứng kiến.
Lựa chọn nhẫn
Một khía cạnh khác là sự lựa chọn của vòng. Trong khi bài báo phân tích một số tùy chọn, cuối cùng nó áp dụng cùng một cấu hình như được sử dụng trong Lazer. Các đa thức được nhân modulo một số số nguyên tố nhỏ p_i p i (sử dụng NTT), và sau đó kết hợp các kết quả bằng cách sử dụng CRT modulo q q rõ ràng. Việc sử dụng các số nguyên tố nhỏ 16 bit p_i p i (giữa 2^{12} 2 12 và 2^{14} 2 14 ) được phân tách hoàn toàn trong \mathbb{Z}_r[X]/(X^{64} + 1) Z r [ X ] / ( X 64 + 1 ) cho phép tính số học Montgomery hiệu quả (xem thêm bài báo Greyhound ).
Bản tóm tắt
Hai phương pháp tổng hợp chữ ký—phương pháp từ bài báo Tổng hợp chữ ký Falcon với LaBRADOR và phương pháp Lazer—khá giống nhau, vì vậy chúng tôi tin rằng các chuẩn mực của mình (dựa trên mã Lazer) có liên quan đến cả hai.
Tính năng hấp dẫn nhất của chương trình tổng hợp chữ ký dựa trên mạng lưới được đánh giá chuẩn là kích thước bằng chứng của nó, trong khi trở ngại lớn nhất đối với việc áp dụng có thể là thời gian xác minh. Hiệu suất xác minh có thể được cải thiện bằng cách sử dụng các kỹ thuật đa luồng, mặc dù điều này đòi hỏi phải điều tra thêm. Tuy nhiên, các cải tiến đối với cả giao thức LaBRADOR và triển khai C của nó đã được các tác giả LaBRADOR tiến hành và những cải tiến này dự kiến sẽ tăng tốc quá trình xác minh—mặc dù hiện tại khó có thể định lượng được mức độ.
Mặc dù thời gian xác minh có thể được cải thiện nhờ các tối ưu hóa trong tương lai, nhưng có lẽ vẫn không thể so sánh với phương pháp dựa trên hàm băm (xem bảng bên dưới), trong đó quá trình xác minh chỉ mất vài mili giây.
| Hệ mét | LaBRADOR + Falcon (10000 chữ ký, 1 chủ đề) | Dựa trên băm (8192 chữ ký, 4 luồng) |
|---|---|---|
| Kích thước bản in thử | 74,07KB | 1,7 MB (mục tiêu ~128 KB với tối ưu hóa) |
| Thời gian chứng minh | 5,95 giây | 5 giây |
| Thời gian xác minh | 2,65 giây | 106 giây |
| Bảo mật PQ | Có (dựa trên mạng lưới) | Có (dựa trên hàm băm: chữ ký Poseidon2, Keccak trong PCS merklization) |
| Song song hóa | Để được khám phá | Rất tốt — sử dụng 4 luồng; tỷ lệ gần như tuyến tính lên đến 4, bán tuyến tính nhưng hiệu quả vượt quá |
Tóm lại, sơ đồ LaBRADOR có vẻ rất phù hợp với những hạn chế cụ thể phát sinh trong quá trình tổng hợp chữ ký Falcon. Để cải thiện thời gian xác minh, việc khám phá các kỹ thuật ủy quyền tương tự như Dory có thể là một hướng đi đầy hứa hẹn. Các giao thức này làm giảm độ phức tạp của trình xác minh và đặc biệt hấp dẫn trong các tình huống mà bằng chứng lớn nhưng trình xác minh bị hạn chế về tài nguyên.