Xem lại DAS an toàn trong một và hai chiều

Tác giả: Benedikt ( @b-wagn ), Francesco ( @fradamt )

Tất cả mã đều có trong sổ tay .

I. Giới thiệu

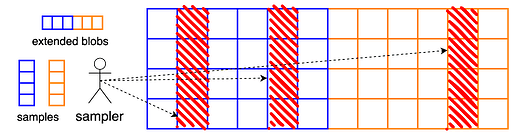
Với bản nâng cấp Fusaka , Ethereum sẽ giới thiệu cơ chế lấy mẫu khả dụng dữ liệu (DAS) có tên là PeerDAS . Các đơn vị dữ liệu cơ bản, blob , được mở rộng theo chiều ngang bằng mã Reed-Solomon và được sắp xếp thành các hàng của một ma trận. Các mẫu sau đó được chia thành các cột.

hình ảnh 2752×736 133 KB

Các cột cũng là đơn vị truyền tải trên mạng, và hiện tại không thể trao đổi bất kỳ cột nào nhỏ hơn một cột. Do đó, phiên bản PeerDAS đầu tiên này còn thiếu hai tính năng:

• Tái cấu trúc một phần : có thể đóng góp vào quá trình tái cấu trúc bằng cách chỉ tái cấu trúc và gieo lại một phần dữ liệu, ví dụ, chỉ một hàng (hoặc một vài hàng) thay vì toàn bộ ma trận.
• Khả năng tương thích hoàn toàn với mempool : các giao dịch đi kèm với các blob/hàng và thường được phân phối trước trong mempool. Tuy nhiên, bất kỳ blob nào bị thiếu sẽ ngăn một nút xây dựng các cột, khiến tất cả các blob mempool khác trở nên vô dụng.

Để giải quyết những hạn chế này, nhắn tin cấp độ tế bào đã được xem xét mạnh mẽ như một ứng cử viên cho phiên bản tiếp theo của giao thức (xem ví dụ tại đây ). Vì đây cũng là một thành phần quan trọng của cấu trúc DAS hai chiều , điều này đặt ra câu hỏi liệu chúng ta có nên:

• Nâng cao PeerDAS 1D với nhắn tin cấp độ tế bào hoặc
• Chuyển sang cấu trúc 2D.

Hoặc ít nhất là liệu quá trình chuyển đổi này có phải là một lần lặp lại tiếp theo hay không. Trong bài viết này, chúng tôi so sánh hiệu quả của hai phương pháp này với giả định rằng cả hai đều hướng đến mục tiêu cung cấp cùng một mức độ bảo mật trong khi giảm thiểu mức tiêu thụ băng thông .

Tuyên bố miễn trừ trách nhiệm: Chúng tôi sẽ hoàn toàn bỏ qua tính bảo mật của "lớp mật mã", tức là các thuộc tính bảo mật của các cam kết KZG được sử dụng. Lớp này đã được nghiên cứu rộng rãi tại đây và tại đây . Trọng tâm của chúng tôi là các thuộc tính bảo mật thống kê liên quan đến quy trình lấy mẫu, coi lớp mật mã là lý tưởng.

Bối cảnh: Lấy mẫu tính khả dụng của dữ liệu

Chúng ta hãy bắt đầu bằng cách tóm tắt lại ý tưởng cốt lõi đằng sau việc lấy mẫu dữ liệu khả dụng (DAS).

Trong DAS, người đề xuất nắm giữ một phần dữ liệu và muốn phân phối nó trên mạng. Các máy khách (có thể là các nút đầy đủ hoặc trình xác thực) muốn xác minh rằng dữ liệu này thực sự khả dụng mà không cần phải tải xuống toàn bộ.

Để đạt được điều này, bên đề xuất mở rộng dữ liệu bằng mã xóa . Sau đó, mỗi máy khách sẽ cố gắng tải xuống k k ký hiệu ngẫu nhiên của từ mã kết quả và đối chiếu chúng với một cam kết mật mã ngắn gọn mà tất cả các máy khách đều tải xuống. Trong ngữ cảnh DAS, các ký hiệu này còn được gọi là mẫu hoặc truy vấn . Máy khách chỉ chấp nhận dữ liệu (ví dụ: bao gồm khối tương ứng trong lựa chọn phân nhánh của họ) nếu tất cả k k truy vấn được xác minh thành công.

Trực giác cấp cao đằng sau tính bảo mật của DAS (chống lại người đề xuất có khả năng gây hại) là:

• Cam kết mật mã đảm bảo rằng người đề xuất đang cam kết với một từ mã hợp lệ (xem khái niệm ràng buộc mã tại đây );
• Nếu đủ số lượng khách hàng chấp nhận, các truy vấn tập thể của họ sẽ cho phép tái tạo lại toàn bộ dữ liệu, nhờ vào các thuộc tính của mã xóa.

Bài viết này tập trung vào điểm thứ hai: Quá trình tái cấu trúc thực sự được thực hiện như thế nào? Bao nhiêu máy khách là đủ ? Và chúng ta nên thiết lập tham số k k như thế nào?

Chúng ta bắt đầu bằng cách giải quyết câu hỏi đầu tiên, giải thích ý nghĩa của việc tái cấu trúc một phần . Sau đó, chúng ta chuyển trọng tâm sang vấn đề bảo mật.

Bối cảnh: Tái thiết một phần

Một trong những câu hỏi trọng tâm trong DAS là: ai có thể tái tạo dữ liệu, và khi nào ? Giả sử chúng ta có một "siêu nút" toàn năng có thể tải xuống đủ mẫu từ mạng để tái tạo toàn bộ dữ liệu được mã hóa thông qua mã xóa. Trong trường hợp đó, nếu chỉ thiếu một vài ký hiệu mã - có thể bị giữ lại bởi một người đề xuất có ác ý - thì siêu nút này có thể dễ dàng tính toán lại các phần bị thiếu và đưa chúng trở lại mạng (hay còn gọi là gieo hạt lại ). Cuối cùng, các ký hiệu này sẽ lan truyền và tất cả máy khách đều chấp nhận.

Thiết lập này làm dấy lên mối lo ngại về việc phụ thuộc vào các siêu nút mạnh như vậy, điều này có thể là một yếu tố tập trung hóa. Trên thực tế, ngay cả khi chúng ta sử dụng mã xóa với ngưỡng tái tạo tối thiểu, tức mã MDS như Reed-Solomon , siêu nút vẫn cần tải xuống số lượng mẫu bằng với toàn bộ dữ liệu gốc trước khi có thể tái tạo.

Đây chính là lúc khái niệm tái cấu trúc một phần xuất hiện. Chúng ta nói rằng một mã cho phép tái cấu trúc một phần nếu các phần dữ liệu cục bộ, nhỏ có thể được phục hồi bằng cách sử dụng ít mẫu hơn đáng kể so với số lượng mẫu cần thiết cho tái cấu trúc toàn bộ. Thay vì cần một siêu nút để thu thập gần như tất cả các phần, nhiều nút nhỏ hơn có thể tái cấu trúc độc lập các phần dữ liệu. Theo cách này, tái cấu trúc một phần cho phép phân bổ tác vụ tái cấu trúc cho nhiều bên tham gia, giảm sự phụ thuộc vào các siêu nút tập trung.

Bên cạnh việc tăng cường tính mạnh mẽ của mạng bằng cách giảm sự phụ thuộc vào các nút mạnh hơn, việc phân bổ tải CPU cho việc tái tạo và tải băng thông cho việc gieo lại dữ liệu đã tái tạo cũng có thể được coi là một cải tiến về hiệu suất. Hiện tại, việc tái tạo khó có thể giúp dữ liệu lan truyền theo đường dẫn quan trọng, điều mà người ta có thể mong đợi là một lợi ích khác của việc sử dụng mã hóa xóa, vì mất khoảng 100ms để tái tạo một blob duy nhất , với tất cả các bằng chứng . Bằng cách phân bổ tải này trên nhiều nút, mỗi nút chỉ chịu trách nhiệm cho một hoặc một vài blob, mã hóa xóa có thể hữu ích cho nhiều mục đích hơn là chỉ đảm bảo an ninh.

Bối cảnh: Độ vững chắc của tập hợp con

Trong bài viết này, chúng tôi muốn so sánh các lược đồ mã hóa khác nhau (1D và 2D) về hiệu quả của chúng, với giả định rằng tất cả chúng đều đạt được cùng mức độ bảo mật . Để so sánh này có ý nghĩa, trước tiên chúng ta cần hiểu rõ "bảo mật" bao hàm điều gì trong bối cảnh DAS.

Khái niệm bảo mật mà chúng tôi xem xét được gọi là độ vững chắc của tập con và xem xét một đối thủ thích ứng. Khái niệm này được giới thiệu chính thức dưới dạng Định nghĩa 2 trong Tài liệu Nền tảng của DAS , và nó cũng củng cố cơ sở bảo mật của PeerDAS .

Theo trực giác, độ chính xác của tập con mô hình hóa một đối thủ mạnh mẽ, người quan sát các truy vấn được thực hiện bởi một tập hợp lớn gồm n n máy khách/nút. Sau đó, đối thủ có thể tự động quyết định biểu tượng nào sẽ hiển thị và biểu tượng nào sẽ ẩn, từ đó tạo ra góc nhìn mà mỗi nút nhìn thấy. Đối thủ cũng chọn một phần các nút — ví dụ, \epsilon n \leq n ϵ n ≤ n với một số \epsilon > 0 ϵ > 0 cố định — và cố gắng đánh lừa chúng tin rằng dữ liệu đã có sẵn đầy đủ. Đáng chú ý, lựa chọn này có thể phụ thuộc vào các truy vấn mà các nút đã thực hiện. Sau đó, chúng ta xem xét xác suất p p mà đối thủ thắng trò chơi này, tức là

• tất cả các nút \epsilon n ϵ n đều chấp nhận và
• dữ liệu không có sẵn đầy đủ; nghĩa là: người ta không thể tái tạo dữ liệu từ các truy vấn của họ.

Với mục đích của chúng tôi, chúng tôi muốn p p không vượt quá 2^{-30} 2 − 30 (cho bất kỳ đối thủ nào). Dưới đây, chúng tôi sẽ thiết lập số lượng truy vấn k k trên mỗi nút tùy thuộc vào n n , \epsilon ϵ và lược đồ mã hóa, sao cho p \leq 2^{-30} p ≤ 2 − 30 được đảm bảo.

Tác động và Lựa chọn của \epsilon ϵ :
Khái niệm bảo mật được mô tả ở trên được tham số hóa bởi \epsilon \in (0, 1] ϵ ∈ ( 0 , 1 ] , mô hình hóa phần các nút mà kẻ tấn công cố gắng đánh lừa . Từ định nghĩa chính thức và phép rút gọn mật mã đơn giản, ta có thể suy ra rằng độ tin cậy của tập con đối với một \epsilon ϵ nhất định (với n n ) cố định hàm ý độ tin cậy của tập con đối với bất kỳ \epsilon' \geq \epsilon ϵ ′ ≥ ϵ lớn hơn nào . Nói cách khác: nếu kẻ tấn công không thể đánh lừa một phần các nút \epsilon ϵ , thì chắc chắn nó không thể đánh lừa một phần lớn hơn \epsilon' ϵ ′ .

Nhưng điều này liên quan như thế nào đến giao thức đồng thuận tổng thể? Giả sử chúng ta biết rằng kẻ tấn công không thể lừa được nhiều hơn một phần nhỏ \epsilon ϵ các nút. Mỗi nút bị lừa thực chất hoạt động như một nút độc hại bổ sung trong quá trình đồng thuận. Do đó, khi sử dụng phương pháp lấy mẫu tính khả dụng của dữ liệu, kẻ tấn công sẽ có thêm tối đa một phần nhỏ \epsilon ϵ các nút độc hại rõ ràng.

Ví dụ, nếu sự đồng thuận không có DAS cho phép tối đa <{1}/{3} < 1 / 3 nút độc hại, thì với DAS, hệ thống hiện chỉ có thể cho phép tối đa <{1}/{3} - \epsilon < 1 / 3 − ϵ nút độc hại.

Do đó, trên thực tế, chúng ta phải chọn \epsilon ϵ nhỏ, chẳng hạn, \epsilon = 1\% ϵ = 1 % , để đảm bảo ảnh hưởng của đối thủ vẫn không đáng kể.

II. PeerDAS - Xây dựng 1D

Trong phần này, chúng tôi sẽ giải thích cách thức hoạt động của PeerDAS, tính năng này sẽ được tích hợp trong bản nâng cấp Fusaka. Chúng tôi cũng giải thích cách thức nhắn tin ở cấp độ tế bào cho phép tái tạo một phần.

Nó hoạt động như thế nào

Chúng tôi mô tả cách mã hóa dữ liệu và cách khách hàng thực hiện truy vấn, bỏ qua mọi thứ liên quan đến "lớp mật mã", ví dụ như cam kết và mở.

Một blob là một tập hợp m m ô, trong đó mỗi ô chứa f f phần tử trường. Trong cài đặt tham số hiện tại của PeerDAS, chúng ta có f = 64 f = 64 phần tử trường trên mỗi ô, và m = 64 m = 64 ô trên mỗi blob. Để xem xét các kích thước ô khác nhau, chúng ta đặt fm = 4096 f m = 4096 là hằng số (tức là cố định kích thước dữ liệu) và thay đổi f \in \{64,32,16,8\} f ∈ { 64 , 32 , 16 , 8 } , đặt m = 4096 / f m = 4096 / f .

Để mã hóa một blob đơn lẻ, ta mở rộng blob bằng mã Reed-Solomon với tốc độ 1/2 1/2 , tạo ra 2m 2 m ô, hay tương đương, 2fm = 8192 2 f m = 8192 phần tử trường. Trong PeerDAS, chúng tôi áp dụng quy trình mã hóa này cho b b b một cách độc lập và xem các blob mở rộng dưới dạng các hàng trong ma trận ô a b \times 2m b × 2 m .

Bây giờ, máy khách truy vấn toàn bộ các cột của ma trận này, tức là họ cố gắng tải xuống b b cell cùng một lúc. Điều này có nghĩa là các "ký hiệu" hoặc mã xóa của chúng tôi là các cột của ma trận blob mở rộng. Từ bất kỳ m m nào trong số các cột này, người ta có thể tái tạo toàn bộ ma trận và do đó là dữ liệu.

Cơ sở hạ tầng mạng cụ thể hỗ trợ chức năng lấy mẫu là các chủ đề GossipSub cho các cột , tức là các mạng con mà chỉ các nút quan tâm đến một mẫu cụ thể (= cột) mới tham gia.

Tái thiết một phần

Như dự đoán, thiết kế PeerDAS hiện tại không hỗ trợ tái tạo một phần. Tuy nhiên, ngay cả mã hóa một chiều như vậy về nguyên tắc cũng có thể hỗ trợ tính năng này, khi được áp dụng độc lập cho nhiều blob , như trong PeerDAS. Trên thực tế, bằng cách sử dụng các đơn vị dọc nhỏ hơn cột, chẳng hạn như ô, chắc chắn có thể tái tạo chỉ một phần của toàn bộ ma trận, ví dụ như các hàng hoặc nhóm hàng riêng lẻ. Điều này đặt ra hai thách thức:

1. Gieo lại một phần : khi một nút tái tạo một hàng duy nhất, nó không tái tạo bất kỳ mẫu (cột) đầy đủ nào, nhưng nó vẫn cần có khả năng đóng góp dữ liệu được tái tạo trở lại mạng.
2. Thu thập đủ số lượng tế bào để tái tạo : khi chỉ lấy mẫu các cột, khả năng tái tạo là tất cả hoặc không có gì, nghĩa là một nút hoặc thu thập đủ số lượng cột để tái tạo toàn bộ ma trận, hoặc không thể tái tạo bất kỳ phần nào của ma trận. Nói cách khác, chỉ các siêu nút mới có thể tham gia vào quá trình tái tạo. Chúng tôi muốn các nút có thể làm như vậy trong khi vẫn chỉ tải xuống một phần nhỏ của toàn bộ dữ liệu.

Có nhiều cách tiếp cận chúng một cách nổi tiếng, cùng nhau chúng ta có thể tái tạo lại một phần:

1. Nhắn tin ở cấp độ ô : cho phép các nút trao đổi ô thay vì toàn bộ cột, do đó, một nút tái tạo một hàng có thể gieo lại hàng đó theo từng ô , ít nhất là trong các chủ đề cột mà chúng tham gia.
2. Chủ đề hàng : các nút cũng cố gắng tải xuống một số hàng bằng cách tham gia vào các chủ đề hàng, cũng được trang bị nhắn tin cấp độ ô. Quan trọng là, đây không phải là lấy mẫu và không có ý nghĩa bảo mật nào đối với số lượng hàng được lấy , vì vậy ngay cả việc tham gia vào một chủ đề hàng duy nhất cũng đủ. Trên thực tế, việc lấy mẫu các hàng là vô nghĩa trong cấu trúc 1D, vì không có sự dư thừa theo chiều dọc. Mục đích của một chủ đề hàng chỉ là các ô từ các chủ đề cột có thể chảy vào nó và cho phép tái tạo từng hàng, mà không cần bất kỳ siêu nút nào . Các ô được tái tạo sau đó có thể chảy từ chủ đề hàng vào tất cả các chủ đề cột, một lần nữa mà không cần bất kỳ nút đơn lẻ nào tham gia vào tất cả chúng.

Lưu ý: việc thiếu dự phòng theo chiều dọc có nghĩa là chúng ta cần mọi chủ đề hàng đều thực hiện thành công nhiệm vụ tái cấu trúc của nó. Nếu ngay cả một chủ đề hàng đơn lẻ cũng không thực hiện được (ví dụ do tấn công cấp độ mạng chỉ giới hạn ở chủ đề đó), toàn bộ quá trình tái cấu trúc sẽ không thể hoàn tất.

Số lượng mẫu

Bây giờ, hãy xác định số lượng mẫu k k trên mỗi máy khách cho PeerDAS. Như đã thảo luận ở trên, chúng ta muốn chọn k k sao cho xác suất p p mà kẻ tấn công phá vỡ tính toàn vẹn của tập hợp con không vượt quá 2^{-30} 2 − 30 .

Tính bảo mật của PeerDAS đã được phân tích sâu rộng tại đây và tại đây . Công trình sau được xây dựng dựa trên khuôn khổ bảo mật từ đây , và một giới hạn cụ thể cho tính toàn vẹn của tập con có thể được suy ra bằng cách kết hợp Bổ đề 1 và Bổ đề 3 tại đây . Cuối cùng, tất cả những điều này tạo ra cùng một giới hạn cho tính toàn vẹn của tập con, cụ thể là:

p \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot (\frac{m-1}{2m})^{kn\epsilon} \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot 2^{-kn\epsilon}. p ≤ ( n n ϵ ) ⋅ ( 2 m m − 1 ) ⋅ ( m − 1 2 m ) k n ϵ ≤ ( n n ϵ ) ⋅ ( 2 m m − 1 ) ⋅ 2 − k n ϵ .

Theo trực giác, nhị thức đầu tiên tính đến khả năng của đối thủ trong việc tự do và thích ứng chọn n\epsilon n ϵ nút để đánh lừa, nhị thức thứ hai tính đến việc đối thủ chọn m-1 m − 1 ký hiệu để cung cấp cho các nút này và số hạng cuối cùng là xác suất tất cả các mẫu của chúng sẽ nằm trong phần mã hóa có sẵn này.

Nếu chúng ta muốn p \leq 2^{-30} p ≤ 2 − 30 và n,m,\epsilon n , m , ϵ được đưa ra, chúng ta cần đặt

k \geq \frac{1}{n\epsilon} \left( \log_2 \binom{n}{n\epsilon} + \log_2 \binom{2m}{m-1} + 30 \right) k ≥ 1 n ϵ ( log 2 ( n n ϵ ) + logarit 2 ( 2 m m − 1 ) + 30 ) .

Sau đây là mã để tính k k :

 from math import comb, log2, ceil # used later from tabulate import tabulate # used later import numpy as np # used later import matplotlib.pyplot as plt # used later def min_samples_per_node ( n: int , m: int , r: int = 2 , eps: float = 0.01 ): """Finds the smallest integer k such that k samples per nodeachieve security of 30 bits for the 1D construction.Inputs:n: total number of nodesm: number of symbols in original datar: inverse coding rate (total symbols = r*m), default=2eps: fraction of nodes to be fooled (0 < eps <= 1), default=0.01Returns:Smallest integer k satisfying the bound""" neps = int (n * eps)binom_n = comb(n, neps)binom_m = comb(m*r, m- 1 )log2_binom = log2(binom_n) + log2(binom_m)k = -(log2_binom + 30 )/(n*eps*log2( 1 /r)) return ceil(k)

Các cột cũng là đơn vị truyền tải trên mạng, và hiện tại không thể trao đổi bất kỳ cột nào nhỏ hơn một cột. Do đó, phiên bản PeerDAS đầu tiên này còn thiếu hai tính năng:

• Tái cấu trúc một phần : có thể đóng góp vào quá trình tái cấu trúc bằng cách chỉ tái cấu trúc và gieo lại một phần dữ liệu, ví dụ, chỉ một hàng (hoặc một vài hàng) thay vì toàn bộ ma trận.
• Khả năng tương thích hoàn toàn với mempool : các giao dịch đi kèm với các blob/hàng và thường được phân phối trước trong mempool. Tuy nhiên, bất kỳ blob nào bị thiếu sẽ ngăn một nút xây dựng các cột, khiến tất cả các blob mempool khác trở nên vô dụng.

Để giải quyết những hạn chế này, nhắn tin cấp độ tế bào đã được xem xét mạnh mẽ như một ứng cử viên cho phiên bản tiếp theo của giao thức (xem ví dụ tại đây ). Vì đây cũng là một thành phần quan trọng của cấu trúc DAS hai chiều , điều này đặt ra câu hỏi liệu chúng ta có nên:

• Nâng cao PeerDAS 1D với nhắn tin cấp độ tế bào hoặc
• Chuyển sang cấu trúc 2D.

Hoặc ít nhất là liệu quá trình chuyển đổi này có phải là một lần lặp lại tiếp theo hay không. Trong bài viết này, chúng tôi so sánh hiệu quả của hai phương pháp này với giả định rằng cả hai đều hướng đến mục tiêu cung cấp cùng một mức độ bảo mật trong khi giảm thiểu mức tiêu thụ băng thông .

Tuyên bố miễn trừ trách nhiệm: Chúng tôi sẽ hoàn toàn bỏ qua tính bảo mật của "lớp mật mã", tức là các thuộc tính bảo mật của các cam kết KZG được sử dụng. Lớp này đã được nghiên cứu rộng rãi tại đây và tại đây . Trọng tâm của chúng tôi là các thuộc tính bảo mật thống kê liên quan đến quy trình lấy mẫu, coi lớp mật mã là lý tưởng.

Bối cảnh: Lấy mẫu tính khả dụng của dữ liệu

Chúng ta hãy bắt đầu bằng cách tóm tắt lại ý tưởng cốt lõi đằng sau việc lấy mẫu dữ liệu khả dụng (DAS).

Trong DAS, người đề xuất nắm giữ một phần dữ liệu và muốn phân phối nó trên mạng. Các máy khách (có thể là các nút đầy đủ hoặc trình xác thực) muốn xác minh rằng dữ liệu này thực sự khả dụng mà không cần phải tải xuống toàn bộ.

Để đạt được điều này, bên đề xuất mở rộng dữ liệu bằng mã xóa . Sau đó, mỗi máy khách sẽ cố gắng tải xuống k k ký hiệu ngẫu nhiên của từ mã kết quả và đối chiếu chúng với một cam kết mật mã ngắn gọn mà tất cả các máy khách đều tải xuống. Trong ngữ cảnh DAS, các ký hiệu này còn được gọi là mẫu hoặc truy vấn . Máy khách chỉ chấp nhận dữ liệu (ví dụ: bao gồm khối tương ứng trong lựa chọn phân nhánh của họ) nếu tất cả k k truy vấn được xác minh thành công.

Trực giác cấp cao đằng sau tính bảo mật của DAS (chống lại người đề xuất có khả năng gây hại) là:

• Cam kết mật mã đảm bảo rằng người đề xuất đang cam kết với một từ mã hợp lệ (xem khái niệm ràng buộc mã tại đây );
• Nếu đủ số lượng khách hàng chấp nhận, các truy vấn tập thể của họ sẽ cho phép tái tạo lại toàn bộ dữ liệu, nhờ vào các thuộc tính của mã xóa.

Bài viết này tập trung vào điểm thứ hai: Quá trình tái cấu trúc thực sự được thực hiện như thế nào? Bao nhiêu máy khách là đủ ? Và chúng ta nên thiết lập tham số k k như thế nào?

Chúng ta bắt đầu bằng cách giải quyết câu hỏi đầu tiên, giải thích ý nghĩa của việc tái cấu trúc một phần . Sau đó, chúng ta chuyển trọng tâm sang vấn đề bảo mật.

Bối cảnh: Tái thiết một phần

Một trong những câu hỏi trọng tâm trong DAS là: ai có thể tái tạo dữ liệu, và khi nào ? Giả sử chúng ta có một "siêu nút" toàn năng có thể tải xuống đủ mẫu từ mạng để tái tạo toàn bộ dữ liệu được mã hóa thông qua mã xóa. Trong trường hợp đó, nếu chỉ thiếu một vài ký hiệu mã - có thể bị giữ lại bởi một người đề xuất có ác ý - thì siêu nút này có thể dễ dàng tính toán lại các phần bị thiếu và đưa chúng trở lại mạng (hay còn gọi là gieo hạt lại ). Cuối cùng, các ký hiệu này sẽ lan truyền và tất cả máy khách đều chấp nhận.

Thiết lập này làm dấy lên mối lo ngại về việc phụ thuộc vào các siêu nút mạnh như vậy, điều này có thể là một yếu tố tập trung hóa. Trên thực tế, ngay cả khi chúng ta sử dụng mã xóa với ngưỡng tái tạo tối thiểu, tức mã MDS như Reed-Solomon , siêu nút vẫn cần tải xuống số lượng mẫu bằng với toàn bộ dữ liệu gốc trước khi có thể tái tạo.

Đây chính là lúc khái niệm tái cấu trúc một phần xuất hiện. Chúng ta nói rằng một mã cho phép tái cấu trúc một phần nếu các phần dữ liệu cục bộ, nhỏ có thể được phục hồi bằng cách sử dụng ít mẫu hơn đáng kể so với số lượng mẫu cần thiết cho tái cấu trúc toàn bộ. Thay vì cần một siêu nút để thu thập gần như tất cả các phần, nhiều nút nhỏ hơn có thể tái cấu trúc độc lập các phần dữ liệu. Theo cách này, tái cấu trúc một phần cho phép phân bổ tác vụ tái cấu trúc cho nhiều bên tham gia, giảm sự phụ thuộc vào các siêu nút tập trung.

Bên cạnh việc tăng cường tính mạnh mẽ của mạng bằng cách giảm sự phụ thuộc vào các nút mạnh hơn, việc phân bổ tải CPU cho việc tái tạo và tải băng thông cho việc gieo lại dữ liệu đã tái tạo cũng có thể được coi là một cải tiến về hiệu suất. Hiện tại, việc tái tạo khó có thể giúp dữ liệu lan truyền theo đường dẫn quan trọng, điều mà người ta có thể mong đợi là một lợi ích khác của việc sử dụng mã hóa xóa, vì mất khoảng 100ms để tái tạo một blob duy nhất , với tất cả các bằng chứng . Bằng cách phân bổ tải này trên nhiều nút, mỗi nút chỉ chịu trách nhiệm cho một hoặc một vài blob, mã hóa xóa có thể hữu ích cho nhiều mục đích hơn là chỉ đảm bảo an ninh.

Bối cảnh: Độ vững chắc của tập hợp con

Trong bài viết này, chúng tôi muốn so sánh các lược đồ mã hóa khác nhau (1D và 2D) về hiệu quả của chúng, với giả định rằng tất cả chúng đều đạt được cùng mức độ bảo mật . Để so sánh này có ý nghĩa, trước tiên chúng ta cần hiểu rõ "bảo mật" bao hàm điều gì trong bối cảnh DAS.

Khái niệm bảo mật mà chúng tôi xem xét được gọi là độ vững chắc của tập con và xem xét một đối thủ thích ứng. Khái niệm này được giới thiệu chính thức dưới dạng Định nghĩa 2 trong Tài liệu Nền tảng của DAS , và nó cũng củng cố cơ sở bảo mật của PeerDAS .

Theo trực giác, độ chính xác của tập con mô hình hóa một đối thủ mạnh mẽ, người quan sát các truy vấn được thực hiện bởi một tập hợp lớn gồm n n máy khách/nút. Sau đó, đối thủ có thể tự động quyết định biểu tượng nào sẽ hiển thị và biểu tượng nào sẽ ẩn, từ đó tạo ra góc nhìn mà mỗi nút nhìn thấy. Đối thủ cũng chọn một phần các nút — ví dụ, \epsilon n \leq n ϵ n ≤ n với một số \epsilon > 0 ϵ > 0 cố định — và cố gắng đánh lừa chúng tin rằng dữ liệu đã có sẵn đầy đủ. Đáng chú ý, lựa chọn này có thể phụ thuộc vào các truy vấn mà các nút đã thực hiện. Sau đó, chúng ta xem xét xác suất p p mà đối thủ thắng trò chơi này, tức là

• tất cả các nút \epsilon n ϵ n đều chấp nhận và
• dữ liệu không có sẵn đầy đủ; nghĩa là: người ta không thể tái tạo dữ liệu từ các truy vấn của họ.

Với mục đích của chúng tôi, chúng tôi muốn p p không vượt quá 2^{-30} 2 − 30 (cho bất kỳ đối thủ nào). Dưới đây, chúng tôi sẽ thiết lập số lượng truy vấn k k trên mỗi nút tùy thuộc vào n n , \epsilon ϵ và lược đồ mã hóa, sao cho p \leq 2^{-30} p ≤ 2 − 30 được đảm bảo.

Tác động và Lựa chọn của \epsilon ϵ :
Khái niệm bảo mật được mô tả ở trên được tham số hóa bởi \epsilon \in (0, 1] ϵ ∈ ( 0 , 1 ] , mô hình hóa phần các nút mà kẻ tấn công cố gắng đánh lừa . Từ định nghĩa chính thức và phép rút gọn mật mã đơn giản, ta có thể suy ra rằng độ tin cậy của tập con đối với một \epsilon ϵ nhất định (với n n ) cố định hàm ý độ tin cậy của tập con đối với bất kỳ \epsilon' \geq \epsilon ϵ ′ ≥ ϵ lớn hơn nào . Nói cách khác: nếu kẻ tấn công không thể đánh lừa một phần các nút \epsilon ϵ , thì chắc chắn nó không thể đánh lừa một phần lớn hơn \epsilon' ϵ ′ .

Nhưng điều này liên quan như thế nào đến giao thức đồng thuận tổng thể? Giả sử chúng ta biết rằng kẻ tấn công không thể lừa được nhiều hơn một phần nhỏ \epsilon ϵ các nút. Mỗi nút bị lừa thực chất hoạt động như một nút độc hại bổ sung trong quá trình đồng thuận. Do đó, khi sử dụng phương pháp lấy mẫu tính khả dụng của dữ liệu, kẻ tấn công sẽ có thêm tối đa một phần nhỏ \epsilon ϵ các nút độc hại rõ ràng.

Ví dụ, nếu sự đồng thuận không có DAS cho phép tối đa <{1}/{3} < 1 / 3 nút độc hại, thì với DAS, hệ thống hiện chỉ có thể cho phép tối đa <{1}/{3} - \epsilon < 1 / 3 − ϵ nút độc hại.

Do đó, trên thực tế, chúng ta phải chọn \epsilon ϵ nhỏ, chẳng hạn, \epsilon = 1\% ϵ = 1 % , để đảm bảo ảnh hưởng của đối thủ vẫn không đáng kể.

II. PeerDAS - Xây dựng 1D

Trong phần này, chúng tôi sẽ giải thích cách thức hoạt động của PeerDAS, tính năng này sẽ được tích hợp trong bản nâng cấp Fusaka. Chúng tôi cũng giải thích cách thức nhắn tin ở cấp độ tế bào cho phép tái tạo một phần.

Nó hoạt động như thế nào

Chúng tôi mô tả cách mã hóa dữ liệu và cách khách hàng thực hiện truy vấn, bỏ qua mọi thứ liên quan đến "lớp mật mã", ví dụ như cam kết và mở.

Một blob là một tập hợp m m ô, trong đó mỗi ô chứa f f phần tử trường. Trong cài đặt tham số hiện tại của PeerDAS, chúng ta có f = 64 f = 64 phần tử trường trên mỗi ô, và m = 64 m = 64 ô trên mỗi blob. Để xem xét các kích thước ô khác nhau, chúng ta đặt fm = 4096 f m = 4096 là hằng số (tức là cố định kích thước dữ liệu) và thay đổi f \in \{64,32,16,8\} f ∈ { 64 , 32 , 16 , 8 } , đặt m = 4096 / f m = 4096 / f .

Để mã hóa một blob đơn lẻ, ta mở rộng blob bằng mã Reed-Solomon với tốc độ 1/2 1/2 , tạo ra 2m 2 m ô, hay tương đương, 2fm = 8192 2 f m = 8192 phần tử trường. Trong PeerDAS, chúng tôi áp dụng quy trình mã hóa này cho b b b một cách độc lập và xem các blob mở rộng dưới dạng các hàng trong ma trận ô a b \times 2m b × 2 m .

Bây giờ, máy khách truy vấn toàn bộ các cột của ma trận này, tức là họ cố gắng tải xuống b b cell cùng một lúc. Điều này có nghĩa là các "ký hiệu" hoặc mã xóa của chúng tôi là các cột của ma trận blob mở rộng. Từ bất kỳ m m nào trong số các cột này, người ta có thể tái tạo toàn bộ ma trận và do đó là dữ liệu.

Cơ sở hạ tầng mạng cụ thể hỗ trợ chức năng lấy mẫu là các chủ đề GossipSub cho các cột , tức là các mạng con mà chỉ các nút quan tâm đến một mẫu cụ thể (= cột) mới tham gia.

Tái thiết một phần

Như dự đoán, thiết kế PeerDAS hiện tại không hỗ trợ tái tạo một phần. Tuy nhiên, ngay cả mã hóa một chiều như vậy về nguyên tắc cũng có thể hỗ trợ tính năng này, khi được áp dụng độc lập cho nhiều blob , như trong PeerDAS. Trên thực tế, bằng cách sử dụng các đơn vị dọc nhỏ hơn cột, chẳng hạn như ô, chắc chắn có thể tái tạo chỉ một phần của toàn bộ ma trận, ví dụ như các hàng hoặc nhóm hàng riêng lẻ. Điều này đặt ra hai thách thức:

1. Gieo lại một phần : khi một nút tái tạo một hàng duy nhất, nó không tái tạo bất kỳ mẫu (cột) đầy đủ nào, nhưng nó vẫn cần có khả năng đóng góp dữ liệu được tái tạo trở lại mạng.
2. Thu thập đủ số lượng tế bào để tái tạo : khi chỉ lấy mẫu các cột, khả năng tái tạo là tất cả hoặc không có gì, nghĩa là một nút hoặc thu thập đủ số lượng cột để tái tạo toàn bộ ma trận, hoặc không thể tái tạo bất kỳ phần nào của ma trận. Nói cách khác, chỉ các siêu nút mới có thể tham gia vào quá trình tái tạo. Chúng tôi muốn các nút có thể làm như vậy trong khi vẫn chỉ tải xuống một phần nhỏ của toàn bộ dữ liệu.

Có nhiều cách tiếp cận chúng một cách nổi tiếng, cùng nhau chúng ta có thể tái tạo lại một phần:

1. Nhắn tin ở cấp độ ô : cho phép các nút trao đổi ô thay vì toàn bộ cột, do đó, một nút tái tạo một hàng có thể gieo lại hàng đó theo từng ô , ít nhất là trong các chủ đề cột mà chúng tham gia.
2. Chủ đề hàng : các nút cũng cố gắng tải xuống một số hàng bằng cách tham gia vào các chủ đề hàng, cũng được trang bị nhắn tin cấp độ ô. Quan trọng là, đây không phải là lấy mẫu và không có ý nghĩa bảo mật nào đối với số lượng hàng được lấy , vì vậy ngay cả việc tham gia vào một chủ đề hàng duy nhất cũng đủ. Trên thực tế, việc lấy mẫu các hàng là vô nghĩa trong cấu trúc 1D, vì không có sự dư thừa theo chiều dọc. Mục đích của một chủ đề hàng chỉ là các ô từ các chủ đề cột có thể chảy vào nó và cho phép tái tạo từng hàng, mà không cần bất kỳ siêu nút nào . Các ô được tái tạo sau đó có thể chảy từ chủ đề hàng vào tất cả các chủ đề cột, một lần nữa mà không cần bất kỳ nút đơn lẻ nào tham gia vào tất cả chúng.

Lưu ý: việc thiếu dự phòng theo chiều dọc có nghĩa là chúng ta cần mọi chủ đề hàng đều thực hiện thành công nhiệm vụ tái cấu trúc của nó. Nếu ngay cả một chủ đề hàng đơn lẻ cũng không thực hiện được (ví dụ do tấn công cấp độ mạng chỉ giới hạn ở chủ đề đó), toàn bộ quá trình tái cấu trúc sẽ không thể hoàn tất.

Số lượng mẫu

Bây giờ, hãy xác định số lượng mẫu k k trên mỗi máy khách cho PeerDAS. Như đã thảo luận ở trên, chúng ta muốn chọn k k sao cho xác suất p p mà kẻ tấn công phá vỡ tính toàn vẹn của tập hợp con không vượt quá 2^{-30} 2 − 30 .

Tính bảo mật của PeerDAS đã được phân tích sâu rộng tại đây và tại đây . Công trình sau được xây dựng dựa trên khuôn khổ bảo mật từ đây , và một giới hạn cụ thể cho tính toàn vẹn của tập con có thể được suy ra bằng cách kết hợp Bổ đề 1 và Bổ đề 3 tại đây . Cuối cùng, tất cả những điều này tạo ra cùng một giới hạn cho tính toàn vẹn của tập con, cụ thể là:

p \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot (\frac{m-1}{2m})^{kn\epsilon} \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot 2^{-kn\epsilon}. p ≤ ( n n ϵ ) ⋅ ( 2 m m − 1 ) ⋅ ( m − 1 2 m ) k n ϵ ≤ ( n n ϵ ) ⋅ ( 2 m m − 1 ) ⋅ 2 − k n ϵ .

Theo trực giác, nhị thức đầu tiên tính đến khả năng của đối thủ trong việc tự do và thích ứng chọn n\epsilon n ϵ nút để đánh lừa, nhị thức thứ hai tính đến việc đối thủ chọn m-1 m − 1 ký hiệu để cung cấp cho các nút này và số hạng cuối cùng là xác suất tất cả các mẫu của chúng sẽ nằm trong phần mã hóa có sẵn này.

Nếu chúng ta muốn p \leq 2^{-30} p ≤ 2 − 30 và n,m,\epsilon n , m , ϵ được đưa ra, chúng ta cần đặt

k \geq \frac{1}{n\epsilon} \left( \log_2 \binom{n}{n\epsilon} + \log_2 \binom{2m}{m-1} + 30 \right) k ≥ 1 n ϵ ( log 2