WHIR cho Ethereum

Tác giả: Thomas Coratger , Giacomo Fenzi

Cảm ơn Justin Drake và Tom Wambsgans vì những phản hồi sâu sắc và mang tính xây dựng.

Giới thiệu: tại sao và làm thế nào WHIR có thể được sử dụng cho Ethereum trong tương lai?

Khi Ethereum tiếp tục mở rộng quy mô, các yêu cầu đối với hệ thống chứng minh SNARK ngày càng trở nên khắt khe hơn: chứng minh phải nhỏ gọn, xác minh phải nhanh như chớp, và toàn bộ hệ thống phải đủ đơn giản và mạnh mẽ để có thể xác minh trên phần cứng tối thiểu — lý tưởng nhất là một thiết bị hạn chế như Raspberry Pi Pico 2, như Justin Drake đã đề xuất gần đây trong cuộc gọi Ethproofs số 2. Trong bối cảnh này, một ứng dụng nổi bật như một nền tảng thử nghiệm cho SNARK thế hệ tiếp theo: tổng hợp chữ ký cho chuỗi tinh gọn sắp tới của Ethereum. Nó đáp ứng các yêu cầu phù hợp — thông lượng cao, độ trễ nghiêm ngặt, chi phí xác minh tối thiểu, thiết lập hậu lượng tử — và sẽ đóng vai trò là một ví dụ điển hình trong suốt bài viết này.

Những nhu cầu này đang thúc đẩy một xu hướng rộng hơn trong các hệ thống chứng minh: sự chuyển đổi từ biểu diễn đa thức đơn biến sang đa tuyến tính trong các hệ thống chứng minh. Tuy nhiên, làm việc trong bối cảnh đa tuyến tính đòi hỏi các công cụ mới — đặc biệt là đối với thử nghiệm lân cận, nơi các giao thức như FRI (Fast Reed-Solomon Interactive Oracle Proof of Proximity) không còn hiệu quả nữa. Đây là lúc WHIR xuất hiện. WHIR là một giao thức thử nghiệm lân cận đệ quy dựa trên hàm băm cho các mã Reed-Solomon bị ràng buộc. Nó được thiết kế để hoạt động hiệu quả ở cả chế độ đơn biến và đa tuyến tính, khiến nó đủ linh hoạt cho một loạt các hệ thống chứng minh. Về cốt lõi, WHIR kết hợp hai ý tưởng tinh tế: cơ chế gấp đệ quy (lấy cảm hứng từ STIR) nén miền theo từng vòng và kiểm tra ràng buộc dựa trên tổng nhẹ (theo kiểu BaseFold) đảm bảo tính chính xác đại số với chi phí tối thiểu.

Kết quả là một công cụ thể hiện sự ngắn gọn — một đặc tính then chốt của Ethereum — bằng cách cung cấp các bằng chứng nhỏ (thường dưới 100 kilobyte với 128 bit bảo mật, dự đoán rằng mã Reed Solomon có sự đồng thuận tương quan lẫn nhau đến hết dung lượng), xác minh nhanh (thường dưới một mili giây đến vài mili giây, tùy thuộc vào hàm băm được chọn) và sử dụng bộ nhớ thấp, tất cả trong khi chỉ dựa trên các giả định mật mã dựa trên hàm băm. WHIR hỗ trợ SNARK nhỏ gọn, ít gas, cho phép tổng hợp chữ ký hiệu quả và mở đường cho các bằng chứng đệ quy trong các hệ thống mà tính đơn giản của trình xác minh là tối quan trọng.

Trong phần còn lại của bài viết này, chúng tôi sẽ giải thích cách thức hoạt động của WHIR, lý do tại sao nó quan trọng và cách nó có thể giúp định hình tương lai của các hệ thống chứng minh hiệu quả trên Ethereum.

Một số bối cảnh về SNARK hiện đại

Các SNARK hiện đại thường được xây dựng bằng cách xếp lớp một Sơ đồ Cam kết Đa thức (PCS) lên trên một Chứng minh Oracle Tương tác Đa thức (PIOP). Một ví dụ phổ biến là mô hình AIR (Biểu diễn Trung gian Đại số), trong đó người chứng minh cam kết thực hiện một dấu vết bằng cách mã hóa mỗi cột của bảng thành một đa thức đơn biến. Chiến lược này, tuy đơn giản, nhưng lại gây ra các nút thắt về khả năng mở rộng: mỗi cột trở thành một đa thức riêng biệt, dẫn đến kích thước chứng minh lớn và chi phí xác minh tốn kém — thường lên đến hàng megabyte khi liên quan đến hàng trăm cột .

Để khắc phục điều này, các hệ thống chứng minh gần đây đang chuyển từ biểu diễn đơn biến sang đa tuyến tính. Thay vì cam kết với từng cột riêng biệt, toàn bộ chứng cứ được mã hóa thành một đa thức đa tuyến tính duy nhất. Thay đổi này mang lại một số lợi thế: nén tốt hơn, biểu thức ràng buộc đơn giản hơn và kích thước chứng minh phụ thuộc vào tổng diện tích của dấu vết, thay vì hình dạng của nó. Các hệ thống như Binius , Jolt và SP1 Hypercube đã áp dụng xu hướng này — với SP1 là hệ thống đầu tiên chứng minh tính năng chứng minh theo thời gian thực cho các khối Ethereum, sử dụng các cam kết đa tuyến tính.

Kiểm chứng ràng buộc trong thiết lập đa tuyến tính này có thể được thực hiện bằng giao thức sumcheck, thay vì xây dựng và đánh giá đa thức thương. Sumcheck cung cấp tính mô-đun tốt hơn và hoạt động liền mạch với các mã hóa đa tuyến tính, mặc dù nó đi kèm với sự đánh đổi hiệu suất khi sử dụng các trường nhỏ. Hạn chế này gần đây đã được giải quyết bằng phương pháp tối ưu hóa "bỏ qua đơn biến" , phương pháp này tăng tốc sumcheck bằng cách gộp nhiều biến trong vòng đầu tiên hoàn toàn trong trường cơ sở. Bằng cách thực hiện nhiều công việc hơn ngay từ đầu trong một miền trường cơ sở rẻ tiền, bỏ qua đơn biến làm giảm các đánh giá trường mở rộng tốn kém trong các vòng sau, dẫn đến việc tăng tốc đáng kể cho trình chứng minh mà không ảnh hưởng đến tính hợp lý. Ngoài phương pháp này, các phương pháp tiếp cận khác để tăng tốc giao thức sumcheck đang được khám phá. Một hướng nghiên cứu đáng chú ý gần đây là hướng do S. Bagad và các đồng tác giả đề xuất.

Trong ngăn xếp mới này, WHIR đóng vai trò quan trọng: nó thực hiện bước kiểm tra độ gần, xác minh rằng hàm đa tuyến tính đã cam kết thực sự gần với một từ mã hợp lệ.

WHIR hoạt động như thế nào?

Phần này cung cấp lời giải thích trực quan nhưng chặt chẽ về cách thức hoạt động của WHIR, làm nổi bật các cơ chế cốt lõi mà không đi sâu vào các bằng chứng hình thức đầy đủ. Mục tiêu là cung cấp một sự hiểu biết rõ ràng và dễ hiểu cho các kỹ sư.

Kiểm tra độ gần của mã Reed-Solomon

Ở cấp độ cao, WHIR là một công cụ để xác minh rằng hàm f : \mathcal{L} \to \mathbb{F} f : L → F “gần” với một đa thức bậc thấp — và rằng đa thức này thỏa mãn một số ràng buộc đại số.

Mã Reed–Solomon là gì?

Mã Reed–Solomon là tập hợp các hàm phát sinh từ việc đánh giá các đa thức bậc thấp trên một trường hữu hạn. Chính xác hơn, giả sử ta chọn một trường hữu hạn \mathbb{F} F và một tập con \mathcal{L} \subseteq \mathbb{F} L ⊆ F được gọi là miền đánh giá. Mã Reed–Solomon bậc d d là:

Nói cách khác, đây chỉ là tất cả các bảng đánh giá khả dĩ của các đa thức bậc nhỏ hơn d d trên miền \mathcal{L} L. Khi chúng ta nói một hàm f f "nằm trong mã", ý chúng ta là nó nhất quán với đa thức đó. Khi f f "gần" với mã, ý chúng ta là nó nhất quán với một từ mã nào đó tại hầu hết các điểm trong \mathcal{L} L — điều này được gọi là độ gần.

Tại sao chúng ta quan tâm đến thử nghiệm tiệm cận?

Trong các hệ thống chứng minh, người chứng minh có thể gửi cho người kiểm chứng một hàm f f trông giống như đang đánh giá một đa thức bậc thấp — nhưng thực tế có thể không phải vậy. Để đảm bảo tính chính xác, người kiểm chứng phải kiểm tra xem f f có gần với một từ mã thực trong mã Reed–Solomon hay không. Đây chính là cốt lõi của phép kiểm tra độ gần.

Chế độ xem đa tuyến tính và mã mượt mà

WHIR hoạt động với một phiên bản mã RS có cấu trúc chặt chẽ hơn. Thay vì các đa thức tùy ý, nó sử dụng các đa thức đa tuyến tính — tức là các đa thức mà mỗi biến xuất hiện với bậc không quá 1. Ví dụ, trong các biến x, y, z x , y , z , một đa thức đa tuyến tính có thể trông giống như 3 + 2x + 5y + 7xz 3 + 2 x + 5 y + 7 x z , nhưng không phải x^2 x 2 hoặc y^2z y 2 z .

Để thực hiện điều này, WHIR giả định rằng:

• Miền \mathcal{L} L là một nhóm con nhân của \mathbb{F}^* F ∗ có kích thước là lũy thừa của 2,
• Bậc giới hạn d d cũng là lũy thừa của 2, giả sử d = 2^m d = 2 m .

Trong những điều kiện này, bất kỳ đa thức đơn biến \hat{f} ^ f nào có bậc nhỏ hơn 2^m 2 m đều có thể được coi duy nhất là một đa thức đa tuyến tính trong m m biến. Việc đánh giá đa thức ban đầu tại điểm x \in \mathcal{L} x ∈ L trở nên tương đương với việc đánh giá phần đa tuyến tính mới của nó, mà chúng ta cũng gọi là \hat{f} ^ f , tại một vectơ đặc biệt suy ra từ x x . Điều này cho chúng ta một cách diễn giải lại tinh tế sau:

Phép biến đổi này ánh xạ mỗi điểm trong miền đơn biến \mathcal{L} L thành một điểm trên siêu khối boolean m m chiều. Nó cho phép chúng ta áp dụng các kỹ thuật đa tuyến tính hiệu quả (như giao thức sumcheck) trong khi vẫn giữ được tính đơn giản của cấu trúc mã gốc.

Thêm ràng buộc vào mã

Trong nhiều giao thức, chúng ta không chỉ muốn kiểm tra xem f f có gần với một đa thức hay không — chúng ta còn muốn đảm bảo rằng đa thức này thỏa mãn một điều kiện đại số nhất định. Ví dụ, chúng ta có thể muốn áp dụng điều kiện sau:

trong đó \hat{w} ^ w là đa thức ràng buộc cố định và \sigma σ là giá trị đã biết.

Để diễn đạt điều này, WHIR sử dụng một biến thể của mã RS được gọi là mã Reed-Solomon ràng buộc . Về mặt hình thức, chúng tôi định nghĩa:

trong đó f f là đánh giá của đa thức đa tuyến tính \hat{f} ^ f trên \mathcal{L} L .

Ràng buộc này đảm bảo rằng f f không chỉ xuất phát từ một đa thức — mà còn là đa thức thỏa mãn một hằng đẳng thức đại số cụ thể.

Gấp vấn đề: nén đệ quy

Để kiểm tra độ gần hiệu quả, WHIR áp dụng kỹ thuật nén đệ quy được gọi là gấp (folding ). Lấy cảm hứng từ các giao thức như FRI và STIR , kỹ thuật gấp dần dần thu nhỏ một bài toán lớn thành một bài toán nhỏ hơn, tương đương. Mỗi vòng lặp thu hẹp miền và độ phức tạp của hàm trong khi vẫn giữ nguyên các thuộc tính thiết yếu, giúp người kiểm tra dễ dàng kiểm tra cuối cùng. Sau đủ số vòng lặp, bài toán trở nên nhỏ đến mức có thể kiểm tra trực tiếp và không tốn kém.

Vòng WHIR: kết hợp fold và sumcheck

Hoạt động cốt lõi trong quy trình này là gấp, được hiểu rõ nhất thông qua cách diễn giải Reed-Solomon xen kẽ trực quan. Thay vì một công thức đệ quy phức tạp, chúng ta có thể hình dung miền \mathcal{L} L được nhóm thành các khối nhỏ. Dữ liệu của người chứng minh trong mỗi khối định nghĩa một đa thức đa tuyến tính cục bộ nhỏ. Việc gấp toàn bộ khối khi đó cũng đơn giản như việc đánh giá đa thức cục bộ này với một phép thử ngẫu nhiên \alpha α từ trình kiểm chứng.

Về mặt toán học, nếu chúng ta cho p_y(X_1, \dots, X_k) p y ( X 1 , … , X k ) là đa thức cục bộ cho khối điểm tương ứng với một điểm y y trong miền mới nhỏ hơn, thì phép toán gấp chỉ là:

Đánh giá đơn này, sử dụng vectơ thử thách ngẫu nhiên \alpha \in \mathbb{F}^k α ∈ F k , nén thông tin từ 2^k 2 k điểm trong khối gốc thành một giá trị duy nhất cho hàm mới.

WHIR cải tiến mạnh mẽ ý tưởng này. Trong một vòng duy nhất, nó sử dụng phép thử ngẫu nhiên k chiều \alpha α để loại bỏ k biến cùng lúc bằng cách áp dụng nó vào hai quy trình song song:

• Một k k -round sumcheck giảm ràng buộc đại số chính thành một ràng buộc mới, đơn giản hơn.
• Việc gấp lại (như đánh giá cục bộ) làm giảm chính hàm đó thành một hàm nhỏ hơn.

Toàn bộ vòng này chuyển đổi thể hiện lân cận ban đầu thành một thể hiện mới nhỏ hơn đáng kể, trong đó cả đa thức ràng buộc \hat{w} ^ w và mục tiêu \sigma σ đều được cập nhật:

Điều này dẫn đến một sự gia tăng hiệu quả đáng kể. Trong khi chúng ta giảm số lượng biến đi k k (thu hẹp không gian đa thức theo hệ số 2^k 2 k ), miền đánh giá chỉ giảm một nửa. Điều này cải thiện đáng kể tốc độ mã \rho = 2^m / |\mathcal{L}| ρ = 2 m / | L | . Tốc độ mới \rho' ρ ′ được cho bởi:

Thuật ngữ 2^{-k} 2 − k xuất phát từ việc giảm không gian thông điệp (ít hệ số đa thức hơn), trong khi thuật ngữ 2^1 2 1 xuất phát từ việc chỉ giảm một nửa kích thước miền. Việc giảm tốc độ mã ở mỗi vòng là lý do chính cho độ phức tạp truy vấn thấp của WHIR.

Đảm bảo độ chắc chắn của việc gấp

Quá trình gấp được thiết kế cẩn thận để đảm bảo an toàn và chắc chắn, điều này rất cần thiết cho tính bảo mật của toàn bộ hệ thống kiểm tra.

• Việc gấp giữ nguyên khoảng cách của hàm với mã. Nếu một hàm bắt đầu ở xa bất kỳ từ mã hợp lệ nào, nó vẫn giữ nguyên khoảng cách đó sau khi gấp. Lỗi không thể bị ẩn hoặc loại bỏ bằng cách trộn đại số.
• Trong bối cảnh giải mã danh sách, nhiều từ mã hợp lệ có thể nằm gần hàm của trình chứng minh. Việc gấp lại được đảm bảo (với xác suất cao) để ánh xạ toàn bộ danh sách các từ mã gần đó một cách chính xác đến bài toán mới, nhỏ hơn. Không có giải pháp giả mạo hoặc sai lệch nào được đưa vào trong quá trình đệ quy, đảm bảo trình xác minh không bị đánh lừa.

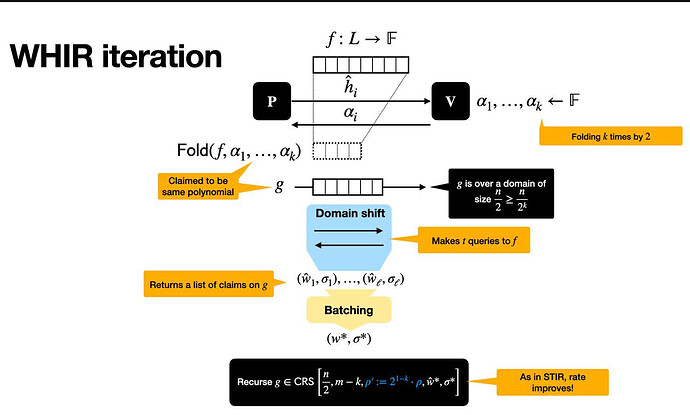
Tóm tắt về một lần lặp WHIR

Mỗi lần lặp lại WHIR, được minh họa trong hình sau, sẽ thu nhỏ vấn đề kiểm tra độ gần thành vấn đề nhỏ hơn, đồng thời vẫn giữ được tính ổn định.

hình ảnh 1280×771 91,2 KB

Quá trình này diễn ra theo ba giai đoạn chính:

Cài đặt

Chúng ta bắt đầu với một hàm f : \mathcal{L} \to \mathbb{F} f : L → F , được xác định trên một miền có cấu trúc \mathcal{L} L (một nhóm con nhân có kích thước 2^m 2 m ). Người chứng minh khẳng định rằng f f xuất phát từ việc đánh giá một đa thức đa tuyến tính \hat{f} ^ f và đa thức này thỏa mãn một ràng buộc như sau:

trong đó \hat{w} ^ w là một đa thức ràng buộc đơn giản. Đây là phát biểu cốt lõi mà chúng ta muốn kiểm chứng.

Giai đoạn tương tác

Bộ xác minh gửi một thử thách ngẫu nhiên \alpha α , hướng dẫn bộ chứng minh gấp hàm — nén hai đầu vào thành một bằng cách ẩn một biến. Điều này tạo ra một hàm mới f' = \mathrm{Fold}(f, \alpha) f ′ = F o l d ( f , α ) , được xác định trên một miền nhỏ hơn \mathcal{L}^{(2)} L ( 2 ) và bao gồm m - 1 m − 1 biến thay vì m m .

Để đảm bảo việc gấp được thực hiện một cách trung thực, người xác minh thực hiện một số kiểm tra sau:

• Nó lấy mẫu một điểm ngẫu nhiên bên ngoài miền và yêu cầu người chứng minh đánh giá, đảm bảo rằng f' f ′ thực sự xuất phát từ một đa thức bậc thấp.
• Nó lấy mẫu một vài giá trị từ hàm gấp và so sánh chúng với giá trị f f cho biết, đảm bảo tính nhất quán.
• Nó kết hợp tất cả các kiểm tra này (cùng với ràng buộc) thành một phương trình duy nhất bằng cách sử dụng tổ hợp tuyến tính ngẫu nhiên và chuẩn bị một đa thức ràng buộc mới cho vòng tiếp theo.

Yêu cầu đệ quy

Vào cuối vòng, người xác minh và người chứng minh đồng ý về một tuyên bố mới: rằng f' f ′ gần với một đa thức mới \hat{f}' ^ f ′ trên một miền nhỏ hơn và ít biến hơn, và rằng \hat{f}' ^ f ′ thỏa mãn một ràng buộc mới:

Phiên bản mới này có hình thức hoàn toàn giống với phiên bản gốc, chỉ nhỏ hơn. Sau đó, WHIR đệ quy dựa trên yêu cầu này, lặp lại các bước tương tự cho đến khi hàm đủ nhỏ để kiểm tra trực tiếp.

Điểm hay của phương pháp này là mỗi vòng có thể loại bỏ k biến cùng một lúc, đồng thời chỉ thu hẹp miền xác định theo hệ số 2 2 , và do đó giảm tốc độ. Cuối cùng, bộ kiểm chứng có độ tin cậy cao rằng hàm f ban đầu gần với một từ mã hợp lệ thỏa mãn ràng buộc — tất cả chỉ với rất ít nỗ lực.

WHIR có thể cung cấp những gì cho Ethereum

Điểm khác biệt của WHIR nằm ở cách nó thực hiện kiểm tra độ gần. Thay vì dựa vào các kỹ thuật truyền thống như FRI, WHIR sử dụng phương pháp đệ quy dựa trên phép gấp cộng với phép kiểm tra tổng , khiến nó đặc biệt hiệu quả trong môi trường đa tuyến tính (trong đó nhân chứng là một hàm trên \{0,1\}^m { 0 , 1 } m ). Thiết kế này mang lại một số lợi ích đặc biệt liên quan đến Ethereum và các môi trường onchain tương tự.

• Độ phức tạp của truy vấn cực kỳ thấp. WHIR chỉ yêu cầu một số ít truy vấn để thực hiện kiểm tra độ gần. Điều này đồng nghĩa với việc ít yêu cầu mở Merkle hơn, ít dữ liệu được gửi trên chuỗi hơn và cuối cùng là chi phí xác minh thấp hơn nhiều.

• Xác minh nhanh, thường chỉ trong vài micro giây đến vài mili giây. WHIR được thiết kế để xác minh cực nhanh — thường chỉ trong vòng vài trăm micro giây khi sử dụng các hàm băm nhanh như Keccak hoặc Blake3, và lên đến vài mili giây khi sử dụng các hàm băm tương thích SNARK như Poseidon2. WHIR đạt được điều này bằng cách kết hợp hai ý tưởng mạnh mẽ: giao thức sumcheck từ BaseFold, xác minh các danh tính đa thức với chi phí tối thiểu, và phương pháp gấp đệ quy từ STIR, giúp nén kích thước bài toán trong mỗi vòng. Kết hợp lại, chúng biến một phép kiểm tra độ gần toàn cục thành một chuỗi các phép kiểm tra nhỏ hơn, dễ xác minh.

• Bằng chứng nhỏ hơn. WHIR giảm đáng kể kích thước bằng chứng, đặc biệt là trong các thiết lập đa tuyến tính. Thay vì cam kết mỗi cột của dấu vết dưới dạng một đa thức đơn biến riêng biệt, WHIR cho phép toàn bộ bằng chứng được biểu diễn dưới dạng một đa thức đa tuyến tính duy nhất \hat{f} ^ f . Chỉ cần một cam kết, và việc gấp đệ quy giúp giảm kích thước miền theo từng vòng. Điều này dẫn đến ít cam kết hơn, ít truy vấn hơn và ít chi phí mã hóa hơn, dẫn đến các bằng chứng nhỏ hơn đáng kể ngay cả đối với các phép tính lớn.

• Mã hóa linh hoạt. WHIR hỗ trợ cả mã hóa đơn biến và đa tuyến tính. Điều này giúp nó tương thích với nhiều cấu trúc SNARK — dù chúng sử dụng mã hóa đơn biến truyền thống (như hệ thống dựa trên PLONK hoặc FRI) hay phương pháp đa tuyến tính.

Ứng dụng trên Ethereum

Nhờ các bằng chứng nhỏ gọn và xác minh ở cấp độ micro giây, WHIR đặc biệt phù hợp với các ứng dụng Ethereum:

• Rollup. Các chuyển đổi trạng thái trong rollup có thể được mã hóa dưới dạng đa thức đa tuyến tính. WHIR giúp chứng minh các chuyển đổi này một cách gọn nhẹ, với khả năng xác minh cực nhanh cho trình xác minh Ethereum L1.
• Tổng hợp chữ ký: Với nhu cầu thay thế chữ ký BLS hậu lượng tử trong tương lai, việc xác minh hiệu quả hàng nghìn chữ ký dựa trên hàm băm là tối quan trọng. WHIR cung cấp công cụ mã hóa để nén các tập hợp lớn này thành một bằng chứng duy nhất, có kích thước không đổi với dấu chân xác minh trên chuỗi tối thiểu.
• Xác minh SNARK ít tốn gas: Chi phí gas trên chuỗi chủ yếu do lưu trữ và tính toán dữ liệu. WHIR nhắm đến cả hai mục tiêu này bằng cách giảm thiểu độ phức tạp của truy vấn (giảm dữ liệu đường dẫn Merkle) và khối lượng tính toán của trình xác minh. Mặc dù một số SNARK tiền lượng tử vẫn được tối ưu hóa cao, hiệu suất của WHIR khẳng định nó là ứng cử viên hàng đầu cho các hệ thống hậu lượng tử, nơi hiệu quả trên chuỗi là không thể thương lượng, như đã được phân tích trong bài nghiên cứu này .

Tóm lại, WHIR là một giao thức tiệm cận nhanh, đệ quy và linh hoạt, phù hợp tự nhiên với các ngăn xếp SNARK hiện đại. Đối với Ethereum, nó mở ra một con đường dẫn đến các bằng chứng nhỏ hơn, rẻ hơn và nhanh hơn — đặc biệt là trong các hệ thống đã được hưởng lợi từ mã hóa đa tuyến tính.

WHIR so với FRI: Một bước nhảy vọt thế hệ trong thử nghiệm tiệm cận

FRI đã là nền tảng của các hệ thống chứng minh hiện đại, đặc biệt là STARK. Thiết kế của nó sử dụng phép gấp đệ quy để kiểm tra hiệu quả xem một hàm đã cam kết có gần với một đa thức bậc thấp hay không. Trong quy trình STARK cổ điển, trước tiên bạn kết hợp tất cả các ràng buộc đại số thành một "đa thức hợp thành" bậc cao duy nhất, sau đó chạy FRI trên đó để chứng minh rằng nó thực sự là một đa thức bậc thấp mong đợi. Cách tiếp cận này rất mạnh mẽ và đã thiết lập tính khả thi của các chứng minh hậu lượng tử với các bộ kiểm chứng đa logarit.

Tuy nhiên, bối cảnh thiết kế SNARK đang thay đổi. Các hệ thống hiện đại như Jolt, Binius và SP1 Hypercube đang dần chuyển hướng khỏi mô hình "kết hợp rồi kiểm tra" hai bước này sang một phương pháp tiếp cận đa tuyến tính tích hợp hơn. Trong mô hình mới này, các chứng minh được xây dựng xung quanh giao thức sumcheck, một công cụ để kiểm chứng các khẳng định trên các đa thức đa tuyến tính. Đây chính là nơi WHIR đại diện cho một bước tiến hóa cơ bản.

WHIR tái định nghĩa phép thử lân cận cho thế giới hiện đại, thuần túy với phép kiểm tra tổng này. Thay vì là một phép kiểm tra bậc thấp chung chung mà bạn chạy sau khi xử lý các ràng buộc, WHIR tích hợp việc xác minh ràng buộc trực tiếp vào quy trình đệ quy của nó. Một vòng FRI về cơ bản bao gồm việc gấp miền và thực hiện kiểm tra tính nhất quán trên một điểm ngẫu nhiên. Ngược lại, một vòng WHIR kết hợp phép gấp này với một phép kiểm tra tổng nhẹ, không chỉ đảm bảo phép gấp đúng mà còn chuyển các ràng buộc đại số của phép tính sang trường hợp tiếp theo, nhỏ hơn.

Sự khác biệt về kiến trúc này mang lại những lợi thế quan trọng về hiệu suất:

• Ít truy vấn hơn một cách tiệm cận. Đây là lợi thế lớn nhất của WHIR. Đối với phép tính có 2^m 2 m phần tử, độ phức tạp truy vấn của FRI tăng tuyến tính theo m m , trong khi độ phức tạp của WHIR tăng theo logarit theo m m . Đối với các phép tính quy mô lớn, đây là một cải tiến đáng kể. Trên thực tế, điều này đồng nghĩa với việc ít mở đường dẫn Merkle hơn, vốn là yếu tố chính quyết định kích thước bằng chứng và chi phí gas xác minh trên chuỗi.

• Hỗ trợ đa tuyến tính và ràng buộc gốc. WHIR là một IOP gần đúng cho các mã Reed-Solomon bị ràng buộc . Nó được xây dựng để xử lý các đa thức đa tuyến tính và các quan hệ dựa trên phép kiểm tra tổng, vốn định nghĩa các hệ thống chứng minh hiện đại. Mặc dù FRI có thể được điều chỉnh cho các cài đặt này, WHIR coi chúng như những công dân hạng nhất, mang lại một thiết kế gọn gàng và hiệu quả hơn.

• Xác minh cực kỳ nhanh chóng. Sự kết hợp giữa ít truy vấn hơn và logic xác minh nhẹ, dựa trên sumcheck cho phép WHIR đạt được thời gian xác minh chỉ trong vài trăm micro giây. Điều này làm cho nó trở nên lý tưởng cho các ứng dụng trên chuỗi, nơi mỗi micro giây hoạt động của trình xác minh đều được chuyển trực tiếp thành chi phí người dùng và thông lượng mạng.

Tổng hợp chữ ký: một trường hợp sử dụng cụ thể cho WHIR

Một trong những thách thức chính mà lớp đồng thuận tương lai của Ethereum phải đối mặt là tìm kiếm một giải pháp thay thế hậu lượng tử cho chữ ký BLS. Một số đề xuất đã được nghiên cứu — bao gồm các sơ đồ dựa trên mạng lưới và các giao thức dựa trên tích lũy — nhưng nhiều đề xuất trong số đó gặp khó khăn trong việc cân bằng giữa khả năng mở rộng, hiệu quả và bảo mật hậu lượng tử.

Một hướng đi đặc biệt hứa hẹn là sử dụng chữ ký XMSS , vốn được thiết kế dựa trên hàm băm và an toàn lượng tử. Tuy nhiên, chữ ký XMSS rất lớn và tốn kém để xác minh riêng lẻ, vì vậy việc tổng hợp trở nên cần thiết. Ý tưởng là nén hàng nghìn chữ ký riêng lẻ thành một bằng chứng duy nhất, ngắn gọn bằng cách sử dụng SNARK dựa trên hàm băm, sau đó sẽ được đăng lên chuỗi. Như đã mô tả trong bài đăng Nghiên cứu Ethereum này , một giao thức như vậy phải hỗ trợ hai hoạt động:

• Tổng hợp: nén một lượng lớn chữ ký thô thành một bằng chứng SNARK,
• Hợp nhất: kết hợp đệ quy hai bằng chứng tổng hợp hiện có thành một bằng chứng duy nhất.

Thao tác Merge đưa ra yêu cầu chứng minh đệ quy — và đây chính là điểm mạnh của WHIR. Nhờ cơ chế gấp và độ phức tạp truy vấn tối thiểu, WHIR giúp việc xây dựng các SNARK nhỏ và dễ xác minh trở nên dễ dàng hơn nhiều. Ít truy vấn hơn đồng nghĩa với việc ít phải đánh giá băm hơn, trực tiếp giảm chi phí xác minh từng lớp đệ quy. So với các cấu trúc PCS truyền thống như FRI, WHIR cho phép chứng minh đệ quy nhanh hơn nhiều — một yếu tố quan trọng cho việc tổng hợp chữ ký theo thời gian thực.

Hiệu suất ngày hôm nay và những gì tiếp theo

Một cách tự nhiên để đo lường hiệu suất trong bối cảnh này là dựa trên số lượng hàm băm (ví dụ: Poseidon2) có thể được chứng minh mỗi giây. Triển khai WHIR hiện tại của chúng tôi đạt được:

• 1 triệu hàm băm Poseidon2 mỗi giây trên GPU cao cấp (RTX 4090),
• 100.000 hàm băm Poseidon2 mỗi giây trên CPU dành cho người tiêu dùng.

Cả logic PCS ( WHI-P3 ) và lớp PIOP ( Whiraway ) đều được công khai và được tối ưu hóa tích cực. Mặc dù điểm nghẽn hiện tại là hiệu suất CPU, những nỗ lực đang được tiến hành nhằm đạt được tốc độ ngang bằng với GPU — nhắm đến mục tiêu 1 triệu băm mỗi giây trên CPU, tương đương với những gì các hệ thống như Plonky3 đã chứng minh.

Tóm tắt và các bước tiếp theo

WHIR cung cấp một phương pháp tiếp cận mới hấp dẫn cho kiểm thử tiệm cận, đặc biệt phù hợp với nhu cầu của Ethereum: kích thước bằng chứng nhỏ, xác minh nhanh chóng và tích hợp liền mạch với cả hệ thống bằng chứng đơn biến và đa tuyến tính. Chiến lược gấp đệ quy và cơ chế kiểm tra ràng buộc thông qua sumcheck khiến nó trở thành lựa chọn lý tưởng cho các ngăn xếp SNARK hiện đại, đặc biệt trong các ứng dụng đòi hỏi hiệu quả và sự đơn giản — chẳng hạn như rollup, zkVM và tổng hợp chữ ký cho chuỗi tinh gọn.

Trong bài viết này, chúng tôi tập trung vào giao thức WHIR và những ưu điểm của nó. Tuy nhiên, WHIR chỉ là một thành phần của một SNARK hoàn chỉnh. Trong bài viết tiếp theo, chúng tôi sẽ mô tả cách xây dựng một hệ thống chứng minh đầy đủ xung quanh WHIR, đồng thời chỉ ra cách nó phù hợp với một quy trình tổng hợp chữ ký hoàn chỉnh bằng mật mã dựa trên hàm băm.

Trong khi đó, chúng tôi đang tích cực tối ưu hóa việc triển khai — hướng đến tốc độ chứng minh GPU và CPU ngang bằng hoặc vượt trội hơn các hệ thống tốt nhất hiện nay, đồng thời duy trì giao thức dạng mô-đun và dễ áp dụng. Hiện tại, chúng tôi đang duy trì một triển khai WHIR mã nguồn mở dựa trên Plonky3 ( WHI-P3 ), và chúng tôi dự định sẽ đưa nó lên trực tiếp Plonky3 như một nỗ lực do cộng đồng thúc đẩy. Điều này phù hợp với tầm nhìn của chúng tôi là biến WHIR thành một sản phẩm công cộng — mở, được bảo trì tập thể và dễ dàng tích hợp vào các dự án khác.

Một số nhóm nghiên cứu zkVM đã bày tỏ sự quan tâm đến việc áp dụng WHIR và chúng tôi tin rằng sẽ có nhiều trường hợp sử dụng hơn nữa xuất hiện khi hệ sinh thái Ethereum phát triển.

Mục tiêu của chúng tôi là biến WHIR không chỉ là một ý tưởng nhanh chóng và tinh tế mà còn là nền tảng thiết thực cho thế hệ bằng chứng onchain tiếp theo.