Đây là một thứ tôi đã ấp ủ từ lâu. Chưa hoàn hảo, nhưng là đa chữ ký bảo vệ quyền riêng tư nhất có thể. Rất mong nhận được phản hồi của bạn!

Vui lòng xem qua các bài nghiên cứu khác của tôi nhưng có liên quan: Confidential Wrapped Ethereum and ZEX: Confidential Peer-to-Peer DEX .

Ngoài ra, hãy xem quaLộ trình bảo mật Ethereum tuyệt vời.

Tóm tắt

Bài báo đề xuất một phương pháp thực tế để triển khai ví đa chữ ký dựa trên Zero Knowledge (ZK) EVM nhằm bảo vệ quyền riêng tư và bảo mật cho các quyết định tập thể. Phương pháp này kết hợp ba tính năng cốt lõi: bằng chứng thành viên cây Merkle cho tính ẩn danh, mã hóa ECC ElGamal tổng hợp cho tính bảo mật phiếu bầu của người tham gia với việc ra quyết định không thiên vị, và Tạo khóa phân tán (DKG) cho tính phi tương tác trong việc suy luận và loại bỏ khóa của các thực thể tập trung, đáng tin cậy.

Giải pháp được đề xuất bao gồm hợp đồng thông minh Solidity và mạch ZK. Hợp đồng thông minh Solidity đóng vai trò là nhà máy sản xuất tài khoản và các tài khoản thực tế mà người dùng tương tác để tạo ra các hợp đồng đa chữ ký và thực hiện các đề xuất tập thể. Hợp đồng ZK chịu trách nhiệm kiểm tra xem người dùng có thuộc các tập hợp đa chữ ký hay không và xác minh quyết định của họ về việc có nên thực hiện đề xuất hay không, mà không tiết lộ kết quả trung gian.

Nhược điểm của phương pháp đề xuất là tất cả những người tham gia đa chữ ký phải bỏ phiếu cho đề xuất để tính toán kết quả.

1. Giới thiệu

Tính minh bạch của blockchain công khai mang lại vô số lợi thế, bao gồm khả năng truy xuất nguồn gốc hành động được cải thiện, khả năng xác minh thực thi và tính minh bạch của dữ liệu, sẵn sàng cho mọi người. Tuy nhiên, nó đặt ra những thách thức đặc thù trong việc ra quyết định đa phương, đặc biệt là trong việc bảo vệ quyền riêng tư và ngăn chặn sự thiên vị trong bỏ phiếu — những khía cạnh cơ bản của một ví đa chữ ký an toàn và công bằng.

Mục tiêu là tạo ra một hệ thống đa chữ ký đơn giản, không cần cấp phép, không tiết lộ bất cứ thông tin gì về thành viên và đảm bảo với những người bỏ phiếu đa chữ ký rằng lá phiếu của họ được giữ bí mật và lựa chọn của họ không bị ảnh hưởng bởi số phiếu của những người tham gia bỏ phiếu sớm.

Đa chữ ký sẽ cho phép người dùng được đưa vào/loại trừ khỏi danh sách thành viên, cấu hình "ngưỡng chữ ký" và thực hiện các giao dịch được phê duyệt tập thể, với (gần như) không có bất kỳ sự xâm phạm nào đến quyền riêng tư. Cùng với đó, người dùng sẽ có thể bỏ phiếu thuận hoặc chống lại các đề xuất mà không cần biết số phiếu bầu của từng người hoặc kết quả cho đến khi tất cả người dùng trong danh sách thành viên đã bỏ phiếu.

Tất nhiên, hạn chế quan trọng là người tham gia bỏ phiếu cuối cùng sẽ có thể giải mã và xem hướng đề xuất đang diễn ra trước khi bỏ phiếu và công bố phiếu bầu của họ.

2. Đặc điểm kỹ thuật

2.1. Luồng ứng dụng

Trước khi đi sâu vào phân tích kỹ thuật, điều quan trọng là phải xem xét bức tranh tổng quan và hiểu rõ quy trình ứng dụng cơ bản. Các quy trình tạo ví đa chữ ký, tạo đề xuất và thực hiện giao dịch đa chữ ký chung với biểu quyết đề xuất đều được cung cấp.

2.1.1. Tạo đa chữ ký

Nền tảng của ứng dụng là ví đa chữ ký. Khi tương tác với ứng dụng, người dùng tạo ví đa chữ ký với danh sách người được phép bỏ phiếu cho logic nghiệp vụ của họ.

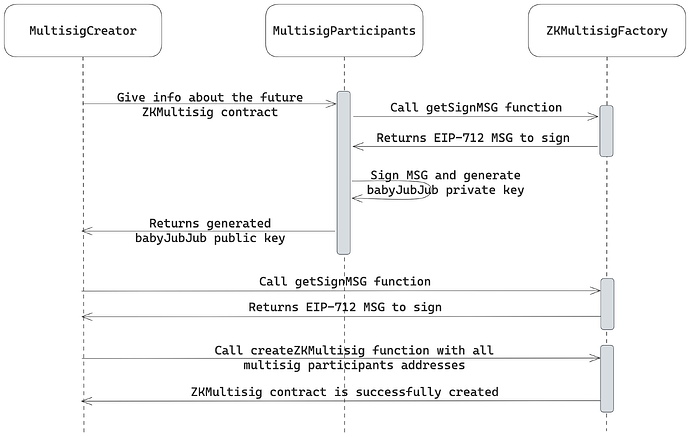
Luồng tạo đa chữ ký được mô tả trong sơ đồ sau:

Hình 1: Luồng tạo hợp đồng ZKMultisig 3159×2003 245 KB

1. Quy trình tạo ví bắt đầu bằng việc người dùng (người tạo ví) thu thập khóa công khai của người bỏ phiếu để thêm vào danh sách được phép. Vì đa chữ ký sử dụng ZK để duy trì quyền riêng tư, tất cả người dùng phải tạo một cặp khóa babyJubJub đặc biệt sẽ được sử dụng làm mã định danh duy nhất của họ trước khi sử dụng ứng dụng.

   Để tạo các khóa này, người dùng ký một thông điệp có cấu trúc EIP-712 bằng khóa riêng Ethereum (ECDSA) của họ và băm chữ ký thu được. Băm kết quả là khóa riêng babyJubJub.

   Người dùng có thể lựa chọn giữa việc ký các thông điệp duy nhất để có được khóa công khai duy nhất cho mọi chữ ký đa chữ ký mà họ muốn tham gia (tăng cường quyền riêng tư) hoặc sử dụng thông điệp "mặc định" để gắn bó với một khóa công khai duy nhất được sử dụng trên toàn nền tảng (có thể mang lại trải nghiệm người dùng tốt hơn).

2. Sau khi có được tất cả các khóa công khai babyJubJub cần thiết, người tạo ví sẽ kích hoạt chức năng tạo ví trên hợp đồng thông minh ZKMultisigFactory , cung cấp tất cả các khóa công khai cần thêm vào danh sách được phép. Bên trong, multisig lưu trữ danh sách người tham gia trong cấu trúc dữ liệu Sparse Merkle Tree (SMT), cho phép chứng minh tư cách thành viên bằng ZK và duy trì danh sách chi phí thấp.

3. Sau khi ví đa chữ ký được triển khai, các thành viên có thể tạo đề xuất và bỏ phiếu cho các đề xuất đó bằng cách tạo bằng chứng ZK về tư cách thành viên và áp dụng các biện pháp che mắt EdDSA để quyết định không thể tái sử dụng.

Với cách tiếp cận được mô tả, chúng ta có thể đạt được quyền riêng tư hoàn toàn cho người dùng bằng cách trừu tượng hóa "địa chỉ ví" thực của họ với một babyJubJub thông qua hàm phái sinh khóa xác định (KDF) và giảm xác suất xác định địa chỉ ra quyết định từ 1 xuống 1/N 1 / N , trong đó N N là số lượng thành viên đa chữ ký.

2.1.2 Tạo đề xuất

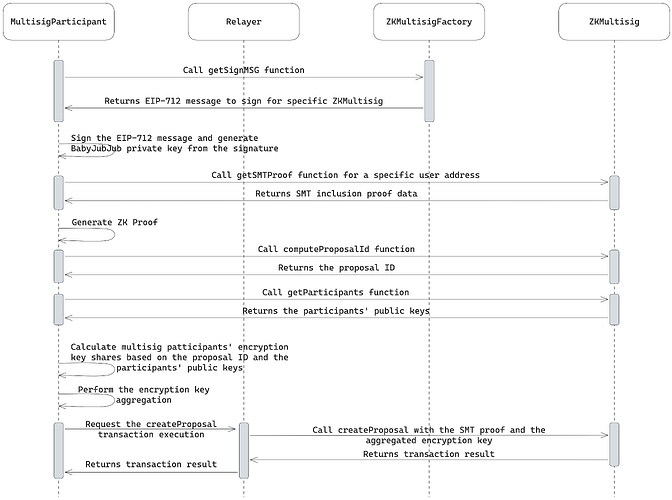
Luồng tạo đề xuất được mô tả trong sơ đồ bên dưới:

Hình 2: Luồng tạo đề xuất đa chữ ký 4360×3240 434 KB

1. Người tạo đề xuất (người dùng từ danh sách được phép đa chữ ký) đăng nhập vào ứng dụng bằng cách khôi phục cặp khóa babyJubJub một cách xác định từ bước "tạo ví đa chữ ký".

   Thuật toán KDF vẫn giữ nguyên. Thông điệp có cấu trúc EIP-712 được lấy từ ZKMultisigFactory , sau đó được ký và chữ ký được băm để tính toán khóa riêng babyJubJub.

2. Người dùng tạo bằng chứng ZK để xác minh tư cách thành viên của họ trong đa chữ ký mà không cần xin phép thông qua bằng chứng bao gồm SMT.

3. Người tạo đề xuất sẽ tính toán ID của đề xuất để sử dụng trong quá trình tạo khóa mã hóa tổng hợp một lần.

4. Người tạo tính toán không tương tác phần chia sẻ khóa mã hóa của mọi người tham gia đa chữ ký bằng KDF dựa trên ID đề xuất và khóa công khai babyJubJub của những người tham gia.

5. Sau khi tính toán tất cả các phần chia sẻ khóa mã hóa, người tạo sẽ tổng hợp chúng thành khóa mã hóa cuối cùng.

6. Người tạo đề xuất gọi hàm createProposal thông qua bộ chuyển tiếp, cung cấp bằng chứng bao gồm SMT và khóa tổng hợp để sử dụng cho việc mã hóa phiếu bầu.

Sau khi đề xuất được tạo, những người tham gia đa chữ ký có thể bắt đầu bỏ phiếu.

2.1.3. Biểu quyết về đề xuất

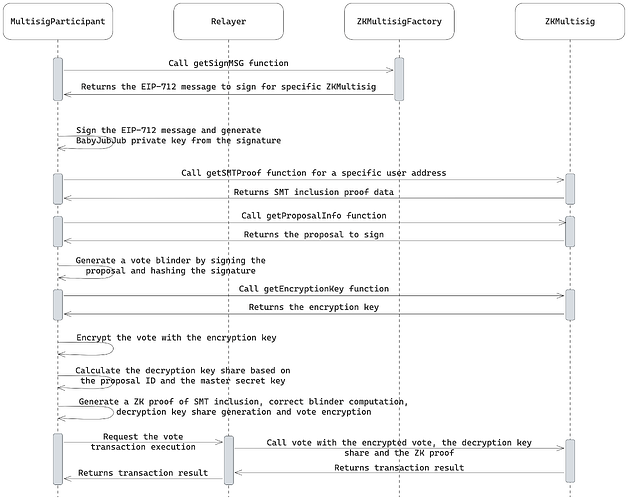
Quy trình bỏ phiếu cho đề xuất được mô tả trong sơ đồ sau:

Hình 3: Luồng bỏ phiếu đề xuất đa chữ ký 4120×3280 468 KB

1. Bằng chứng bao gồm SMT (Merkle) được lấy từ hợp đồng để chỉ ra rằng người dùng là thành viên của đa chữ ký.

2. Người dùng ký (bằng khóa riêng babyJubJub) vào đề xuất họ đang bỏ phiếu để tạo ra một mã mù bằng cách băm chữ ký EdDSA thu được. Mã này được sử dụng để xác minh rằng họ chưa từng bỏ phiếu cho cùng một đề xuất.

3. Người dùng lấy khóa mã hóa của đề xuất.

4. Khóa mã hóa tạm thời nhận được sẽ được sử dụng để mã hóa phiếu bầu của họ.

5. Dựa trên ID đề xuất, người dùng tính toán chia sẻ khóa giải mã bằng khóa riêng babyJubJub và KDF của họ.

6. Sau khi tính toán tất cả dữ liệu cần thiết, người tham gia đa chữ ký sẽ gọi chức năng vote thông qua bộ chuyển tiếp, cung cấp phiếu bầu được mã hóa, chia sẻ khóa giải mã và bằng chứng ZK.

7. Hợp đồng thông minh sẽ thêm khóa giải mã được cung cấp vào khóa giải mã cuối cùng có thể tổng hợp và thiết lập phiếu bầu thành công.

2.1.4 Công bố phiếu bầu và thực hiện đề xuất

Chỉ khi người tham gia cuối cùng đã bỏ phiếu, khóa giải mã mới hoàn tất và có thể được sử dụng để tiết lộ kết quả bỏ phiếu. Việc này được thực hiện bằng cách gọi hàm reveal . Hàm này sẽ giải mã các phiếu bầu tổng hợp và thay đổi trạng thái đề xuất theo kết quả bỏ phiếu. Nếu số phiếu "ủng hộ" vượt quá "ngưỡng chữ ký", đề xuất sẽ được đặt thành "chấp nhận" và có thể được thực thi, nếu không thì "bị từ chối".

Sơ đồ bên dưới minh họa quá trình tiết lộ phiếu bầu, gói gọn logic giải mã và thực thi vào một hàm duy nhất revealAndExecute .

Hình 4: Luồng tiết lộ phiếu bầu đề xuất đa chữ ký 2390×1540 169 KB

2.2. Toán mã hóa

Phần này cung cấp nền tảng toán học của logic mã hóa phiếu bầu được sử dụng trong giao thức.

2.2.1. Các phép toán trên đường cong Elliptic

Trong bối cảnh của tài liệu này, một số phép toán được thực hiện trên đường cong elip và liên quan đến các phép toán cụ thể khác với số học thông thường:

• Phép cộng điểm P + Q P + Q , trong đó P P và Q Q là các điểm trên đường cong elip, được thực hiện theo logic hoạt động nhóm đã xác định.
• Phép nhân vô hướng k \times P k × P , trong đó k k là một số vô hướng và P P là một điểm trên đường cong elip, bao gồm việc cộng điểm P P với chính nó k k lần.
• Phép trừ điểm P - Q P − Q , trong đó P P và Q Q là các điểm trên đường cong elip và giống hệt với P + (-Q) P + ( − Q ) , trong đó -Q − Q là điểm nghịch đảo của điểm Q Q .

2.2.2. KDF cho Khóa Mã hóa

Giao thức sử dụng lược đồ khóa ẩn CoM17 [1] làm KDF xác định. Lược đồ này cho phép tạo ra các chia sẻ khóa duy nhất để mã hóa và giải mã phiếu bầu cho mỗi đề xuất từ khóa chính.

Cặp khóa chính phải đáp ứng các yêu cầu sau:

pk = sk \times G, p k = s k × G ,

trong đó pk p k — khóa công khai chính,
sk s k — khóa bí mật chính,
G G — điểm cơ sở trên đường cong elip.

Cặp khóa babyJubJub được tạo trong quá trình tạo ví được sử dụng làm cặp khóa chính, từ đó các khóa mã hóa và giải mã ElGamal được suy ra. Quy trình suy ra khóa được mô tả bên dưới.

Đầu tiên, thử thách được tính toán dựa trên ID đề xuất. Lưu ý rằng đa chữ ký cố tình bỏ qua việc liệt kê gia tăng các đề xuất để ngăn chặn việc phát lại ZKP và các cuộc tấn công chạy trước. Điều này đạt được bằng cách yêu cầu người tạo đề xuất ký vào thử thách của đề xuất mà họ đang tạo. ID đề xuất và thử thách được tính toán một cách xác định như sau:

 proposalId = keccak256(abi.encode(target, value, data, salt));challenge = poseidon(uint248(keccak256(abi.encode(chainid, zkMultisigAddress, proposalId))));

Giả sử r r bằng với thử thách và R R là điểm thử thách:

R = r \times G R = r × G

Chia sẻ khóa mã hóa được lấy như sau:

P_i = poseidon(r \times pk_i ) \ times G + pk_i P i = poseidon ( r × p k i ) × G + p k i

Tương ứng, chia sẻ khóa giải mã được tính như sau:

x_i = (poseidon(sk_i \times R) + sk_i) \mod n x i = ( p o s e i d o n ( s k i × R ) + s k i ) bản mod N

trong đó n n — bậc của đường cong elip.

Tính nhất quán của sơ đồ suy luận khóa có thể được chứng minh bằng:

P_i = x_i \times G = (poseidon(sk_i \times R) + sk_i) \times G = P i = x i × G = ( p o s e i d o n ( s k i × R ) + s k i ) × G =
= poseidon(sk_i \cdot r \times G) \times G + sk_i \times G = poseidon(r \times pk_i) \times G + pk_i = p o s e i d o n ( s k i ⋅ r × G ) × G + s k i × G = p o s e i d o n ( r × p k i ) × G + p k i

2.2.3. Sơ đồ mã hóa ECC ElGamal

Giao thức sử dụng sửa đổi Mã hóa đường cong Elliptic (ECC) của lược đồ mã hóa ElGamal [2] để mã hóa và sau đó giải mã các phiếu bầu đa chữ ký.

Khóa mã hóa tổng hợp P P là một điểm trên đường cong elip được tính bằng cách cộng tất cả các phần khóa mã hóa:

P = \sum_{i=1}^N P_i, P = ∑ N i = 1 P i ,

trong đó N N — số lượng người tham gia đa chữ ký,
P_i P i — chia sẻ khóa mã hóa (điểm đường cong elliptic).

Phiếu bầu của người tham gia được ánh xạ đến một điểm M M trên đường cong elliptic. Điểm G G được sử dụng làm phiếu "thuận", và điểm ở vô cực làm phiếu "phản đối". Một giá trị ngẫu nhiên k k thỏa mãn 0<k<n 0 < k < n được chọn. Sau đó, bản mã ( C_1 C 1 , C_2 C 2 ) được tính toán:

C_1 = k \times G C 1 = k × G
C_2 = M + k \times P C 2 = M + k × P

Để giải mã phiếu bầu, trước tiên hãy tính toán tổng hợp chia sẻ khóa giải mã:

x = \sum_{i=1}^N x_i \mod n, x = ∑ N i = 1 x i bản mod N ,

trong đó n n — bậc của đường cong elip,
x_i x i — chia sẻ khóa giải mã (vô hướng).

Sau đó sử dụng khóa giải mã tổng hợp được tính toán x x để khôi phục điểm tin nhắn M M :

M = C_2 - x \times C_1 M = C 2 − x × C 1

Tính nhất quán của tổng hợp khóa trong lược đồ ECC ElGamal có thể được chứng minh như sau:

P = \sum_{i=1}^N P_i = \sum_{i=1}^N x_i \times G P = ∑ N i = 1 P i = ∑ N i = 1 x i × G

D = x \times C_1 = \sum_{i=1}^N x_i \times C_1 = \sum_{i=1}^N x_i \cdot k \times G = k \times (\sum_{i=1}^N x_i \times G) = k \times P D = x × C 1 = ∑ N i = 1 x i × C 1 = ∑ N i = 1 x i ⋅ k × G = k × ( ∑ N i = 1 x i × G ) = k × P

M = C_2 - D = M + k \times P - k \times P M = C 2 − D = M + k × P − k × P

2.2.4. Tổng hợp phiếu bầu đồng dạng

Sử dụng điểm G G và điểm vô cực làm phiếu bầu giúp có thể hình thành kết quả bỏ phiếu tích lũy một cách đồng dạng, tổng hợp các phiếu bầu được mã hóa trong mỗi lần bỏ phiếu:

SC_1 = \sum_{i=1}^N C_{1_i} S C 1 = ∑ N i = 1 C 1 i
SC_2 = \sum_{i=1}^N C_{2_i} S C 2 = ∑ N i = 1 C 2 i

Giải mã tổng để có được kết quả tổng hợp T T :

T = \sum_{i=1}^N M_i = SC_2 - x \times SC_1 T = ∑ N i = 1 M i = S C 2 − x × S C 1

Tổng giải mã T T bằng v \times G v × G , trong đó v v là tổng số cử tri đã bỏ phiếu “ủng hộ” đề xuất.

Để tiết lộ các phiếu bầu, người tham gia đa chữ ký phải lặp qua các giá trị vô hướng có thể có v_i v i ngoài chuỗi, trong đó 0 \leq v_i \leq N 0 ≤ v i ≤ N , để tìm giá trị thỏa mãn phương trình:

v_i \times G = T v i × G = T

Sau đó, họ gửi giá trị này tới hợp đồng thông minh, tại đó phương trình trên sẽ được kiểm tra.

• Nếu v < signaturesQuorum v < sign n a t u r e s Q u o r u m , không đủ số người tham gia bỏ phiếu “ủng hộ” đề xuất và trạng thái của đề xuất được đặt thành “bị từ chối”;
• Nếu v \geq signaturesQuorum v ≥ sign n a t u r e s Q u o r um , đủ số người tham gia đã bỏ phiếu “ủng hộ” đề xuất và trạng thái của đề xuất được đặt thành “đã chấp nhận”.

2.2.5. Tính toán khóa mã hóa trên chuỗi

Khi đề xuất được tạo, điều cần thiết là phải kiểm tra xem khóa mã hóa tổng hợp có được tính toán chính xác từ các khóa công khai riêng lẻ và thử thách hay không.

Vì giá trị này có thể tính toán công khai, nó có thể được đánh giá trên hợp đồng thông minh bằng cách lặp qua các khóa công khai chính của người tham gia và tính toán phần mã hóa của họ. Tuy nhiên, cách tiếp cận này chưa tối ưu và có thể được cải thiện bằng cách sử dụng một khóa công khai tích lũy, đại diện cho tổng các khóa công khai chính của tất cả người tham gia. Khóa này được lưu trữ trên hợp đồng thông minh và phải được cập nhật mỗi khi danh sách thành viên được cập nhật.

Thay vì tính toán chia sẻ khóa mã hóa cho từng người tham gia riêng lẻ:

P_i = poseidon(r \times pk_i ) \ times G + pk_i P i = poseidon ( r × p k i ) × G + p k i

Chỉ cần tính toán phần băm và thêm nó vào tổng các băm trước đó, giúp giảm số lượng thao tác bên trong vòng lặp:

sumHash = sumHash + poseidon(r \times pk_i) s u m H a s h = s u m H a s h + p o s e i d o n ( r × p k i )

Sau đó, khóa mã hóa tổng hợp có thể được tính toán như sau:

aggKey = sumHash \times G + cumulativePk a g g K e y = s u m H a s h × G + c u m u l a t i v e P k

2.3. Chức năng

Phần này cung cấp mô tả kỹ thuật về hợp đồng thông minh và mạch điện. Phần này cũng nêu rõ các chức năng cần thiết được các thành phần hỗ trợ để triển khai nguyên mẫu khả thi.

2.3.1. Nhà máy ZKMultisig

Có hai hợp đồng trong ứng dụng: ZKMultisigFactory và ZKMultisig . Nhà máy được sử dụng để tạo ví đa chữ ký và tạo các thông báo EIP-712 cần thiết cho quy trình tạo khóa. ZKMultisig là phần triển khai của chính ví.

Giao diện ZKMultisigFactory được định nghĩa như sau:

 interface IZKMultisigFactory {event ZKMultisigCreated(address indexed zkMultisigAddress,uint256[2][] initialParticipants,uint256 initialQuorumPercentage);function createZKMultisig(uint256[2][] calldata participants,uint256 quorumPercentage,uint256 salt) external returns (address);function computeZKMultisigAddress(address deployer,uint256 salt) external view returns (address);function getKDFMSGToSign(address zkMultisigAddress) external viewreturns (bytes32);function getDefaultKDFMSGToSign() external view returns (bytes32);function isZKMultisig(address multisigAddress) external view returns(bool);}

ZKMultisigFactory không triển khai ví trực tiếp, thay vào đó, các proxy ERC-1967 được triển khai. Hơn nữa, phương pháp create2 được áp dụng để cung cấp tính xác định cho địa chỉ ví nhằm thiết lập các thông điệp KDF ngay từ đầu.

Muối trong create2 được định nghĩa như sau:

 realSalt = keccak256(abi.encode(msg.sender, salt));

Người dùng có thể quyết định ký tin nhắn KDF nào:

• Tin nhắn duy nhất cho mỗi ví (tăng giả định về quyền riêng tư);
• Mặc định (có thể có UX tốt hơn).

Cấu trúc của các tin nhắn trả về có thể được tìm thấy ở phần 2.3.6.

2.3.2 ZKMultisig

ZKMultisig là một hợp đồng triển khai chức năng đa chữ ký. Việc triển khai bao gồm quản lý người tham gia đa chữ ký, thiết lập số lượng tối thiểu, tạo đề xuất, bỏ phiếu và thực hiện. Giao diện ZKMultisig được định nghĩa như sau:

 import "@solarity/solidity-lib/libs/data-structures/SparseMerkleTree.sol";interface IZKMultisig {enum ProposalStatus {NONE,VOTING,ACCEPTED,REJECTED,EXPIRED,EXECUTED}struct ZKParams {uint256[2] a;uint256[2][2] b;uint256[2] c;uint256[] inputs;}struct ProposalContent {address target;uint256 value;bytes data;}struct ProposalInfoView {ProposalContent content;ProposalStatus status;uint256 proposalEndTime;uint256 votesCount;uint256 requiredQuorum;}event ProposalCreated(uint256 indexed proposalId, ProposalContent content);event ProposalVoted(uint256 indexed proposalId, uint256 voterBlinder);event ProposalExecuted(uint256 indexed proposalId);function addParticipants(uint256[2][] calldata participantsToAdd) external;function removeParticipants(uint256[2][] calldata participantsToRemove) external;function updateQuorumPercentage(uint256 newQuorumPercentage) external;function create(ProposalContent calldata content,uint256 duration,uint256 salt,ZKParams calldata proofData) external returns (uint256);function vote(uint256 proposalId,bytes calldata encryptedVote,uint256 decryptionKeyShare,ZKParams calldata proofData) external;function reveal(uint256 proposalId, uint256 approvalVoteCount) external;function execute(uint256 proposalId) external;function revealAndExecute(uint256 proposalId,uint256 approvalVoteCount) external;function getPerticipantsSMTRoot() external view returns (bytes32);function getParticipantsSMTProof(bytes32 publicKeyHash)external view returns (SparseMerkleTree.Proof memory);function getParticipantsCount() external view returns (uint256);function getParticipants() external view returns (uint256[2][] memory);function getProposalsCount() external view returns (uint256);function getProposalsIds(uint256 offset, uint256 limit)external view returns (uint256[] memory);function getQuorumPercentage() external view returns (uint256);function getEncryptionKey(uint256 proposalId) external viewreturns (uint256[2] memory);function getProposalInfo(uint256 proposalId) external viewreturns (ProposalInfoView memory);function getProposalStatus(uint256 proposalId) external viewreturns (ProposalStatus);function getProposalChallenge(uint256 proposalId)external view returns (uint256);function computeProposalId(ProposalContent calldata content,uint256 salt) external view returns (uint256);function isBlinderVoted(uint256 proposalId,uint256 blinderToCheck) external view returns (bool);}

Điều quan trọng là phải xác minh việc tổng hợp khóa mã hóa ElGamal bên trong hàm createProposal cho đề xuất đã cho. Hợp đồng thông minh phải lặp qua các khóa công khai chính của các thành viên đang hoạt động, từ đó rút ra các khóa mã hóa chia sẻ của họ, sau đó được tổng hợp thành khóa mã hóa (xem phần 2.2.5).

2.3.3 Mạch tạo đề xuất

Mỗi tham số trong bài báo này được cung cấp với mục đích có thể chứng minh được và tương thích với các mạch không kiến thức. Danh sách các tín hiệu mạch để chứng minh đề xuất như sau:

Tín hiệu công cộng:

• Gốc SMT (đầu vào);
• ID đề xuất (đầu vào).

Tín hiệu riêng tư:

• Khóa bí mật chính;
• Khóa công khai chính [tùy chọn];
• Bằng chứng bao gồm SMT.

Khi sử dụng các tín hiệu này, mạch phải có những hạn chế sau:

• Khóa bí mật chính được cung cấp thực chất là khóa bí mật của khóa công khai chính được cung cấp.
• Khóa công khai chính thuộc về SMT, được neo vào gốc SMT.

2.3.4. Mạch bỏ phiếu đề xuất

Danh sách các tín hiệu mạch cho bằng chứng bỏ phiếu đề xuất như sau:

Tín hiệu công cộng:

• Người dùng bị che khuất (đầu ra);
• Chia sẻ khóa giải mã (đầu ra);
• Điểm mã hóa C_1 C 1 (đầu ra);
• Điểm mã hóa C_2 C 2 (đầu ra);
• Khóa mã hóa tổng hợp (đầu vào);
• Đề xuất thách thức (đầu vào);
• Gốc SMT (đầu vào).

Tín hiệu riêng tư:

• Khóa bí mật chính;
• Khóa công khai chính [tùy chọn];
• Chữ ký chính thức của EdDSA về thử thách;
• Phiếu bầu thực tế: điểm G G hoặc inf i n f ;
• Giá trị mã hóa ngẫu nhiên k k ;
• Bằng chứng bao gồm SMT.

Khi sử dụng các tín hiệu này, mạch phải có những hạn chế sau:

• Khóa bí mật chính được cung cấp thực chất là khóa bí mật của khóa công khai chính được cung cấp.
• Khóa công khai chính thuộc về SMT, được neo vào gốc SMT.
• Chữ ký chính EdDSA của thử thách sẽ được xác minh với khóa công khai chính.
• Băm Poseidon của chữ ký bằng với mã mù của người dùng.
• Chia sẻ khóa giải mã được tính toán chính xác dựa trên khóa bí mật chính và thách thức đề xuất (xem phần 2.2.2).
• Phiếu bầu được cung cấp có thể bằng G G hoặc inf i n f .
• Việc mã hóa đã được thực hiện chính xác khi cung cấp khóa mã hóa tổng hợp, giá trị mã hóa ngẫu nhiên k k và phiếu bầu (xem phần 2.2.3).

2.3.5. KDF

Hàm phái sinh khóa (KDF) là một hàm tạo ra khóa riêng babyJubJub một cách xác định từ một số dữ liệu đầu vào. Trong trường hợp này, dữ liệu đầu vào là chữ ký Ethereum ECDSA của thông điệp được định dạng EIP-712.

KDF được định nghĩa như sau:

 message = getKDFMSGToSign() or getDefaultKDFMSGToSign();signature = eth_signTypedData_v4(message);privateKey = keccak256(keccak256(signature));

Lưu ý rằng điều quan trọng là không bao giờ tiết lộ chữ ký vì khóa riêng tư xuất phát trực tiếp từ chữ ký.

2.3.6. Tin nhắn KD EIP-712

Để tạo thông điệp EIP-712 dẫn xuất khóa, một hàm băm kiểu thông điệp KDF được sử dụng, bao gồm địa chỉ ZKMultisig của hợp đồng. Điều này là đủ vì thông tin mạng và hợp đồng được bao gồm trong cấu trúc miền EIP-712 tiêu chuẩn.

 bytes32 KDF_MSG_TYPEHASH = keccak256("KDF(address zkMultisigAddr)");bytes32 kdfStructHash = keccak256(abi.encode(KDF_MSG_TYPEHASH, zkMultisigAddress));

Các hàm getKDFMSGToSign() và getDefaultKDFMSGToSign() tạo một thông báo EIP-712 như mô tả ở trên. Hàm getDefaultKDFMSGToSign() sử dụng địa chỉ số 0 để xây dựng thông báo mặc định.

2.3.7. Người chuyển tiếp

Vì phương pháp trên hoàn toàn độc lập với địa chỉ EVM mà giao dịch được gửi đi, người dùng có thể sử dụng các bộ chuyển tiếp khác nhau để bảo mật tính ẩn danh. Có thể sử dụng các bộ chuyển tiếp thân thiện với giao thức như GSN, tuy nhiên, điều này đòi hỏi logic tích hợp bổ sung ở phía giao diện người dùng.

3. Cơ sở lý luận

Bản sửa đổi ECC của lược đồ mã hóa ElGamal [2] được lựa chọn vì tính tương thích của nó với các hàm phái sinh khóa (KDF) và tổng hợp khóa. Bản chất không xác định của ElGamal, được giới thiệu bởi giá trị ngẫu nhiên k k , đảm bảo rằng mỗi hoạt động mã hóa tạo ra một bản mã duy nhất, giúp tăng cường bảo mật.

Để giảm thiểu rủi ro tập trung hóa liên quan đến việc quản lý khóa giải mã truyền thống, chẳng hạn như trong chương trình Chia sẻ Bí mật Shamir (SSS), trong đó yêu cầu phải có khóa giải mã trước khi chia sẻ bí mật, phương pháp Tạo Khóa Phân tán (DKG) đã được áp dụng. Phương pháp này cung cấp cơ chế tạo khóa giải mã theo cách phi tập trung bởi mọi bên tham gia, đảm bảo không bên nào sở hữu toàn bộ khóa trước khi tiết lộ.

Hầu hết các giao thức DKG loại bỏ nhu cầu về một bên đáng tin cậy bằng cách sử dụng Chia sẻ Bí mật Có thể Xác minh (VSS), yêu cầu sự tương tác của các bên tham gia để xác minh tính hợp lệ của chia sẻ. Quy trình này được thay thế bằng cách xác minh bằng chứng ZK về chia sẻ khóa giải mã theo yêu cầu khi bỏ phiếu.

Mặc dù DKG loại bỏ nhu cầu trao đổi khóa chia sẻ giữa các bên, nhưng nó vẫn yêu cầu công bố khóa chia sẻ mã hóa trong quá trình tạo đề xuất. Sử dụng KDF xác định, các bên tham gia có thể tránh các quy trình tương tác, cho phép người tạo đề xuất tổng hợp khóa mã hóa cuối cùng một cách không đồng bộ và độc lập.

4. Những cân nhắc và hạn chế về bảo mật

Có một số rủi ro và hạn chế về bảo mật vốn có trong giao thức cần được xem xét:

• Thiết lập tin cậy. Nếu Groth16 được sử dụng làm hệ thống kiểm tra zk-SNARK, cần phải thiết lập tin cậy cho từng mạch và phải được thực hiện đúng cách.

• Rò rỉ khóa riêng/chữ ký. Việc giữ bí mật khóa dẫn xuất chữ ký ECDSA là điều cần thiết. Cặp khóa babyJubJub được dẫn xuất trực tiếp từ khóa này, do đó, việc rò rỉ chữ ký sẽ khiến các chữ ký đa chữ ký (mà người dùng đang sử dụng) dễ bị tấn công lừa đảo/gửi thư rác.

• Chạy trước đề xuất. Mặc dù việc kiểm tra đề xuất được xác định dựa trên nội dung đề xuất, vẫn có thể chạy trước việc tạo đề xuất với một đề xuất giống hệt. Điều này không ảnh hưởng trực tiếp đến bảo mật, nhưng cần lưu ý.

• Bế tắc loại bỏ người tham gia. Nếu người tham gia bị loại bỏ không bỏ phiếu (điều này là bình thường đối với họ), đề xuất loại bỏ sẽ hết hiệu lực và người tham gia vẫn là thành viên đa chữ ký. Một giải pháp khả thi có thể là bỏ phiếu công khai về các đề xuất như vậy.

• Sửa đổi danh sách người tham gia. Việc thêm hoặc xóa người tham gia khỏi hệ thống đa chữ ký (multisig) sẽ rất khó khăn khi có các đề xuất đang hoạt động (đang diễn ra). Việc này có thể gây ra sự không nhất quán trong các khóa được sử dụng trong sơ đồ mã hóa. Một giải pháp khả thi là theo dõi các đề xuất đó và chỉ cho phép tạo ra chúng khi không có tiến trình nào khác.

• Lợi thế của người bỏ phiếu sau cùng. Vì việc giải mã phiếu bầu có thể thực hiện được khi tất cả các khóa giải mã được chia sẻ, nên người tham gia sau cùng có thể tái tạo các phiếu bầu trước đó trước khi bỏ phiếu của riêng mình.

• Khả năng mở rộng. Độ phức tạp của việc tính toán kết quả biểu quyết và đề xuất tăng theo số lượng người tham gia.

Tài liệu tham khảo

[1] Nicolas T. Courtois và Rebekah Mercer. Kỹ thuật quản lý khóa và địa chỉ ẩn trong
Hệ thống Blockchain. 2017. url: https://www.scitepress.org/papers/2017/62700/62700.pdf .
[2] Neal Koblitz. Hệ thống mật mã đường cong Elliptic. 1987. url: https://www.ams.org/journals/mcom/1987-48-177/S0025-5718-1987-0866109-5/S0025-5718-1987-0866109-5.pdf .