Chữ ký dựa trên hàm băm (Phần 1): Chữ ký dùng một lần

Tác giả: David Wong

Nguồn: https://www.cryptologie.net/posts/hash-based-signatures-part-i-one-time-signatures-ots/

Chữ ký Lamport

Vào ngày 18 tháng 10 năm 1979, Leslie Lamport đã công bố phát minh về chữ ký dùng một lần của mình.

Hầu hết các lược đồ chữ ký điện tử đều dựa vào các hàm một chiều, điển hình là các hàm băm, để chứng minh tính bảo mật. Sự tinh tế của lược đồ Lamport nằm ở chỗ chữ ký của nó chỉ phụ thuộc vào tính bảo mật của các hàm một chiều này.

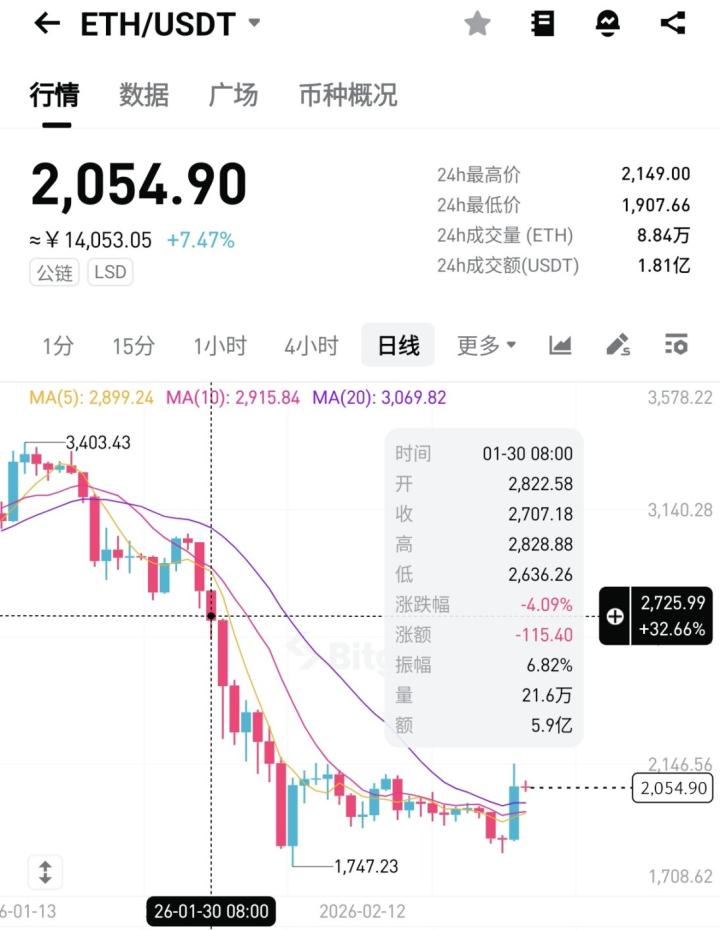
 (H(x) | H(y)) <-- 你的公钥(x, y) <-- 你的私钥

Lamport là một sơ đồ rất đơn giản. Đầu tiên, x và y đều là số nguyên. Khi gán dấu cho một bit đơn lẻ:

• Nếu giá trị của bit này là 0 , thì hãy giải phóng x
• Nếu giá trị của bit này là 1 , thì hãy công bố y

Rất đơn giản, phải không? Nhưng rõ ràng là bạn không thể ký nhiều lần bằng cùng một khóa công khai.

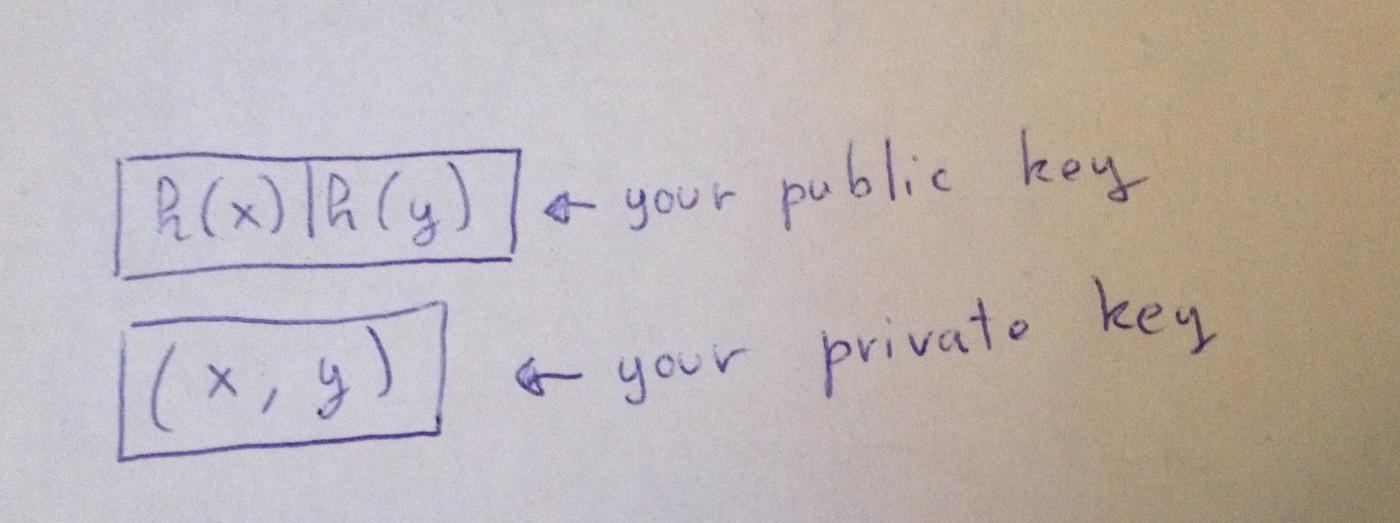
Vậy nếu bạn cần ký nhiều bit thì sao? Trước tiên, bạn có thể băm thông điệp cần ký, ví dụ, bằng cách đưa nó vào hàm băm SHA-256 (độ dài đầu ra của nó có thể dự đoán được, do đó xác định được độ dài của phần cần ký).

Bây giờ, (để ký 256 bit), bạn cần 256 cặp private key:

 (H(x_0) | H(y_0) | H(x_1) | H(y_1) | ... | H(x_255) | H(y_255)) <-- 你的公钥(x_0, y_0, x_1, y_1, ... x_255, y_255) <-- 你的私钥

Ví dụ, nếu bạn muốn ký 100110 , thì bạn cần công bố (y_0, x_1, x_2, y_3, y_4, x_5) .

Winternitz OTS (WOTS)

Vài tháng sau khi bài báo của Lamport được xuất bản, Robert Winternitz thuộc Khoa Toán học của Đại học Stanford đề xuất rằng $h^w(x)$ có thể được xuất bản thay vì $h(x) | h(y)$.

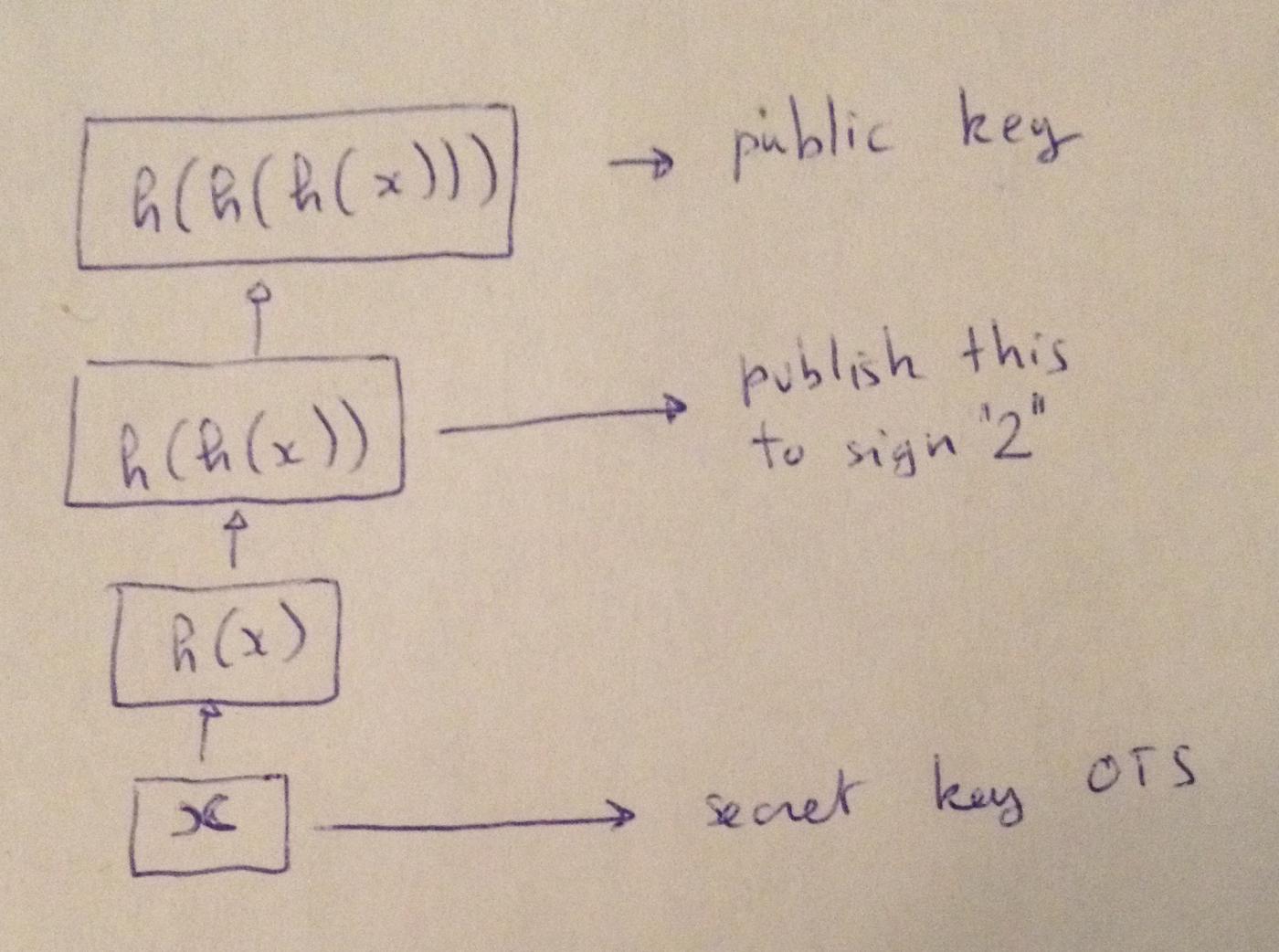
(Ghi chú của người dịch: Sử dụng một số nguyên x làm private key để ký một lần. Sử dụng H(x) để ký số 1 , sử dụng H(H(x)) để ký số 2 , v.v. Giả sử số lớn nhất bạn muốn ký là n , thì kết quả của việc băm x n + 1 lần liên tiếp chính là khóa công khai của bạn.)

Ví dụ, bạn có thể chọn $w = 16$ và công bố $h^{16}(x)$ làm khóa công khai của mình, chỉ cần lưu $x$ làm private key. Bây giờ, giả sử bạn muốn ký số nhị phân $1010$, tương ứng với $9$ trong hệ thập phân, bạn chỉ cần công bố $h^{9}(x)$.

Một vấn đề khác là kẻ xấu có thể nhìn thấy chữ ký này và băm nó; ví dụ, bằng cách băm lại, chúng có thể nhận được $h^{10}(x)$, tức là ngụy tạo chữ ký hợp lệ của bạn cho số nhị phân 1010 (hoặc số thập phân 10 ).

Một biến thể của chữ ký dùng một lần của Winternitz.

Mãi sau này, vào năm 2011, Buchmann và cộng sự đã công bố bản cập nhật cho chữ ký dùng một lần Winternitz, giới thiệu một biến thể: một nhóm các hàm nhận khóa làm đối số. Bạn có thể coi hàm này như một loại "mã xác thực thông điệp (MAC)".

Giờ đây, private key của bạn trở thành một tập hợp các khóa sẽ được sử dụng trong MAC, và thông điệp sẽ xác định số lần chúng ta lặp lại MAC này. Đây là một kiểu lặp đặc biệt vì đầu ra của lần lặp trước sẽ thay thế khóa được sử dụng trong hàm, và đầu vào chúng ta cung cấp cho hàm luôn giống nhau và là công khai. Hãy xem một ví dụ:

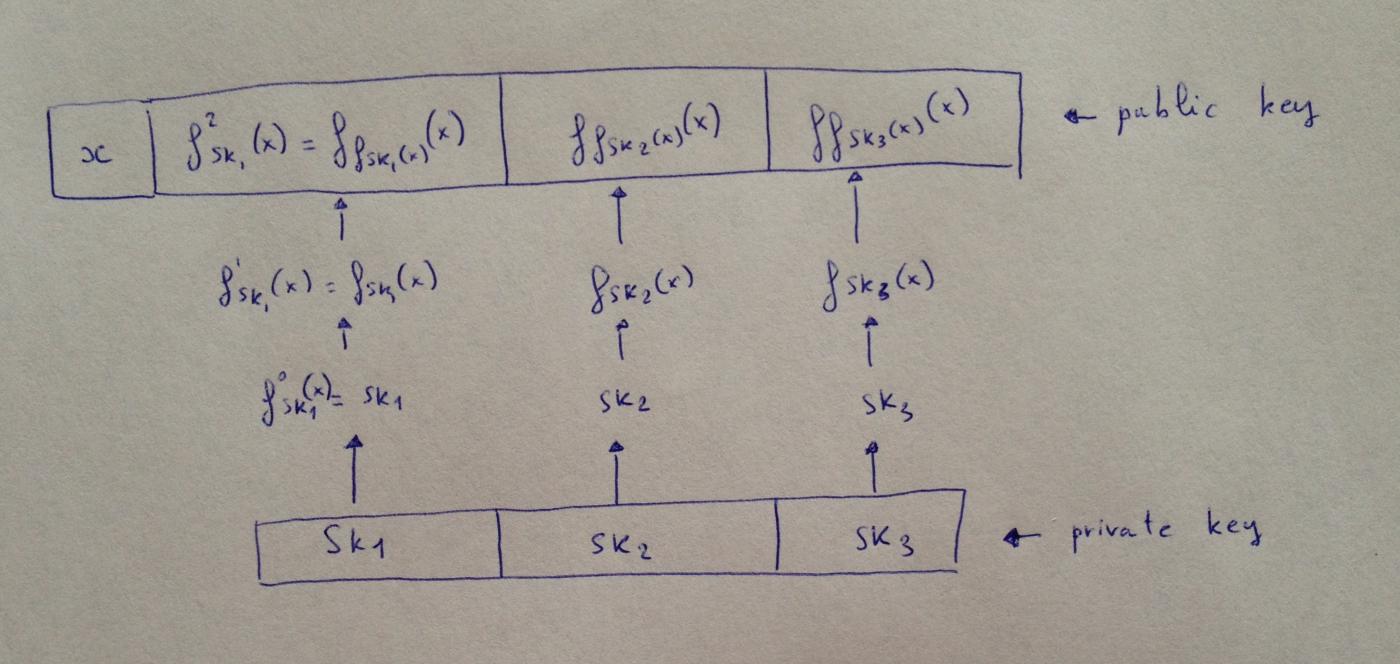
(Ghi chú của người dịch: Như thể hiện trong sơ đồ, trước tiên một khóa sk_i được tạo ra. Chữ ký cho giá trị 0 chính là sk_i . Sau đó, để ký các giá trị từ 1 trở lên, với bất kỳ sk_i nào, hàm được chạy một lần với sk_i làm tham số và x làm đầu vào; đây là một lần lặp. Giá trị thu được từ lần lặp này trở thành tham số cho lần lặp tiếp theo. x là một phần của khóa công khai và luôn được công khai.)

Thông điệp chúng ta cần ký là nhị phân 1011 , tương ứng với số thập phân 11 Giả sử biến thể W-OTS của chúng ta hoạt động với cơ số 3 (thực tế, nó hoạt động với bất kỳ cơ số w ). Do đó, chúng ta chuyển đổi thông điệp thành tam phân $M = (M_0, M_1, M_2) = (1, 0, 2)$.

Để ký thông điệp này, chúng ta chỉ cần công bố $(f_{sk_1}(x), sk_2, f^2_{sk_3}(x))$, trong đó mục cuối cùng là $f^2_{sk_3}(x) = f_{f_{sk_3}(x)}(x))$.

Xin lưu ý rằng có một điều tôi chưa đề cập ở đây, đó là thông điệp của chúng ta có một mã kiểm tra, và mã kiểm tra này cũng cần được ký. Đó là lý do tại sao việc chữ ký của $(M_2 = 2)$ đã bị lộ trong khóa công khai không quan trọng.

Trực giác mách bảo chúng ta rằng việc thêm một vòng lặp vào khóa công khai có thể mang lại tính bảo mật tốt hơn.

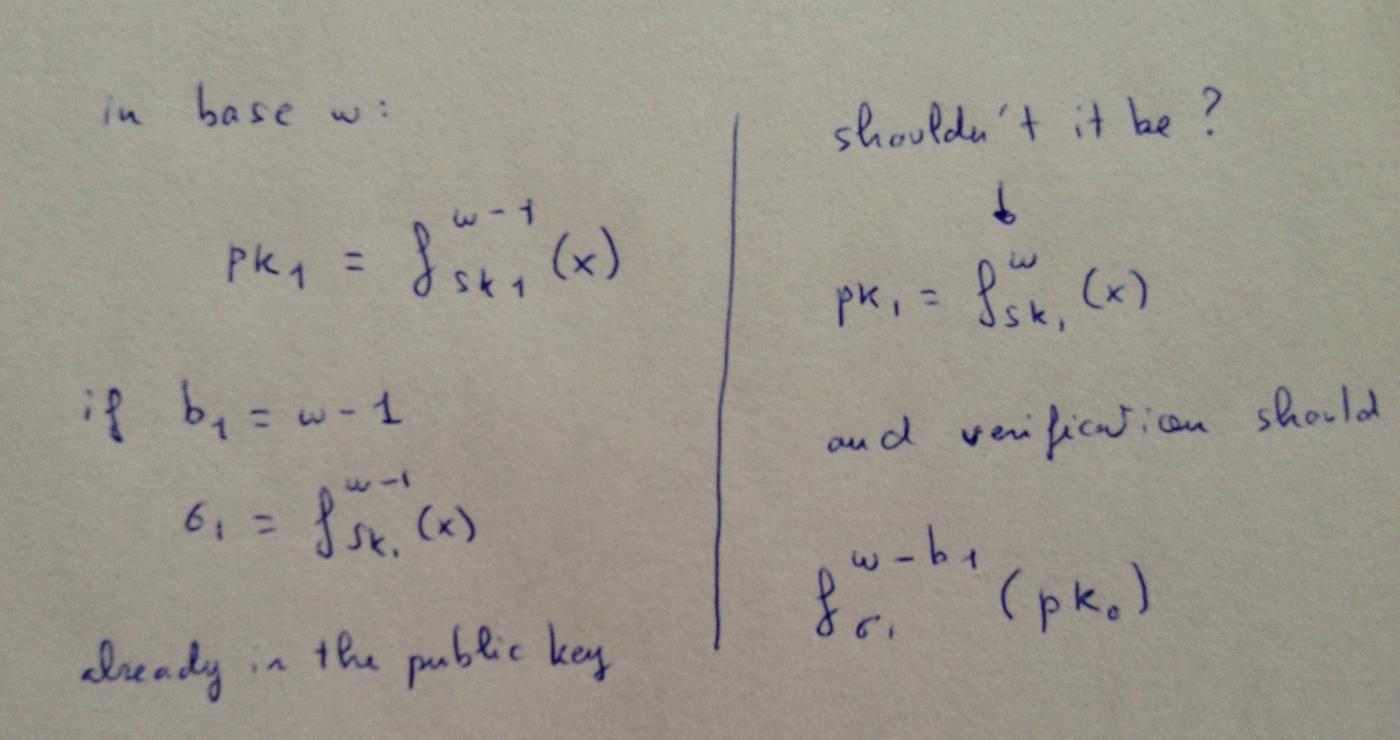
Sau đây là câu trả lời của Andres Hulsing cho câu hỏi của tôi trong bài thuyết trình của ông về chủ đề này :

Tại sao? Lấy bit 1 làm ví dụ: tổng kiểm tra sẽ là 0. Do đó, để ký thông điệp này, bạn chỉ cần biết ảnh ngược của một phần tử khóa công khai. Để phương pháp này an toàn, độ khó của nó phải tăng trưởng theo cấp số nhân với tham số bảo mật. Việc yêu cầu kẻ tấn công có thể đảo ngược hàm băm trên hai giá trị, hoặc đảo ngược nó lần trên cùng một giá trị, chỉ làm tăng độ phức tạp của cuộc tấn công lên gấp đôi. Điều này không làm tăng đáng kể tính bảo mật của phương pháp. Từ góc độ bảo mật bit, bạn chỉ có thể đạt được thêm 1 bit bảo mật (với chi phí là tăng gấp đôi thời gian chạy).

(Ghi chú của người dịch: "Bảo mật bit" đo lường lần tấn công vét cạn cần thiết để phá vỡ một hệ thống. Ví dụ, "bảo mật 80 bit" có nghĩa là bạn cần thực hiện 2^ lần lần tìm kiếm.)

Winternitz OTS+ (WOTS+)

Không có nhiều điều để nói về lược đồ W-OTS+. Hai năm sau khi biến thể nói trên xuất hiện, Hulsing đã độc lập công bố một nâng cấp giúp rút ngắn kích thước chữ ký và cải thiện tính bảo mật. Ngoài nhóm các hàm lấy khóa làm tham số, nó còn sử dụng một hàm chuỗi. Trong lược đồ được cập nhật, khóa vẫn giữ nguyên trong mỗi lần lặp; chỉ có đầu vào trở thành đầu ra của lần lặp trước. Hơn nữa, trước khi áp dụng hàm một chiều cho đầu ra trước đó, nó được XOR với một giá trị ngẫu nhiên (hoặc "mặt nạ").

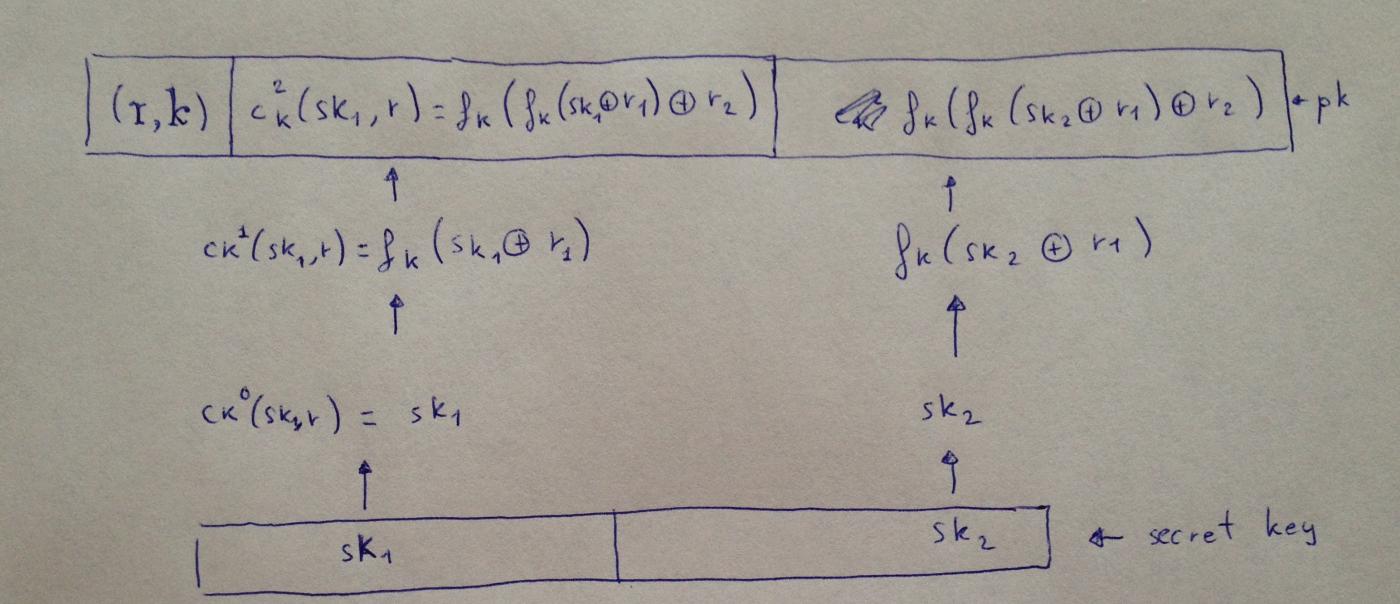
Mô tả chính xác về chữ ký rút gọn từ Hulsing:

WOTS+ có thể rút ngắn kích thước chữ ký vì bạn có thể sử dụng hàm băm ngắn hơn (so với các biến thể WOTS khác có cùng mức độ bảo mật hoặc chuỗi băm dài hơn). Nói cách khác, nếu cùng một hàm băm, cùng độ dài đầu ra và cùng tham số Winternitz w được sử dụng cho tất cả các biến thể WOTS, thì WOTS+ có thể đạt được mức độ bảo mật cao hơn các biến thể khác. Điều này rất quan trọng bởi vì, ví dụ, nếu bạn muốn sử dụng hàm băm 128 bit — đừng quên rằng WOTS gốc yêu cầu hàm băm phải chống va chạm, nhưng biến thể năm 2011 của chúng tôi và WOTS+ chỉ yêu cầu hàm giả ngẫu nhiên/hàm băm chống tìm ảnh ngược thứ hai — trong trường hợp này, WOTS gốc chỉ có thể đạt được mức độ bảo mật 64 bit, điều này có thể được coi là không an toàn. Đề xuất năm 2011 của chúng tôi và WOTS+ có thể đạt được mức độ bảo mật 128 - f(m, w) bit. Về sự khác biệt giữa hai phiên bản sau, trong WOTS-2011, f(m, w) tăng tuyến tính với w ; Trong khi đó, ở WOTS+ f(m, w) tăng trưởng tuyến tính với w. Nó thể hiện tăng trưởng theo hàm logarit.

Các OTS khác

Bài đăng trên blog hôm nay đến đây là kết thúc! Tuy nhiên, vẫn còn nhiều hình thức chữ ký dùng một lần khác. Nếu bạn quan tâm, đây là danh sách, một số trong đó vượt qua chữ ký dùng một lần vì chúng có thể được sử dụng lại với số lượng nhỏ. Vì vậy, chúng ta có thể gọi chúng là "Hình thức chữ ký ít lần (FTS)":

• 1994, The Bleichenbacher-Maurer OTS
• 2001, The BiBa OTS
• 2002, HORS
• 2014, HORST (Ngựa với Cây)

Cho đến nay, các ứng dụng dường như đã thu hẹp lại thành các chữ ký dựa trên hàm băm, vì đây là các lược đồ chữ ký hiện được khuyến nghị cho bảo mật hậu lượng tử. Xem " Các khuyến nghị sơ bộ về mật mã hậu lượng tử", được xuất bản vài tháng trước.

Ngoài ra: Xin cảm ơn Andreas Hulsing về bình luận.

Xem phần tiếp theo tại đây.