我们在此总结了首次对不活动泄漏进行理论分析的文章,该分析旨在在灾难性网络故障期间恢复最终确定性。这项工作已被 DSN2024 接受。
总结
- 不活动泄漏本质上对协议的安全性是有问题的。它有利于不断完成区块(活跃度),但代价是产生冲突的最终区块(安全性)。
- 拜占庭验证者(偏离协议的验证者)的存在会加速安全性的丧失。
以太坊 PoS 区块链致力于实现最终链的持续增长。因此,该协议激励验证者积极地完成区块。不活动泄漏是用于重新获得最终性的机制。具体来说,如果一条链连续四个时期没有完成最终确定,就会引发不活动泄漏。不活动泄漏于 2023 年 5 月首次在主网上发生。
感谢 Ben Eddington 的出色工作(这激发了本文的创作),我们在这里对不活动泄漏进行了很好的介绍。我们从不活动分数开始正式化不活动泄漏。
不活跃分数
在不活动泄漏期间,在时期t t ,验证器i i的不活动分数I_i(t) I i ( t )为:
因此,如果验证者处于不活跃状态,其不活跃分数将增加4 4 ,如果处于活跃状态,其不活跃分数将减少1 1。不活跃分数始终为正,并将用于在不活跃泄漏期间惩罚验证者。
不活动惩罚
令s_i(t) s i ( t )表示验证者i i在时期t t的质押,令I_i(t) I i ( t )表示其不活跃分数。每个时期t t 的惩罚为I_i(t-1)\cdot s_i(t-1)/2^{26} I i ( t − 1 ) ⋅ s i ( t − 1 ) / 2 26 。因此,质押的演变表示为:
不活动泄漏期间的质押
在本研究中,我们将权益函数s建模为连续可微函数,得到以下微分方程:
通过这个等式,我们可以通过固定其不活跃分数的演变来确定验证者随着时间的推移所获得的权益。这正是我们所做的。我们定义了两种类型的行为:活跃和不活跃。
- 活跃验证者:他们始终处于活跃状态。
- 不活跃的验证者:他们总是处于不活跃状态。
具有这些行为的验证者的不活跃分数会经历不同的演变:(a)活跃验证者的不活跃分数为常数I(t)=0 I ( t ) = 0 ;(b)不活跃验证者的不活跃分数每个时期增加 4, I(t)=4t I ( t ) = 4 t 。不活跃泄漏期间每种类型的验证者的权益:
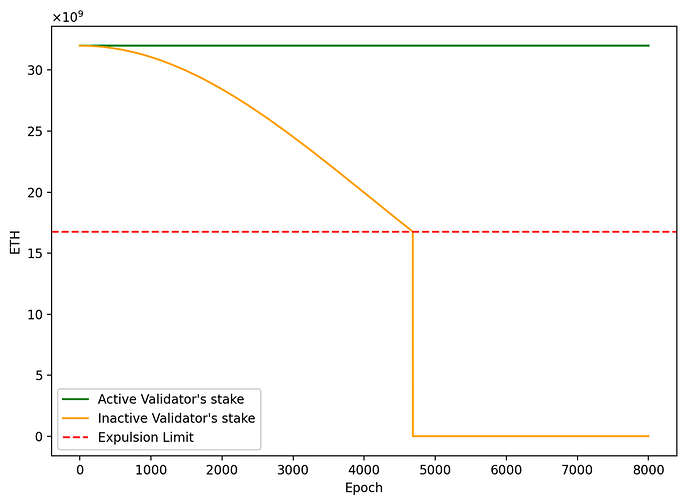
- 活跃验证者的权益: s(t) = s_0 = 32. s ( t ) = s 0 = 32.
- 不活跃验证者的权益: s(t) = s_0e^{-t^2/2^{25}}. s ( t ) = s 0 e − t 2 / 2 25 。
该图显示了验证者在不活动泄漏期间根据其活动而变化的权益。协议设置了驱逐限制,以驱逐累积过多惩罚的验证者。
什么是活跃验证者?
这是一个重要的细节;活动实际上取决于链。这意味着不同的链对同一验证者将有不同的不活动分数。因此,验证者可以从链中被逐出,而不会在另一条链上丢失 wei。
这是协议的形式化。现在我们对协议的安全性进行分析。为此,我们使用以下模型。
模型
- 网络:我们假设一个部分同步系统,它在先验未知的全局稳定时间(GST)之后从异步状态转换到同步状态。
- 错误:验证者要么诚实,要么拜占庭(偏离协议)。拜占庭验证者可以任意偏离协议。
- 质押:每个验证者初始质押 32 ETH。
异步状态下消息传输延迟没有限制。
安全出发
只有诚实的验证者
根据构造,如果分区持续足够长的时间,不活动泄漏将破坏安全性。问题是,速度有多快?
任何持续时间超过 4686 个 epoch(约 3 周)的网络分区都将因最终确定冲突而导致安全性损失。这是在只有诚实验证者的情况下,不活动泄漏持续时间的安全性上限。
详细分析
让我们分析一下验证者(都是诚实的)被分成两部分的场景。(根据我们的模型,我们处于异步状态)。
分区必然会产生分叉,每个分区都建立在它们看到的唯一一条链上。一旦活跃验证者的比例恢复到 2/3,链就会最终确定。
在这种情况下,通过了解验证者在各个分区的分布情况,我们可以计算出活跃验证者的权益比例返回到每个分支上权益的 2/3 所需的时间,从而最终确定并打破安全性。
为了进行分析,我们做了以下标记。在不活动泄漏的开始:
- n n是验证者的总数
- n_B n B是拜占庭验证者的总数
- n_H n H是诚实验证者的总数
- n_{H_1} n H 1是分支 1 上的诚实验证者的数量
- n_{H_2} n H 2是分支 2 上的诚实验证者的数量
在我们分析的第一部分中,没有拜占庭验证者,这意味着n=n_H n = n H 。诚实验证者仅分为两部分,因此n_H=n_{H_1}+n_{H_2} n H = n H 1 + n H 2 。
我们的目标是确定分支 1 上的诚实验证者比例何时会超过总权益的 2/3。也就是说,我们查看以下比例:
优于 2/3。使用我们的符号,该比率可以重写为:
s_{\text H_1} s H 1和s_{\text H_2} s H 2分别是诚实的活跃和非活跃验证者的赌注。由于分支 1 上的n_{\text H_1} n H 1 个验证者始终在分支 1 上活跃,而n_{\text H_2} n H 2 个验证者始终在分支 1 上非活跃(它们在分支 2 上活跃);我们知道s_{\text H_1}(t)=s_0 s H 1 ( t ) = s 0和s_{\text H_2}(t)=s_0e^{-t^2/2^{25}} s H 2 ( t ) = s 0 e − t 2 / 2 25 。
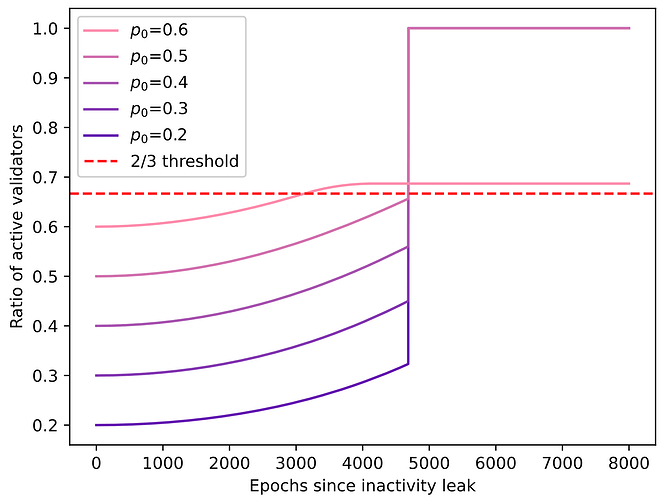
使用符号p_0=n_{\text H_1}/n_H p 0 = n H 1 / n H ,活跃验证者随时间的比例为:
此图显示了分支 1 上活跃验证者随时间的变化比例。如果到t= 4685时代还没有完成,则非活跃验证者将被剔除,从而导致活跃验证者比例跃升至 100%。
拜占庭验证者
我们现在添加了拜占庭验证器。
这些拜占庭验证器可以不受限制地向每个分区发送消息。
这看起来似乎有点过度,但这是分布式系统中赋予拜占庭更多权力的传统假设。提出 ETH2 协议的Gasper 论文在其模型中大量引用了PBFT 论文。以下是 PBFT 论文中的一句话: “我们允许一个非常强大的对手,它可以协调故障节点、延迟通信或延迟正确节点,以对复制服务造成最大的损害。”
我们的假设不太成立。想象一下欧洲和美国之间的通信被切断,但每个地区内部的通信仍然正常的情况。根据我们的模型,我们假设拜占庭验证者可以不受限制地与两个地区进行通信,就好像他们有自己的跨地区通信方式一样。
现在我们分析的情况是这样的:
- 不到三分之一的股权由拜占庭验证者持有( \beta_0=n_{\rm B}/n<1/3 β 0 = n B / n < 1 / 3 )。
- 诚实验证者被分为分支1 1和2 2 ;分支1 1 上的比例为 p_0=n_{\rm H_1}/n_{\rm H} p 0 = n H 1 / n H ,分支 2 2 上的比例为 1 - p_0=n_{\rm H_2}/n_{\rm H} 1 − p 0 = n H 2 / n H 。
- 拜占庭验证者可以与两个分支进行通信。
拜占庭验证者可以同时在两个分支上活跃,从而更快地破坏安全性。分支 1 上的活跃验证者比例为:
下表显示了根据拜占庭验证者的初始比例( \beta_0 β 0 )打破安全性所需的时间: 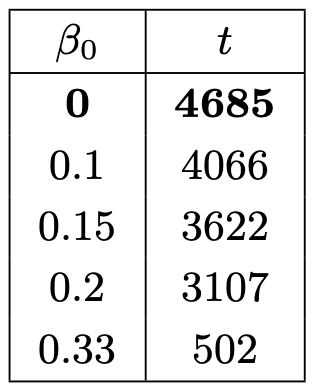
拜占庭验证者可以加速安全性的丧失。如果他们的初始比例为 0.33,他们可以使冲突的最终确定发生速度比只有诚实参与者的场景快大约十倍。
原始论文提供了有关假设、场景、协议和其他方面的更多细节,例如:
- 拜占庭验证者在不实施可削减行为的情况下破坏安全性的方法。
- 拜占庭验证者在分叉的两个分支上超过 1/3 阈值的方法。
- 考虑不活动泄漏时对概率弹跳攻击的分析。剧透警告:这会稍微加剧攻击,但攻击开始和持续的条件使其不太可能成为真正的威胁。
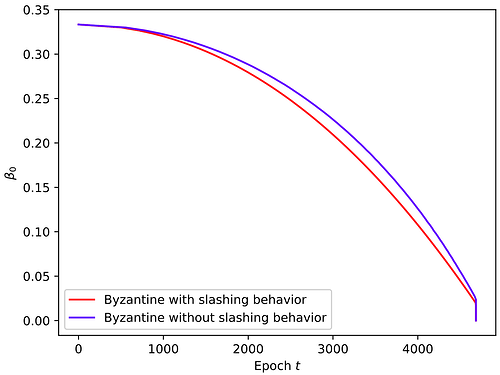
为了进一步快速了解该论文的研究结果,这里有一张图表,展示了拜占庭验证者根据其初始比例以及其行为是否可削减而破坏安全性的速度。如您所见,即使没有可削减行为,它们也会产生很大的影响。
结论
我们的研究结果强调了惩罚机制在拜占庭容错 (BFT) 分析中的重要性。通过识别协议设计中的潜在问题,我们旨在为未来的改进提供见解,并为进一步调查提供工具。