在这篇文章中,我们将分析发行曲线的形状对验证者集去中心化的影响。
行动过程如下:
首先,我们将引入有效收益率的概念,即考虑发行所产生的稀释后观察到的收益率。
其次,我们将引入实际收益率的概念,即验证者获得后期费用(营运支出、资本支出、税收…)的有效收益率。
有了这些定义,我们将能够对发行曲线的形状如何导致中心化力量进行一些观察,因为观察到的实际收益率可以以高权益率驱逐小型不相关的权益持有者。
然后,我们将提出一些我们期望发行曲线满足的属性,以最大限度地减少这些中心化力量。并探索一些可以解决上述问题的替代发行曲线。
最后,关于如何确定发行和殖利率曲线的具体选择的一些启发性论点。
所有图的源代码可以在这里找到: GitHub - pa7x1/ethereum-issuance
有效产量
有效收益率是指以太坊持有者在考虑流通供应变化后观察到的收益率。例如,如果每个人都成为质押者,那么观察到的收益率实际上将是 0%。由于新发行的股票在所有参与者之间平均分配,因此每个质押者所经历的流通供应的所有权不会改变。扣除税前和其他相关成本,这种情况更像是代币重新计价或部分股票分割。因此,我们预期随著权益率成长至 100%,有效收益率将逐步达到 0%。
另一方面,非质押持有者正在被新发行的股票稀释。这导致持有者因发行而经历负的有效收益率。我们预计,随著权益率越来越接近 100%,这种影响会越来越严重。
这些想法可以用数学术语非常简单地表达。
我们称s为权益持有者持有的 ETH 数量, h h称为非权益持有者(持有者)持有的 ETH 数量, t称为总流通供应量。然后:
s + h = t s + h = t
质押一定时间后,我们会达到一个新的情况s' + h' = t' s ' + h ' = t ' 。其中s' s '和t' t '因新发行i i而被夸大,显然与名义质押收益率y_s y s相关:
s' = s + i = s \cdot y_s s ′ = s + i = s ⋅ y s
h' = h h ′ = h
t' = t + i = t + s \cdot (y_s - 1) t ′ = t + i = t + s ⋅ ( y s − 1 )
现在,我们来介绍归一化量s_n s n和h_n h n 。它们只是代表每个子集代表的总流通供应量的比例:
s_n \equiv \frac{s}{t} s n ≡ s t
h_n \equiv \frac{h}{t} h n ≡ h t
我们可以对s'_n s ′ n和h'_n h ′ n执行相同的操作:
s'_n \equiv \frac{s'}{t'} = \frac{sy_s}{s(y_s - 1) +t} s ′ n ≡ s ′ t ′ = y s s ( y s − 1 ) + t
h'_n \equiv \frac{h'}{t'} = \frac{ts}{s(y_s - 1) + t} h ′ n ≡ h ′ t ′ = t − s s ( y s − 1 ) + t
有了这些定义,我们现在可以将有效收益率引入为每个子集观察到的总循环供应量比例的变化。
y_s^{eff} \equiv \frac{s'_n}{s_n} = \frac{y_s}{\frac{s}{t}(y_s-1) + 1} y e f f s ≡ s ′ n s n = y s s t ( y s − 1 ) + 1
y_h^{eff} \equiv \frac{h'_n}{h_n} = \frac{1}{\frac{s}{t}(y_s-1) + 1} y e f f h ≡ h ′ n h n = 1秒( y s − 1 ) + 1
净收益
质押有相关成本。质押者必须购买一台消费级 PC,必须支付一定金额(尽管很小)的电费,必须具有高速网路连线。他们还必须投入自己的劳动力和时间来维护系统的运作和安全,或者必须花钱请人为他们做这项工作。质押者也观察到其他形式的成本,这些成本会侵蚀他们观察到的名目报酬率,例如税收。我们希望对所有形式的成本后观察到的净收益率进行建模,因为它可以为我们提供有价值的信息,了解名义权益收益率的变化如何影响不同的利害关系人。
为了对此进行建模,我们将引入两种类型的成本;与名目收益成比例的成本(例如,LST 收取的税费或费用适合此范围),以及不随名目收益而变化的成本(即硬体、电力、网路、劳动力…)。
根据我们的定义,在一个参考周期的质押后,质押者将获得s' = y_s s = s + s(y_s - 1) s ′ = y s s = s + s ( y s − 1 )
但是,如果我们引入侵蚀名目殖利率的成本(让我们称之为k k ),以及侵蚀本金的成本(让我们称之为c c )。我们得到以下净权益公式:
s' = s(1-c) + s(y_s - 1) - \max(0, sk(y_s - 1)) s ′ = s ( 1 − c ) + s ( y s − 1 ) − max ( 0 , sk ( y s − 1 ) )
注意:最大值只是防止在收益率变成负数时,与收益率成比例的成本变成利润。例如,如果收益率变成负值,LST 不太可能向 LST 持有者支付 10%。或者,如果收益率为负,您可能无法像负收入一样收回税款。在这些情况下,我们将其设为 0。
这代表了我们的质押者在考虑所有形式的成本后所观察到的净质押。需要注意的是,这个公式可以很容易地修改以考虑其他类型的影响,例如验证器有效性(充当项(y_s - 1) ( y s − 1 )的乘法因子)或相关/反相关激励(其中改变y_s y s )。
为了确定想法,我们来估计 3 种不同类型的质押者观察到的净收益。家庭质押者、LST 持有者、机构大型业者。提议的价值观仅具有方向性,应进行调整以最好地反映每个利害关系人的现实。
家庭抵押者必须支付 5 年摊提的 PC 费用,成本约为 1000 美元,即每年 200 美元。网路费用为每月 50 美元,每年约 600 美元。额外的电费,典型的 NUC 每年不到 100 美元。假设他们是业余爱好者,并决定利用业余时间来做这件事,将他们的时间估价为 0 美元/年。这意味著他的质押操作每年将为他们带来约 1000 美元的成本。如果他们有 32 个 ETH,以当前 ETH 价格,我们可以将其四舍五入为约 10 万美元。这表示对于该抵押者, c = \frac{1}{1000} c = 1 1000 。因为他们的成本约为其股票价值的千分之一。
现在让我们来看看与产量成正比的成本。他们必须纳税,这在很大程度上取决于其税收管辖权,但在大多数已开发国家可能在 20% 到 50% 之间变化。我们选择 35% 作为中间值。在这种情况下,扣除成本后他们的股份如下:
s' = s\left(1-\frac{1}{1000}\right) + s(1-0.35)(y_s - 1) s ′ = s ( 1 − 1 1000 ) + s ( 1 − 0.35 ) ( y s − 1 )
我们可以使用 LST 为质押者做同样的练习。在这种情况下, c=0 c = 0 , k k由质押费用(10-15%)和税收(20-50%)组成,取决于税务处理。重新定基代币的优点是延迟资本利得的实现。如果我们假设持有期间为 5 年,相当于我们假设的单独质押的摊销时间,则可能如下所示:
- 固定成本:0
- 质押费用:10%
- 资本利得税:20%
- 持有期限:5年
s' = s(1-0) + s(1-0.14)(y_s - 1) s ′ = s ( 1 − 0 ) + s ( 1 − 0.14 ) ( y s − 1 )
最后,对于大型营运商。他们有更高的固定成本,他们将不得不支付人工费用等……但也会运行更多数量的验证器。在这种情况下,c 可以变得小得多,因为它是 s 的一部分。也许小 1 或 2 个数量级。税收将是典型的公司税率(20-30%)。
s' = s\left(1-\frac{1}{10000}\right) + s(1-0.25)(y_s - 1) s ′ = s ( 1 − 1 10000 ) + s ( 1 − 0.25 ) ( y s − 1 )
净有效收益率(又称实际收益率)
最后,我们可以将这两个概念融合在一起,以了解质押者或持有者在扣除所有形式的成本后以及供应变化稀释后获得的实际收益是多少。我建议将此净有效收益率称为实际收益率,因为这就是您真正获得的收益率。
y_s^{实数} = \frac{(1-c) + (y_s - 1) - \max(0,k(y_s - 1))}{\frac{s}{t}(y_s-1)+1 } y real s = ( 1 − c ) + ( y s − 1 ) − max ( 0 , k ( y s − 1 ) ) s t ( y s − 1 ) + 1
y_h^{real} = y_h^{eff} = \frac{1}{\frac{s}{t}(y_s-1) + 1 } y real h = y e f f h = 1 s t ( y s − 1 ) + 1
在第二个方程中,我们只是简单地说明持有没有成本的事实,因此持有的实际收益率(扣除成本后)与持有的有效收益率相同。
发行曲线和集中化
到目前为止,提出的所有方程式都与以太坊的特殊性无关,实际上同样适用于利害关系人观察到收益率但该收益率来自新发行的任何其他场景。
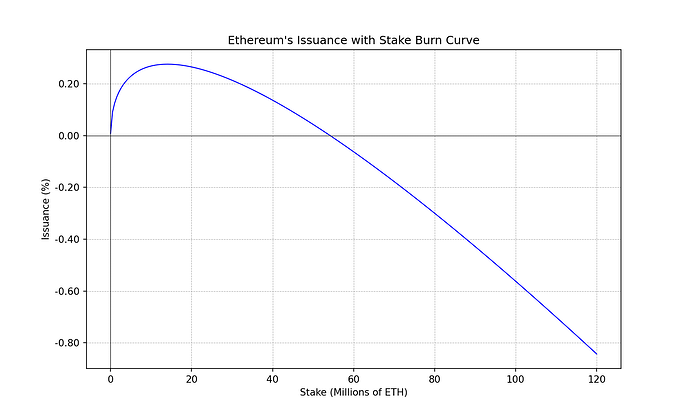
为了将此分析带回以太坊领域,只需用以太坊的发行收益率(作为质押总额s的函数)代替y_s y s 。并将t t替换为 ETH 的总流通供应量。
t \约 120\cdot 10^6 \quad \text{ETH} t ≈ 120 ⋅ 10 6以太坊
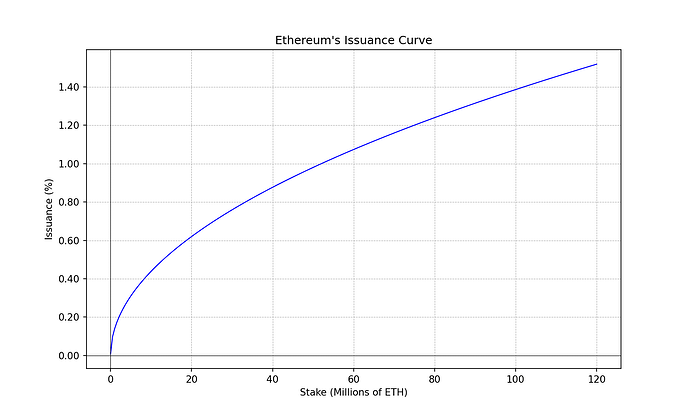
i(s) = 2.6 \cdot 64 \cdot \sqrt{s} \quad \text{ETH}\cdot\text{年份}^{-1} i ( s ) = 2.6 ⋅ 64 ⋅ √ s ETH ⋅年− 1
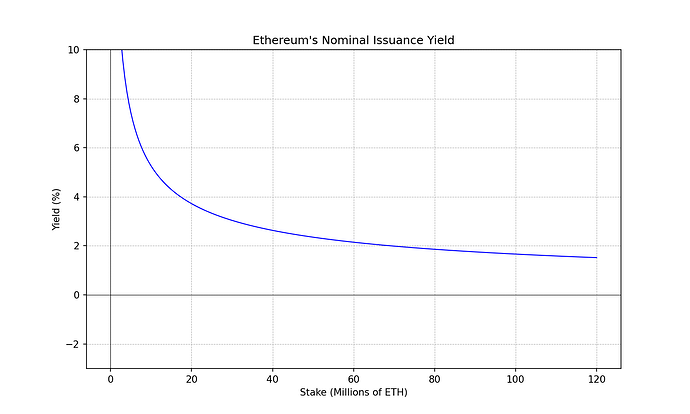
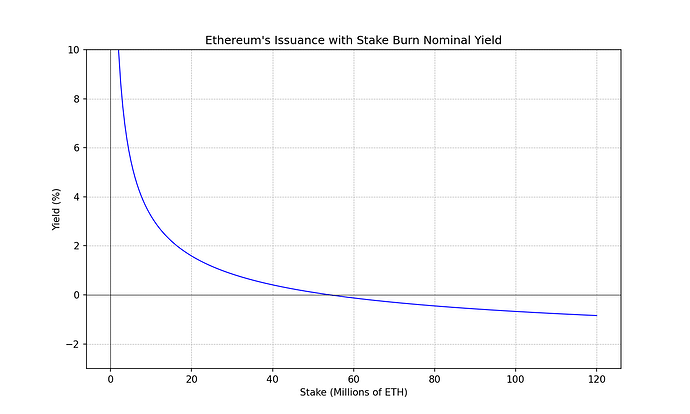
y_{s}(s) = 1 + \frac{2.6 \cdot 64}{\sqrt{s}} \quad \text{year}^{-1} y s ( s ) = 1 + 2.6 ⋅ 64 √ s年− 1
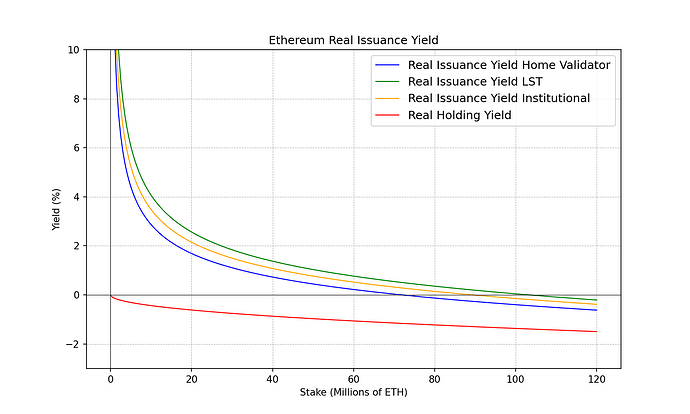
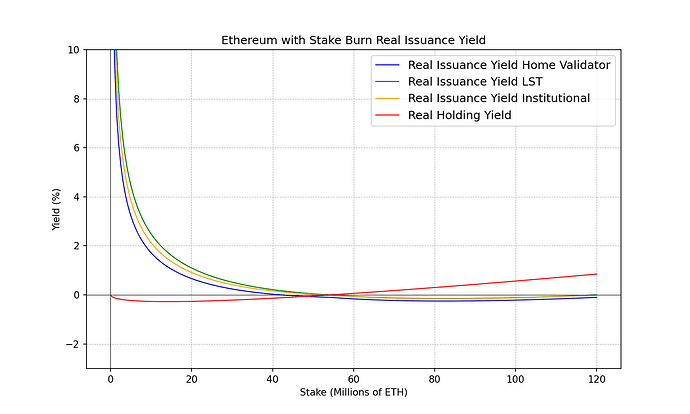
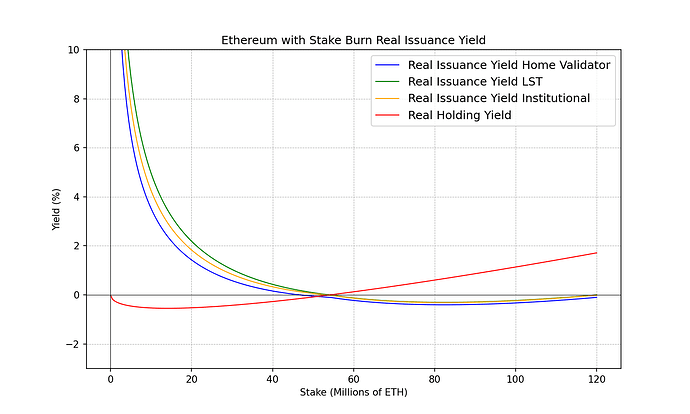
我们可以绘制上面介绍的 4 种不同类型的 ETH 利害关系人的实际收益率,以此视觉化由于经济规模和税收等外生因素而产生的可能的中心化力量。
我们可以做出以下观察,并从中得出一些结论。
观察结果
观察 0 :作为单独质押者、LST 持有者、ETH 持有者或任何其他选项参与的经济选择是根据观察到的实际收益率与每个风险(流动性、削减、运营、监管、智能合约… …)之间的差距做出的选项。通常较高的风险需要较高的保费。
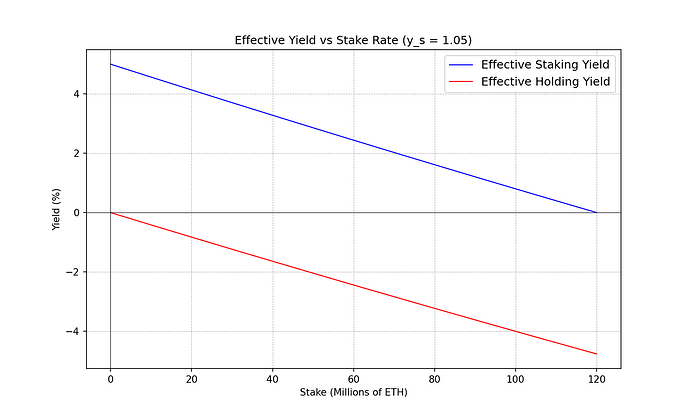
观察 1 :持有的实际收益率总是低于质押,至少对于上述成本假设而言是如此。但随著高股权率,差距缩小。
观察 2 :不同的质押者以不同的质押率跨越 0% 的实际收益率。大约 7,000 万个 ETH 质押的独立验证者开始赚取负实际收益率。大约 9,000 万枚 ETH 时,机构质押者开始赚取负实际收益率。大约 1 亿 LST 持有者开始赚取负实际收益率。
观察 3 :当每个质押者和每个 ETH 持有者都被稀释(实际收益率为负)时,质押对每个人来说都是净成本。
观察 4 :不同质押者的质押程度之间存在相当大的差距,实际收益率为 0%。
观察 5 :低名目报酬率对家庭质押者的影响大于对大型业者的影响。从上面的成本结构公式我们可以看出,只要名目报酬率为正,唯一能让实质报酬率为负的项就是c c 。这个字受规模经济的影响,小业者会遭受更大的c c 。
影响
观察 0和观察 1意味著,随著实际收益率之间的差距变得足够小,作为其中一些子集参与网络可能在经济上变得不合理。例如,考虑到营运风险、流动性风险、如果收益率溢价相对于持有而言足够小,单独质押可能在经济上是不合理的。在这种情况下,单独的质押者可能会成为持有者或转向其他形式的质押(例如 LST),其中溢价仍能满足风险。
与观察 2和观察 4一起意味著,随著质押率变得越来越高,链面临著变得更加中心化的风险,因为单独的质押者(这是最不相关的质押集合)必须继续质押,而这样做在经济上可能不合理。鉴于上述假设,即使在极端权益率(约 100%)下,LST 的实际收益率也总是比持有高出至少 1%,这可能意味著总是有动机持有 LST 而不是 ETH。此外,当单独的质押者实际收益率为负,而其他质押者没有这样做时,其他质押者正在缓慢而稳定地获得更大的权重。
从观察 3中我们知道,在非常高的权益率制度下,每个人都观察到负的实际收益率,这对每个人来说都是代价高昂的。每个人都观察到稀释。这笔钱将用于支付实际收益计算中包含的成本(税金、ISP、硬体、电力、劳动力…)。
观察 5表明,名目殖利率下降需要谨慎实施,当然不能孤立地实施,同时引入不相关激励措施。因为他们可能会严重惩罚本地单独的质押者。
建议
根据上述分析,我们可以提出殖利率曲线(发行曲线)应具有的一些建议性质。建立这些属性的想法是我们应该能够单独讨论它们并同意或不同意它们的可取性。一旦达成一致,它们就会限制我们应该考虑的功能集。至少,这将使发行变更的讨论更加结构化。
属性0 :虽然该属性已经满足目前的发行曲线,但值得明确说明。该协议应该激励一些最低限度的权益,以确保网路安全,并且攻击成本远大于这样做的潜在经济回报。这是透过定义一条殖利率曲线来实现的,该曲线随著权益总比例 ( s_n s n ) 的减少而提高名目报酬率。
属性 1 :殖利率曲线应包含不相关激励,以便激励质押者启动不相关节点并独立质押,而不是加入大规模业者。从协议的角度来看,透过大型质押操作质押另一个 ETH 获得的边际价值远小于透过不相关节点质押同一 ETH 所获得的边际价值。协议应该奖励不相关性,因为这使得网路能够实现协议期望从其验证器集获得的极端水平的审查阻力、活跃性/可用性和可信中立性。经济激励必须与预期结果保持一致,因此殖利率曲线必须包含不相关的激励。
性质 2 :发行曲线(或殖利率曲线)应具有这样一种机制:在足够高的股权率下,持有严格来说比股权更具有经济利益。这意味著,如果质押率够高,则持有的实际收益率大于质押的实际收益率。如上所述,实际收益率差距是确定加入一个子集或另一个子集的经济合理选择的决定性特征。如果在足够高的持股率下,持有的实际收益率可以大于质押的实际收益率,那么就会有持有而不是继续质押的经济动机。需要注意的是,到目前为止,我们还没有争论应该设定什么质押率。同意 99.9% 的权益率对协议来说是不健康的就足够了(这对每个人来说都是成本,LST 将取代 ETH 作为原始抵押品,等等…)。如果是这种情况,那么我们可以透过将持有实际收益率设定为高于该水准的质押收益率来防止这种结果。当权益率值低得多时,可能会发现不健康的水平。
属性 3 :为了防止中心化力量,不相关验证者与相关验证者交叉到负实际收益率的权益率应该很小,尽可能小。不相关(例如家庭质押者)和相关集合(例如大型运营商)的负实际收益率阈值之间的巨大差距创建了一个验证器集合可以变得越来越中心化的机制。为了使情况更清楚,如果不相关的验证者在质押30M ETH 时达到0 实际收益率,而持有由大型运营商(例如cbETH、wstETH)组成的LST,则在100M ETH 时达到0 实际收益率。质押范围在3000 万到1 亿之间的制度使得单独质押者往往会消失,要么很快(他们停止质押),要么缓慢(他们变得越来越稀释),无论哪种情况,结果都是更加中心化的验证者集。
属性 4 :殖利率曲线应相对快速地逐渐缩小,以进入负实际殖利率的状态。从属性 2和属性 3中,我们知道我们应该建立一种制度,使发行的实际收益率变为负值,但我们希望这种制度对于不同类型的质押者来说以大致相同的权益率发生,以防止中心化力量。观察 5意味著,如果名目殖利率下降的斜率很慢,则具有不同成本结构的质押者将以截然不同的质押率被挤出。因此,我们需要快速降低产量。
性质5 :发行殖利率曲线应该是连续的。使用不连续的殖利率曲线很诱人,但殖利率是调节网路总权益的主要动机。我们希望总权益s引起的变化是连续的,因此经济诱因应该是连续函数。
探索其他发行曲线
所需的属性可以非常简洁地总结:
- 殖利率曲线应该是连续的。
- 当权益率降至 0 时,殖利率曲线应该会上升。
- 随著权益率上升,殖利率曲线应趋于 0,并在高于所需权益率平衡点的某一点跨越 0。
- 殖利率曲线应该具有不相关的激励,这样,相对于相关的验证者来说,启动不相关的验证者会得到奖励和激励。
- 相关和不相关质押者的实际殖利率曲线应该变得相对接近的负值。
满足上述问题的一个非常简单的解决方案是在以太坊的发行收益率和不相关激励中引入一个负项。
随著股权的成长,负项的成长速度应该快于发行收益率,这样它最终会过度补偿发行,并使收益率在足够高的股权率下迅速变为负值。这个负面术语可以被认为是权益燃烧,并且应该在时段或纪元的基础上应用,这样它就不可避免了(感谢 A. Elowsson 的观察)。
其他贴文正在探讨不相关激励措施。我们将简单地将采用它们作为任何发行调整的一部分的建议保留在这里。延伸阅读: Wahrstatter 等人的反相关惩罚。
以太坊发行并销毁权益
以下是如何引入此类否定术语的范例。
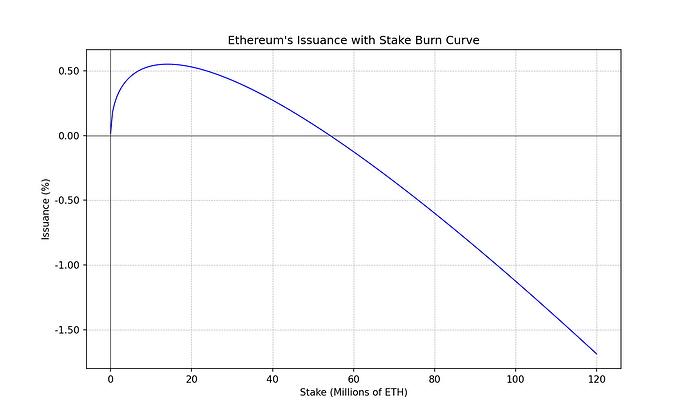
i(s) = 2.6 \cdot 64 \cdot \sqrt{s} - 2.6 \cdot \frac{s \ln s}{2048} \quad \text{ETH} \cdot \text{年份}^{-1} i ( s ) = 2.6 × 64 × √ s − 2.6 × s ln第2048章ETH ⋅年− 1
y_{s}(s) = 1 + \frac{2.6 \cdot 64}{\sqrt{s}} - \frac{2.6 \ln s}{2048} \quad \text{year}^{-1} y s ( s ) = 1 + 2.6 × 64 √ s − 2.6英寸第2048章年− 1
负股权销毁条款最终主导发行并可能使其变为负值。透过简单地调整常数前置因素,可以完全自由地决定该阈值发生的位置。在这种特殊情况下,我们选择的参数是以 2 的幂四舍五入的,因此负发行机制大致发生在 50% 的股权率左右。
这种负发行制度会为持有者带来正面的有效收益率,这为协议提供了限制权益率的经济诱因。因为持有 ETH 的实际收益最终会比质押更高。它还可以保护网路免于使其共识层过载,因为它为协议提供了一种机制,可以对发生在其之上的外生收益来源进行收费。如果优先费、MEV 或重新质押提供了额外的收益,将质押率推高到所需的限额之上,则协议将开始透过使发行量变为负数来向这些额外的收益来源收费。因此,将外生收益重新分配给 ETH 持有者。
为了更了解这种股权销毁对不同利害关系人的影响,我们可以绘制实际殖利率曲线。
我们可以看到负发行收益率制度的引入如何帮助实现了我们想要获得的大部分特性。特别是,我们可以注意到不同利害关系人达到 0 实际收益率的质押率已经压缩,并且彼此更加接近。我们可以理解,当权益率接近 50%(给定参数的选择)时,持有者开始观察到正的实际收益率,这会抑制额外的权益。持有实际收益率可能会变得相当大,因此即使是巨大的外生收益率来源也可以被克服。
鉴于我们还没有触及正发行期限,这会导致质押殖利率大幅下降。我们可以在保持相同的殖利率曲线形状的同时,微不足道地增加收益率。这里是相同的曲线,但产量更大:
i(s) = 2.6 \cdot 128 \cdot \sqrt{s} - 2.6 \cdot \frac{s \ln s}{1024} \quad \text{ETH} \cdot \text{年份}^{-1} i ( s ) = 2.6 × 128 × √ s − 2.6 × s ln 1024号ETH ⋅年− 1
y_{s}(s) = 1 + \frac{2.6 \cdot 128}{\sqrt{s}} - \frac{2.6 \ln s}{1024} \quad \text{year}^{-1} y s ( s ) = 1 + 2.6 × 128 √ s − 2.6英寸1024号年− 1
这表明在特定权益率下观察到的目标收益率是曲线形状讨论的单独考虑因素。因此,如果您因为当前权益率下的收益率而不喜欢这个特定范例。不用担心,这有一个简单的解决方法。
增加不相关激励措施
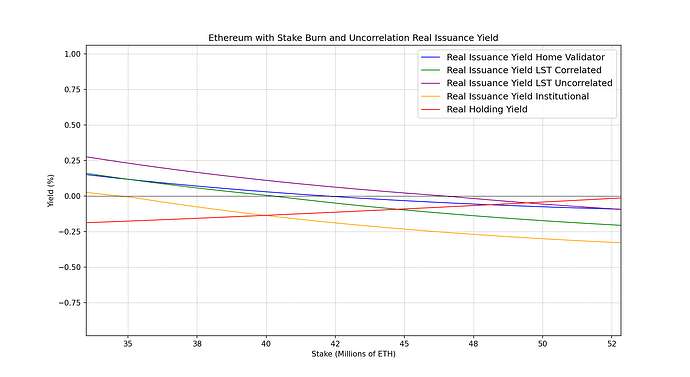
我们不会讨论如何引入不相关激励以及如何确定其规模的具体细节,但我们将说明引入相关性惩罚如何帮助将经济诱因与维护不相关验证器集的网路利益结合。
为此,我们将模拟以下利害关系人观察到的实际收益率会发生什么:
- 家庭验证器(非常不相关):透过相关性惩罚从名目殖利率中减去 -0.0%
- 通过去中心化协议的 LST 持有者(完全不相关):透过相关性惩罚从名目殖利率中减去 -0.2%
- 透过大型营运商质押的 LST 持有者(相当相关):透过相关性惩罚从名目殖利率中减去 -0.4%
- 大型机构营运商(高度相关):透过相关惩罚从名目殖利率中减去-0.6%
下图放大了实际收益率为负的区域:
重要提示:上述相关性惩罚值并非基于任何估计或研究。它们被任意选择,以表明在发行曲线中包含不相关激励可以用来抑制透过大型相关运营商进行质押。我们将正确激励的分析参考其他论文。
修复发行殖利率曲线
到目前为止,焦点一直集中在殖利率曲线(分别是发行曲线)的形状上,但很少有人讨论我们在不同权益利率下应该瞄准的具体殖利率。如上所述,透过简单地应用乘法因子,我们可以保持相同的曲线形状,但使收益率根据需要更高或更低。
在本节中,我们将提供一些启发式属性来解决此问题,并能够指定允许我们定义特定殖利率曲线的前置因素。
这些启发式属性是有方向性的。它们背后没有硬科学,只有一些软论点为这些选择提供合理的理由。
启发式 0 :名目发行殖利率在 50% 或更低的股权率下应变为负值。较高的质押率开始成为问题,高于该水平,大多数流通供应量都在质押。如果出现绝对多数错误,大多数 ETH 持有者可能会被激励打破共识规则。负收益制度可以被视为协议的一种保护机制,以防止此类情况发生,它设定了经济激励,使社会层与协议利益保持一致。
启发 1 :以 25% 的股权比例达到 3% 的目标收益率。当 PoS 发布时,不知道市场会考虑的预期质押收益率是多少。 5%就够了吗?还是3%?
现在我们有数据点,透过https://beaconcha.in衡量,目前的质押收益率为 3%(包括发行、MEV 和优先费用)。所以我们知道市场肯定对 3% 的 ETH 收益率有兴趣。 V. Buterin、J. Drake 等人也提出了一些温和的论点。 25%的股权率应该可以提供足够的安全性。
最后,目前的发行曲线恰好以 25% 的股权利率提供 3% 的收益率。因此,透过修复新曲线以满足 25% 的相同收益率,我们将相同的收益率(和发行量)锚定在目标利率。但任何额外数量的股份都会导致收益率和发行量的减少,使其在达到 50% 之前降至 0。
由于目前的持股率略高于 25%,因此提议的发行曲线变更将意味著发行量减少,但没有什么重大意义。但最重要的是,它避免了随著权益率的增加而不断增加的发行量。
与精心设计的不相关激励相结合,它可以帮助协议确保它不会为安全性付出过高的代价,权益率是自我限制的,并且验证器设定非常不相关。
最后的话
殖利率曲线或发行曲线的分析形式远不如我们想像的那么重要。花时间修改其具体的分析形式可能很诱人,但无论如何,它都可以用分段连续函数来同样定义。
其目的是提供经济激励,以获得协议所需的权益率(不太高,也不太低),并维护大量不相关的验证器集。
这篇文章旨在邀请大家将讨论引向上述属性,而不是迷失在细节中。如果我们确定属性,我们将充分限制解决方案空间,以便我们选择的几乎任何函数都可以完成这项工作。