在Vocdoni ，我们花了六年时间推进去中心化投票解决方案，专注于将 web2 应用程序与 web3 技术相结合。我们已成功为足球俱乐部、市议会、协会、政党、专业机构、受起诉的运动等组织执行了高风险投票。

直到今天，我们一直依赖于定制的权威证明第 1 层网络。
但我们认为，现在是时候过渡到基于零知识（zk）的基础设施，以实现完全去中心化并解决数字投票系统的主要挑战

在设计新协议提案的过程中，我们希望收到来自以太坊社区的反馈 。

通过借鉴我们的专业知识、MACI 和其他方面的想法。我们引入了一种新的通用投票协议，该协议解决了诸如无收据、选民隐私、审查透明度、通用审计以及消除对可信协调员的需求等关键问题。

该系统专为可扩展性和可访问性而设计，可实现适合大规模采用的高频低成本投票。我们利用 zkSNARK 和阈值同态加密 (ElGamal)，确保终端用户的端到端可验证性和匿名性。

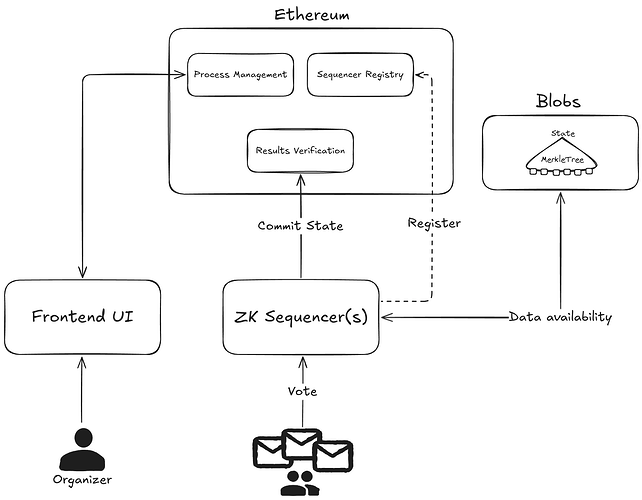
基于 zkSNARK 的去中心化状态机作为以太坊区块链上的专用第 2 层运行，提供抗审查性、完整性、无需信任的操作和透明的结果审查。通过智能合约协调的排序器之间的分布式密钥生成 (DKG) 允许在不依赖中央机构的情况下创建安全且去中心化的加密密钥。

大多数组件都已使用可访问的技术实现，并经过了概念验证测试，确认该协议实用且可立即部署。我们计划在 2025 年第一季度至第二季度启动测试网。

我们的实现在投票者端使用了 Circom 和 SnarkJS，支持从任何设备进行投票，包括智能手机和网络浏览器。对于排序器，我们使用 Gnark 和曲线 BLS12-377 和 BW6-761 来实现投票聚合中的原生递归。此设置生成最终的 BN254 证明，可在以太坊上进行验证。

我们专注于去中心化，设计了可在可访问机器（具有 64 GiB 内存的基于 CPU 的系统）上运行的排序器，这样参与就不需要专门的硬件。

演员

组织者设置并管理投票流程，定义投票选项、持续时间和选民登记（人口普查）等参数。

选民通过用户友好的界面与系统交互，使他们能够安全、私密地投票。选民生成 zkSNARK 来证明他们的加密投票符合投票规则，而不会透露他们的选择。

排序器是专门负责收集投票、验证投票有效性和更新共享状态的节点。它们参与分布式密钥生成 (DKG) 协议，以协作方式生成加密密钥，而无需任何一方控制私钥。

图像1383×1076 37.2 KB

特性

使用同态加密来维护隐私。投票使用椭圆曲线上的 ElGamal 密码系统进行加密，允许汇总加密投票而无需解密单个选票，从而保证选民选择的机密性。

完整性通过去中心化排序器网络的协作来保证，排序器维护一个共享状态，该状态由 Merkle 树表示，总结了投票过程的当前状态，包括累积投票和无效投票，以防止重复投票。每次用新投票更新状态时，排序器都会生成 zkSNARK 证明，证明状态转换的有效性。

通过防止选民向第三方证明他们如何投票，从而降低胁迫和贿选风险，可以实现无收据性。这是通过选票重新加密和选票覆盖机制实现的。当选民提交加密选票时，序列器会在将其存储在州内之前对其进行重新加密，这使得在计算上无法将原始密文和重新加密的密文联系起来。选民还可以覆盖他们的选票；如果选民投了一张新票，序列器会从计票中减去之前的加密选票并添加新的选票。序列器定期对随机选票进行重新加密可以隐藏覆盖发生的时间，通过使选票是被覆盖还是简单地重新随机化而无法区分，增强了无收据性。

端到端工作流程

1. 流程初始化：组织者定义投票参数（包括选项、持续时间和人口普查），并通过智能合约在以太坊区块链上注册新流程。
2. 分布式密钥生成 (DKG) ：序列器协作执行 DKG 协议以生成集体公钥加密密钥，而无需任何一方知道私钥。生成的公钥在链上发布，供选民在加密选票时使用。
3. 选民准备：选民从人口普查登记处检索公共加密密钥及其包含证明（Merkle 证明）。
4. 投票：选民选择他们的选择并使用公钥加密选票。生成 zkSNARK 证明以证明其加密投票的有效性，而无需透露他们的选择。加密的选票和证明将提交给排序器进行处理。
5. 投票收集和验证：序列器验证 zkSNARK 证明，以确保每次投票都符合协议规则。确认投票者符合投票资格且尚未投票，或适当处理投票覆盖。有效的加密投票以同态方式聚合，无需解密即可进行计票。序列器更新状态 Merkle 树以反映新投票和无效符。
6. 状态转换和证明提交：Sequencers 创建 zkProofs 来证明从前一个状态到新状态转换的有效性。新的根和相应的证明被提交给以太坊智能合约。合约验证数据并更新存储的状态根。
7. 数据可用性：重建状态所需的数据被发布到数据可用性层（以太坊数据块），确保可以验证和重建新状态。
8. 流程最终确定：在投票期结束时，流程在链上最终确定，不再接受进一步的投票。
9. 结果解密：排序器协作使用阈值解密协议解密汇总投票总数。解密结果在链上发布，提供不可改变且透明的结果。

门限同态加密

该系统采用椭圆曲线 bn254 上的 ElGamal 门限加密方案，该方案提供了安全聚合投票所必需的加性同态性质。

加密

投票者的选择表示为消息m \in \mathbb{Z}_q m ∈ Z q 。要加密投票：

1. 投票者将消息编码为椭圆曲线上的一个点： M = m G。M = m G。
2. 投票者选择一个随机标量k \in \mathbb{Z}_q^* k ∈ Z ∗ q 。
3. 密文计算如下： C = (C_1, C_2) = (k G, M + k H) 。C = ( C 1 , C 2 ) = ( k G , M + k H ) 。

同态加法

椭圆曲线上的 ElGamal 密码系统支持以点表示的消息的加法同态。给定两个密文(C_1^{(1)}, C_2^{(1)}) ( C ( 1 ) 1 , C ( 1 ) 2 )和(C_1^{(2)}, C_2^{(2)}) ( C ( 2 ) 1 , C ( 2 ) 2 ) ，它们的分量相加可得出：

• C_1^{(\text{sum})} = C_1^{(1)} + C_1^{(2)} C ( sum ) 1 = C ( 1 ) 1 + C ( 2 ) 1
• C_2^{(\text{sum})} = C_2^{(1)} + C_2^{(2)} C ( sum ) 2 = C ( 1 ) 2 + C ( 2 ) 2

聚合密文解密为消息的总和： M^{(\text{sum})} = M_1 + M_2 M ( sum ) = M 1 + M 2

阈值解密

投票期结束后，排序器协作解密聚合密文。每个排序器P_j P j计算部分解密份额：

1. 计算： D_j = s_j C_1。D j = s j C 1 。
2. 使用拉格朗日插值系数\lambda_j λ j组合部分解密：
   D = \sum_{j \in T} \lambda_j D_j = s C_1 D = ∑ j ∈ T λ j D j = s C 1
   其中T T是至少t个序列器的集合。
3. 通过计算可以恢复明文消息：
   M = C_2 - D = M + k H - sk G = M M = C 2 − D = M + k H − sk G = M
4. 最终结果m m是通过求解M = m G M = m G得到的，得出m m 。

分布式密钥生成 (DKG)

为了消除对可信机构的需求，选票加密所用的加密密钥由排序器通过分布式密钥生成协议协作生成，其过程如下：

1. 初始化：令G G为素数阶为q q的椭圆曲线群的生成器，预先定义阈值t t和序列器数量n n ，其中t \leq n t ≤ n 。
2. 秘密共享：每个序列器P_i P i随机选择一个度为t - 1 t − 1的秘密多项式f_i(x) f i ( x ) ，其中f_i(0) = a_{i,0} f i ( 0 ) = a i , 0 ，系数a_{i,j} a i , j从\mathbb{Z}_q Z q中均匀随机选择。
3. 承诺：每个序列器发布对其多项式系数的承诺： C_{i,j} = a_{i,j} G \quad \text{for} \quad j = 0, \ldots, t - 1. C i , j = a i , j G为了j = 0 ， … ， t − 1。
4. 份额分配：序列器P_i P i为每个其他序列器P_j P j计算份额： s_{i,j} = f_i(j), \quad \text{for} \quad j = 1, \ldots, n s i , j = f i ( j ) ，为了j = 1 , … , n
   这些共享使用 ECIES 的简化版本安全地传输到相应的序列器。
5. 验证：每个序列器P_j P j通过检查以下内容来验证收到的份额s_{i,j} s i , j ： s_{i,j} G \stackrel{?}{=} \sum_{k=0}^{t - 1} C_{i,k} \cdot j^k s i , j G ? = ∑ t − 1 k = 0 C i , k ⋅ j k
6. 私钥份额计算：每个序列器计算其私钥份额： s_j = \sum_{i=1}^n s_{i,j} \mod q s j = ∑ n i = 1 s i , j模式问
7. 公钥计算：集体公钥计算如下： H = \sum_{i=1}^n C_{i,0} = s G H = ∑ n i = 1 C i , 0 = s G ，其中s = \sum_{i=1}^n a_{i,0} \mod q s = ∑ n i = 1 a i , 0模式q是仅以排序器之间分布式形式知晓的聚合私钥。

投票

投票由以下列出的几个部分和机制组成。

进程标识符：投票进程的唯一标识符\text{ProcessId} ProcessId 。这可确保投票与特定投票事件正确关联，并防止跨进程干扰。

人口普查证明：Merkle 证明表明选民已被列入授权选民登记册（人口普查）。此证明允许排序器验证选民的资格，而无需透露整个选民名单，从而保护隐私和效率。

身份承诺：投票者使用加密哈希函数计算承诺： C = Hash(\text{Address} \parallel \text{ProcessId} \parallel s) C = H a s h ( Address ∥ ProcessId ∥ s ) ，其中H H是加密哈希函数， \text{Address} Address是投票者的唯一标识符（例如公钥或地址）， s s是只有投票者知道的秘密。

通过将秘密s s纳入承诺C C ，我们有效地将无效符与公开数据中选民身份的任何直接关联分离。这意味着，即使未来的量子计算进步会破坏 ElGamal 加密并泄露加密选票的内容，也没有切实可行的方法可以使用无效符将解密的选票链接回特定选民的地址。

无效符：为了防止重复投票和处理投票覆盖，投票者计算一个无效符： N = Hash(C \parallel s) N = H a s h ( C ∥ s ) 。无效符充当一次性令牌，唯一地代表投票者的参与，但不透露其身份。

通过避免在计算无效符时使用私钥或确定性签名，我们确保与硬件钱包和非确定性签名方案的兼容性。

选票：选票代表选民的选择，是一系列个人选择，必须遵守组织者定义的选票协议规则。这种灵活的方法使协议能够支持各种投票配置，包括范围投票、排名、二次投票等。

假设组织者想要实施具有以下参数的二次投票系统：

• 最大选择数：最多可以选择 5 个选项。
• 值范围：每个选择必须是非负整数。
• 总成本限制：选择的平方和不得超过 100 个信用的预算。
• 唯一值约束：允许重复值。

该协议将强制执行选票\mathbf{m} = (m_1, m_2, \ldots, m_5) m = ( m 1 , m 2 , … , m 5 ) ：

• 每个m_i \geq 0 m i ≥ 0 。
• \sum_{i=1}^5 m_i^2 \leq 100 ∑ 5 i = 1 m 2 i ≤ 100 .

加密选票：选民使用同态 ElGamal 加密方案加密选票，具体步骤如下：

• 选民的选择被编码成消息向量\mathbf{m} = (m_1, m_2, \ldots, m_n) m = ( m 1 , m 2 , … , m n ) ，其中每个m_i m i对应选票数组中的一个选择。
• 每个元素m_i m i被编码为椭圆曲线上的一个点： M_i = m_i G M i = m i G ，其中G G是曲线的生成器。
• 投票者选择一个随机标量k \in \mathbb{Z}_q^* k ∈ Z ∗ q ，其中q q是曲线的阶。
• 密文计算如下： C = (C_1, C_2) = \left( k G,\; \sum_{i=1}^n M_i + k H \right) C = ( C 1 , C 2 ) = ( k G , ∑n i = 1 M i + k H )​
  其中H H是从分布式密钥生成协议获得的公钥。

零知识证明（zkSNARK） ：选民生成一个 zkSNARK，在不透露选票内容的情况下证明：

• 正确的加密：加密选票根据加密方案正确形成。
• 协议合规性：投票者的选择遵守组织者定义的投票协议规则。
• 正确的无效符和承诺：使用投票者的秘密s和地址正确计算无效符和承诺。
• 秘密知识：投票者知道秘密s和加密中使用的随机标量k k 。

签名：投票者使用与其地址关联的私钥签署投票的必要部分。这将验证投票，并以可验证的方式将其与投票者的身份绑定。可以支持多种签名方案（ECDSA、EdDSA、RSA 等）。

状态转换

状态 Merkle 树是一种加密数据结构，可以高效安全地验证其所包含的数据。该树的结构用于在预定义的索引或地址中存储各种类型的信息：

• 过程参数：存储在静态索引中，包含必要信息，例如\text{ProcessId} ProcessId 、人口普查 Merkle 树的根（ \text{censusRoot} censusRoot ）、投票协议配置，以及通过 DKG 协议生成的公钥加密密钥H H 。
• 结果累加器：维护两个累加器来处理投票的加减：
  • 加法累加器（ C_{\text{add}} C add ）：存储已添加到计票中的同态聚合加密投票。
  • 减法累加器（ C_{\text{sub}} C sub ）：存储由于投票覆盖而减去的同态聚合加密投票。
• 无效符：存储以防止重复投票。每个无效符N N都与投票者的承诺相关联，并且对于特定投票流程而言对于该投票者是唯一的。
• 承诺：存储以跟踪选民参与情况并方便覆盖投票。

排序器负责处理新的投票并更新共享状态。每个状态转换涉及以下步骤：

1. 批量收集选票：排序器从投票者那里收集一批最多N N个新选票。批量投票可提高效率和可扩展性，使排序器能够同时处理多个选票。N N的值由平衡计算约束和网络吞吐量的系统参数决定。

2. 投票验证：对于批次中的每个投票，排序器执行：

   • zkSNARK 证明验证：确保每次投票提交的零知识证明有效，并且投票符合协议规则，包括正确的加密、遵守投票协议约束以及正确计算无效器和承诺。
   • 资格检查：通过检查提供的人口普查 Merkle 证明与州内存储的\text{censusRoot} censusRoot来验证选民的资格。
   • 防止双重投票：检查否决符N N是否已存在于该州。如果不存在，则该投票将被视为新投票。如果存在，则该投票被视为投票覆盖。

3. 处理投票覆盖：如果投票者使用相同的无效符N N提交新投票，则排序器：

   • 从减法累加器C_{\text{sub}} C sub中减去之前的加密投票。
   • 将新的加密投票添加到加法累加器C_{\text{add}} C add 中。
   • 取代州内新的加密选票。

4. 随机重新加密：为了增强无收据性并防止选票和选民之间的联系，序列器对现有的加密选票进行随机重新加密：

   • 选择该州加密选票的随机子集。
   • 使用新的随机标量，通过添加零加密来重新加密每个选定的选票。
   • 使用重新加密的版本更新该州的加密选票。

5. 投票的同态聚合：序列器使用 ElGamal 加密的同态性质来更新累加器：

6. 状态转换的生成 zkSNARK ：sequencer 生成一个 zkSNARK 证明，证明从前一个根\text{Root1} Root1到新根\text{Root2} Root2的状态转换的有效性。zkSNARK 证明验证了所有先前的约束和操作。

7. 链上提交：排序器提交：更新后的状态根\text{Root2} Root2 。状态转换有效性的证明。对包含投票和状态更新的数据 blob 的哈希承诺，确保数据可用性。

Vocdoni 代币 (VOC)

Vocdoni 推出了一种新代币 (VOC)，以协调参与者之间的激励机制并确保去中心化投票生态系统的可持续性。该代币具有多种基本功能：激励排序器、促进投票流程的支付并实现去中心化治理。

排序者必须质押代币作为抵押品才能参与网络，从而促进诚实行为和网络安全。他们根据对处理有效投票和维护网络完整性的贡献获得 VOC 代币奖励。

组织者使用代币支付创建和管理投票流程的费用。成本取决于多种因素，例如最大投票数（ \text{maxVotes} maxVotes ）、投票时长（ \text{processDuration} processDuration ）以及所需的安全级别，这与参与排序器的数量有关。

投票过程的总成本使用以下公式计算：

\text{总成本} = \text{基础成本} + \text{容量成本} + \text{持续时间成本} + \text{安全成本}总成本=基础成本+容量成本+持续时间成本+安全成本

成本组成部分：

• 基本成本： \text{baseCost} = \text{fixedCost} + \text{maxVotes} \cdot p baseCost = fixedCost + maxVotes ⋅ p ，其中\text{fixedCost} fixedCost是固定费用， p p是一个较小的线性因子。

• 容量成本： \text{capacityCost} = k_1 \left( \frac{\text{totalVotingProcesses}}{\text{totalSequencers} - \text{usedSequencers} + \epsilon} \cdot \text{maxVotes} \right)^a capacityCost = k 1 ( totalVotingProcesses totalSequencers − usedSequencers + ϵ ⋅ maxVotes ) a ，其中k_1 k 1是缩放因子， a a控制非线性， \epsilon ϵ是一个较小的数，以防止被零除。

• 持续时间成本： \text{durationCost} = k_2 \cdot \text{processDuration}^b durationCost = k 2 ⋅ processDuration b ，其中k_2 k 2作为缩放因子， b b根据持续时间控制缩放。

• 安全成本： \text{securityCost} = k_3 \cdot e^{c \left( \frac{\text{numSequencers}}{\text{totalSequencers}} \right)^d} securityCost = k 3 ⋅ e c ( numSequencers totalSequencers ) d ，其中k_3是比例因子， c c , d d控制与所用序列器数量相关的指数比例。

排序器根据处理的投票数和投票重写次数（包括无收据的重新加密）获得奖励。排序器i i的总奖励计算如下：

\text{sequencerReward}_i = R \left( \frac{\text{votes}_i}{\text{maxVotes}} \right) + W \left( \frac{\text{voteRewrites}_i}{\text{totalRewrites}} \right ) sequencerReward i = R ( votes imaxVotes ) + W ( voteRewrites i总重写数）

但受到以下限制：

\frac{\text{voteRewrites}_i}{\text{votes}_i} \leq T voteRewrites i投票i ≤ T且R > W R > W

确保排序器优先处理新投票而不是重写。这里， R R和W W分别是分配给处理投票和投票重写的奖励池的一部分， T T是限制每个投票重写次数的预定义常数。

未能履行义务的排序者可能会被削减抵押品，计算方法如下：

\text{SlashedAmount}_i = s \cdot \text{StakedCollateral}_i SlashedAmount i = s ⋅ StakedCollat eral i

其中s s是削减系数（ 0 \leq s \leq 1 0 ≤ s ≤ 1 ）。

资源

• 白皮书完整版： https://whitepaper.vocdoni.io

• 正在实施该协议的 MVP 版本的存储库列表：

  • 用于投票者的 Circom 电路GitHub - vocdoni/z-ircuits：Vocdoni Z snark 电路。
  • 序列器加密原语GitHub - vocdoni/gnark-crypto-primitives：用 Gnark 编写的一组自定义电路，支持 Vocdoni 上的匿名投票。
  • Circom 到 Gnark 解析器GitHub - vocdoni/circom2gnark:Circom 到 Gnark Groth16 解析器和递归示例
  • ElGamal 和 DKG 沙盒： GitHub - vocdoni/vocdoni-z-sandbox

• 联系方式：pau [at] vocdoni [dot] io

• Discord： https://chat.vocdoni.io