这篇文章的第二部分讨论了StableSwap不变量。

CryptoSwap

CryptoSwap不变量是一个核心数学公式,它定义了Curve交易池的"流动性曲线",专门设计用于高度波动的资产对(不像稳定币那样紧密挂钩)。它有助于池集中流动性在"内部"价格(通过内部预言机确定)周围,并在池失衡时自动调整。以下是关键要点:

结合两种不变量的优势:

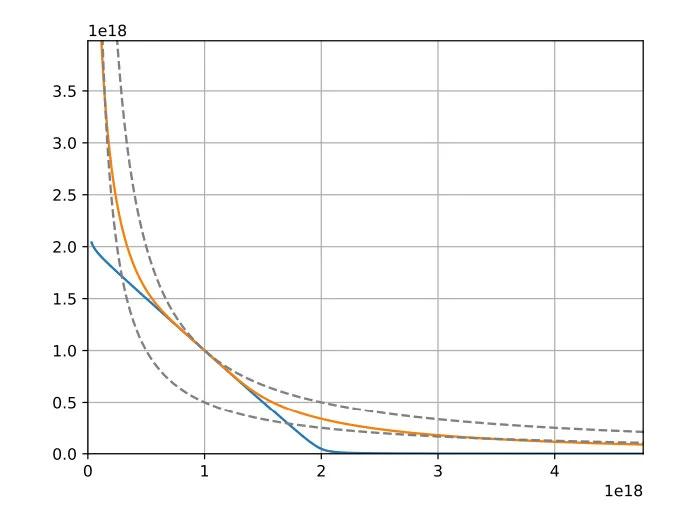
• 当池平衡(价值等价余额)时,CryptoSwap不变量的行为类似于StableSwap不变量,创造一个"平坦"区域(无滑点),实现近1:1的交换。

• 当池失衡时,不变量逐渐转向恒定乘积不变量行为(如Uniswap),导致滑点增加,并保护池免受过度价格偏离。

在第1部分中,StableSwap不变量描述在一般公式中:

CryptoSwap不变量由StableSwap不变量鼓励:

但是,K的定义略有不同:

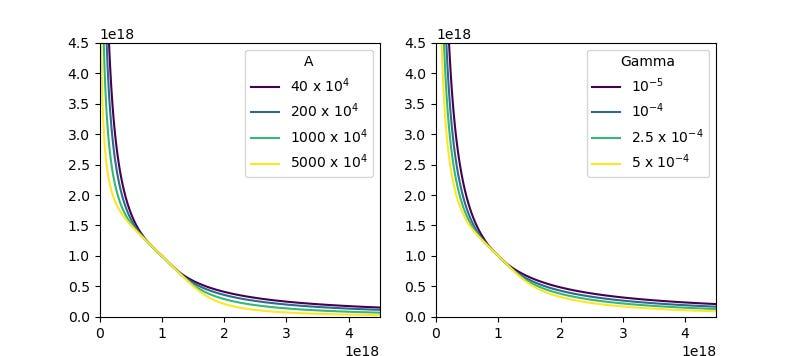
• A(放大系数):A参数类似于StableSwap不变量(Curve v1),控制曲线中心的平坦程度。这决定了流动性在预期汇率(即"价格尺度")周围的集中程度。

• Gamma:Gamma参数控制上图中两条恒定乘积曲线的分离程度(虚线)。当Gamma增加时,它会将"调整后的恒定乘积"曲线拉向左下角,使曲线的渐近线更靠近坐标轴,并扩大整体曲线形状。

初始化:

使用初始公式,我们可以将f(D_0)重写为只有2枚代币的情况:

使用牛顿法,初始值可以转换为:

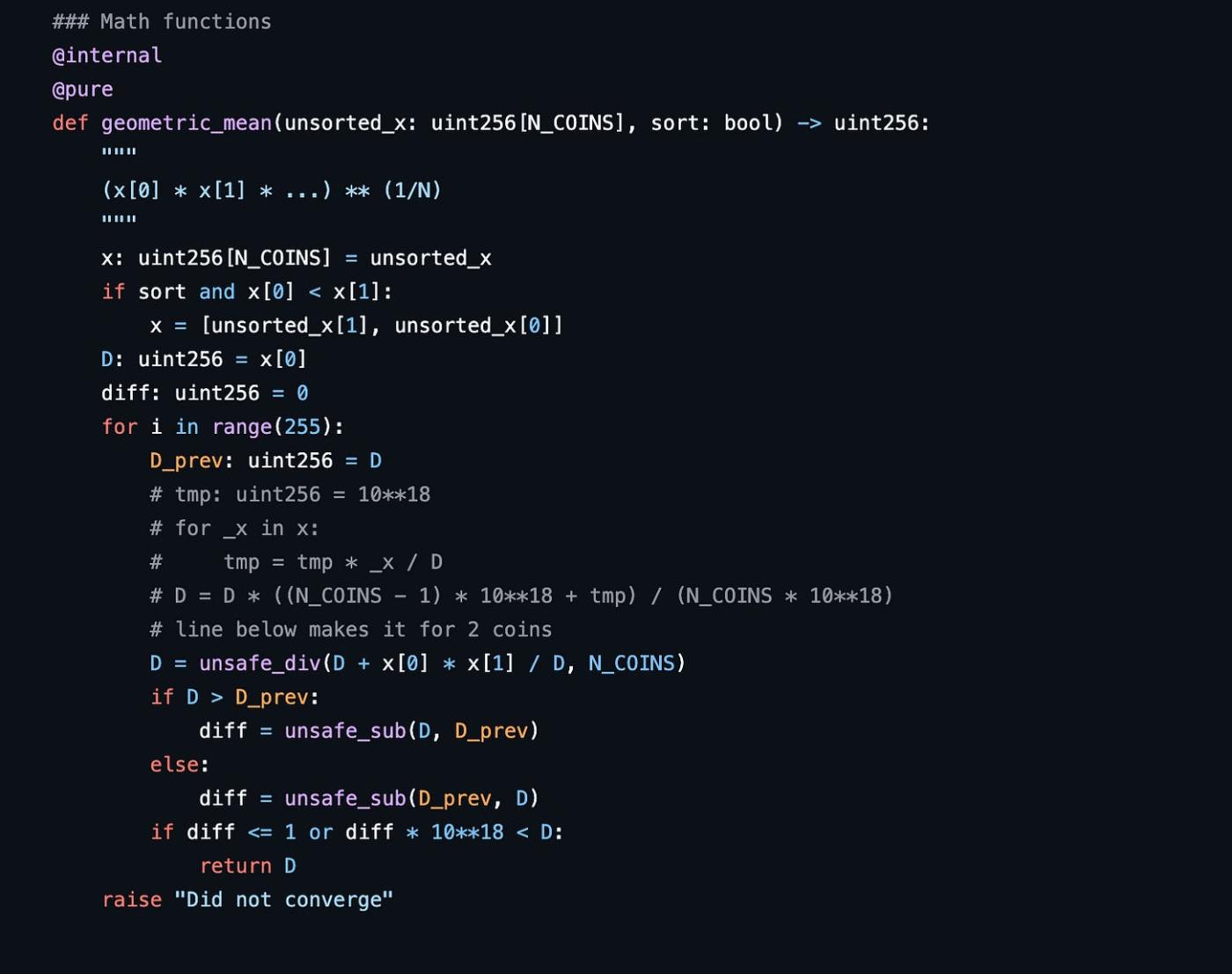
使用此公式,可以通过循环A次来计算D_0。在Viper代码中,A设置为255。

该代码计算当前和上一个D_0值之间的绝对差异。当差异非常小(diff ≤ 1)或当差异乘以10^18小于D_0时,它会停止迭代。满足其中一个条件后,该函数返回收敛的D_0值。

回到不变量,令S为x_i之和,P为x_i之积。对于2枚代币(N = 2),f(D)变为:

f(D)的导数为:

这可以转换为:

上述公式可以简化。首先,将所有项除以K,并展开括号内的所有内容。

现在S可以写为- S + 2S:

然后,提取包含S和D的组中的公共项。

使所有分母在括号内通用:

引入两个辅助变量mul1和mul2来简化函数中的变量:

现在,导数f'(D)可以简化为:

在Viper代码中,_g1k0变量被定义为:

回到代码中,

这段代码计算-f'(D)而不是f'(D)。这使牛顿步骤更加清晰。此外,f(D)被除以K:

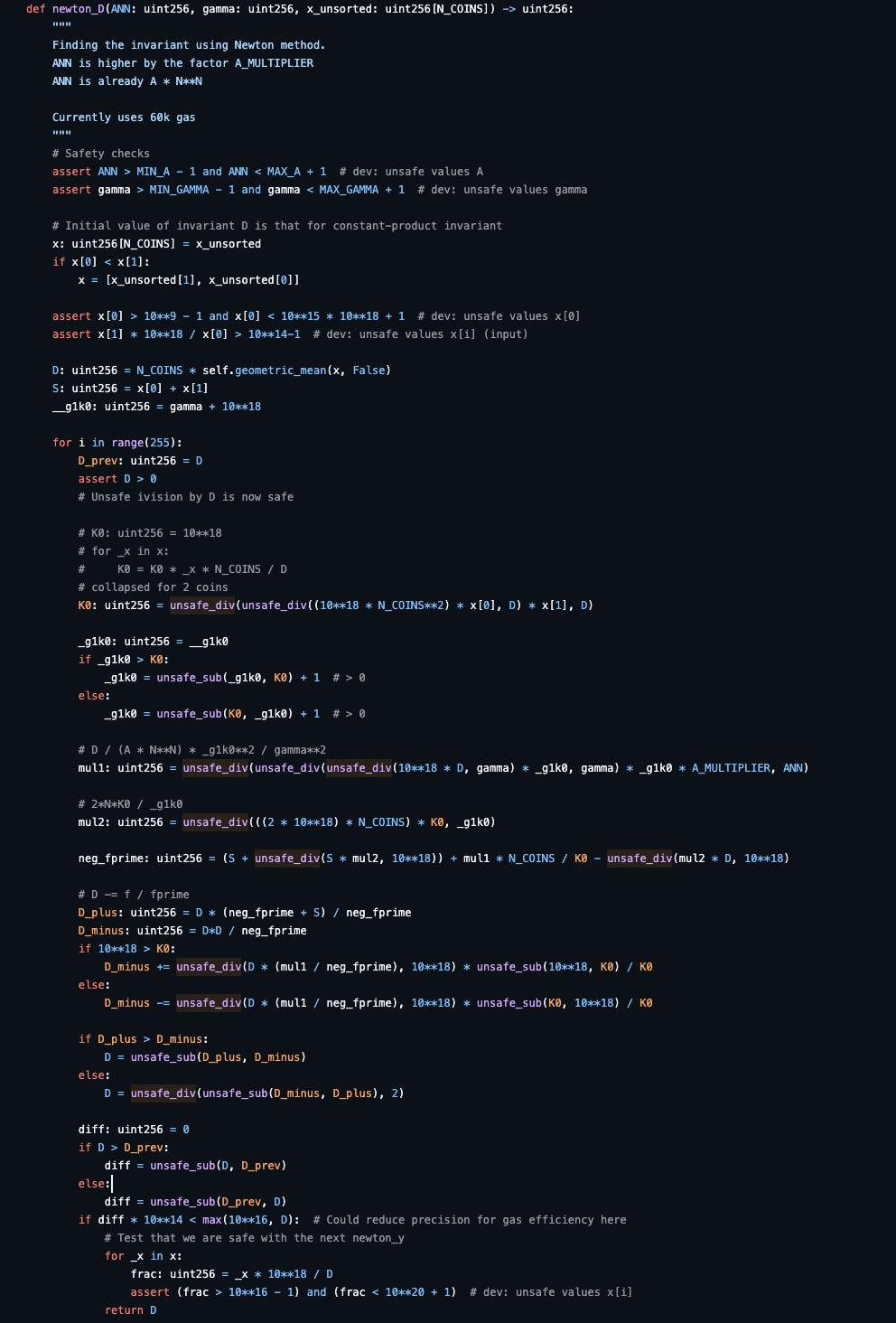
现在,D的完整牛顿法为:

该公式已分为两部分用于牛顿法:

最终的D将计算为上述两个方程的差。