基于格的签名聚合
这是 David Nevado、Dohoon Kim 和 Miha Stopar 的联合报告。
在以太坊的权益证明 (PoS) 中,BLS 签名用于将来自多个验证者的证明聚合成一个紧凑的签名。然而,BLS 并不具备量子安全性,在后量子时代,它将需要被取代。一个有前景的方向是基于格 (Lattice) 的聚合,例如最近发表的《使用 LaBRADOR 聚合 Falcon 签名》 (Aggregating Falcon Signatures with LaBRADOR) ,该论文探索了如何在保持小规模和快速验证的同时,高效地聚合后量子 Falcon 签名。
虽然 LaBRADOR 提供了一种很有前景的方法来聚合 Falcon 签名和紧凑证明(10,000 个签名约 74 KB),但也存在其他后量子替代方案。其中一种方法是使用 STARK,在零知识证明的情况下证明许多基于哈希的签名是有效的。这些方法通常会导致更大的证明大小( 10,000 个签名约 300 KB) ,但其优势在于更快的验证时间。
在本文的最后,我们将 LaBRADOR 方法与最近提出的基于哈希的签名聚合方法进行了比较。在后者方案中,签名使用 Poseidon2 实例化,而聚合则依赖于基于 Merkle 树的多项式承诺方案的 Keccak。聚合本身包括在 Plonk 风格的证明系统中对签名验证器进行算术运算。
LaBRADOR 是一个相对较新的协议,其实现支持仍然有限。虽然一些 Rust 实现正在涌现,但它们尚未成熟,因此目前主要使用原始的 C 语言参考代码。为了进行基准测试,我们使用了 Lazer 代码库中的agg_sig.py脚本,该脚本封装了LaBRADOR 的 C 语言实现。下文中,我们首先展示一些基准测试结果,然后解释 Lazer 方法与原始论文《使用 LaBRADOR 聚合 Falcon 签名》中描述的方法有何不同。
绩效结果
方法:
我们使用了LaBRADOR 的 fork 版本,其中包含一些修改,以支持更大的签名批次(超过 2,000 个签名)。这些修改是为了能够将模量增加到大约2^{48} 2 48 ,从而处理聚合过程中出现的较大中间值。
结果:
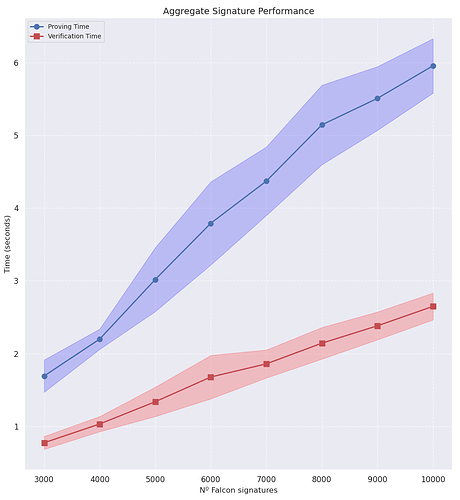
我们测量了 3,000 到 10,000 个 Falcon-512 签名批次聚合的验证时间。基准测试基于在11th Gen Intel(R) Core(TM) i5-11400H @ 2.70GHz处理器上进行单线程执行获得。
| # 签名 | 检验时间(秒) | 验证时间(秒) | 证明大小 |
|---|---|---|---|
| 3000 | 1.6921±0.2220 | 0.7739±0.0888 | 77.83 千字节 |
| 4000 | 2.1991±0.1403 | 1.0321±0.1044 | 69.82 千字节 |
| 5000 | 3.0182±0.4394 | 1.3380±0.2021 | 72.45 千字节 |
| 6000 | 3.7914±0.5716 | 1.6779±0.2989 | 72.11 千字节 |
| 7000 | 4.3709±0.4716 | 1.8586±0.1928 | 71.83 千字节 |
| 8000 | 5.1447±0.5469 | 2.1430±0.2175 | 74.02 千字节 |
| 9000 | 5.5085±0.4382 | 2.3821±0.1915 | 72.27 千字节 |
| 10000 | 5.9565±0.3750 | 2.6492±0.1848 | 74.07 千字节 |
注意:虽然图表中未显示,但此配置支持更大的签名批次。较小的批次(<2,000 个签名)可实现更佳性能,因为模量可以减小至2^{40} 2 40 ,从而缩短证明/验证时间并减少证明大小。
重点:
10k Falcon-512 签名可以与 LaBRADOR 聚合,从而产生:
- 74.07KB证明大小。
- 5.95秒证明生成。
- 2.65s证明验证。
从结果来看,验证时间是采用的最大障碍。我们对验证进行了分析,以提高其性能。
验证细目
Falcon 签名的聚合是使用打包证明和 LaBRADOR 库提供的 Dachshund 前端(有关 Dachshund 的简要描述,请参阅Lazer 论文)进行的。我们对 Dachshund 测试中的验证过程进行了性能分析,以找出瓶颈和潜在的优化机会。虽然我们尝试通过并行化来缩短原始验证时间,但这些努力并未成功。
分析
打包证明的验证需要1.2510秒,发生在composite_verify_simple中,该过程包含两个步骤:
- simple_reduce :从简单语句
st和证明p导出原始复合语句tst(1.1356 秒,约占总时间的 90%)。 - Composite_verify :根据
tst验证p(剩余 10%)。
鉴于其主导地位,我们专注于优化simple_reduce 。
simple_reduce分析
对于 48 位模数,常数LIFTS LIFTS = 3循环消耗了77% 的运行时间,但其顺序依赖性(由于 Fiat-Shamir 挑战)阻碍了并行化。
| 功能 | 时间(秒) | 总运行时间的百分比 |
|---|---|---|
init_statement() + betasq | 0.0000 | 0.00% |
reduce_simple_commit() | 0.0000 | 0.00% |
reduce_project() | 0.0451 | 3.97% |
init_constraint() | 0.0000 | 0.00% |
| LIFTS 循环 (3x) | 0.8800 | 77.50% |
free_constraint() + 清理 | 0.0016 | 0.14% |
simple_aggregate() | 0.1067 | 9.40% |
aggregate_sparsecnst() | 0.0969 | 8.53% |
reduce_amortize() | 0.0053 | 0.47% |
| 全部的 | 1.1356 | 100% |
在循环中,我们发现了几个可以优化的函数,特别是collaps_jlproj_raw() 。
LIFTS 循环细分(每次迭代)
| 功能 | 平均时间(秒) | 总运行时间的百分比 |
|---|---|---|
collaps_jlproj_raw() | 0.1166 | 10.27% |
polxvec_setzero() | 0.0178 | 1.57% |
simple_collaps() | 0.0537 | 4.73% |
reduce_lift_aggregate_zqcnst | 0.1053 | 9.27% |
| 总计(每次迭代) | 0.2934 | 25.84% |
| 总计(3 次迭代) | 0.8802 | 77.51% |
优化尝试
LaBRADOR 已针对 AVX-512 指令进行了大量优化,但仍保持单线程运行。我们探索了并行化,但遇到了一些挑战:
菲亚特-沙米尔依赖关系:
FS 挑战的推导不可避免地是连续的,这限制了并行化的机会。矩阵运算:
使用 OpenMP 并行化polxvec_jlproj_collapsmat(simple_reduce的 30%)会导致性能下降,可能是因为:- 错误共享(缓存行的线程争用)。
- 内存带宽饱和(AVX-512 已达到最大带宽)。
然而,需要进一步分析来找出根本原因。
比较:Lazer 和使用 LaBRADOR 聚合猎鹰信号
乍一看,使用 LaBRADOR 聚合猎鹰特征的技术似乎与 Lazer 的技术有很大不同,但事实并非如此。
让我们首先观察 Falcon 签名的聚合是如何工作的,然后深入研究两种方法之间的差异。
猎鹰签名
Falcon 签名由(s_1, s_2) ( s 1 , s 2 )组成,因此:
其中\mathbf{h} h是公钥的一部分, \mathbf{t} t是消息的哈希值。
我们正在使用除q q之外的其他模数的证明系统来证明\mathbf{s}_1 s 1和\mathbf{s}_2 s 2的知识,因此该等式被重写为:
对于某个多项式\mathbf{v} v 。
Falcon 签名的聚合
我们希望聚合N N Falcon 签名,这意味着证明:
其中i=1,..., N . i = 1 , ... , N .
注意, q q是 Falcon 方案中的模量,且方程需要在R_{q'} R q ′中成立,其中q' > q q ′ > q ,但环度d. d相同。为了证明等式在R. R上成立,方程中不能出现环绕模q' q ′ 。
论文《使用 LaBRADOR 聚合 Falcon 签名》使用LaBRADOR作为证明系统。在论文提交时,由于下文所述的问题,LaBRADOR 的使用受到了一些额外的限制。LaBRADOR 源代码及其 Dachshund 前端后来发布,事实上,Dachshund 前端直接解决了最初阻碍 LaBRADOR 正常使用的问题。
问题 1:规范检查
在 LaBRADOR 中,使用约翰逊-林登斯特劳斯投影进行范数检验是一种近似方法,并且一次性应用于所有见证向量。这种方法在 LaBRADOR 源代码中被称为“吉娃娃前端”。相比之下,“腊肠犬前端”则对每个见证向量分别执行范数检验。回想一下,在签名聚合的上下文中,我们有多个见证向量: \mathbf{s}_{i,1} s i , 1和\mathbf{s}_{i,2} s i , 2 。
由于 Dachshund 尚未发布,本文假设使用 Chihuahua 前端。该前端证明了整个见证(即所有见证向量的总和)的范数很小——这种方法适用于某些应用。
Johnson–Lindenstrauss 投影的思路是使用随机投影矩阵\Pi Π :对于见证\mathbf{s} s ,计算投影\Pi \mathbf{s} Π s (矩阵向量乘法),验证者直接计算投影向量的范数。有一个引理粗略地指出,如果投影很小,则原始向量也很小:如果|\Pi \mathbf{s}|_2 \leq \sqrt{30} b | Π s | 2 ≤ √ 30 b ,其中b为某个边界b ,则|\mathbf{s}|_2 \leq b | s | 2 ≤ b 。还必须满足\sqrt{\lambda} b \leq \frac{q}{C_1} √ λ b ≤ q C 1安全级别为\lambda λ和某个常数C_1 C 1 。这对聚合方案中使用的模量q q施加了约束——这也是本文使用更大模量q' > q q ′ > q而不是 Falcon 原始模量q q的原因之一。
然而,在签名聚合的情况下,需要证明每个见证向量(例如\mathbf{s}_{i,1} s i , 1和 $\mathbf{s}_{i,2}$)的较小性,而这正是 Dachshund 算法的设计初衷。由于 Dachshund 算法尚未面世,本文作者引入了额外的显式约束,以强制对各个见证向量施加范数界限。本文仍然使用了约翰逊-林登斯特劳斯投影,但目的不同:防止模回绕。下文我们将总结显式范数约束以及约翰逊-林登斯特劳斯投影在防止模回绕方面的应用。
个体见证向量范数约束
证明||\mathbf{s}_{i,1}||^2_2 + ||\mathbf{s}_{i,2}||^2_2 \leq \beta^2 | | s i , 1 | | 2 2 + | | s i , 2 | | 2 2 ≤ β 2等价于证明\beta^2 - ||\mathbf{s}_{i,1}||^2_2 - ||\mathbf{s}_{i,2}||^2_2 β 2 − | | s i , 1 | | 2 2 − | | s i , 2 | | 2 2为非负数。
拉格朗日四平方定理指出,任何非负整数都可以写成四个平方和。因此,我们可以找到四个整数\epsilon_{i,0}, \epsilon_{i,1}, \epsilon_{i,2}, \epsilon_{i,3} \in \mathbb{Z} ϵ i , 0 , ϵ i , 1 , ϵ i , 2 , ϵ i , 3 ∈ Z ,使得:
第i个签名的\epsilon_{i,j} ϵ i , j值作为多项式的系数添加到见证中
请注意,多项式\mathbf{a} = a_0 + a_1 X + ... + a_{d-1} X^{d-1}, a = a 0 + a 1 X + . . . + a d − 1 X d − 1 ,我们可以计算其范数为(利用||\mathbf{a}||^2 = ct(\langle \mathbf{a}, \sigma_{-1}(\mathbf{a}) \rangle) | | a | | 2 = c t ( ⟨ a , σ − 1 ( a ) ⟩ ) ,其中共轭自同构\sigma_{-1} σ − 1和X^d = -1 X d = − 1 ):
我们表示\mathbf{a}' = a_0 - a_{d-1} X - ... - a_1 X^{d-1}. a ′ = a 0 − a d − 1 X − . . . − a 1 X d − 1 .
现在我们可以将范数约束重写为 LaBRADOR 约束,如下所示:
但我们还需要检查新的见证元素是否已正确构建,以及见证元素的系数是否足够小,以至于它们不会环绕q'. q ′ 。
让我们观察如何表达一个约束,即多项式\mathbf{a} a的第 j j个系数是某个值,假设b: b :
对于每个\epsilon_i ϵ i ,我们需要准备约束以确保\epsilon_{i,4},..., \epsilon_{i, d-1} ϵ i , 4 , . . . , ϵ i , d − 1为零。
我们还需要确保\mathbf{s}'_{i,1} s ′ i , 1是从\mathbf{s}_{i,1} s i , 1正确构造的,例如:
对于\mathbf{s}_{i,2} s i , 2和\epsilon_i ϵ i也同样如此。
与基于四个平方和的方法相反,Dachshund 使用以 2 为底的分解向量,并将其与带有布尔系数的多项式相乘。性能上可能没有显著差异。
防止环绕
按照论文中的方法,需要确保以下两个方程不会出现环绕现象:
事实证明,第一个更具限制性,我们得到:
从第二个方程我们得到:
为了确保这一点,我们使用了约翰逊-林登斯特劳斯投影法。
问题二:重塑证人
在签名聚合方面,Chihuahua 前端的另一个限制是,由于需要计算大量所谓的垃圾多项式,因此在处理许多见证向量时效率低下。
证明器的运行时间——以及 LaBRADOR 收敛到基准情况的速度(即,压缩证明大小需要多少个递归步骤)——取决于两个关键参数:
- 多重性r r :见证向量的数量
- 秩n n :每个见证向量中的多项式数量
本文建议重塑见证人,以实现更加平衡的配置,目标是r = O(\sqrt{N}) r = O ( √ N )个秩为n = N的见证向量,其中N N是签名的数量。
最初,见证由r = 2N 个向量组成(添加精确范数约束后数量会更多),每个向量的秩为 n = 1。这是一个高度不平衡的配置。为了提高 LaBRADOR 递归压缩的效率,最好使r r和n n 的量级更接近。为了解决这个问题,该方案引入了一种填充策略:对见证进行重构,使得n \approx N n ≈ N且r \approx \sqrt{N} r ≈ √ N ,并根据需要用零填充新的见证向量。
然而,Dachshund 前端也解决了这个问题——Dachshund 旨在有效处理大量见证向量。
戒指选择
另一个方面是环的选择。虽然论文分析了多种方案,但最终采用了与 Lazer 相同的配置。多项式与几个小素数p_i p i相乘(使用 NTT),然后使用显式 CRT 模q q将结果合并。使用 16 位小素数p_i p i (介于2^{12} 2 12和2^{14} 2 14之间),完全拆分为\mathbb{Z}_r[X]/(X^{64} + 1) Z r [ X ] / ( X 64 + 1 ),可以实现高效的 Montgomery 算法(更多信息请参阅Greyhound 论文)。
概括
两种签名聚合方法(来自论文《使用 LaBRADOR 聚合 Falcon 签名》和 Lazer 方法)非常相似,因此我们相信我们的基准(基于 Lazer 代码)对两者都相关。
基准测试中,基于格的签名聚合方案最引人注目的特点是其证明大小,而其应用的最大障碍可能是验证时间。使用多线程技术或许可以提高验证性能,但这仍需要进一步研究。尽管如此,LaBRADOR 的作者们已经在对 LaBRADOR 协议及其 C 语言实现进行改进,预计这些改进将加快验证速度——尽管目前很难量化具体提升幅度。
虽然验证时间可能会随着未来的优化而改善,但它可能无法与基于哈希的方法相匹配(见下表),其中验证仅需几毫秒。
| 公制 | LaBRADOR + Falcon(10000 个签名,1 个线程) | 基于哈希(8192 个签名,4 个线程) |
|---|---|---|
| 证明大小 | 74.07 千字节 | 1.7 MB(优化后目标约为 128 KB) |
| 验证时间 | 5.95秒 | 5秒 |
| 验证时间 | 2.65秒 | 106毫秒 |
| PQ 安全 | 是(基于晶格) | 是(基于哈希:Poseidon2 签名,PCS 默克尔化中的 Keccak) |
| 并行化 | 有待探索 | 非常好——使用 4 个线程;几乎线性扩展到 4,但超过 4 时效率较低 |
总而言之,LaBRADOR 方案似乎非常适合 Falcon 签名聚合过程中出现的特定约束。为了缩短验证时间,探索类似于Dory 的委托技术可能是一个有前景的方向。这些协议降低了验证者的复杂性,在证明量较大但验证者资源受限的场景中尤其具有吸引力。