离开学术界后，我曾承诺自己不再写论文。但危急时刻，不得不采取非常措施！ 一个LVR问题困扰了我好几年。后来@MartinTassy解决了这个问题。 以下是一些历史和一些直觉 1/n

当@jason_of_cs、@ciamac、@Tim_Roughgarden 和 @alz_zyd_ 首次提出 LVR 的概念时，他们使用的是不含掉期费的模型。 这当然立即引发了一个问题：在包含掉期费的模型中，*净* LVR 会是多少？ 2/n moallemi.com/ciamac/papers/lvr...

我邀请了两位朋友（加州大学伯克利分校的 Dmitry Livdan 和高等经济大学的 Alex Boulatov）来证明以下结论。 流动性提供者的损失： * 波动率的三次方 * 与交换费成反比 * 与区块时间的平方成正比 然而，仍然存在两个问题…… 3/n

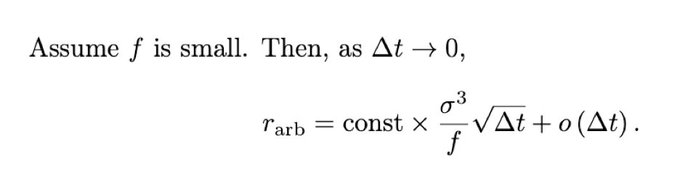
首先，我们的证明有点牵强（有点像福克-普朗克方程），至少我是这么理解的。 其次，我找不到使这个方程成立的确切常数。 所以我很自然地放弃了，转而发了一条推特。 4/n

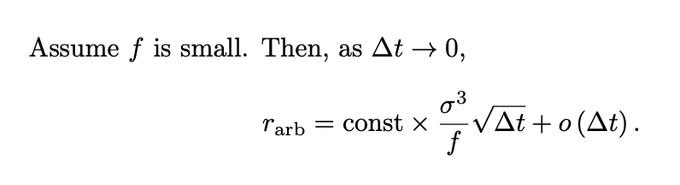
但随后@jason_of_cs、@ciamac 和 @Tim_Roughgarden 发表了他们的“带费用的 LVR”文章，其中除其他内容外，还包含： * 带费用模型中 LP 损失的精确公式 * 结果的完整证明 他们做到了…… 5/n moallemi.com/ciamac/papers/lvr...

一个优雅的假设：区块的到达遵循泊松过程。 这个假设适用于工作量证明链。但大多数权益证明链的出块时间都是固定的。 这让我思考：如果平均出块时间保持不变，那么…… 6/n

区块时间不确定性对套利者LP损失的影响？ 基本上，我们仍然需要确定那个常数！ 我锁定了。我不再给孩子们读书。取消了健身房会员资格。告诉朋友我的身体状况不好。问了我认识的每一位统计学教授…… 7/n

然后我想起@MartinTassy和@_Dave__White_之前研究过类似的问题，但使用的工具略有不同。 （我尽可能在连续时间上进行计算，然后弄清楚在邻近的离散模型中会发生什么，但他们的方向相反。） 8/n

所以我联系了马丁。 通过比较固定时间和泊松块到达模型，可以清楚地看出一点。LP 的损失是以下因素的乘积： ARB掉期的概率 * 每次套利掉ARB的损失。 事实证明，套利掉ARB的*概率*... 9/n

只是*平均*出块时间的函数。区块是以固定间隔还是按照泊松模型到达并不重要。 但是，当出块时间固定时，每次套利掉期的损失较小。为什么？ 损失会随着 CEX 价格的上涨而增加…… 10/n

在区块间隔时间内，超过 DEX 的买卖价差。 要超过价差，CEX 价格首先需要达到价差的边界，然后利用到下一个区块的剩余时间超过价差。 在泊松模型中，如果平均出块时间为 12 秒…… 11/n

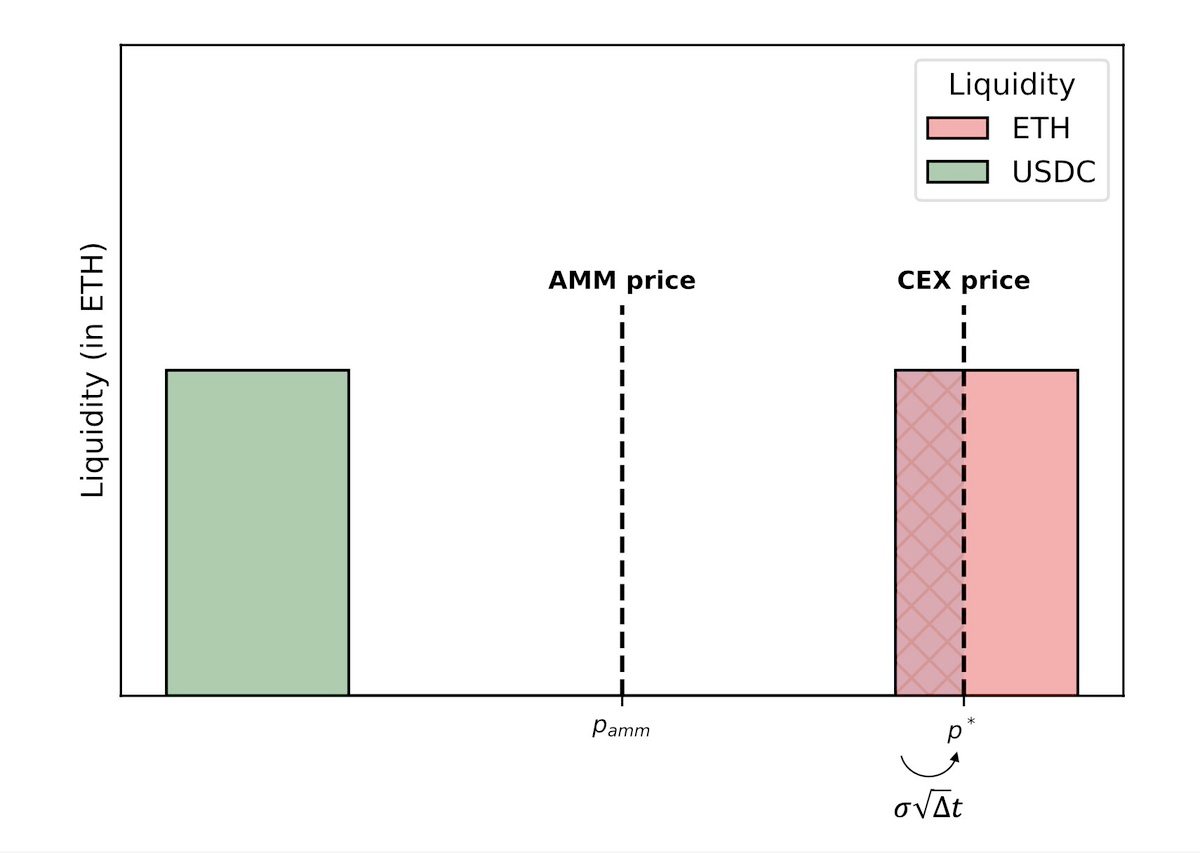
价格在前一个区块生成后 2 秒达到边界，那么平均仍然需要 12 秒才能达到超调量。但如果区块时间固定，则只需要 10 秒。 在下面的论文中，Martin 和我给出了固定区块时间下损失的精确表达式。 12/n

事实证明，我们要寻找的常数包括在 1/2 处求值的黎曼 zeta 函数。 我觉得我们已经接近将AMM研究与黎曼假设联系起来了，考虑到一切都始于 xy=k，这非常令人印象深刻！ http:/arxiv.org/pdf/2505.05113