从一维和二维角度重新审视安全DAS

作者： Benedikt （ @b-wagn ）、 Francesco （ @fradamt ）

所有代码均可在笔记本中找到。

一、引言

随着Fusaka 升级，以太坊将引入一种名为PeerDAS的数据可用性采样 (DAS)机制。底层数据单元blob使用 Reed-Solomon 码进行水平扩展，并排列为矩阵的行。样本则作为矩阵的列。

图片2752×736 133 KB

列也是网络上的传输单位，目前无法交换小于列的单位。因此，PeerDAS 的初始版本缺少两个功能：

• 部分重建：仅通过重建和重新播种部分数据（例如，仅一行（或几行）而不是整个矩阵）即可为重建做出贡献。
• 完全兼容内存池：交易附带 blob/行，通常会提前分发到内存池中。然而，任何单个 blob 的缺失都会阻止节点构建列，从而导致所有其他内存池 blob 失效。

为了解决这些限制，单元级消息传递已被强烈考虑作为该协议下一轮迭代的候选方案（例如，参见此处）。由于这也是二维 DAS 构建的关键组成部分，这引发了一个问题：我们是否应该：

• 通过单元级消息传递增强 1D PeerDAS，或
• 过渡到 2D 构造。

或者至少，这种转变是否会是后续的迭代。在本文中，我们将比较这两种方法的效率，假设它们都旨在提供相同级别的安全性，同时最大限度地减少带宽消耗。

免责声明：我们将完全忽略“加密层”的安全性，即所使用的 KZG 承诺的安全属性。该层已在此处和此处进行了广泛的研究。我们的重点是与采样过程相关的统计安全属性，并将加密层视为理想化。

背景：数据可用性采样

让我们首先抽象地回顾一下数据可用性采样（DAS）背后的核心思想。

在 DAS 中，提议者持有一段数据，并希望将其分发到整个网络。客户端（可能是全节点或验证者）的目标是验证该数据确实可用，而无需完整下载。

为了实现此目的，提议者使用纠删码扩展数据。然后，每个客户端尝试下载结果码字的k k 个随机符号，并根据所有客户端都会下载的简洁加密承诺进行检查。在 DAS 中，这些符号也称为样本或查询。只有当所有k k 个查询都成功验证后，客户端才会接受数据（例如，在其分叉选择中包含相应的区块）。

DAS 安全性（针对潜在的恶意提议者）背后的高级直觉是：

• 加密承诺保证提议者承诺使用有效的代码字（请参阅此处的代码绑定概念）；
• 如果有足够多的客户端接受，那么由于擦除码的属性，他们的集体查询允许重建完整的数据。

这篇文章主要讨论第二点：重构究竟是如何实现的？多少个客户端才够用？参数k又该如何设置？

我们首先解决第一个问题，解释一下“部分重建”的含义。然后，我们将重点转向安全性。

背景：部分重建

DAS 的核心问题之一是：谁能重建数据？何时重建？假设我们有一个无所不能的“超级节点”，它能够从网络下载足够多的样本，重建通过纠删码编码的全部数据。在这种情况下，即使只有少数代码符号缺失（可能是被恶意提议者隐瞒的），这个超级节点也可以简单地重新计算缺失的部分，并将其重新引入网络（即重新播种）。最终，这些符号会被传播，所有客户端都会接受。

这种设置引发了对如此强大的超级节点的依赖担忧，这可能是一个中心化因素。事实上，即使我们使用具有最小重建阈值的纠删码（例如Reed-Solomon等所谓的MDS码） ，超级节点也需要下载与完整原始数据一样多的样本才能重建数据。

这时，部分重建的概念就应运而生了。如果某个代码能够使用比完全重建所需的样本少得多的样本量来恢复数据中较小的局部部分，我们就称其支持部分重建。无需超级节点收集几乎所有数据片段，多个较小的节点就可以独立地重建部分数据。通过这种方式，部分重建可以将重建任务分散到众多参与者身上，从而减少对中心化超级节点的依赖。

除了通过减少对更强大节点的依赖来增强网络的稳健性之外，分散重建的 CPU 负载和重新播种重建数据的带宽负载也可以被视为性能提升。目前，重建不太可能帮助数据在关键路径上传播，这或许是采用纠删码的另一个好处，因为重建一个包含所有证明的 blob大约需要 100 毫秒。通过将此负载分散到多个节点，每个节点只负责一个或几个 blob，纠删码的作用远不止于安全保障。

背景：子集健全性

在本文中，我们将比较不同编码方案（一维和二维）的效率，假设它们都能达到相同的安全级别。为了使比较更有意义，我们首先需要清楚地理解在 DAS 环境中“安全”的含义。

我们考虑的安全概念被称为子集健全性，并考虑了自适应对手。该概念在《DAS基础》论文中作为定义2正式引入，它也是PeerDAS安全原理的基础。

直观地讲，子集健全性模型模拟了一个强大的对手，他会观察大量n个客户端/节点的查询。然后，对手可以自适应地决定显示哪些符号、隐藏哪些符号，从而有效地构建每个节点看到的视图。对手还会选择一小部分节点（例如， \epsilon n \leq n ϵ n ≤ n ，其中\epsilon > 0 ϵ > 0 ），并试图欺骗这些节点，使其相信数据完全可用。值得注意的是，这种选择可能取决于节点发出的查询。然后，我们考虑对手赢得这场游戏的概率p p ，即

• \epsilon n ϵ n个节点全部接受，并且
• 数据并不完全可用；也就是说：人们无法从查询中重建数据。

为了达到我们的目的，我们希望p p最多为2^{-30} 2 − 30 （对于任何对手）。下面，我们将根据n n 、 \epsilon ϵ和编码方案设置每个节点的查询次数k k ，以保证p \leq 2^{-30} p ≤ 2 − 30 。

\epsilon ϵ的影响和选择：
上面描述的安全概念由\epsilon \in (0, 1] ϵ ∈ ( 0 , 1 ]参数化，它模拟了对手试图欺骗的节点比例。从正式定义和简单的密码学简化来看，给定\epsilon ϵ （具有固定的n n ）的子集健全性意味着任何更大的\epsilon' \geq \epsilon ϵ ′ ≥ ϵ的子集健全性。换句话说：如果对手无法欺骗\epsilon ϵ比例的节点，那么它肯定无法欺骗更大比例的\epsilon' ϵ ′ 。

但这与整体共识协议有何关系？假设我们知道攻击者最多只能欺骗ε ϵ比例的节点。每个被欺骗的节点实际上在共识过程中充当一个额外的恶意节点。因此，当使用数据可用性抽样时，攻击者最多可以获得额外 ε ϵ比例的明显恶意节点。

例如，如果没有 DAS 的共识可以容忍最多<{1}/{3} < 1 / 3 个恶意节点，那么有了 DAS，系统现在只能容忍最多<{1}/{3} - \epsilon < 1 / 3 − ϵ 个恶意节点。

因此，在实际操作中，我们必须选择较小的\epsilon ϵ ，比如\epsilon = 1\% ϵ = 1 % ，以确保对手的影响可以忽略不计。

二、PeerDAS——一维构造

在本节中，我们将解释PeerDAS的工作原理，它将包含在Fusaka升级中。我们还将解释单元级消息传递如何实现部分重建。

工作原理

我们描述了如何编码数据以及客户端如何进行查询，而忽略了与“加密层”相关的所有内容，例如承诺和开口。

一个blob是由m个单元组成的集合，每个单元包含f个字段元素。在 PeerDAS 当前的参数设置中，每个单元包含f = 64个字段元素，每个 blob 包含m = 64个单元。为了考虑不同的单元大小，我们令fm = 4096为常数（即数据大小固定） ，并在f ∈ { 64,32,16,8 }之间变化，即m = 4096 / f 。

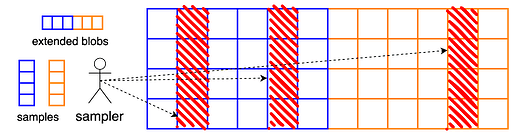
要对单个 blob 进行编码，需要使用速率为1/2 1/2的Reed -Solomon 码对其进行扩展，从而得到2m 2 m个单元，或者等效地得到2fm = 8192 2 f m = 8192 个字段元素。在 PeerDAS 中，我们将此编码过程分别应用于b b 个blob，并将扩展后的 blob 视为b \times 2m b × 2 m个单元矩阵中的行。

客户端现在查询该矩阵的整列，也就是说，它们尝试一次性下载b个单元。这意味着“符号”或我们的纠删码是扩展 blob 矩阵的列。从这些列中的任意m个列，都可以重建整个矩阵，从而重建数据。

支持采样功能的具体网络基础设施是列的 GossipSub 主题，即只有对特定样本（= 列）感兴趣的节点参与的子网络。

部分重建

正如预期的那样，当前的PeerDAS设计不支持部分重建。然而，即使是这样的一维编码，原则上也可以支持此功能，当它独立应用于多个blob时，就像在PeerDAS中一样。事实上，通过使用小于列的垂直单位（例如单元格），当然可以仅重建完整矩阵的部分内容，例如单独的行或行组。这带来了两个挑战：

1. 部分重新播种：当一个节点重建单行时，它不会重建任何完整的样本（列），但它仍然需要能够将重建的数据贡献回网络。
2. 获取足够的单元进行重建：当仅对列进行采样时，重建能力要么全部，要么全部不重建，也就是说，一个节点要么获得足够的列来重建整个矩阵，要么无法重建矩阵的任何部分。换句话说，只有超节点才能参与重建。我们希望节点能够做到这一点，同时仍然只下载整个数据的一小部分。

有一些众所周知的方法可以解决这些问题，这些方法可以让我们进行部分重建：

1. 单元级消息传递：使节点能够交换单元而不是整列，以便重建行的节点可以逐个单元地重新播种，至少在它们参与的列主题中是这样。
2. 行主题：有些节点也尝试通过参与行主题下载部分行，并配备单元级消息传递功能。至关重要的是，这并非采样，获取多少行并不涉及安全隐患，因此即使只参与一个行主题也足够了。事实上，在一维结构中，对行进行采样毫无意义，因为不存在垂直冗余。行主题的目的仅仅是使列主题中的单元能够流入其中并实现行向重构，而无需任何超节点。重构后的单元随后可以从行主题流入所有列主题，同样无需任何单个节点参与所有列主题。

注意：缺乏垂直冗余意味着我们需要每个行主题都能成功执行其重建任务。即使只有一个行主题失败（例如，由于仅限于该主题的网络级攻击），整个重建也无法完成。

样本数量

现在让我们确定PeerDAS每个客户端的样本数量k 。如上所述，我们希望选择k ，使得攻击者破坏子集健全性的概率p最多为2^{-30} 2 − 30 。

PeerDAS 的安全性已在这里和这里进行了广泛的分析。后者的工作建立在这里的安全框架之上，并且可以通过结合引理 1 和引理 3得出子集健全性的具体界限。最终，所有这些得出了相同的子集健全性界限，即：

p \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot (\frac{m-1}{2m})^{kn\epsilon} \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot 2^{-kn\epsilon}. p ≤ ( n n ϵ ) ⋅ ( 2米米− 1​ ) ⋅ （米− 1 2米) k n ϵ ≤ ( n n ϵ ) ⋅ ( 2米米− 1​ ) ⋅ 2 − kn ϵ 。​

直观地讲，第一个二项式表示对手自由且自适应地挑选n\epsilon n ϵ个节点来欺骗的能力，第二个二项式表示对手选择m-1 m − 1 个符号来提供给这些节点，最后一个项是所有样本最终都出现在编码的可用部分中的概率。

如果我们希望p \leq 2^{-30} p ≤ 2 − 30且n,m,\epsilon n , m , ϵ已知，我们需要设定

k \geq \frac{1}{n\epsilon} \left( \log_2 \binom{n}{n\epsilon} + \log_2 \binom{2m}{m-1} + 30 \ right ) k≥1nϵ （日志2 ( n n ϵ ） + log 2 （ 2米− 1​ ） + 30 ） 。

以下是计算k k的代码：

 from math import comb, log2, ceil # used later from tabulate import tabulate # used later import numpy as np # used later import matplotlib.pyplot as plt # used later def min_samples_per_node ( n: int , m: int , r: int = 2 , eps: float = 0.01 ): """Finds the smallest integer k such that k samples per nodeachieve security of 30 bits for the 1D construction.Inputs:n: total number of nodesm: number of symbols in original datar: inverse coding rate (total symbols = r*m), default=2eps: fraction of nodes to be fooled (0 < eps <= 1), default=0.01Returns:Smallest integer k satisfying the bound""" neps = int (n * eps)binom_n = comb(n, neps)binom_m = comb(m*r, m- 1 )log2_binom = log2(binom_n) + log2(binom_m)k = -(log2_binom + 30 )/(n*eps*log2( 1 /r)) return ceil(k)

列也是网络上的传输单位，目前无法交换小于列的单位。因此，PeerDAS 的初始版本缺少两个功能：

• 部分重建：仅通过重建和重新播种部分数据（例如，仅一行（或几行）而不是整个矩阵）即可为重建做出贡献。
• 完全兼容内存池：交易附带 blob/行，通常会提前分发到内存池中。然而，任何单个 blob 的缺失都会阻止节点构建列，从而导致所有其他内存池 blob 失效。

为了解决这些限制，单元级消息传递已被强烈考虑作为该协议下一轮迭代的候选方案（例如，参见此处）。由于这也是二维 DAS 构建的关键组成部分，这引发了一个问题：我们是否应该：

• 通过单元级消息传递增强 1D PeerDAS，或
• 过渡到 2D 构造。

或者至少，这种转变是否会是后续的迭代。在本文中，我们将比较这两种方法的效率，假设它们都旨在提供相同级别的安全性，同时最大限度地减少带宽消耗。

免责声明：我们将完全忽略“加密层”的安全性，即所使用的 KZG 承诺的安全属性。该层已在此处和此处进行了广泛的研究。我们的重点是与采样过程相关的统计安全属性，并将加密层视为理想化。

背景：数据可用性采样

让我们首先抽象地回顾一下数据可用性采样（DAS）背后的核心思想。

在 DAS 中，提议者持有一段数据，并希望将其分发到整个网络。客户端（可能是全节点或验证者）的目标是验证该数据确实可用，而无需完整下载。

为了实现此目的，提议者使用纠删码扩展数据。然后，每个客户端尝试下载结果码字的k k 个随机符号，并根据所有客户端都会下载的简洁加密承诺进行检查。在 DAS 中，这些符号也称为样本或查询。只有当所有k k 个查询都成功验证后，客户端才会接受数据（例如，在其分叉选择中包含相应的区块）。

DAS 安全性（针对潜在的恶意提议者）背后的高级直觉是：

• 加密承诺保证提议者承诺使用有效的代码字（请参阅此处的代码绑定概念）；
• 如果有足够多的客户端接受，那么由于擦除码的属性，他们的集体查询允许重建完整的数据。

这篇文章主要讨论第二点：重构究竟是如何实现的？多少个客户端才够用？参数k又该如何设置？

我们首先解决第一个问题，解释一下“部分重建”的含义。然后，我们将重点转向安全性。

背景：部分重建

DAS 的核心问题之一是：谁能重建数据？何时重建？假设我们有一个无所不能的“超级节点”，它能够从网络下载足够多的样本，重建通过纠删码编码的全部数据。在这种情况下，即使只有少数代码符号缺失（可能是被恶意提议者隐瞒的），这个超级节点也可以简单地重新计算缺失的部分，并将其重新引入网络（即重新播种）。最终，这些符号会被传播，所有客户端都会接受。

这种设置引发了对如此强大的超级节点的依赖担忧，这可能是一个中心化因素。事实上，即使我们使用具有最小重建阈值的纠删码（例如Reed-Solomon等所谓的MDS码） ，超级节点也需要下载与完整原始数据一样多的样本才能重建数据。

这时，部分重建的概念就应运而生了。如果某个代码能够使用比完全重建所需的样本少得多的样本量来恢复数据中较小的局部部分，我们就称其支持部分重建。无需超级节点收集几乎所有数据片段，多个较小的节点就可以独立地重建部分数据。通过这种方式，部分重建可以将重建任务分散到众多参与者身上，从而减少对中心化超级节点的依赖。

除了通过减少对更强大节点的依赖来增强网络的稳健性之外，分散重建的 CPU 负载和重新播种重建数据的带宽负载也可以被视为性能提升。目前，重建不太可能帮助数据在关键路径上传播，这或许是采用纠删码的另一个好处，因为重建一个包含所有证明的 blob大约需要 100 毫秒。通过将此负载分散到多个节点，每个节点只负责一个或几个 blob，纠删码的作用远不止于安全保障。

背景：子集健全性

在本文中，我们将比较不同编码方案（一维和二维）的效率，假设它们都能达到相同的安全级别。为了使比较更有意义，我们首先需要清楚地理解在 DAS 环境中“安全”的含义。

我们考虑的安全概念被称为子集健全性，并考虑了自适应对手。该概念在《DAS基础》论文中作为定义2正式引入，它也是PeerDAS安全原理的基础。

直观地讲，子集健全性模型模拟了一个强大的对手，他会观察大量n个客户端/节点的查询。然后，对手可以自适应地决定显示哪些符号、隐藏哪些符号，从而有效地构建每个节点看到的视图。对手还会选择一小部分节点（例如， \epsilon n \leq n ϵ n ≤ n ，其中\epsilon > 0 ϵ > 0 ），并试图欺骗这些节点，使其相信数据完全可用。值得注意的是，这种选择可能取决于节点发出的查询。然后，我们考虑对手赢得这场游戏的概率p p ，即

• \epsilon n ϵ n个节点全部接受，并且
• 数据并不完全可用；也就是说：人们无法从查询中重建数据。

为了达到我们的目的，我们希望p p最多为2^{-30} 2 − 30 （对于任何对手）。下面，我们将根据n n 、 \epsilon ϵ和编码方案设置每个节点的查询次数k k ，以保证p \leq 2^{-30} p ≤ 2 − 30 。

\epsilon ϵ的影响和选择：
上面描述的安全概念由\epsilon \in (0, 1] ϵ ∈ ( 0 , 1 ]参数化，它模拟了对手试图欺骗的节点比例。从正式定义和简单的密码学简化来看，给定\epsilon ϵ （具有固定的n n ）的子集健全性意味着任何更大的\epsilon' \geq \epsilon ϵ ′ ≥ ϵ的子集健全性。换句话说：如果对手无法欺骗\epsilon ϵ比例的节点，那么它肯定无法欺骗更大比例的\epsilon' ϵ ′ 。

但这与整体共识协议有何关系？假设我们知道攻击者最多只能欺骗ε ϵ比例的节点。每个被欺骗的节点实际上在共识过程中充当一个额外的恶意节点。因此，当使用数据可用性抽样时，攻击者最多可以获得额外 ε ϵ比例的明显恶意节点。

例如，如果没有 DAS 的共识可以容忍最多<{1}/{3} < 1 / 3 个恶意节点，那么有了 DAS，系统现在只能容忍最多<{1}/{3} - \epsilon < 1 / 3 − ϵ 个恶意节点。

因此，在实际操作中，我们必须选择较小的\epsilon ϵ ，比如\epsilon = 1\% ϵ = 1 % ，以确保对手的影响可以忽略不计。

二、PeerDAS——一维构造

在本节中，我们将解释PeerDAS的工作原理，它将包含在Fusaka升级中。我们还将解释单元级消息传递如何实现部分重建。

工作原理

我们描述了如何编码数据以及客户端如何进行查询，而忽略了与“加密层”相关的所有内容，例如承诺和开口。

一个blob是由m个单元组成的集合，每个单元包含f个字段元素。在 PeerDAS 当前的参数设置中，每个单元包含f = 64个字段元素，每个 blob 包含m = 64个单元。为了考虑不同的单元大小，我们令fm = 4096为常数（即数据大小固定） ，并在f ∈ { 64,32,16,8 }之间变化，即m = 4096 / f 。

要对单个 blob 进行编码，需要使用速率为1/2 1/2的Reed -Solomon 码对其进行扩展，从而得到2m 2 m个单元，或者等效地得到2fm = 8192 2 f m = 8192 个字段元素。在 PeerDAS 中，我们将此编码过程分别应用于b b 个blob，并将扩展后的 blob 视为b \times 2m b × 2 m个单元矩阵中的行。

客户端现在查询该矩阵的整列，也就是说，它们尝试一次性下载b个单元。这意味着“符号”或我们的纠删码是扩展 blob 矩阵的列。从这些列中的任意m个列，都可以重建整个矩阵，从而重建数据。

支持采样功能的具体网络基础设施是列的 GossipSub 主题，即只有对特定样本（= 列）感兴趣的节点参与的子网络。

部分重建

正如预期的那样，当前的PeerDAS设计不支持部分重建。然而，即使是这样的一维编码，原则上也可以支持此功能，当它独立应用于多个blob时，就像在PeerDAS中一样。事实上，通过使用小于列的垂直单位（例如单元格），当然可以仅重建完整矩阵的部分内容，例如单独的行或行组。这带来了两个挑战：

1. 部分重新播种：当一个节点重建单行时，它不会重建任何完整的样本（列），但它仍然需要能够将重建的数据贡献回网络。
2. 获取足够的单元进行重建：当仅对列进行采样时，重建能力要么全部，要么全部不重建，也就是说，一个节点要么获得足够的列来重建整个矩阵，要么无法重建矩阵的任何部分。换句话说，只有超节点才能参与重建。我们希望节点能够做到这一点，同时仍然只下载整个数据的一小部分。

有一些众所周知的方法可以解决这些问题，这些方法可以让我们进行部分重建：

1. 单元级消息传递：使节点能够交换单元而不是整列，以便重建行的节点可以逐个单元地重新播种，至少在它们参与的列主题中是这样。
2. 行主题：有些节点也尝试通过参与行主题下载部分行，并配备单元级消息传递功能。至关重要的是，这并非采样，获取多少行并不涉及安全隐患，因此即使只参与一个行主题也足够了。事实上，在一维结构中，对行进行采样毫无意义，因为不存在垂直冗余。行主题的目的仅仅是使列主题中的单元能够流入其中并实现行向重构，而无需任何超节点。重构后的单元随后可以从行主题流入所有列主题，同样无需任何单个节点参与所有列主题。

注意：缺乏垂直冗余意味着我们需要每个行主题都能成功执行其重建任务。即使只有一个行主题失败（例如，由于仅限于该主题的网络级攻击），整个重建也无法完成。

样本数量

现在让我们确定PeerDAS每个客户端的样本数量k 。如上所述，我们希望选择k ，使得攻击者破坏子集健全性的概率p最多为2^{-30} 2 − 30 。

PeerDAS 的安全性已在这里和这里进行了广泛的分析。后者的工作建立在这里的安全框架之上，并且可以通过结合引理 1 和引理 3得出子集健全性的具体界限。最终，所有这些得出了相同的子集健全性界限，即：

p \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot (\frac{m-1}{2m})^{kn\epsilon} \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot 2^{-kn\epsilon}. p ≤ ( n n ϵ ) ⋅ ( 2米米− 1​ ) ⋅ （米− 1 2米) k n ϵ ≤ ( n n ϵ ) ⋅ ( 2米米− 1​ ) ⋅ 2 − kn ϵ 。​

直观地讲，第一个二项式表示对手自由且自适应地挑选n\epsilon n ϵ个节点来欺骗的能力，第二个二项式表示对手选择m-1 m − 1 个符号来提供给这些节点，最后一个项是所有样本最终都出现在编码的可用部分中的概率。

如果我们希望p \leq 2^{-30} p ≤ 2 − 30且n,m,\epsilon n , m , ϵ已知，我们需要设定

k \geq \frac{1}{n\epsilon} \left( \log_2 \binom{n}{n\epsilon} + \log_2 \binom{2m}{m-1} + 30 \ right ) k≥1nϵ （日志2 ( n n ϵ ） + log 2 （ 2米− 1​ ） + 30 ） 。

以下是计算k k的代码：

 from math import comb, log2, ceil # used later from tabulate import tabulate # used later import numpy as np # used later import matplotlib.pyplot as plt # used later def min_samples_per_node ( n: int , m: int , r: int = 2 , eps: float = 0.01 ): """Finds the smallest integer k such that k samples per nodeachieve security of 30 bits for the 1D construction.Inputs:n: total number of nodesm: number of symbols in original datar: inverse coding rate (total symbols = r*m), default=2eps: fraction of nodes to be fooled (0 < eps <= 1), default=0.01Returns:Smallest integer k satisfying the bound""" neps = int (n * eps)binom_n = comb(n, neps)binom_m = comb(m*r, m- 1 )log2_binom = log2(binom_n) + log2(binom_m)k = -(log2_binom + 30 )/(n*eps*log2( 1 /r)) return ceil(k)

III. 2D 构造

PeerDAS 的替代方案是二维构造，这已经在（此处、 此处和此处）讨论过了。该构造基于 Reed-Solomon 码的张量编码，并已在此处第 8 节进行了分析。它支持一种自然形式的部分重建。

工作原理

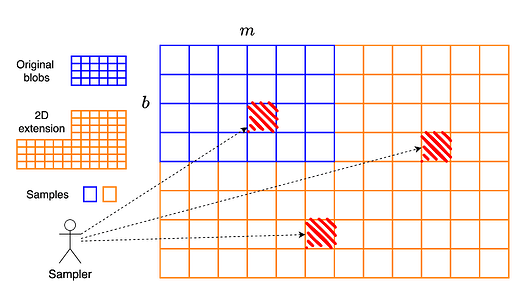
我们可以将 PeerDAS 视为将一个b \times m b × m矩阵（ b b 个blob，每个 blob 有m m 个cell）水平扩展为一个b \times 2m b × 2 m 个cell 矩阵。等效地，这是一个由场元素组成的b \times 2mf b × 2 m f矩阵，其中每个 cell 包含f f个场元素。由于扩展仅沿水平轴进行，因此 PeerDAS 被称为一维结构。

在二维构造中，我们按如下方式进行：从 PeerDAS 中导出的b \times 2mf b × 2 m f矩阵开始，然后使用另一个速率为1/2 1 / 2的 Reed–Solomon 码垂直扩展每一列。最终得到一个大小为2b \times 2mf 2 b × 2 m f的矩阵，或者等效地，一个由单元组成的2b \times 2m 2 b × 2 m矩阵。

与 PeerDAS 的一个关键区别在于，在二维结构中，客户端采样的是单个单元格，而不是整列。也就是说，代码的一个符号是一个单元格，而不是一整列。

图片2848×1592 148 KB

部分重建

二维构造中的重建自然是一个涉及几个子过程的过程：

• 只要同一行中至少有m个单元格可用，就可以完全重建该行。
• 类似地，只要同一列中至少有b个单元格可用，就可以重建该列。

这种局部性意味着不需要一个中心超级节点来重建整个数据集。相反，只要有足够多的节点能够独立地重建特定的行或列，就能以去中心化的方式实现相同的目标。

样本数量

同样，我们希望确定每个客户端的样本数量k k ，以实现p \leq 2^{-30} p ≤ 2 − 30形式的安全性。为此，我们需要在二维结构中确定p p的上限。

使用DAS 基础论文中的工具，我们可以获得边界

p \leq \binom{n}{n\epsilon}\cdot \binom{4mb}{4mb - (b+1)(m+1)} \cdot (\frac{4mb - (b+1)(m+1)}{4mb})^{kn\epsilon} = \binom{n}{n\epsilon}\cdot \binom{4mb}{(b+1)(m+1)} \cdot (1-\frac{(b+1)(m+1)}{4mb})^{kn\epsilon}. p ≤ ( n n ϵ ) ⋅ ( 4米b 4米b − ( b + 1 ) (米+ 1 ) ) ⋅ ( 4米b − ( b + 1 ) (米+ 1 ) 4米b ) kn​