通过Gas退款超频区块
TL;DR:存储清理退款很有价值,但可能会使区块gas数值膨胀 - 保留给用户,但不计入区块已使用的gas - EIP-7778恢复准确的链上gas核算。
以太坊的gas机制旨在准确反映计算资源消耗。为鼓励用户保持状态清洁和可管理,以太坊在存储槽重置为零时授予gas退款。尽管这在减少状态膨胀方面有效,但这些退款目前使gas核算变得复杂,使得看起来区块消耗的资源比实际消耗的少。
[后续内容保持原有翻译风格,只展示开头部分]n = ⌊log(21,000/45,000,000)/log(0.2)⌋ + 1
n = ⌊log(21,000/45,000,000)/log(0.2)⌋ + 1
(⌊x⌋表示向下取整函数,给出小于等于x的最大整数。)
总计算Gas
累加到第n-1步的所有计算Gas:
总Gas = 初始Gas + 初始Gas * r + 初始Gas * r² + ... + 初始Gas * r^(n-1)
总Gas = 初始Gas(1 + r + r² + ... + r^(n-1))
使用几何级数公式:
1 + r + r² + ... + r^(n-1) = (1 - r^n) / (1 - r)
得到:
总Gas = 初始Gas × (1 - r^n) / (1 - r)
代入数值:
- 初始Gas = 45,000,000
- r = 0.2
- 最小Gas = 21,000
计算n:
n = ⌊log(21,000/45,000,000)/log(0.2)⌋ + 1 = ⌊4.766⌋ + 1 = 5
计算总Gas:
G_{\text{total}} = 45,000,000 \times \frac{1 - (0.2)^5}{1 - 0.2} = 56,232,000
Gtotal=45,000,000×1−(0.2)51−0.2=56,232,000
这表明从初始gas限额增加了约25%,突显了当前退款如何显著扭曲区块gas核算。
示例合约
这些合约可能看起来像这样:
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
contract Refundooor {
mapping(uint256 => uint256) private storageSlots;
/// @notice 从`startKey`开始预填充`maxSlots`个键
function chargeStorage(uint256 startKey, uint256 maxSlots) external {
for (uint256 i = 0; i < maxSlots; i++) {
storageSlots[startKey + i] = startKey + i + 1;
}
}
/// @notice 无条件清除恰好MAX_LOOPS个插槽(无检查)
fallback() external {
assembly {
let base := storageSlots.slot
mstore(0x20, base)
// MAX_LOOPS * ~5,109 gas/iter ≈ 45 000 000 gas
let MAX_LOOPS := 8805
for { let i := 0 } lt(i, MAX_LOOPS) { i := add(i, 1) } {
// 计算键 = i 的存储插槽
mstore(0x0, i)
let s := keccak256(0x0, 0x40)
// 无条件写入零
sstore(s, 0)
}
}
}
}- 首先通过写入空存储插槽来"充值"合约。
- 其次,调用合约的回退函数,将8805个存储插槽设置为零。
查看这个在Holesky上最大化
SSTORE操作数量的示例交易。
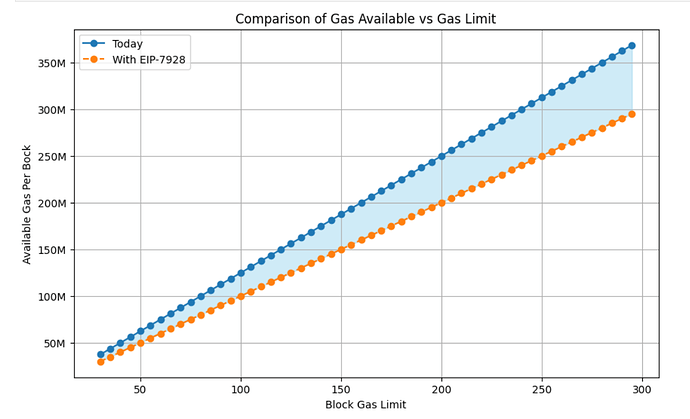
最终,"走私"的gas与区块gas限额呈线性扩展。在100M gas时,一个区块可以包含125M gas的实际工作。
建议的变更:将交易退款与区块gas核算分离
EIP-7778提议保留用户级退款以激励高效存储管理,但从区块级gas核算中移除这些退款。这确保区块gas使用准确反映实际资源消耗。
实施该EIP的好处是:
- 提高可预测性:区块的实际工作保持在预期限制以下。
- 增加网络稳定性:无论最坏情况如何,都能降低拒绝服务(DoS)风险。
- 保留用户激励:用户保持清理状态的动力。
EIP-7778干净地将用户激励与区块范围的资源约束分离,使区块gas使用更接近实际执行的工作。