从 Pedersen 承诺范围证明中移除配对、防弹证明或 ZKP

TL;DR

简化范围证明。在 EVM 上验证基于 Pedersen 承诺的隐私币的范围证明，仅需 6 个 ECMUL 和 3 个 ECADD（37,000 Gas）。首次设置和承诺需要 zkSNARK，但之后成本将降至最低。客户端每次生成交易时，也无需进行 ZKP 计算。

包含安全证明的完整论文： https://eprint.iacr.org/2025/1811.pdf

步骤：

G、H、B 是曲线上的独立点。

为每个证明者（代币发送者）进行一次性设置

1. 采样 a ← Zq 并设置公共锚点 U = aB。
2. 使用曲线上的点构建一棵 Merkle 树。对于每个 X ∈ {1, . . . , 2 n}，定义叶子节点 aXG
3. 使用 NIZK 上链，证明由 aXG 组成的树的 Merkle 根。（预范围证明）

无标题演示文稿 (11) 960×540 20.3 KB

证明（发送令牌时）

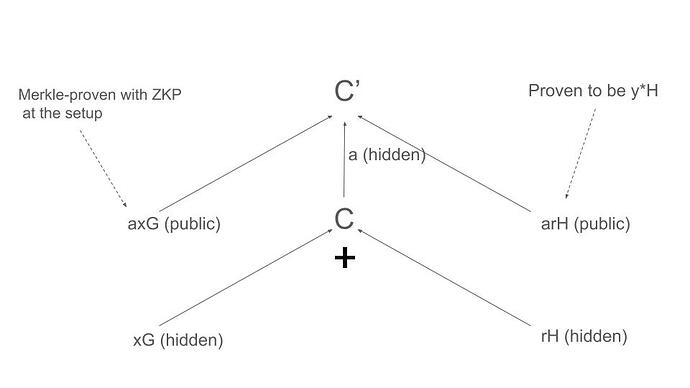
1. 做出 Pedersen 承诺 C = xG + rH，其中代币数量为 x，隐藏 r。（x、r、xG 和 rH 不应暴露）
2. 提交 C, C' = aC, axG 及其 Merkle 证明、(U, B) 和 (C', C) 的 Chaum-Pedersen DLEQ 证明、arH 和 Schnorr 协议的 (arH, H) 证明

验证（C 和 x 是否在 EVM 的范围内）

1，使用 Chaum-Pedersen DLEQ 检查 (U, B) 和 (C', C) 是否具有相同的离散
2. 使用 Schnorr 协议或 ECDSA 检查证明者是否可以从 H 得出 arH。
3. 在设置树中检查axG的Merkle Proof。
4. 检查 C' = axG + arH

## 为什么需要 Chaum-Pedersen DLEQ 和 U=aB
如果我们使用 Schnorr 协议或 ECDSA 来检查 (C', C) 的关系，恶意证明者可以使 C' = yC 和 C = (bigX)G + rH，其中 y = ax/(bigX)。yrH 也将被验证。

如何让树变小

用随机数创建一棵包含所有金额的树会有点挑战性。用有限的随机数创建一棵点树，用标量乘以叶子节点，并在链上添加一个点，会很有帮助，因为没有人能从树曲线上的点猜出随机数。