私人多重签名 v0.1

avatar
Ethereum Research
10-16
本文为机器翻译
展示原文

这是我花了一段时间才实现的。虽然不完美，但已经尽可能地实现了隐私保护的多重签名。期待您的反馈！

请查看我的其他相关研究论文： 《Confidential Wrapped Ethereum》和《ZEX：Confidential Peer-to-Peer DEX》 。

另外，请看一下宏伟的以太坊隐私路线图。

抽象的

本文提出了一种基于零知识 (ZK) EVM 的多重签名钱包的实用实现方法，以保护集体决策的隐私和机密性。该方法结合了三个核心特性：用于匿名性的 Merkle 树成员身份证明；用于无偏见决策的聚合 ECC ElGamal 加密，以确保参与者投票的机密性；以及用于在密钥推导和消除中心化可信实体时实现非交互性的分布式密钥生成 (DKG)。

所提出的解决方案由 Solidity 智能合约和零知识证明电路组成。前者充当账户工厂的角色，并充当用户与之交互以创建多重签名和执行集体提案的实际账户。后者负责检查用户是否属于多重签名集，并验证他们是否执行提案的决定，且不透露中间结果。

所提出方法的缺点是，所有多重签名参与者必须对提案进行投票才能计算其结果。

1. 简介

公链的透明度带来了诸多优势，包括增强操作的可追溯性、执行的可验证性以及数据开放性，使每个人都能访问。然而，它在多方决策方面也带来了独特的挑战，尤其是在保护隐私和防止投票偏见方面——而这正是安全公正的多重签名钱包的基本要素。

目标是创建一个简单的、无需许可的多重签名，它不会透露任何有关其成员的信息，并向多重签名选民保证他们的选票是秘密的，并且他们的选择不会受到早期参与者投票方式的影响。

多重签名将允许用户加入/退出成员列表、配置“签名阈值”以及执行集体批准的交易，且几乎不会损害隐私。此外，在成员列表中的所有用户都投票之前，用户可以在不了解个人投票或结果的情况下对提案进行投票支持或反对。

当然，重要的限制是，最后一位投票参与者将能够在投票和披露投票之前解密并查看正在进行的提案方向。

2. 规格

2.1. 申请流程

在深入技术探讨之前，有必要先了解一下整体架构并理解基本的应用程序流程。本文提供了多重签名钱包创建、提案创建以及包含提案投票的通用多重签名交易执行流程。

2.1.1. 多重签名创建

该应用程序的基石是多重签名钱包。用户与应用程序交互时，会根据允许投票者的列表创建多重签名，以满足其业务逻辑。

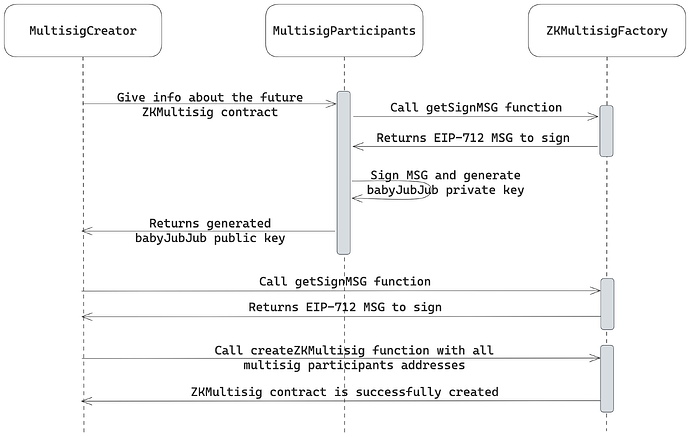
多重签名创建流程如下图所示：

图 1：ZKMultisig 合约创建流程
图1：ZKMultisig合约创建流程3159×2003 245 KB

  1. 创建流程始于用户（钱包创建者）收集待添加到允许列表中的投票者的公钥。由于多重签名使用零知识证明来保护隐私，所有用户在使用应用程序之前都必须创建一个特殊的 babyJubJub 密钥对，作为其唯一标识符。

    要创建这些密钥，用户需要使用其以太坊（ECDSA）私钥对 EIP-712 结构化消息进行签名，并对获得的签名进行哈希处理。生成的哈希值即为 babyJubJub 私钥。

    用户可以选择签署唯一消息以获取他们愿意参与的每个多重签名的唯一公钥（增加隐私），或者使用“默认”消息坚持使用单个公钥以在整个平台上使用（可能更好的用户体验）。

  2. 获取所有必要的 babyJubJub 公钥后，钱包创建者会调用ZKMultisigFactory智能合约上的钱包创建函数，提供所有需要添加到允许列表中的公钥。多重签名机制在底层将参与者信息存储在稀疏 Merkle 树 (SMT) 数据结构中，从而实现零知识证明的成员资格证明和低成本的列表维护。

  3. 多重签名钱包部署后，其成员可以通过生成 ZK 成员资格证明并应用 EdDSA 盲注器来创建提案并对其进行投票，以实现决策不可重用性。

通过所描述的方法，我们可以通过确定性密钥派生函数（KDF）将用户的真实“钱包地址”抽象为 babyJubJub 地址，从而为用户实现完全隐私，并将确定决策地址的概率从 1 降低到1/N 1 / N ，其中N N是多重签名成员的数量。

2.1.2 提案创建

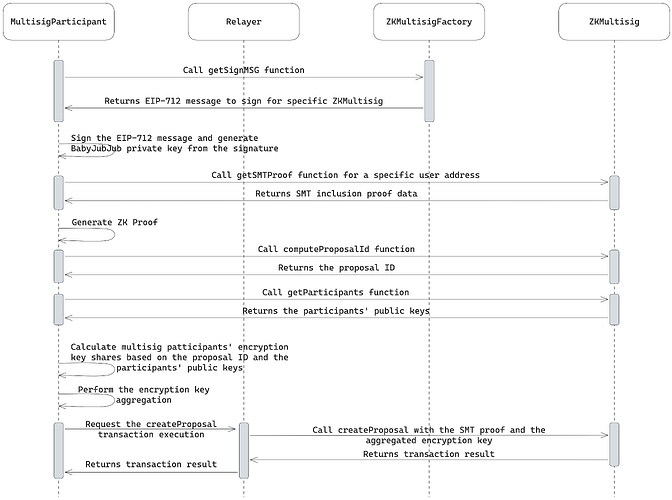
提案创建流程如下图所示：

图 2：多重签名提案创建流程
图 2：多重签名提案创建流程4360×3240 434 KB

  1. 提案创建者（来自多重签名允许列表中的用户）通过从“多重签名钱包创建”步骤中确定性地恢复 babyJubJub 密钥对来登录应用程序。

    KDF 算法保持不变。从ZKMultisigFactory获取 EIP-712 结构化消息，然后对其进行签名，并对签名进行哈希运算，计算出 babyJubJub 私钥。

  2. 用户生成一个 ZK 证明，该证明通过 SMT 包含证明无需许可地验证他们在多重签名中的成员资格。

  3. 提案创建者计算提案的 ID，用于生成一次性聚合加密密钥。

  4. 创建者根据提案 ID 和参与者的 babyJubJub 公钥，使用 KDF 以非交互方式计算每个多重签名参与者的加密密钥份额。

  5. 在计算出所有加密密钥份额后，创建者将它们聚合成最终的加密密钥。

  6. 提案创建者通过中继器调用createProposal函数，提供 SMT 包含证明和聚合密钥，以便进一步用于投票加密。

提案创建后，多重签名参与者可以开始投票。

2.1.3. 对提案进行表决

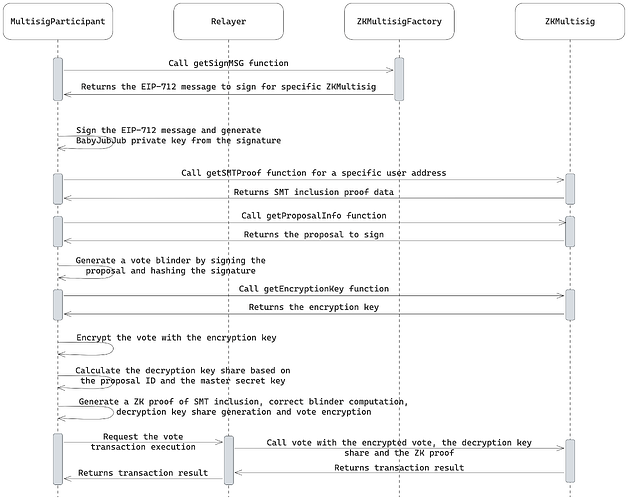
提案投票流程如下图所示：

图 3：多重签名提案投票流程
图 3：多重签名提案投票流程4120×3280 468 KB

  1. 从合同中获取 SMT 包含（Merkle）证明，以表明用户是多重签名的成员。

  2. 用户使用 babyJubJub 私钥对要投票的提案进行签名，并通过对获得的 EdDSA 签名进行哈希运算来生成盲注。该盲注用于验证用户之前是否曾对同一提案进行投票。

  3. 用户获取提案的加密密钥。

  4. 收到的临时加密密钥用于加密他们的投票。

  5. 根据提案 ID，用户使用其 babyJubJub 私钥和 KDF 计算解密密钥份额。

  6. 在计算完所有需要的数据后，多重签名参与者通过中继器调用vote功能，提供加密投票、解密密钥共享和 ZK 证明。

  7. 智能合约将提供的解密密钥份额添加到可聚合的最终解密密钥中，并将投票设置为成功投票。

2.1.4 投票披露和提案执行

只有当最后一位参与者投票后，解密密钥才算完整，并可用于揭示投票结果。这通过调用reveal函数来完成。该函数解密汇总的投票，并根据投票结果更改提案状态。如果“赞成”票数超过“签名阈值”，则该提案被设置为“接受”并可执行；否则，则设置为“拒绝”。

下图说明了投票披露过程，将解密和执行逻辑封装到单个函数revealAndExecute中。

图 4：多重签名提案投票揭示流程
图 4：多重签名提案投票揭示流程2390×1540 169 KB

2.2. 加密数学

本节提供了协议中使用的投票加密逻辑的数学基础。

2.2.1. 椭圆曲线算术运算

在本文档的上下文中，某些操作是在椭圆曲线上执行的，并且涉及不同于传统算术的特定数学运算：

  • 点加法P + Q P + Q ，其中P P和Q Q是椭圆曲线上的点，按照定义的群运算逻辑执行。
  • 标量乘法k \times P k × P ，其中k k是标量， P P是椭圆曲线上的一个点，涉及将点P P与自身相加k k次。
  • 点减法P - Q P − Q ，其中P P和Q Q是椭圆曲线上的点，并且与P + (-Q) P + ( − Q )相同，其中-Q − Q是点Q Q的逆。

2.2.2. 加密密钥的 KDF

该协议使用隐形密钥方案 CoM17 [1] 作为确定性密钥分配函数 (KDF)。该方案能够根据主密钥生成唯一的密钥共享，用于加密和解密每个提案的投票。

主密钥对必须满足以下条件：

pk = sk \times G ， pk = sk × G ，

其中pk p k — 主公钥，
sk s k — 主密钥，
G G — 椭圆曲线上的基点。

在创建钱包时生成的 babyJubJub 密钥对将用作主密钥对，ElGamal 加密密钥和解密密钥由此派生。密钥派生过程如下所述。

首先，根据提案 ID 计算挑战。需要注意的是，多重签名机制有意省略了提案的增量枚举，以防止零知识证明重放和抢先交易攻击。这是通过要求提案创建者签署其所创建提案的挑战来实现的。提案 ID 和挑战的确定性计算方式如下：

 proposalId = keccak256(abi.encode(target, value, data, salt));challenge = poseidon(uint248(keccak256(abi.encode(chainid, zkMultisigAddress, proposalId))));

令r r等于挑战， R R为挑战点：

R = r \times G R = r × G

加密密钥共享的推导如下：

P_i = poseidon(r \times pk_i) \times G + pk_i P i = p o s e i d o n ( r × p k i ) × G + p k i

相应地，解密密钥份额推导如下：

x_i = (poseidon(sk_i \times R) + sk_i) \mod n x i = ( po o s e i d o n ( s k i × R ) + s k i )模组n

其中n n — 椭圆曲线的阶。

密钥派生方案的一致性可以通过以下方式证明：

P_i = x_i \times G = (poseidon(sk_i \times R) + sk_i) \times G = P i = x i × G = ( p o s e i d o n ( s k i × R ) + s k i ) × G =
= poseidon(sk_i \cdot r \ times G ) \ times G + sk_i \ times G = poseidon ( r \ times pk_i ) \ times G + pk_i = poseidon ( ski⋅r × G ) × G + ski × G = poseidon ( r × pki ) × G + pki

2.2.3. ECC ElGamal加密方案

该协议利用 ElGamal 加密方案 [2] 的椭圆曲线密码学 (ECC) 修改来加密并解密多重签名投票。

聚合加密密钥P P是通过对所有加密密钥份额求和计算得出的椭圆曲线上的一个点：

P = \sum_{i=1}^N P_i， P = ∑ N i = 1 P i ，

其中N N — 多重签名参与者的数量，
P_i P i — 加密密钥共享（椭圆曲线点）。

参与者的投票被映射到椭圆曲线上的点M M 。生成点G G用作“赞成”票，无穷远点用作“反对”票。选择一个满足0<k< n的随机值k k 。之后，计算密文 ( C_1 C 1 , C_2 C 2 )：

C_1 = k \times G C 1 = k × G
C_2 = M + k \times P C 2 = M + k × P

要解密投票，首先计算聚合解密密钥份额：

x = \sum_{i=1}^N x_i \mod n, x = ∑ N i = 1 x i模组n ，

其中n n — 椭圆曲线的阶，
x_i x i — 解密密钥共享（标量）。

然后使用计算出的聚合解密密钥x x恢复消息点M M ：

M = C_2 - x \times C_1 M = C 2 − x × C 1

ECC ElGamal方案中密钥聚合的一致性可以证明如下：

P = \sum_{i=1}^N P_i = \sum_{i=1}^N x_i \times G P = ∑ N i = 1 P i = ∑ N i = 1 x i × G

D = x \times C_1 = \sum_{i=1}^N x_i \times C_1 = \sum_{i=1}^N x_i \cdot k \times G = k \times (\sum_{i=1}^N x_i \times G) = k \times P D = x × C 1 = ∑ N i = 1 x i × C 1 = ∑ N i = 1 x i ⋅ k × G = k × ( ∑ N i = 1 x i × G ) = k × P

M = C_2 - D = M + k \times P - k \times P M = C 2 − D = M + k × P − k × P

2.2.4. 投票的同态聚合

使用点G和无穷远点作为投票，可以同态地形成累积投票结果，将每次投票期间的加密投票相加：

SC_1 = \sum_{i=1}^N C_{1_i} S C 1 = ∑ N i = 1 C 1 i
SC_2 = \sum_{i=1}^N C_{2_i} S C 2 = ∑ N i = 1 C 2 i

解密总和得到聚合结果T T ：

T = \sum_{i=1}^N M_i = SC_2 - x \ times SC_1 T = ∑ N i = 1 M i = SC 2 − x × SC 1

解密后的总数T T等于v \times G v × G ，其中v v是投票“支持”该提案的选民总数。

为了揭示投票结果，多重签名参与者必须循环遍历链下可能的标量值v_i v i ，其中0 \leq v_i \leq N 0 ≤ v i ≤ N ，以找到满足以下等式的值：

v_i \times G = T v i × G = T

然后他们将这个值提交给智能合约，在那里检查上述等式。

  • 如果v < signaturesQuorum v < s i g n a t u r e s Q u o r u m ，则表示没有足够的参与者对该提案投“赞成票”，其状态设置为“拒绝”；
  • 如果v \geq signaturesQuorum v ≥ sign u n a t u r e s Q u o r u m ，则有足够多的参与者对该提案投了赞成票，其状态设置为“已接受”。

2.2.5. 加密密钥链上计算

当提案被创建时，必须检查聚合加密密钥是否是根据各个公钥和质询正确计算出来的。

由于该值是公开可计算的，因此可以通过循环遍历参与者的主公钥并得出其加密份额来在智能合约上进行评估。然而，这种方法并非最优，可以通过引入累积公钥（表示所有参与者主公钥的总和）来改进。该密钥存储在智能合约中，并且每次更新成员列表时都必须更新。

无需为每个参与者单独计算加密密钥份额：

P_i = poseidon(r \times pk_i) \times G + pk_i P i = p o s e i d o n ( r × p k i ) × G + p k i

只需计算哈希部分并将其添加到先前哈希的总和中就足够了，从而减少循环内的操作数：

sumHash = sumHash + poseidon ( r \ times pk_i ) s u m H a s h = s u m H a s h + poseidon ( r × p k i )

然后可以按如下方式计算聚合加密密钥：

aggKey = sumHash \times G + cumulativePk a g g K e y = s u m H a s h × G + c u m u l a t i v e P k

2.3. 功能

本节提供智能合约和电路的技术描述。本节概述了实现可行原型所需的组件支持功能。

2.3.1. ZKMultisigFactory

该应用程序中有两个合约： ZKMultisigFactory和ZKMultisig 。工厂合约用于创建多重签名钱包并生成密钥派生过程所需的 EIP-712 消息。ZKMultisig 是ZKMultisig本身的实现。

ZKMultisigFactory接口定义如下：

 interface IZKMultisigFactory {event ZKMultisigCreated(address indexed zkMultisigAddress,uint256[2][] initialParticipants,uint256 initialQuorumPercentage);function createZKMultisig(uint256[2][] calldata participants,uint256 quorumPercentage,uint256 salt) external returns (address);function computeZKMultisigAddress(address deployer,uint256 salt) external view returns (address);function getKDFMSGToSign(address zkMultisigAddress) external viewreturns (bytes32);function getDefaultKDFMSGToSign() external view returns (bytes32);function isZKMultisig(address multisigAddress) external view returns(bool);}

ZKMultisigFactory并不直接部署钱包，而是部署 ERC-1967 代理。此外，它采用 create2 方法预先建立 KDF 消息，以确保钱包地址的确定性。

create2中的salt定义如下：

 realSalt = keccak256(abi.encode(msg.sender, salt));

用户可以决定签署哪个 KDF 消息：

  • 每个钱包的唯一消息（增加隐私假设）；
  • 默认的（可能用户体验更好）。

返回消息的结构可以在第 2.3.6 节中找到。

2.3.2 ZKMultisig

ZKMultisig是一个实现多重签名功能的合约。该功能包括多重签名参与者的管理、法定人数设置、提案的创建、投票及其执行。ZKMultisig ZKMultisig定义如下：

 import "@solarity/solidity-lib/libs/data-structures/SparseMerkleTree.sol";interface IZKMultisig {enum ProposalStatus {NONE,VOTING,ACCEPTED,REJECTED,EXPIRED,EXECUTED}struct ZKParams {uint256[2] a;uint256[2][2] b;uint256[2] c;uint256[] inputs;}struct ProposalContent {address target;uint256 value;bytes data;}struct ProposalInfoView {ProposalContent content;ProposalStatus status;uint256 proposalEndTime;uint256 votesCount;uint256 requiredQuorum;}event ProposalCreated(uint256 indexed proposalId, ProposalContent content);event ProposalVoted(uint256 indexed proposalId, uint256 voterBlinder);event ProposalExecuted(uint256 indexed proposalId);function addParticipants(uint256[2][] calldata participantsToAdd) external;function removeParticipants(uint256[2][] calldata participantsToRemove) external;function updateQuorumPercentage(uint256 newQuorumPercentage) external;function create(ProposalContent calldata content,uint256 duration,uint256 salt,ZKParams calldata proofData) external returns (uint256);function vote(uint256 proposalId,bytes calldata encryptedVote,uint256 decryptionKeyShare,ZKParams calldata proofData) external;function reveal(uint256 proposalId, uint256 approvalVoteCount) external;function execute(uint256 proposalId) external;function revealAndExecute(uint256 proposalId,uint256 approvalVoteCount) external;function getPerticipantsSMTRoot() external view returns (bytes32);function getParticipantsSMTProof(bytes32 publicKeyHash)external view returns (SparseMerkleTree.Proof memory);function getParticipantsCount() external view returns (uint256);function getParticipants() external view returns (uint256[2][] memory);function getProposalsCount() external view returns (uint256);function getProposalsIds(uint256 offset, uint256 limit)external view returns (uint256[] memory);function getQuorumPercentage() external view returns (uint256);function getEncryptionKey(uint256 proposalId) external viewreturns (uint256[2] memory);function getProposalInfo(uint256 proposalId) external viewreturns (ProposalInfoView memory);function getProposalStatus(uint256 proposalId) external viewreturns (ProposalStatus);function getProposalChallenge(uint256 proposalId)external view returns (uint256);function computeProposalId(ProposalContent calldata content,uint256 salt) external view returns (uint256);function isBlinderVoted(uint256 proposalId,uint256 blinderToCheck) external view returns (bool);}

在createProposal函数中，验证给定提案的 ElGamal 加密密钥聚合至关重要。智能合约必须循环遍历活跃成员的主公钥，得出他们的加密密钥份额，然后将其聚合到加密密钥中（参见 2.2.5 节）。

2.3.3 提案创建电路

本文中的每个参数都旨在可证明并与零知识电路兼容。提案创建证明的电路信号列表如下：

公共信号：

  • SMT 根（输入）；
  • 提案 ID（输入）。

私人信号：

  • 主密钥；
  • 主公钥[可选]；
  • SMT 包容性证明。

利用这些信号，电路必须具有以下约束：

  • 所提供的主密钥确实是所提供的主公钥的密钥。
  • 主公钥属于 SMT，锚定于 SMT 根。

2.3.4. 提案投票电路

提案投票证明的电路信号列表如下：

公共信号：

  • 用户盲区（输出）；
  • 解密密钥共享（输出）；
  • 加密点C_1 C 1 （输出）；
  • 加密点C_2 C 2 （输出）；
  • 聚合加密密钥（输入）；
  • 提案挑战（输入）；
  • SMT 根（输入）。

私人信号：

  • 主密钥；
  • 主公钥[可选]；
  • EdDSA 主控对挑战进行签名；
  • 实际投票：点G G或inf i n f ；
  • 随机加密值k k ；
  • SMT 包容性证明。

利用这些信号，电路必须具有以下约束：

  • 所提供的主密钥确实是所提供的主公钥的密钥。
  • 主公钥属于 SMT，锚定于 SMT 根。
  • 挑战的 EdDSA 主签名根据主公钥进行验证。
  • 签名的波塞冬哈希等于用户盲注。
  • 根据主密钥和提议挑战，可以正确计算解密密钥份额（参见第 2.2.2 节）。
  • 提供的投票要么等于G G ，要么等于inf i n f 。
  • 给定聚合加密密钥、随机加密值k k和投票，加密已正确执行（参见第 2.2.3 节）。

2.3.5. 密钥衍生函数

密钥派生函数 (KDF) 是一种根据某个输入确定性地创建 babyJubJub 私钥的函数。在我们的例子中，输入是 EIP-712 格式消息的以太坊 ECDSA 签名。

KDF定义如下：

 message = getKDFMSGToSign() or getDefaultKDFMSGToSign();signature = eth_signTypedData_v4(message);privateKey = keccak256(keccak256(signature));

请注意，切勿泄露签名，因为私钥直接来源于签名。

2.3.6. KD EIP-712 消息

为了创建密钥派生 EIP-712 消息，需要使用包含合约ZKMultisig地址的 KDF 消息类型哈希。由于网络和合约信息已包含在标准 EIP-712 域结构中，因此这已足够。

 bytes32 KDF_MSG_TYPEHASH = keccak256("KDF(address zkMultisigAddr)");bytes32 kdfStructHash = keccak256(abi.encode(KDF_MSG_TYPEHASH, zkMultisigAddress));

getKDFMSGToSign()和getDefaultKDFMSGToSign()函数如上所述创建 EIP-712 消息。getDefaultKDFMSGToSign getDefaultKDFMSGToSign()函数使用零地址来构造默认消息。

2.3.7. 中继器

由于上述方法完全独立于交易发送的 EVM 地址，用户可以使用不同的中继器来保持匿名。可以使用协议友好的中继器（例如 GSN），但这需要在前端添加额外的集成逻辑。

3. 基本原理

之所以选择 ElGamal 加密方案 [2] 的 ECC 修改版，是因为它兼容密钥派生函数 (KDF) 和密钥聚合。ElGamal 的非确定性特性（由随机值k k引入）可确保每次加密操作都生成唯一的密文，从而增强了安全性。

为了降低传统解密密钥管理相关的中心化风险（例如在Shamir秘密共享（SSS）方案中，需要在秘密共享之前先确定解密密钥的存在），我们采用了分布式密钥生成（DKG）方法。它提供了一种由每个参与者以去中心化的方式生成解密密钥的机制，确保任何一方在密钥公开之前都无法掌握完整的密钥。

大多数 DKG 协议通过采用可验证秘密共享 (VSS) 来消除对可信方的需求，VSS 要求参与者交互以验证共享的有效性。此过程被替换为在投票时按需验证解密密钥共享的零知识证明。

虽然 DKG 消除了各方之间密钥共享交换的需要，但它仍然需要在提案创建期间发布加密密钥共享。使用确定性 KDF，参与者可以避免交互过程，从而使提案创建者能够异步且独立地聚合最终的加密密钥。

4. 安全考虑和限制

该协议固有的一些安全风险和限制需要考虑：

  • 可信设置。如果使用 Groth16 作为 zk-SNARK 证明系统，则需要对每个电路进行可信设置，并且必须正确执行。

  • 私钥/签名泄露。确保密钥派生 ECDSA 签名的私密性至关重要。babyJubJub 密钥对直接由该签名派生而来，因此签名泄露会导致用户所在的多重签名系统容易受到网络钓鱼/垃圾邮件攻击。

  • 提案抢先交易。即使提案挑战已根据提案内容确定性地得出，仍然有可能利用相同的提案抢先创建提案。这不会直接影响安全性，但应予以注意。

  • 参与者移除僵局。如果被移除的参与者没有投票（这对他们来说很正常），移除提案将失效，而该参与者仍为多重签名成员。一个可能的解决方案是对此类提案进行公开投票。

  • 修改参与者列表。每当有活跃（正在进行）的提案时，在多重签名中添加或删除参与者会非常困难。这样做可能会导致加密方案中使用的密钥不一致。一个可能的解决方案是跟踪此类提案，并仅在没有其他正在进行的提案时才允许创建它们。

  • 最后投票者的优势。由于一旦知道所有解密密钥份额，就可以解密选票，因此最后一位参与者可以在投票之前重建之前的选票。

  • 可扩展性。投票披露和提案结果计算的复杂性与参与者数量成线性关系。

参考

[1] Nicolas T. Courtois 和 Rebekah Mercer. 隐身地址和密钥管理技术
区块链系统。2017 年。网址： https://www.scitepress.org/papers/2017/62700/62700.pdf 。
[2] Neal Koblitz. 椭圆曲线密码系统. 1987. url: https://www.ams.org/journals/mcom/1987-48-177/S0025-5718-1987-0866109-5/S0025-5718-1987-0866109-5.pdf .


相关赛道:
智能合约公链
衍生品
Layer 2
来源
免责声明：以上内容仅为作者观点，不代表Followin的任何立场，不构成与Followin相关的任何投资建议。
喜欢
收藏
评论
相关推荐