感谢@aelowsson 的审阅和反馈。
本分析的目标是了解在增加区块 gas 限制的情况下,以太坊状态(每个完整节点的数据库大小)如何演变,以及重新定价(改变状态字节和突发资源的有效 gas 成本)如何影响状态增长和突发吞吐量。
为了实现这一目标,我们:
- 在三种天然气限制轨迹(基准、激进、保守)下规划国家规模。
- 构建并校准一个简单的等弹性需求模型,用于描述状态创建和突发资源消耗。
- 使用该模型计算新的 EIP-1559 均衡基本费用以及当添加状态的 gas 限制和/或 gas 价格发生变化时产生的每个区块资源份额。
- 报告不同价格弹性范围内的状态需求和突发需求情景对比。
TLDR
- 如果吞吐量增加,而状态创建成本保持相对低廉,则状态规模可以大幅增长。到 2027 年年中,保守方案的总状态规模将达到 686 GiB,基础方案为 859 GiB,而激进方案则为 1.08 TiB。所有这些数值都超过了bloatnet 计划确定的 650 GiB 的关键阈值。
- 我们需要就以太坊在中长期内可接受的状态增长水平达成一致。
- 提高状态创建的 gas 成本会降低所探索的弹性机制下的预期状态增长,但会略微降低突发资源吞吐量。
- 吞吐量损失受突发需求弹性的影响比状态创建成本的影响更大。当突发需求具有价格弹性时,容量翻倍仍然能带来接近线性的吞吐量提升,重新定价的影响很小。
- 如果状态创建需求缺乏弹性,那么提高状态创建成本预计会导致基础费用高于状态不重新定价的情况。如果这种需求富有弹性,则这种效应会逆转。
1. 我们为什么关心州的发展?
截至 2025 年 5 月,专用于状态的 Geth 节点中当前未压缩的数据库大小约为 340 GiB。在将 gas 限制从 3000 万 gas 单位增加到 3600 万 gas 单位后,每天创建的新状态的中位数大小翻了一番,从约 102 MiB 增加到约 205 MiB。
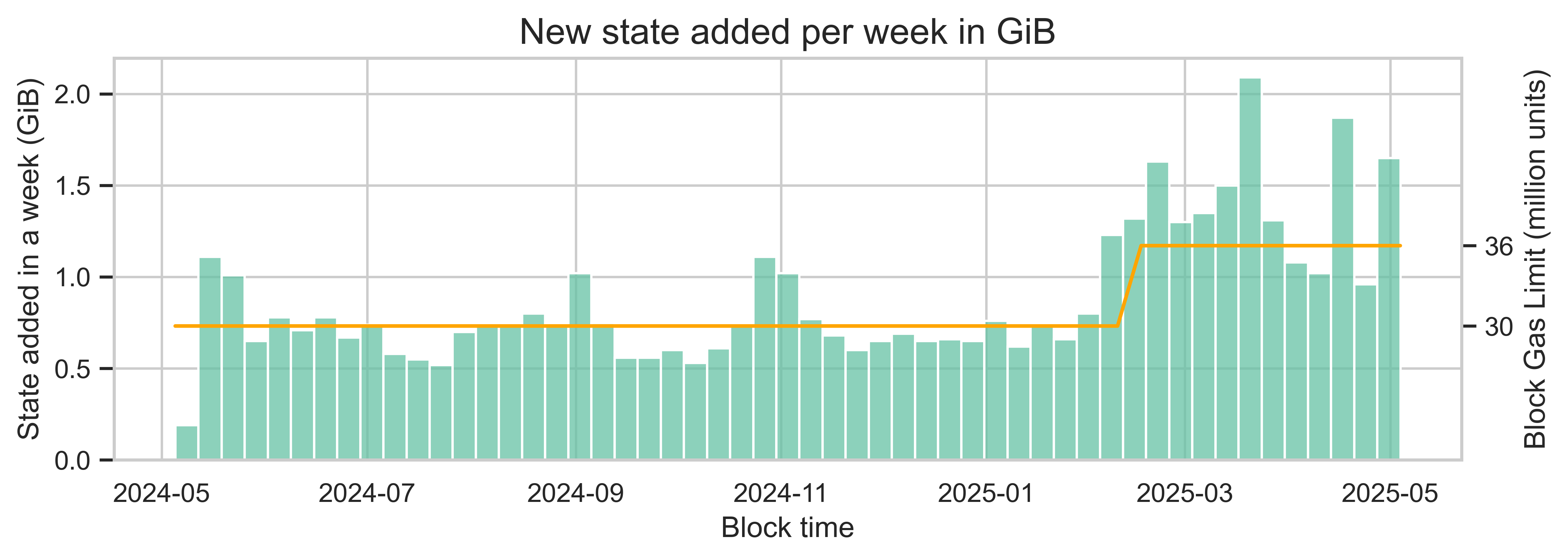
在这个例子中,我们看到的关系并非线性,与预期不符。这可能是由于其他因素影响了用户行为。然而,在其他条件相同的情况下,我们预期随着 gas 限制的增加,新创建的状态数量也会成比例增加。
高州增长率会产生两个负面的后续影响:
- 如果状态增长速度超过磁盘改进和每字节存储容量的减少速度,我们最终会达到这样一个临界点:验证器价格过高,无法满足运行以太坊验证器节点所需的磁盘需求。
- 状态访问操作(例如
SSTORE的性能很大程度上取决于状态的大小,状态越大,这些操作的执行时间就越长。bloatnet项目发现,当状态大小达到 650 GiB 时,状态访问模式会出现关键瓶颈,导致状态访问时间增加 40%,内存消耗呈指数级增长,同步时间也更长。
目前尚不清楚硬件改进和客户端优化将如何影响这些瓶颈;然而,鉴于当前对可扩展性的关注以及预期中 gas 上限的提高,我们需要更仔细地研究这个问题。最重要的是,我们需要就以太坊在中长期内可接受的状态增长水平达成共识。
然而,本报告的重点略有不同:天然气限额预计将如何影响各州的增长,以及天然气重新定价将如何改变其增长轨迹。这一点与即将推出的格拉姆斯登(Glamsterdam)分叉方案提出的EIP-8037尤为相关。
2. 区块限制增加时,州的发展情景:州可以发展到多大?
为了回答这个问题,我们设计了从 2025 年 5 月 1 日到 2027 年年中期间三种不同的天然气限量增加方案:
| 日期 | 保守的 | 根据 | 挑衅的 |
|---|---|---|---|
| 2025-05-01 | 36 | 36 | 36 |
| 2025-07-01 | 45 | 45 | 45 |
| 2025-12-01 | 60 | 60 | 60 |
| 2026-06-01 | 80 | 100 | 150 |
| 2026-12-01 | 150 | 300 | 500 |
| 2027-06-01 | 200 | 400 | 700 |
然后,对于每个调度,我们计算相应的状态增长率,假设每天的状态增长量与 gas 限制成正比,并且基准测量的状态创建率为在 36M gas 限制下每天 205 MiB:
new_state_per_day = 205 MiB * (G / 36M)
由此,我们可以得出每次天然气限价调整日各州每日增长率如下:
| 日期 | 保守估计(百万字节/天) | 基础(MiB/天) | 激进型(MiB/天) |
|---|---|---|---|
| 2025-05-01 | 205 | 205 | 205 |
| 2025-07-01 | 256 | 256 | 256 |
| 2025-12-01 | 342 | 342 | 342 |
| 2026-06-01 | 456 | 569 | 854 |
| 2026-12-01 | 854 | 1708 | 2847 |
| 2027-06-01 | 1139 | 2278 | 3986 |
下图显示了未来两年内三种天然气供应方案的总状态大小(单位:GiB)。
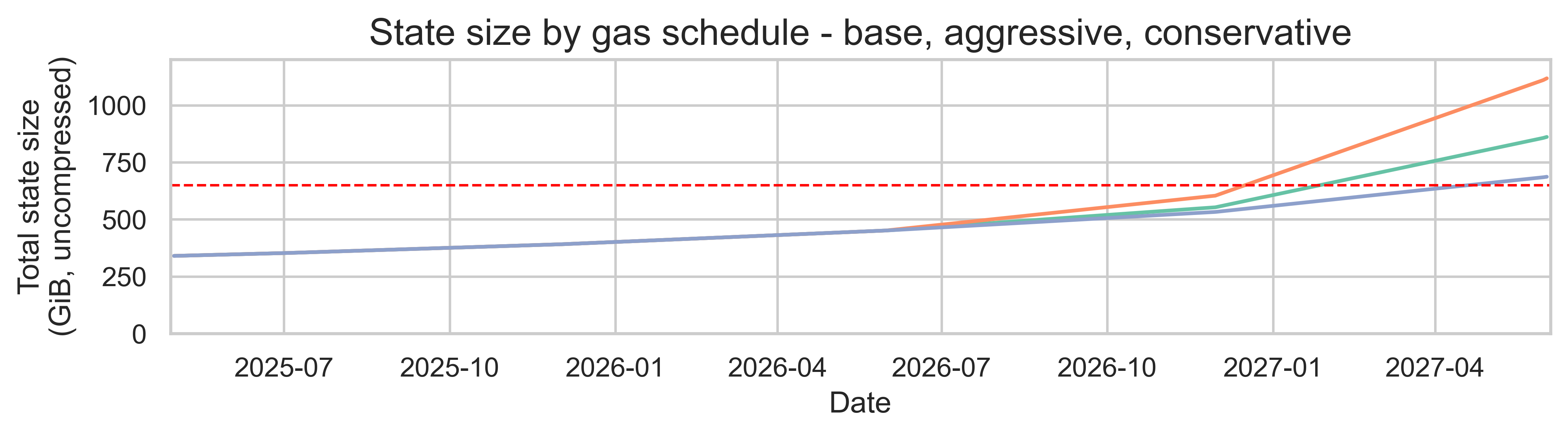
在比例缩放(保持相同 gas 成分)下,增加区块限制会线性增加每日状态创建量(因为我们将测得的 205 MiB/天按 gas 限制比例进行缩放)。由于每日新增状态会累积,因此不同 gas 方案下的总状态大小会在数月和数年内出现差异。到 2027 年年中,保守方案的总状态大小将达到 686 GiB,基础方案为 859 GiB,而激进方案为 1.08 TiB。所有这些值都超过了bloatnet 倡议确定的 650 GiB 临界阈值。
3. 重新定价如何影响州增长和吞吐量?
既然我们已经确定了在价格不变的情况下状态增长的潜在情景,我们就可以分析提高状态创建操作的 Gas 价格如何影响状态增长和可扩展性。
3.1 模型和推导
我们首先定义一个简单的模型,该模型允许我们估算平均每日状态增长量以及区块中可用于突发操作(计算、状态访问和数据)的 gas 量。
模型输入
- G G :阻塞气极限。
- b b :以 gwei 为单位的均衡基本费用b b 。
- g_\text{state} g state : 添加到状态字节的每个新字节的 gas 成本。
- g_\text{burst} g burst :每秒突发资源使用所需的 gas 费用。
- S(p) S ( p ) : 状态创建的需求曲线,以价格p为单位衡量愿意在一个块中添加的净状态字节总数。注意, p是以 gwei 为单位向状态添加一个字节的成本,计算公式为p=b\cdot g_\text{state} p = b ⋅ g state 。
- B(p) B ( p ) : 需求曲线突发资源使用情况,以价格p p为单位衡量愿意在区块中添加的时隙时间(以秒为单位)。在这种情况下, p=b\cdot g_\text{burst} p = b ⋅ g burst 。
模型假设
- 基本费用遵循 EIP-1559 设计,其中区块使用量超过G G的 50% 会导致下一个区块的基本费用增加,而区块使用量低于G G的 50% 会导致下一个区块的基本费用减少。
- 按照目前的设计,区块平均占用 50% 的Gas ,其中 30% 用于状态创建,其余用于突发资源。
- 当 50% 的G G足以满足状态创建和突发资源使用的需求,且价格为p p时,即可达到平均块均衡。
- 两条需求曲线均采用两个独立的等弹性模型进行建模:
这里,我们假设对可处理性的需求是独立的等弹性需求。然而,在实践中,状态创建和突发资源的需求很可能是相关的:状态字节有效价格的变化会影响突发秒数的需求(反之亦然)。采用包含交叉价格弹性的联合多元需求模型可以更好地捕捉资源之间的替代或互补关系,但这会引入额外的参数和识别挑战。
设想
- 气体极限增加n倍,即G = n \, G^0 G = n G 0
- 州天然气成本增加m倍,即g_\text{state} = m \, g_\text{state}^ 0 g state = m g 0状态
我们预计基本费用会下降,直到达到一个新的平衡状态,届时状态资源和突发资源都会得到充分利用。
基础推导
设价格为p时,每个区块的均衡使用量为
- 状态字节: S(p)=S(b g_\text{state}) S ( p ) = S ( b g state )
- 突发秒数: B(p)=B(b g_\text{burst}) B ( p ) = B ( b g burst )
基准费用 b 中每个区块所用的天然气量定义为:
对于该场景,EIP-1559 使b b趋向于值b^* b ∗ ,使得:
在这种新的平衡状态下,我们得到以下每个区块的使用情况:
- S^* = S(b^* \, m\, g_\text{state}^0) S ∗ = S ( b ∗米g 0状态) ,这导致平均每年状态增长2,628,000\cdot S^* 2,628,000 ⋅ S ∗字节。请注意, 2,628,000 2,628,000是每年的数据块数(即每 12 秒一个数据块)。
- B^* = B(b^* g_\text{burst}^0) B ∗ = B ( b ∗ g 0 burst )
每种资源类型的份额如下:
- \text{Share}_\text{state}=\frac{m\,g_\text{state}^0S^*}{0.5\, n\, G_\text{limit}^0} Share state = m g 0状态S ∗ 0.5 n G 0极限
- \text{Share}_\text{burst}=1-\text{Share}_\text{state}突发份额= 1 −状态份额
校准
已知当前G=G^0 G = G 0 ,均衡b=b^0 b = b 0 ,初始 gas 价格g_\text{state}^0 g 0 state和g_\text{burst}^0 g 0 burst ,我们得到:
- g_\text{state}^0 S(b^0 g_\text{state}^0)= 0.3 \cdot 0.5 \cdot G^0 = 0.15\, G^0 g 0 state S ( b 0 g 0 state ) = 0.3 ⋅ 0.5 ⋅ G 0 = 0.15 G 0
- g_\text{burst}^0 B(b^0 g_\text{burst}^0)= 0.7 \cdot 0.5 \cdot G^0 = 0.35\, G^0 g 0 burst B ( b 0 g 0 burst ) = 0.7 ⋅ 0.5 ⋅ G 0 = 0.35 G 0
由此,我们可以将A_s和A_b校准如下:
A_s = S(p)p^{\varepsilon_s} = \frac{0.15\,G^0}{g_\text{state}^0}\,(b^0g_\text{state}^0)^{\varepsilon_s} A s = S ( p ) p ε s = 0.15 G 0 g 0状态( b 0 g 0状态) ε s
A_b = B(p)p^{\varepsilon_b} = \frac{0.35\,G^0}{g_\text{burst}^0}\,(b^0g_\text{burst}^0)^{\varepsilon_b} A b = B ( p ) p ε b = 0.35 G 0 g 0爆发( b 0 g 0爆发) ε b
在这种选择下,对于任意b值,我们得到平衡状态下模块中所用气体的以下公式:
我们还可以根据 gas 限制和当前状态增长率来估算g_\text{burst}^0 g 0 burst 。这里我们假设 gas 限制利用率为 50%,并取平均成本:
对于突发资源,我们将根据最坏情况的区块进行定价,即假设如果区块中充满了突发资源操作直到达到区块限制,则执行时间为 2 秒:
由此,我们可以直接推导出突发资源的基本吞吐量:
情景推导
在这种情况下, G=n\,G^0 G = n G 0 , g_\text{state}=m\,g_\text{state}^0 g state = m g 0状态和g_\text{burst}=g_\text{burst}^0 g burst = g 0 burst ,这使得平衡状态下模块中使用的气体总量为:
此外,在平衡状态下,我们使用了新气体极限的 50%,因此:
我们可以计算该多项式的根来找到均衡基本费用b^* b ∗ 。如果该多项式存在根r \in \mathopen] 0,1\mathclose[ r ∈ ] 0 , 1 [ ,则b^* = b^0 \, r b ∗ = b 0 r .由此,我们可以计算出基本推导中定义的每个区块的使用量和 gas 份额。
以下各节将探讨三种情景的影响:
- 基准(不重新定价): n=2 n = 2 (双倍 gas 限制), m=1 m = 1 (状态 gas 成本不变)
- 双州汽油价格: n=2,m=2 n = 2 , m = 2
- 三态天然气价格: n=2,m=3 n = 2 , m = 3
在所有情况下,我们都假设气体极限加倍( n=2 n = 2 )。
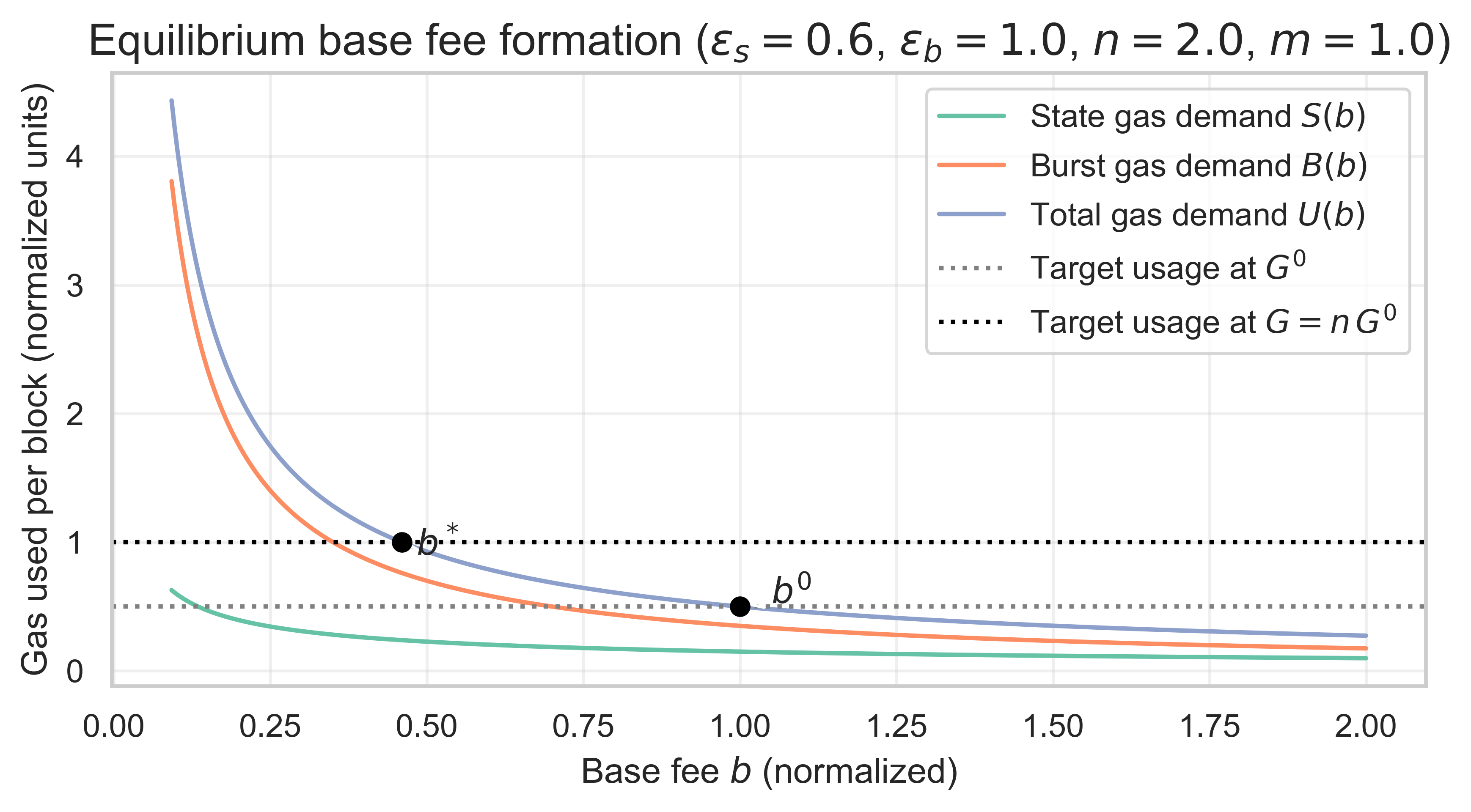
对于每种情景,我们扫描网格(0.1 到 1.5)上的 ε <sub> s </sub>和ε<sub> b </sub> ,并求解b<sup>* </sup> 。利用均衡基准费用b<sup>* </sup> ,我们计算S<sup>* </sup> 、 B<sup>* </sup> 、年度州增长率(单位为 GiB)以及资源天然气份额。为了便于理解,下图展示了基准情景下的新均衡,假设ε<sub> s </sub> = 0.6和ε<sub> b </sub> = 1。
3.2 重新定价对国家创建天然气使用份额的影响
以下图表显示了所有价格弹性组合(\varepsilon_s, \varepsilon_b)下,状态创建操作在均衡块中使用的气体份额( ε s , ε b ) 。
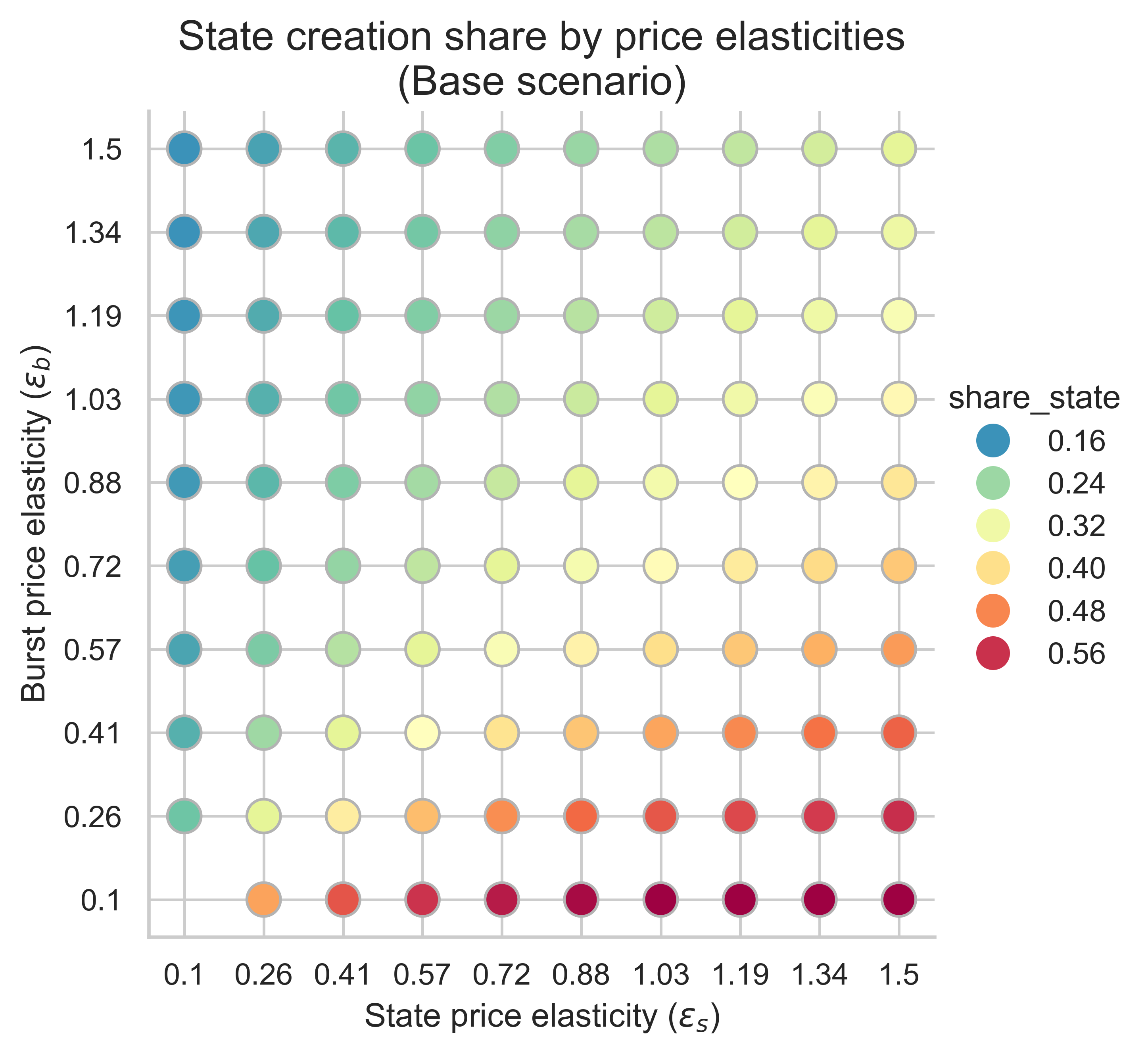
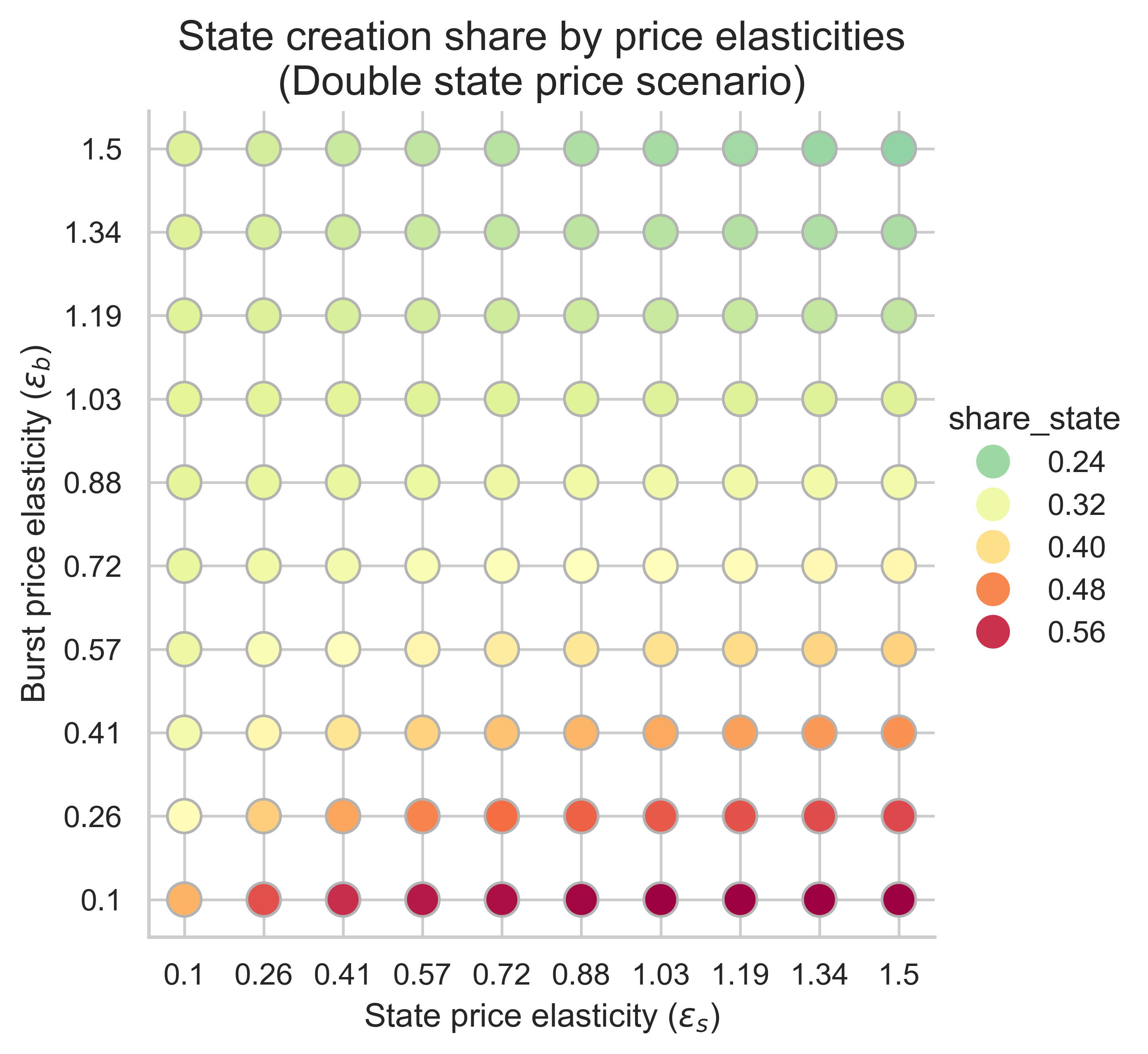
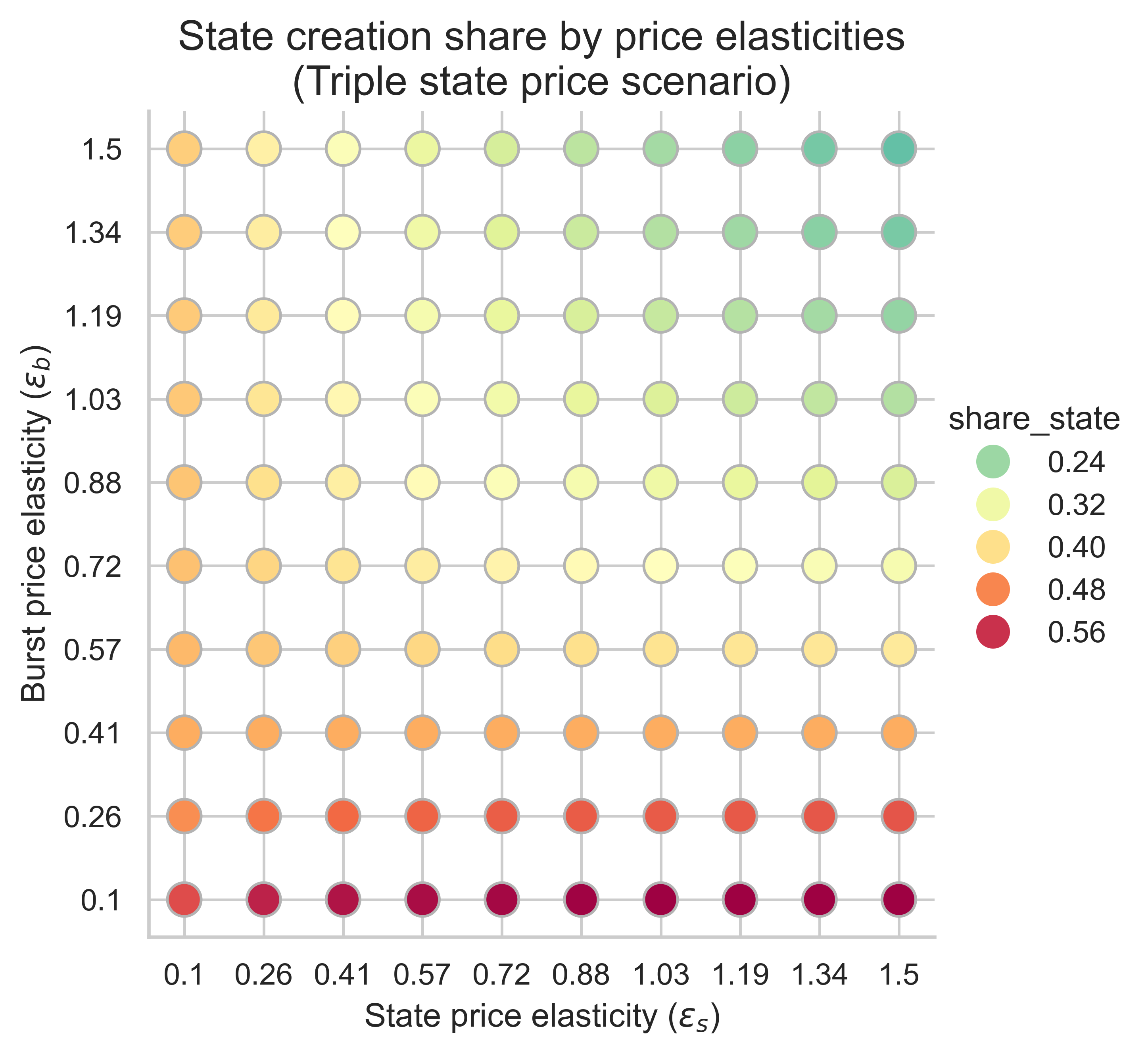
当m = 1 (不重新定价)且n = 2 (双倍gas上限)时,状态创建消耗的区块 gas 比例相对于当前的 30% 有所增加,因为状态创建的需求弹性大于突发资源的需求弹性。因此,如果状态创建对价格变化的适应性强于对突发资源使用量的适应性,那么提高 gas 上限可能会导致更多区块容量用于状态创建,因为更多的状态创建需求会涌入区块以利用更低的基础费用。
增加m m (使状态创建成本更高)会影响状态低弹性机制和突发资源高弹性机制中用于状态创建的区块份额:
- 当状态创建的需求弹性较低时(图表的左侧),我们看到用于状态创建操作的 gas 比例较高, m m越大,比例就越高。
- 相反,当两个需求都具有高弹性时(右上角),效果则相反,与m= 1的情况相比,用于状态创建的模块比例会减少。变化的幅度同样取决于m 。
- 状态创建比例最高的情况出现在突发资源需求弹性较低的时候(图的下半部分)。在这种情况下,增加状态创建成本不会产生任何影响。
总之,提高状态创建的 gas 成本可能会对均衡区块中用于状态创建的份额产生正面或负面的影响。这取决于弹性机制。然而,当基准情景下用于状态创建的区块空间份额已经很高时( m=1 ) ,提高状态创建的 gas 成本并不会显著影响这一份额。换句话说,如果我们处于一种弹性机制下,随着区块限制的增加,用于状态创建的 gas 份额已经很高,那么提高其 gas 价格不会产生显著影响。
3.3 重新定价对年度州增长的影响
以下图表显示了所有价格弹性组合(\varepsilon_s, \varepsilon_b)的年度州增长率( ε (s , ε( b) ) 。这里我们假设平均块是均衡块。该指标对于理解提高状态创建操作成本在缓解状态增长方面的有效性至关重要。
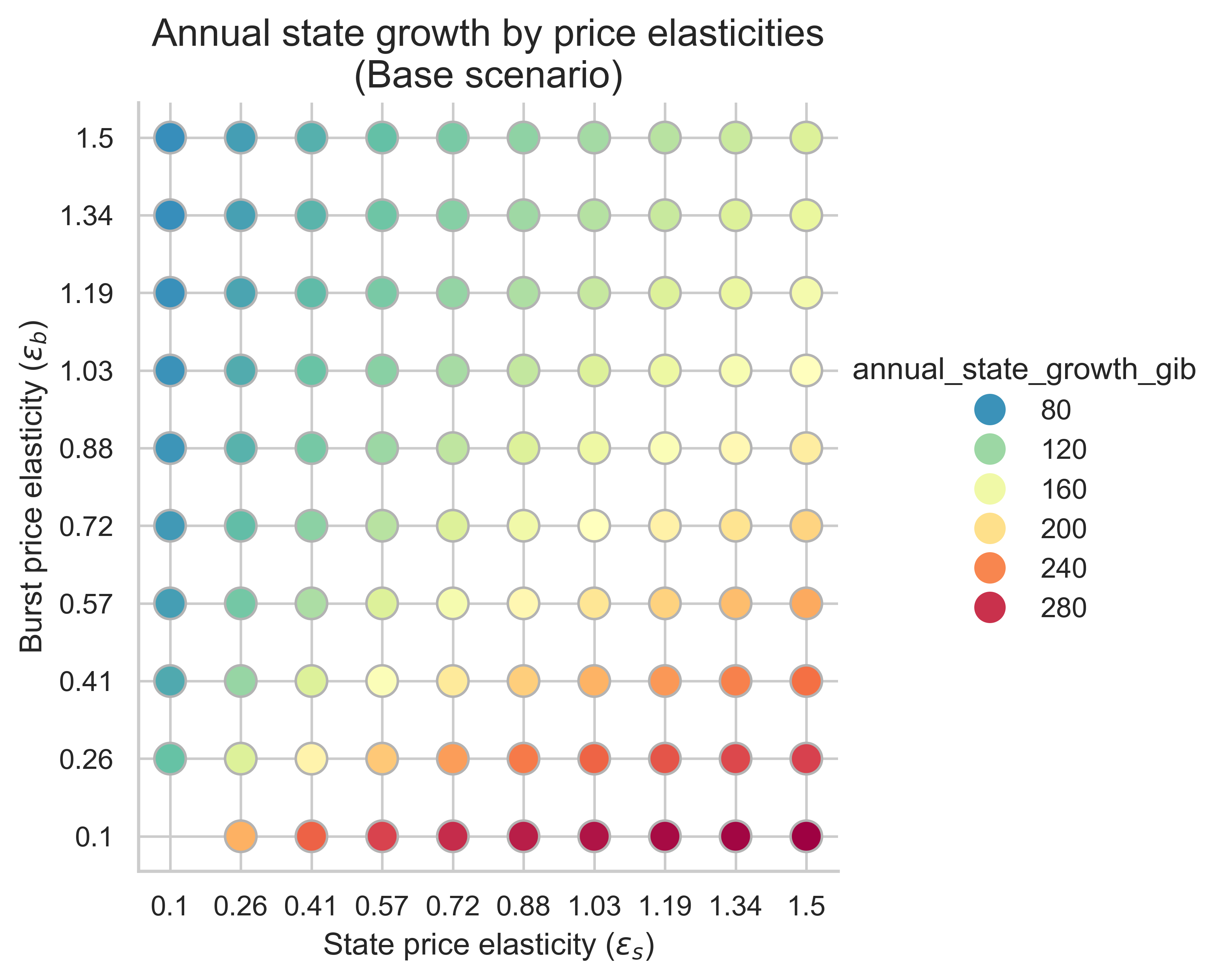
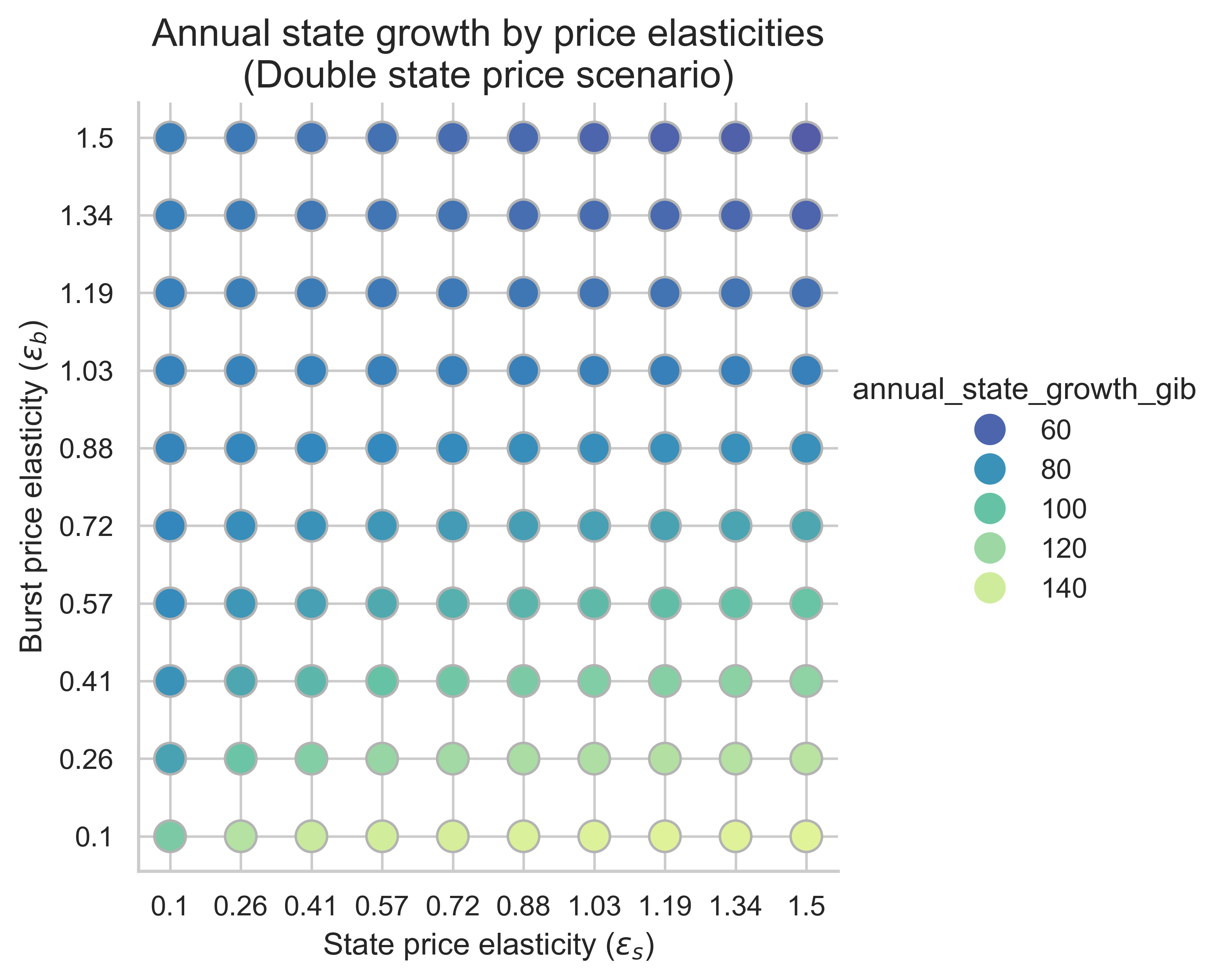
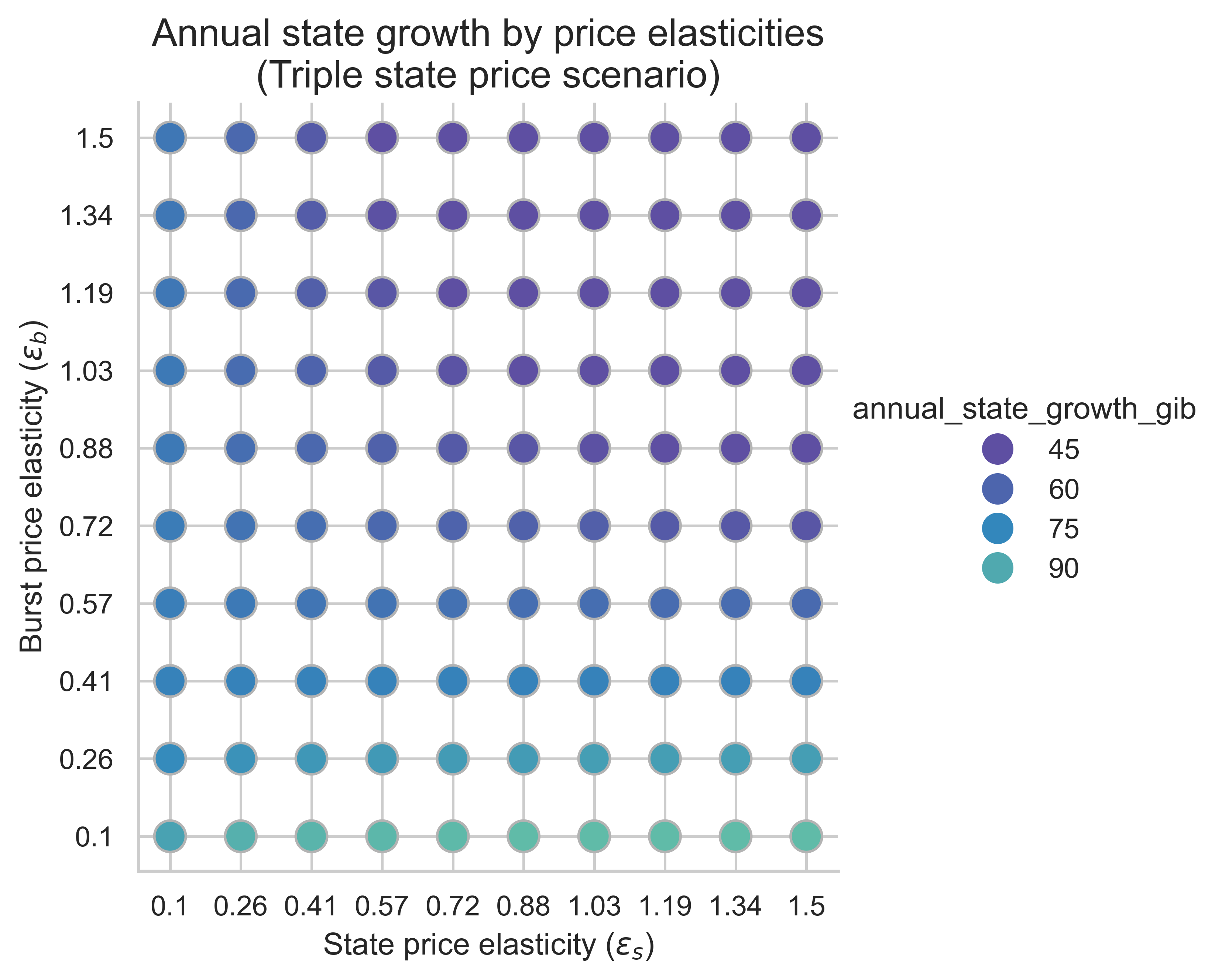
不出所料,与不重新定价的情况相比,提高状态创建操作的成本会降低所有弹性范围内的状态增长率。这表明,提高状态创建的 Gas 成本能够有效抑制各种价格弹性下的状态增长。
增加状态创建的 Gas 成本会产生另一个有趣的效应。我们可以通过绘制每个场景下年度状态增长率与状态需求弹性\varepsilon_s ε s的关系图来观察这一点。每个箱线图的变化是由于突发需求弹性\varepsilon_b ε b造成的。
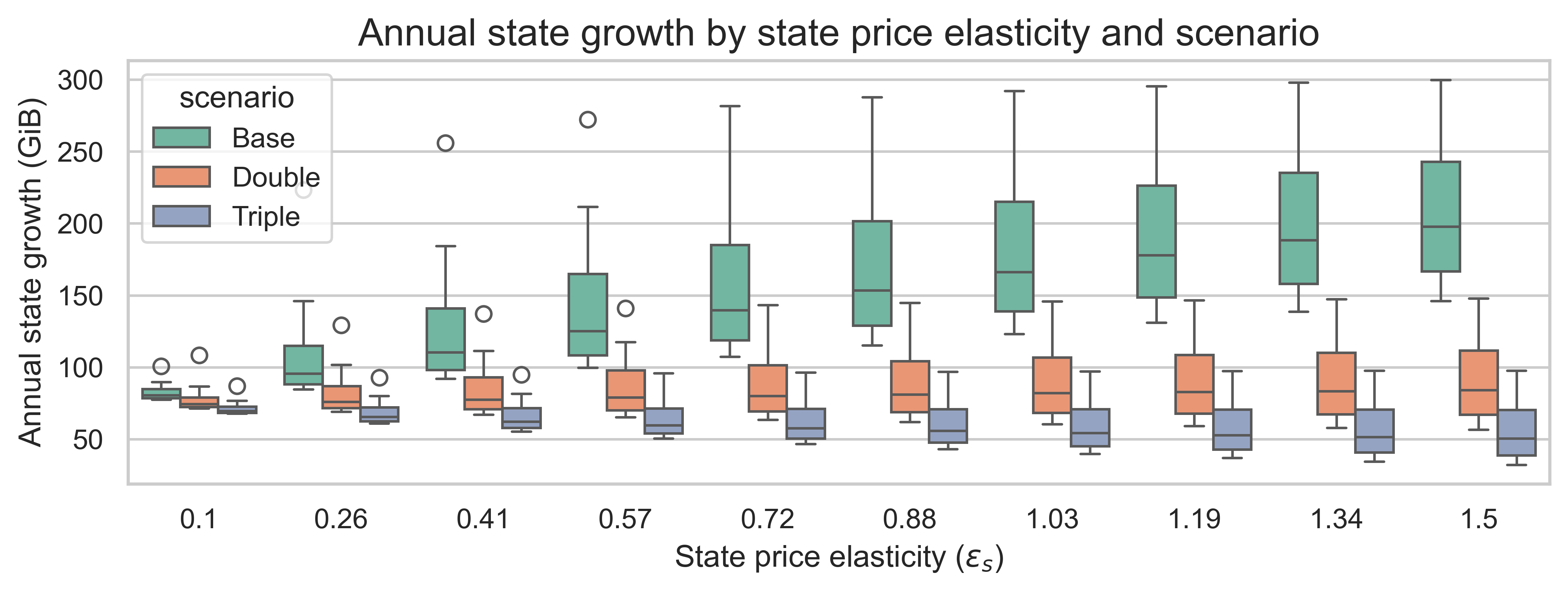
- 无需重新定价:较高的\varepsilon_s \implies ε s ⟹更多州增长
- 重新定价等于区块限制的增加量:更高的\varepsilon_s \implies ε s ⟹州中位数增长率没有变化
- 重新定价高于区块限制的增幅:更高的\varepsilon_s \implies ε s ⟹州增长减少
我们应该注意到,突发资源的需求弹性也会影响状态增长:弹性越低,所有场景下的状态增长率就越高。
3.4 重新定价对突发资源吞吐量的影响
以下图表显示了均衡块中所有价格弹性组合(\varepsilon_s, \varepsilon_b)下突发资源的吞吐量增益( ε s , ε b ) 。增益是在 0.7 秒基准吞吐量的基础上计算的。
该指标对于衡量状态创建成本增加对可扩展性的影响至关重要。如果我们把可用 gas 翻倍,突发资源的吞吐量是否还能至少翻倍?请记住,基准吞吐量为 0.7 秒。
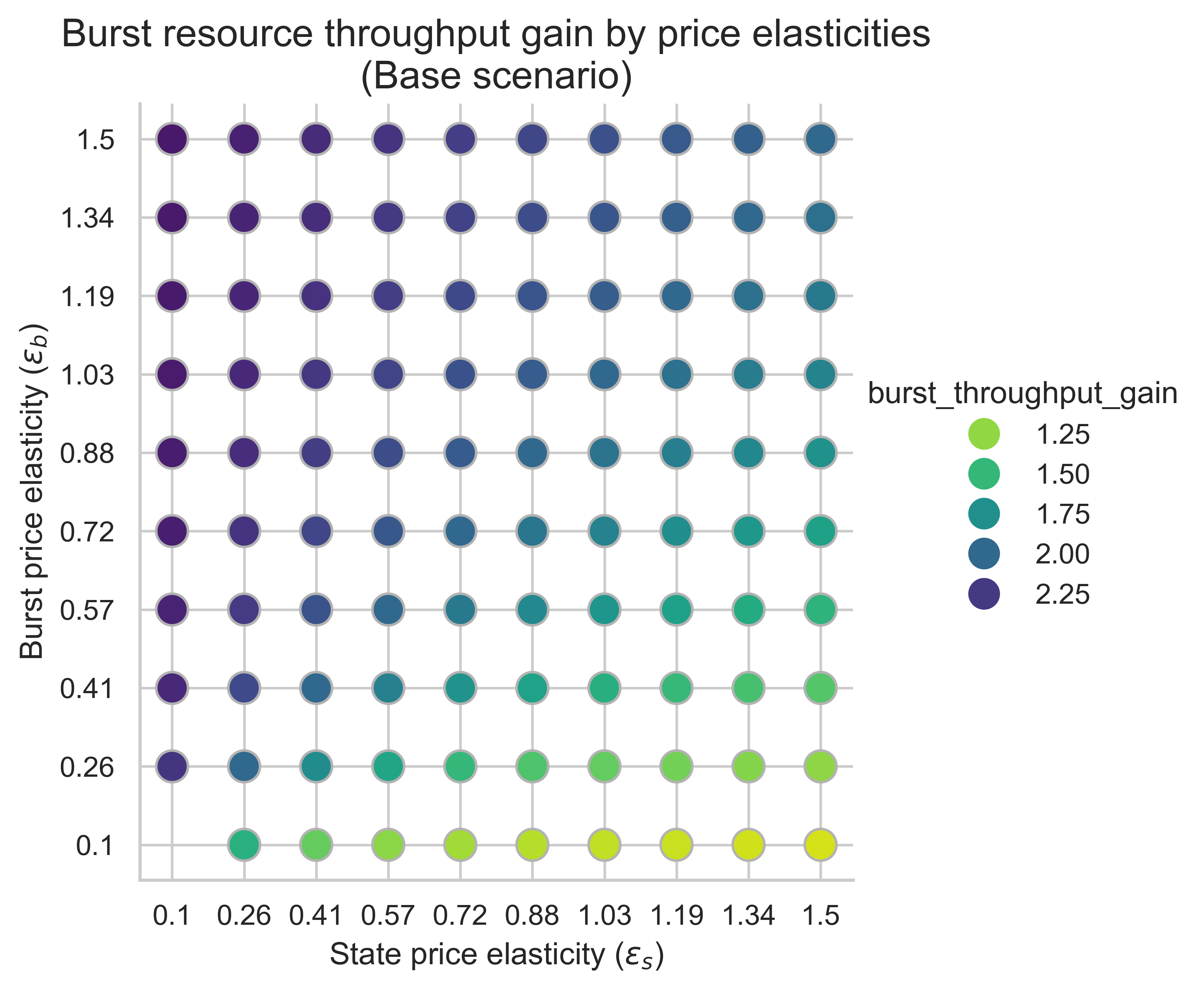
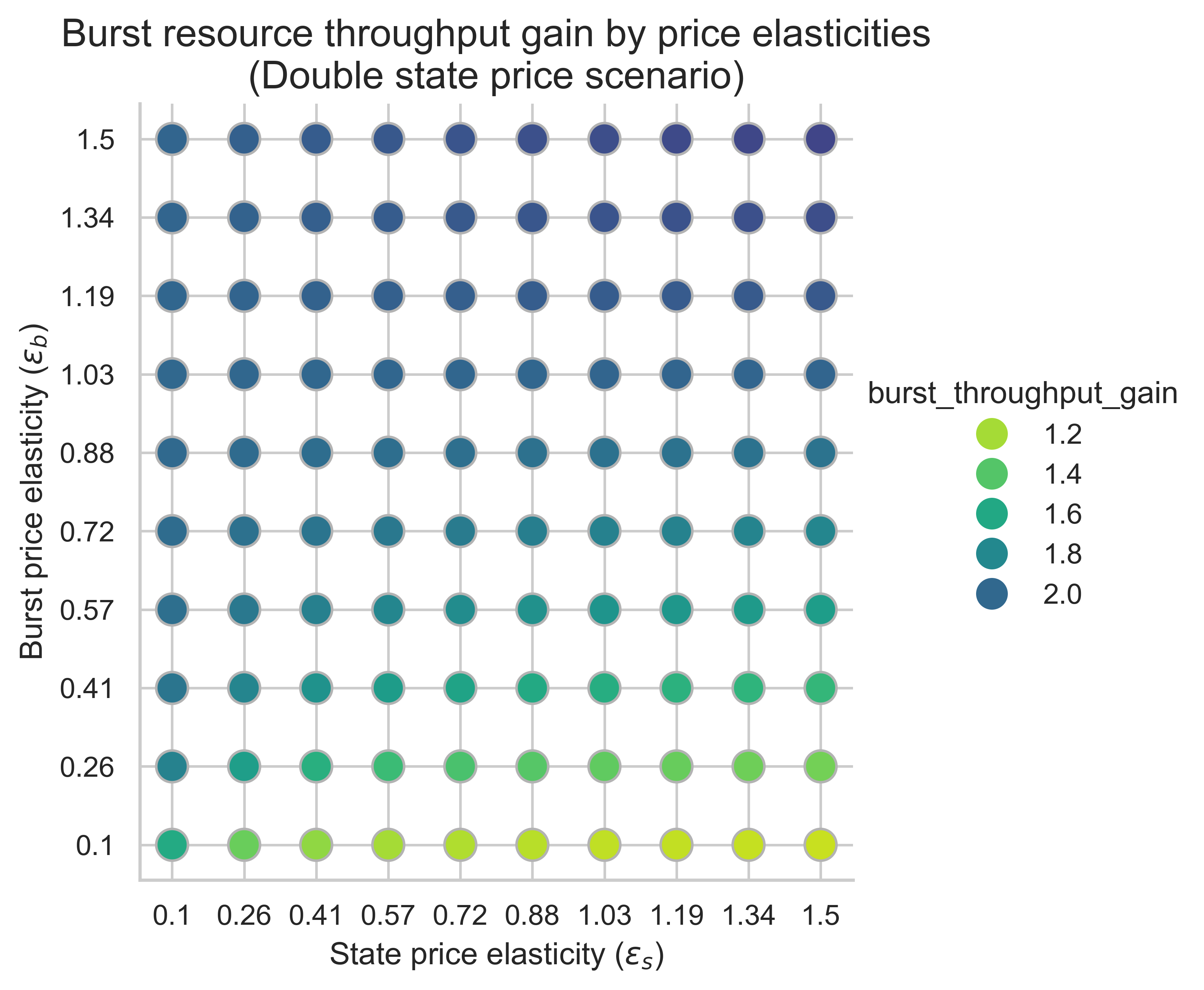
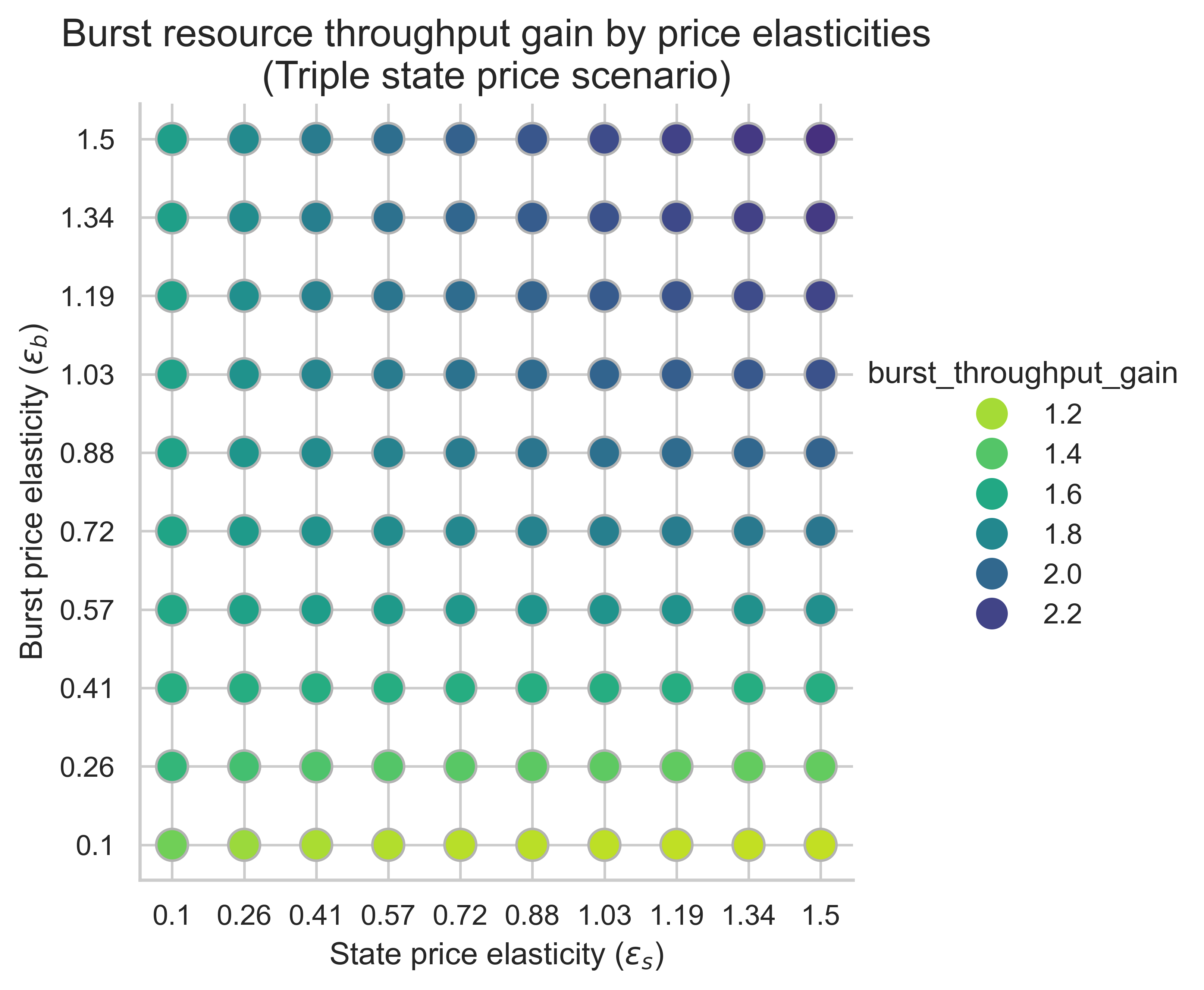
在所有三种情况下,突发吞吐量提升的主要驱动因素是突发侧价格弹性\varepsilon_b ε b 。随着\varepsilon_b ε b 的增加,我们看到相对于 0.7 秒基准线,增益越来越大:
- 当突发需求具有足够的价格弹性(图表的上半部分)时,产能翻倍意味着突发吞吐量翻倍(或略微增加)。
- 当突发需求缺乏弹性时(图表底部),产能翻倍所对应的突发吞吐量不到翻倍。
相比之下,水平方向随状态弹性ε<sub> s </sub>的变化更为复杂。当m = 1 时,随着ε <sub> s </sub>增大,增益略有下降。而当m = 2或m = 3时,突发资源吞吐量增益在两个价格弹性都较高时达到最高。
在下图中,我们可以更清楚地看到提高状态创建成本对吞吐量的影响。每个箱线图的变化是由于状态需求弹性\varepsilon_s ε s引起的。
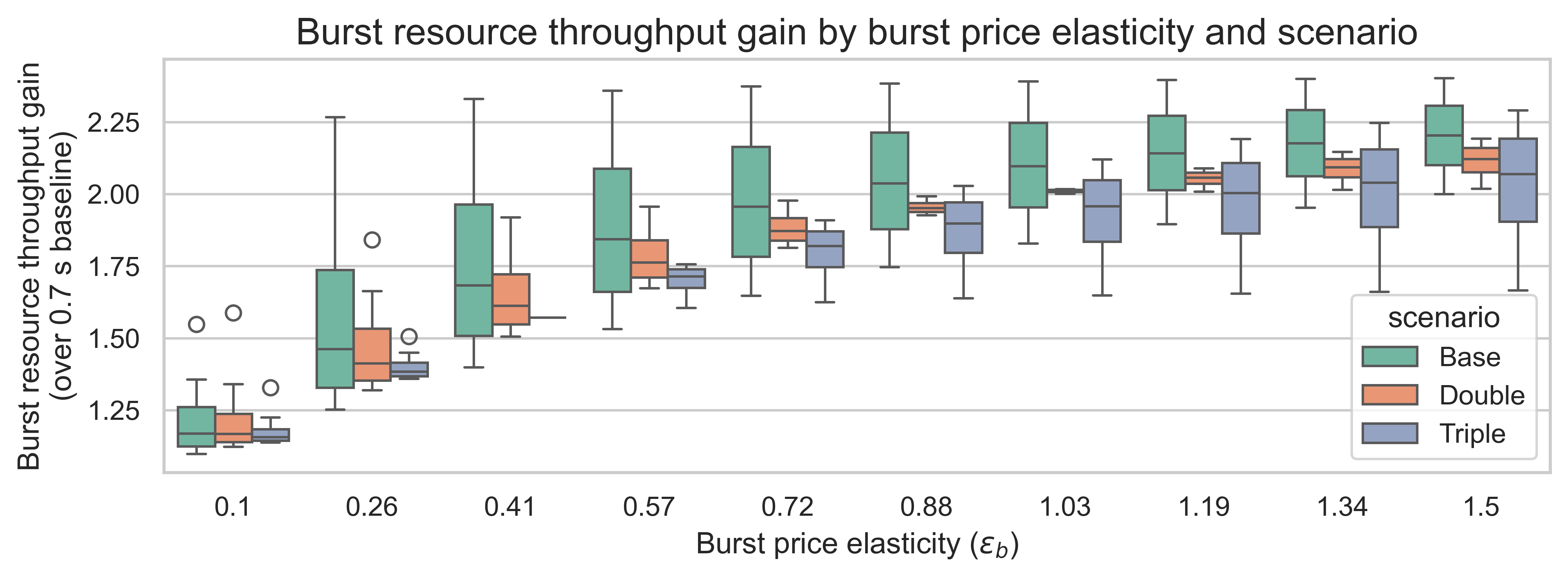
一般来说,成本上升会略微降低吞吐量的提升。然而,与突发资源需求弹性的影响相比,这种影响微乎其微。如果处于高ε<sub> b</sub> ε <sub> b </sub>状态,那么增加状态创建对吞吐量的影响小于25%。
3.5 均衡费用
我们要分析的最后一个指标是均衡基本费用。我们预期该费用会低于基准值b^0=1 b 0 = 1。然而,在不同的弹性机制和重新定价的情况下,费用会降低多少呢?下图展示了三种重新定价情景下的均衡基本费用以及突发需求弹性。每个箱线图的变化是由状态需求弹性\varepsilon_s ε s引起的。
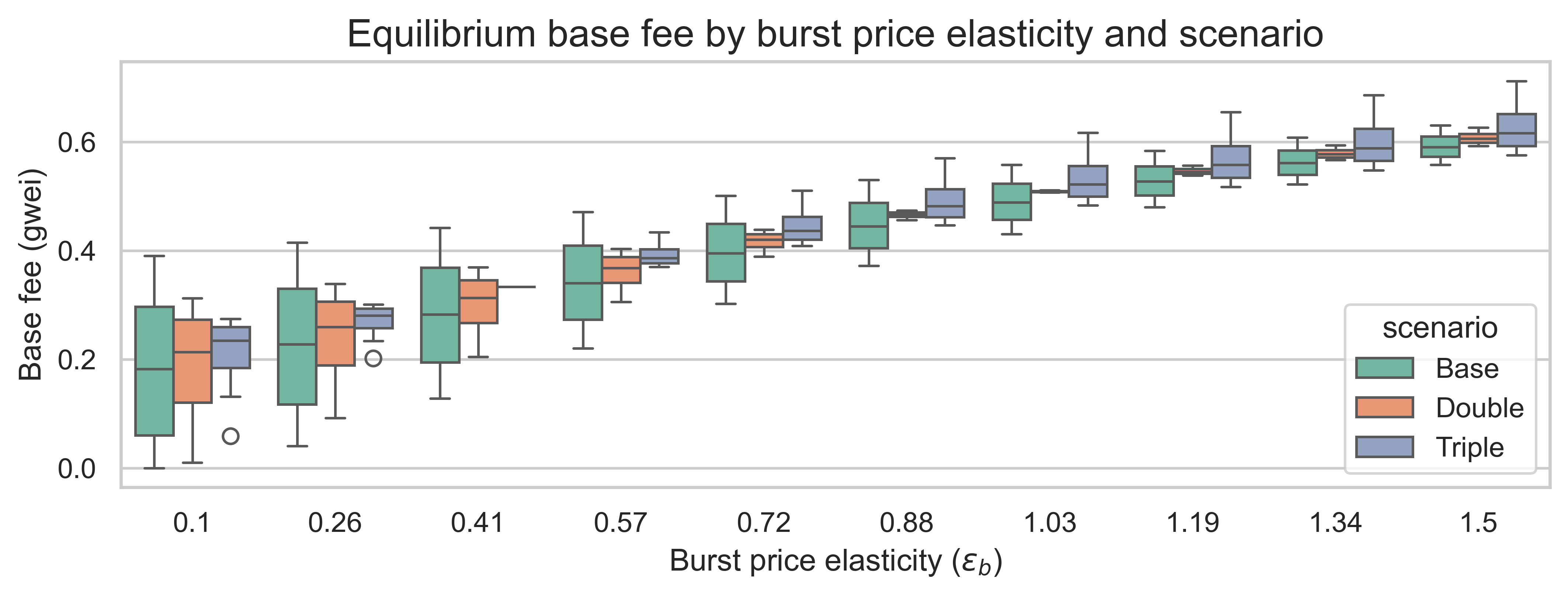
在所有三种定价情景下,均衡基础费用均随突发需求价格弹性的增加而增加:从突发需求弹性很低( ε<sub> b </sub> ≈0.1 )到弹性很高( ε<sub> b </sub> ≈1.5 ) ,基础费用的中位数大约会增加两倍。当弹性较高时,会有更多需求来填充可用燃料,从而导致更高的基础费用。
那么状态需求弹性如何呢?下图显示了三种重新定价方案的均衡基本费用和状态需求弹性。每个箱线图的变化是由于突发需求弹性\varepsilon_b ε b造成的。
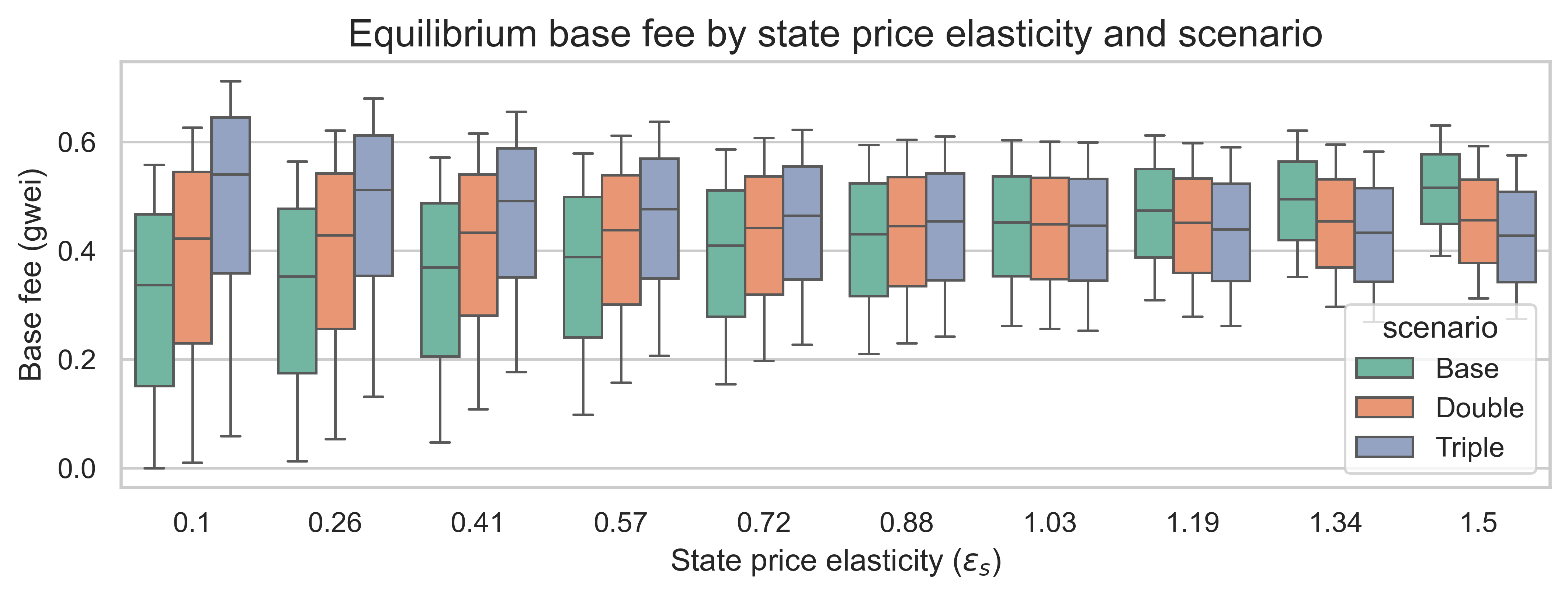
有趣的是,我们并未观察到基本费用与各州需求之间存在同样的线性关系,基本费用的中位数似乎不受各州需求弹性的影响,始终保持在相似的范围内。然而,弹性机制确实会对不同情景下的排序产生影响:
- 当州需求缺乏弹性时(图表左侧),较高的州价格会导致更高的均衡费用。在这种情况下,提高州的价格对需求的影响不大,因此,相同的州需求需要消耗更多的天然气。
- 当状态需求弹性较大时(图表右侧),较高的状态价格会导致较低的均衡费用。在这种情况下,状态创建需求对状态成本的增加反应更为强烈,从而降低了基本费用。
4. 讨论和后续步骤
首先,在我们简化的模型下,提高状态创建操作的成本可以有效抑制所有价格弹性下的状态增长。因为gas不足以支撑状态像基础定价方案下那样大幅增长。然而,这仍然会导致突发资源吞吐量略微下降。突发资源的需求弹性会加剧这种影响——需求弹性越大,所有定价方案下的吞吐量提升就越高。如果状态创建需求缺乏弹性,那么提高状态创建成本预计会导致基础费用高于状态不重新定价的情况。
一个自然而然的问题是,实际系统在(ε<sub>s</sub>, ε<sub>b</sub>) ( ε <sub>s</sub> , ε<sub> b </sub> )网格中的位置。我们的初步实证分析表明,短期内状态创建的需求弹性适中:以美元计价的基础费用上涨 1%,在接下来的几天里,每单位 gas 创建的新状态数量仅下降约 0.6%。从等弹性角度来看,这表明短期内状态创建的总工作负载约为 ε<sub> s </sub> ≈ 0.6 。这与直觉相符,即许多状态密集型操作(例如开仓、创建合约、铸造代币、将数据提交到 Rollup 等)是由持续时间更长的经济决策和协议级策略驱动的,这些决策和策略不会立即根据价格变化进行调整。我们还应该补充一点,像 XEN 这样的垃圾合约预计会造成价格下限,因为每当状态创建的总成本低于某个阈值时,机器人就会用大量状态交易淹没网络,从而增加未来区块的基本费用。
对于突发资源,我们目前还没有可比的估计,但有理由预期其弹性会更高,至少在大部分工作负载中是如此。许多以突发为主的活动(套利、清算、MEV 搜索、对延迟敏感的交易)都受到明确的费用限制,并且可以迅速减少。








