EIP-8037 的双资源计量气体方程

01-14

本文为机器翻译

展示原文

感谢在最近的会议中参与讨论这些话题的各位与会者： Maria 、 Ansgar 、 Vitalik 、 Francesco 、 Caspar 、 Julian以及其他许多人。

1. 概述

EIP-8037统一并提高了状态创建的 gas 费用。人们担心gas 费用的增加可能会阻碍扩展性，因为用户在状态创建上花费的 gas 限额比例会更高，从而挤占常规 gas 的使用。因此，研究人员一直在研究如何将状态创建 gas 的限额从所有其他操作的目标和限制中分离出来，为状态创建设置单独的目标和限制。如果重新定价后，状态创建 gas 的占比从 30% 提高到 50%，那么将状态创建独立出来将使所有其他操作的扩展性提升约 100%，这是一个非常诱人的方案。

针对此问题，已提出三种解决方案。除了常规的重新定价之外，以太坊还可以采用EIP-8011中提出的 gas 计量机制。gas 价格可以设置为随 gas 上限动态变化，本文提出了一种可能的规范，EIP-8037 的最新版本也采用了类似的规范。另一种方案是采用计量状态创建，以自适应 gas 成本来控制特定状态的增长，如EIP-8075中所述。

本文分析了一个具体问题：当使用两种不同的资源（常规 gas 和状态创建 gas）时，每个区块的基础费用应该如何更新。本文的经验教训对 EIP-8011 和 EIP-8075 都适用，但对 EIP-8011 尤为重要，因为 EIP-8011 没有目标机制来将两种资源的消耗量控制在一定的相对水平。

首先，本文可视化了现有方法，例如应用max和average函数。然后，提出欧几里得范数作为一种可行的折衷方案。此外，本文还探讨了非对称方法。计量气体方程的非线性程度越高，其非对称性就越强，从而可以最大限度地提高规模。最后，本文概述了最简单的改进：多维气体核算。在本文中，计量气体G G 、常规气体G 1 和状态生成气体G 2 均表示为常规气体极限的分数。

2. EIP-8011 的最大功能

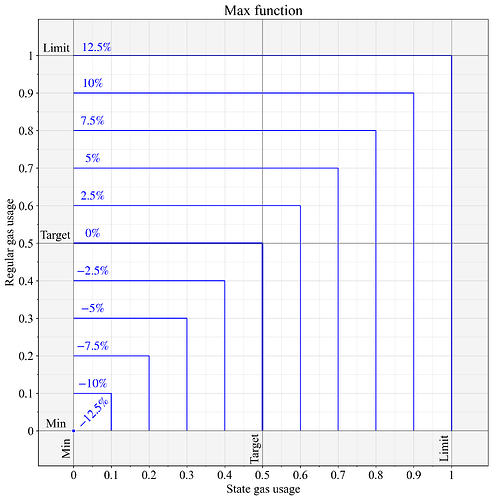
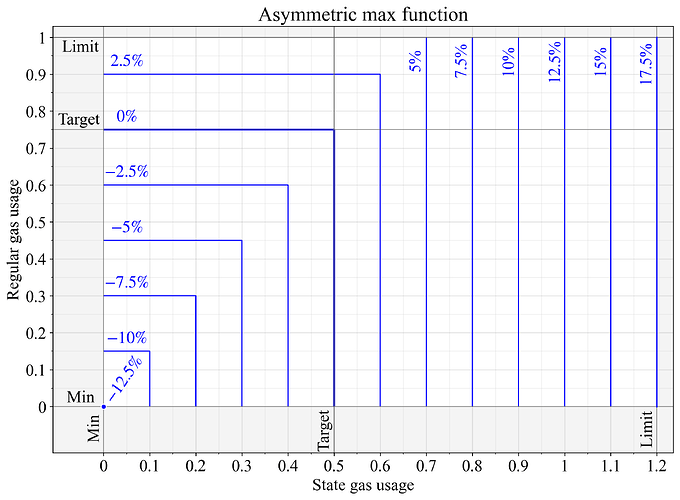
EIP-8011计算计量天然气量G ，并将其输入EIP-1559基本费用更新公式，计算方法为： G为所有独立资源所用天然气量的max 。图 1 展示了计算结果。

一个值得关注的问题是扩展性提升可能不理想。如果某个资源消耗的 gas 量远高于其他资源，由于其基础费用相对于需求量较高，其他资源的 gas 使用率可能会远低于均衡状态下的目标值。需求量较高的资源则始终保持在 50% 左右的目标值。对于计算等突发性受限的资源，理想情况下应该尽可能接近其极限值，否则大多数区块中可用的处理能力都会被闲置。

图 1 2548×2586 199 KB

图 1.应用max函数计算两个独立计量资源计量天然气时的基本费用变化。根据 EIP-1559 规范，价格变化 0% 表示计量资源的计量量为G=0.5， G = 0.5 ；价格变化 12.5% 表示计量量为G=1， G = 1 ； -12.5 %表示计量量为G=0， G = 0。

需要注意的是， max函数的非线性特性会导致长期消耗量低于目标值。即使两种资源的长期消耗量达到平衡，在单个区块层面也未必总是平衡的。因此，价格的设定仅是为了维持利用率较高的资源的目标利用率。例如，如果某些区块的利用率为(0.5 , 0.3 ) ，而其他区块的利用率为(0.3, 0.5)，则长期平均利用率可能仅在( 0.4 , 0.4 )左右。

此外，需要注意的是，两种资源的指定天然气价格可能无法确保它们都达到指定的“目标”消耗量。这既有利也有弊，可以通过计量过程中的预处理步骤进行调整，如第7节所述。

3. EIP-8075 的平均函数

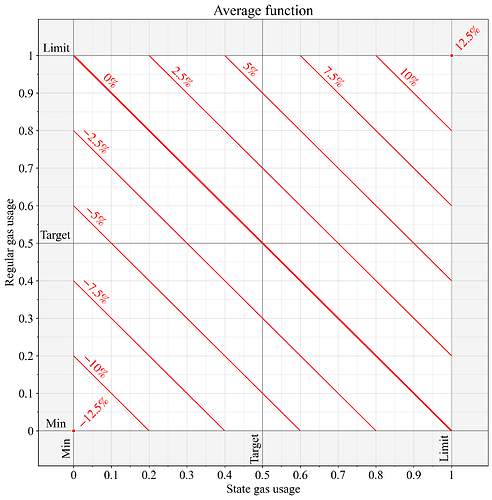
图 2 展示了计量气体G 1 和G2 的average ，即两种独立资源所用气体量的平均值。这是EIP-8075的方法（除了其单独的目标设定步骤）。采用这种计量方法，如果两种资源在平衡状态下的利用率不同，则其中一种资源的利用率会被推高至 50% 以上，另一种资源的利用率则会被推低至 50% 以下。具体来说，由于系统在(G 1 + G 2 ) /2=0.5时达到平衡，因此 G 1 + G 2 = 1 。假设利用率的相对差异保持不变，与max函数相比，这种方法能更好地保持尺度不变，因为总消耗气体量（以归一化单位计）始终为 1。

另一个好处是，与现在一样，这两种资源始终会影响基础费用。之所以采用动态定价拍卖，首先是为了确定每个区块的固定价格，同时该价格可以根据需要进行调整，从而将突发性资源（例如常规 gas）的消耗控制在限值内，并将长期性资源（例如状态增长）的消耗控制在目标水平。为了使状态增长保持在接近某个特定水平，如果一个区块消耗了目标水平的常规 gas 和状态创建 gas，其基础费用与仅消耗目标水平的常规 gas 而未消耗状态创建 gas 时的基础费用有所不同，这似乎是有益的。

图 2 2548×2586 396 KB

图 2.应用average函数计算两个独立计量资源计量天然气时的基本费用变化。根据 EIP-1559 规范，价格变化 0% 表示计量资源的计量量为G=0.5， G = 0.5 ；价格变化 12.5% 表示计量量为G=1， G = 1 ； -12.5 %表示计量量为G=0， G = 0。

如果将此方法应用于 EIP-8011，则需要注意一个问题：长期来看，单个资源的使用量可能会接近其极限。当然，如果 EIP-8011 中使用两个以上的资源，那么其中一个资源可能会完全达到其极限。而 EIP-8075 同样使用average函数，因此不存在两个资源使用量受限的问题，因为状态创建 gas 成本会迅速调整，使两个资源的利用率都恢复到 50% 的平衡状态。

4. 介于`max`和`average`之间的解

max和average函数关注点不同，可以通过将结果置于两者之间来解决。这样既能更好地保持可扩展性，又能防止在分布不平衡的情况下，资源长期接近其极限。

4.1 `max`和`average`的加权组合

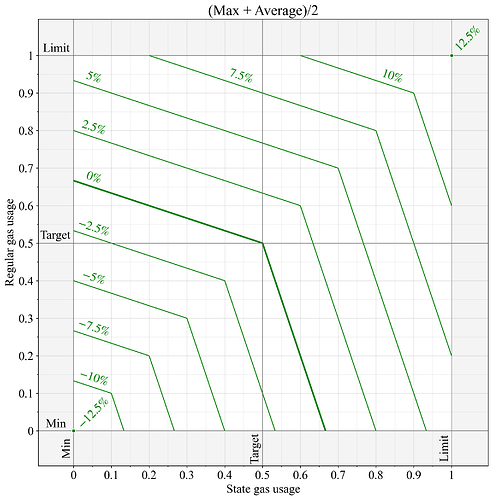
一个简单的解决方案是对两种资源G_1 G 1和G_2 G 2的已用 gas 进行加权平均，即max和average的加权平均值：

G = (1-w) \max(G_1, G_2) + w(G_1 + G_2)/2。

G = ( 1 − w ) max ( G 1 , G 2 ) + w ( G 1 + G 2 ) / 2.

w的两个可能取值是 1/2 和 2/3。图 3 显示了w=1/ 2时的结果，此时完整的方程变为：

G = \frac{\max(G_1, G_2) + (G_1 + G_2)/2}{2}.

G = max ( G1 , G2 ) + ( G1 + G2 ) / 2 。

图 3 2548×2586 461 KB

图 3.应用max和average函数的加权组合 ( w=1/ 2 )计算两个独立计量资源的计量天然气时，基本费用的变化。根据EIP-1559规范，价格变化 0% 表示计量资源的计量值为G=0.5，12.5 % 的价格变化由G = 1产生， -12.5 %则表示G = 0 。

4.2 欧几里得范数

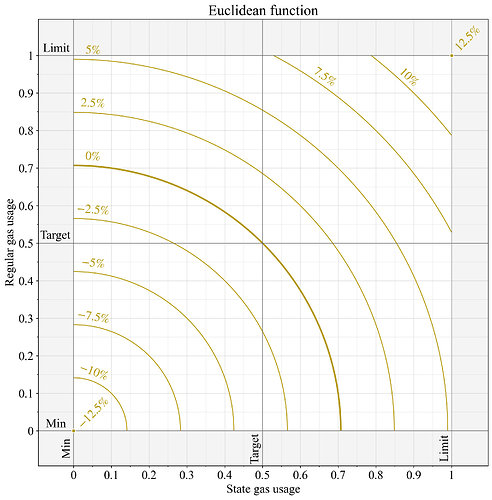
更精细的解决方案是采用欧几里得范数（L2 范数）：

G = \sqrt{\frac{G_1^2+G_2^2}{2}}.

G = √G21 + G222 。

这样就形成了一个平滑的表面（四分之一圆），其中每种资源对计量天然气的边际影响与其当前使用量成正比：

\frac{\partial G / \partial G_1}{\partial G / \partial G_2} = \frac{G_1}{G_2}.

∂G / ∂G 1 ∂G / ∂G 2 = G1 G2 。

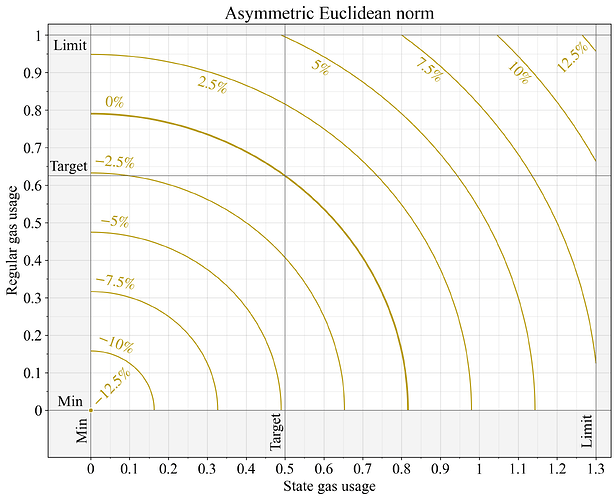
如果当前使用量满足G_1 = 2G_2， G_1 = 2G_2 ，那么额外增加一个单位的常规气体，计量气体的增加量大约是额外增加一个单位的状态生成气体的两倍。因此，该机制对运行量远高于其目标值的特定资源最为敏感，同时始终会受到两种资源消耗量变化的影响。另一个有趣的特性是，当欧几里得范数在接近目标交点运行时，在区块级别上产生的变异阻力非常小。欧几里得范数还具有直观的几何特性，它将计量气体量衡量为到原点的距离。图 4 展示了这一函数。

图 4 2548×2586 454 KB

图 4.应用欧几里得范数计算两个独立计量资源计量天然气时的基本费用变化。根据 EIP-1559 规范，价格变化 0% 表示计量资源的计量值为G=0.5， G = 0.5 ；价格变化 12.5% 表示计量值为G=1， G = 1 ； -12.5 %表示计量值为G=0， G = 0。

从概念上讲， max 、 average和欧氏范数都可以用以下方程式表示。

G = \left(\frac{G_1^p+G_2^p}{2}\right)^{1/p}.

G = ( G p 1 + G p 2 2 ) 1 / p 。

对于平均函数， p=1， p = 1 ；对于欧几里得范数， p=2， p = 2 ；对于最大值函数，p趋于无穷大。

4.3 所有函数的联合图

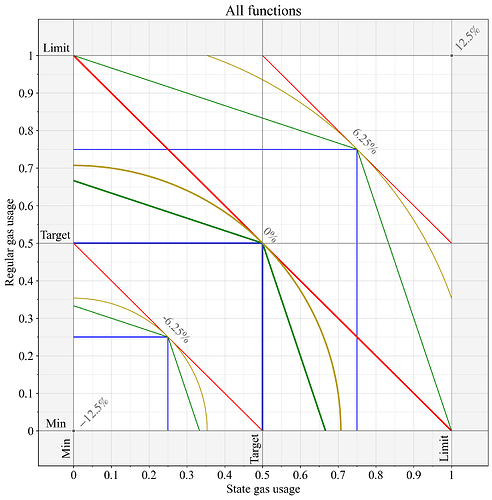
图 5 将图 1-4 中的结果汇总在一起，以便于比较。所有计量气体方程在两种资源均等使用时均得出相同的结果，但在应对资源利用不平衡的情况时则有所不同。

图 5 2548×2586 434 KB

图 5.图 1-4 的基本费用变化在同一张图中呈现。

5. 不对称的目标/极限比率

5.1 动机

非对称的目标/限制比率也是可行的。由于状态增长不受突发限制，因此相对于目标而言，更高的限制可能是有益的。相反，由于常规 gas 受突发限制，理想情况下，其目标和长期平均消耗量应该更接近其限制，就像现在的 blobs 一样。如前所述，在average函数下，如果目标超过限制的一半，而另一种资源未使用，则可能导致其中一种资源完全达到其限制。因此，在计算平均值时，不应提高目标/限制比率，实际上降低该比率可能更可取。

对于其他函数，可以提高突发约束资源的目标/限制比率。这样做的一个动机是，一个资源的利用率高于目标值会降低另一个资源的均衡利用率。目标利用率只是max函数的一个上限——如果一个资源的利用率高于预期，则在均衡状态下，一个资源的实际利用率可能接近于零。此外，如第 2 节所述，区块级别的不均衡利用也会降低均衡利用率。因此，如果两个资源的需求量相等， max函数会认为两个资源的利用率都低于目标值。

5.2 非对称最大值

图 6 中的非对称max函数显示了规则气体目标位于中点上方 1/4 处（极限的 3/4 处），这是通过应用预处理G'_1 = \frac{2}{3}G_1 G ′ 1 = 2 3实现的。G1 。此预处理使得G1 = 3 / 4重置为(3/4)×(2/3)=1/ 2，即在应用max函数之前， ( 3/4 ) × ( 2/3 ) = 1 / 2 。由于此资源不受突发限制，状态gas的上限提高了20%。

图 6 2548×1873 206 KB

图 6.在非对称max函数下的基本费用变化，该函数将常规气体的目标设定为其限制的 3/4，并将状态气体的限制扩大 20%。

5.3 非对称欧几里得范数

在图 7 所示的非对称欧几里得范数下，常规气体目标位于中点上方 1/8 处（即T_1=5/ 8处）。应用线性预处理步骤，使得常规气体和状态气体各一个边际单位在目标交点(T_1,T_2 )处的影响相等。考虑预处理后的欧几里得计量方程：

G = \sqrt{\frac{(c_1G_1)^2+(c_2G_2)^2}{2}}.

G = √ ( c₁G₁ ) ² + ( c₂G₂ ) ² 。

目标点处的边际影响相等意味着∂G/∂G_1 = ∂G / ∂G_2 ∂G / ∂G_1 = ∂G / ∂G_2在( T_1 , T_2 )处成立，简化后为

c_1^2T_1 = c_2^2T_2\qquad\Rightarrow\qquad\frac{c_1}{c_2}=\sqrt{\frac{T_2}{T_1}}.

c 2 1 T 1 = c 2 2 T 2 ⇒ c1 c2 = √T2T1 。

c_1和c_2的值被设定为满足G(T_1,T_2)= T_2 ，因为T_2保持不变，为1/2 。这是在以下情况下实现的：

c_2 = \sqrt{\frac{2T_2}{T_1+T_2}}, \qquad c_1 = \sqrt{\frac{T_2}{T_1}} \sqrt{\frac{2T_2}{T_1+T_2}}.

c 2 = √ 2 T 2 T 1 + T 2 ， c 1 = √ T 2 T 1 √2T2T1 + T2 。

由于状态气体不受突发限制，因此其上限进一步提高了 30%。

图 7 2548×2066 433 KB

图 7.在非对称欧几里得范数下的基本费用变化，其中普通天然气的目标值设定为其极限值的 5/8，并将国有天然气的极限值扩大 30%。对测量的天然气值进行预处理，确保在目标交点(T_1,T_2) 处，一个边际单位的普通天然气和国有天然气具有相同的影响。 ( T1 , T2 ) 。

6. 多维气体核算

为了保持（部分）可扩展性，最简单的机制是沿用当前的 EIP-1559 机制，但在计算区块累计 gas 使用量时，略微减少每个状态 gas 单位的计算。用户仍然需要支付状态 gas 的全价。因此，发送方支付的gas_used计算方式与正常情况相同： gas_used = regular_gas_used + state_gas_used 。但是，在计算区块的cumulative_gas_used时，会应用一个DISCOUNT_FACTOR （例如， DISCOUNT_FACTOR = 2 ），该折扣因子将计入区块的 gas 限制。


 cumulative_gas_used = regular_gas_used + state_gas_used // DISCOUNT_FACTOR

因此，该协议无需分别聚合两种资源来应用计量气体方程，因为它并不试图维护不同的限制。当然，这也不利于扩展性，因为在平衡状态下，状态气体仍然会（在一定程度上）挤占常规气体的份额。

7. 结论

7.1 可行方案的比较

针对 EIP-8037 研究了几种不同的计量 Gas 方程。在一种极端情况下，计量 Gas 可以计算为两种资源消耗量的max 。如果目标值是限制值的一半，那么在均衡状态下，一种资源的消耗量可能会非常低，因为需求量较高的资源在长期内无法超过其目标值。为了弥补这一点，如果重新定价后状态创建的需求远超预期，则可以将目标值调整得更接近突发约束常规 Gas 的限制值，以保持可扩展性。

另一方面，计量气体可以计算为两种资源的average 。当一种资源的需求量相对高于另一种时，其长期使用量可以略有增加，从而使使用量较低的资源在均衡状态下不至于被压得太低。然而，如果普通气体比状态生成气体更受欢迎，那么普通气体的目标值就不能不对称地设定得更接近其极限值，因为长期均衡使用量可能已经接近于1。

可以通过加权平均值或欧氏范数来计算两种极端情况之间的折衷方案。这些折衷方案允许目标/限制比率不对称，但比使用max函数时更为保守。

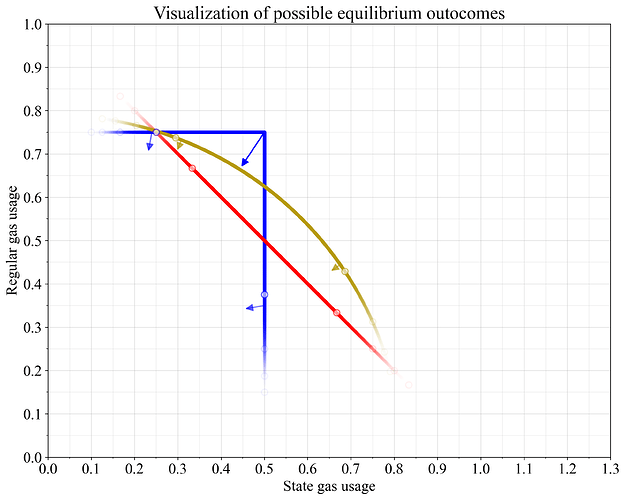
图 8 展示了之前在图 2、图 6 和图 7 中呈现的所有三种方案，但仅关注基本费用不变 (0%) 的均衡点。一个重要的方面是，当资源需求与研究人员预先设定的假设存在差异时（尤其是在初始假设两种资源的需求均达到目标水平的情况下），系统会如何运行。因此，图中用圆圈标记了两种资源均衡利用率分别为 {2:1, 3:1, 4:1, 5:1} 时的结果。为了便于可视化，不同线条的透明度采用正态分布进行设置，比率的每个整数倍增加（每个圆圈）代表一个标准差。

如第 2 节所述， max函数的非线性特性会降低均衡利用率，尤其是在目标交叉点附近。这一特性用箭头表示。对于接近目标交叉点的max函数，这种影响最为显著。而对于平均函数，区块层面的不匹配则会导致长期利用率沿着 0% 线移动，而不是垂直于该线。

图 8 2587×2066 252 KB

图 8展示了本文研究的计量气体方程可能出现的结果。圆圈表示当一种资源相对于另一种资源的消耗比例分别为 {2:1, 3:1, 4:1, 5:1} 时的均衡结果。箭头表示在非线性计量气体方程下，当各个区块的资源分布不均匀时，长期利用率会下降。

7.2 需求、目标设定和天然气限额的变化

EIP-8011 等计量方法存在一个问题，而 EIP-8075 则不存在这个问题，即难以预测价格变化将如何影响需求。无论采用何种计量天然气方程，研究人员都必须考虑他们认为新的有效天然气价格将如何影响需求，并据此设计相应的处理流程。

需要注意的是，在特定 Gas 价格下，需求量未必与协议设定的“目标”相符。这里不存在像 EIP-1559、EIP-4844 或 EIP-8075 那样的完全“目标设定”，即通过调整价格来确保一定的利用率。如果状态 Gas 的需求量仅占常规 Gas 的 3/7，那么忽略区块波动，即使状态 Gas 的消耗量翻倍，在max函数下也不会影响 Gas 价格。为了使状态 Gas 的计量水平始终能够影响 Gas 价格（从而构成真正的目标设定），可以采用转移函数，根据不同的计量水平对 Gas 进行计量和收费。用户将按规定的 Gas 价格支付交易费用，但max函数可以应用于例如以 7/3 的更高计量水平计量的 Gas。

该策略与第 5 节中针对非对称比率执行的归一化步骤有些类似，但随后也应用于对称比率下，以补偿未达到目标值的需求。然而，这也意味着状态创建对整体 gas 价格的影响相对于用户实际支付的 gas 费用而言会过大。考虑到这一点，在需求失衡的情况下，采用比max函数更宽松的方案似乎更具吸引力。第 6 节也值得参考，因为它降低了状态创建 gas 对定价的影响。这种方法也可以应用于例如average函数的情况。

一个相关的问题是如何处理 gas 上限的变化。随着 gas 上限的提高，状态创建量也会随之增加。为了控制状态创建量，一种解决方案是根据 gas 上限的变化调整其 gas 价格，例如，如本文所述。正如难以预测一次性重新定价对需求的影响一样，预测这种渐进式变化的影响也同样困难。当 gas 上限翻倍时，状态创建的 gas 价格并非简单地翻倍即可。正确的调整取决于需求弹性，而目前很难对此进行预测。然而，当然可以尽力尝试，然后在下一次硬分叉时根据观察到的弹性进行调整。这通常是多维计量下必须采取的方法，涉及初始硬分叉中做出的许多假设。