这项研究是与@AnteroE合作完成的。
本文探讨了缩短以太坊交易槽时间对去中心化交易所(CEX)活动的影响,重点关注中心化交易所(CEX)与去中心化交易所(DEX)之间的套利行为。我们构建了一个交易模型,其中交易者的DEX交易无法保证成功,交易者在决定是否进行套利时会明确考虑这种执行风险。
我们将以太坊默认的 12 秒时隙时间环境下的代理行为与提供 1 秒子时隙执行的更快时隙时间环境下的代理行为进行比较。模拟结果基于 2025 年 7 月至 9 月的币安和 Uniswap v3 数据进行校准,结果表明,更快的时隙时间平均可使套利交易数量增加 535%,交易量增加 203%。
1 秒子槽下 CEX-DEX 套利活动的增加是由成功和失败交易结果的方差减小所驱动的,从而提高了风险调整后的收益,使 CEX-DEX 套利更具吸引力。
TLDR
- 对于风险规避型代理人而言,如果其在去中心化交易所 (DEX) 交易中成功完成交易的概率为 35%,那么当确认时间从 12 秒缩短到 1 秒时,交易数量将增加 535%,交易量将增加高达 203%。
- 风险规避型代理人的交易量增长 535% 可分解为两个渠道:371% 来自可组合性,另外 164 个百分点来自去风险化。
- 1 秒子槽下 CEX-DEX 套利活动的增加是由成功和失败交易结果的方差减小所驱动的,从而提高了风险调整后的收益。
- 与记录实际套利结果的实证研究不同,我们构建了中心交易所-去中心交易所套利者在执行不确定性下面临的决策模型。这种视角揭示了为何观察到的套利活动可能严重低估了对更快执行速度的潜在需求:许多有利可图的机会并非不存在,而是因为理性交易者在当前的确认时间下选择放弃尝试。
- 我们专注于无需协议级更改即可提供的执行保证,这使得我们的分析适用于一系列可能的机制设计,包括但不限于预确认。
- 在合理的获胜概率变化( \alpha \in \{0.20,0.35,0.50\} α ∈ { 0.20 , 0.35 , 0.50 } )和风险厌恶程度变化( \lambda \in \{0,0.01,0.03\} λ ∈ { 0 , 0.01 , 0.03 } )下,结果依然稳健。
1. 为什么我们要关注减少交易时段时间?
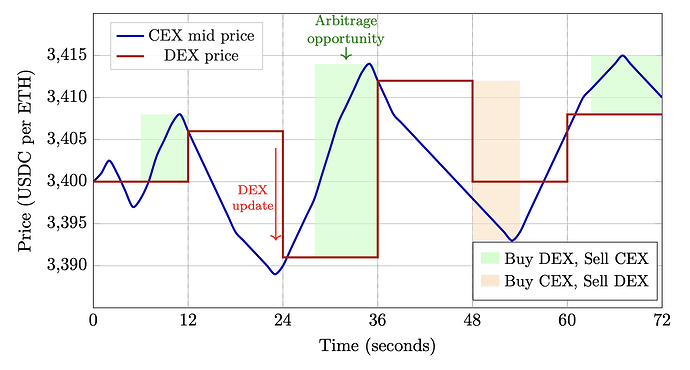
以太坊上最活跃的去中心化交易所 (DEX) 交易量来源之一是中心化交易所和去中心化交易所之间的套利。策略很简单:当中心化交易所(例如币安)和去中心化交易所(例如 Uniswap)的价格存在差异时,交易者可以利用这种机会,同时在价格较低的中心化交易所买入,在价格较高的中心化交易所卖出,从而赚取价差。
然而,这种策略并非没有风险:虽然CEX交易几乎瞬间完成,但DEX交易必须等待区块被包含,而区块被包含并不能保证成功。DEX交易可能因多种原因失败,例如优先级费用不足、其他交易者抢先交易、延迟,甚至区块构建者审查交易。
本文重点探讨去中心化交易所(DEX)交易段执行的风险及其与交易时长的关系。我们构建了一个交易代理模型,该代理已知其链上交易可能失败,并将这种不确定性纳入其入场和出场决策中。模型的核心在于:代理面临一个已知的DEX交易段成功执行概率α ,如果交易失败,则必须决定如何管理由此产生的delta风险敞口。
本文的动机源于对以太坊交易时长缩短将如何影响去中心化交易所(DEX)交易量最大部分的兴趣。我们设想了一种以1秒子时隙运行的理论协议,与以太坊原生的12秒时隙相比,该协议能为交易者提供更快的反馈循环。我们探讨的问题是:更快的执行速度如何改变套利者的行为,以及对DEX活动会产生哪些后续影响?
2. 模拟场景和数据
2.1 执行机制
该模拟的核心目标是量化更快的执行速度保证如何改变套利者的行为和市场结果。我们分别在两种执行机制下运行并行模拟:
| 政权 | 描述 |
|---|---|
| 12 秒槽 | DEX交易只能在以太坊槽位边界执行,每12秒执行一次。因此,在当前环境下,套利者面临着较大的执行窗口和相应的不确定性。 |
| 1秒子槽 | DEX交易可通过子槽确认每秒执行一次。这种改进的环境为套利者提供了更快的执行速度保证。 |
2.2 环境配置
我们评估了多种环境配置下的代理人行为,以检验研究结果的稳健性。每种配置都结合了两种二元设计选择,分别代表市场微观结构的不同方面。
CEX-DEX价格回归:启用后,子槽DEX价格会在套利事件之间通过回归机制逐渐向CEX价格靠拢。这可以捕捉到独立于直接套利之外的知情交易。
噪声交易:启用后,模拟程序会加入随机的非套利交易,其频率和价格影响均取自根据数据估计的经验分布。这可以捕捉到零售交易流量和其他与中心交易所-去中心交易所套利无关的交易活动。
2.3 数据
我们使用 2025 年 7 月至 9 月的数据,包括币安的毫秒级最佳买价和卖价,以及 Uniswap v3 ETH-USDC 池在 30 个基点、5 个基点和 1 个基点档位的所有兑换交易。
2.4 关键参数
| 范围 | 价值 | 描述 |
|---|---|---|
| α α | 0.35 | 特工 1 的获胜概率 |
| λ | 0.01 | 风险厌恶系数 |
| θ | 0 | 准入门槛 |
| 回滚窗口 | 300秒 | CEX-DEX 复原区间 |
| 蒙特卡洛路径 | 16 | 每个节点的路径 |
| 决策等待期 | 3秒 | 最长等待时间 |
| \bar{k} ¯ k | 3 | 强制关闭前的最大失败尝试次数 |
2.5 主要假设
在执行方面:所有验证者都选择提供快速执行保证;因此,不会错过任何交易槽位,DEX 交易可以每秒发生一次;gas 费用为零;代理不会耗尽资金,这意味着流动性限制不会影响执行,并且除了 DEX 池费用外没有其他费用。
在套利方面:每个区块顶部的套利机会都会被执行;套利以最佳交易规模执行,使 DEX 价格与 CEX 买价或卖价相差一个资金池费用;币安上最佳买价和卖价处存在无限流动性,并且在币安上执行是即时且有保障的。
关于市场结构: DEX 资金池是恒定乘积(Uniswap v2 风格);流动性恒定,除了交易费用的增加外,所有资金池的初始流动性都相同,以便进行比较。
3. 模型和结果
3.1 模型推导
DEX价格插值
该模拟框架模拟了中心化交易所和去中心化交易所价格随时间变化的相互作用。历史去中心化交易所(DEX)价格数据易于获取,可用于12秒时间段的基准模拟。对于更快的交易环境,我们需要一个框架来插值这些价格,以适应1秒的子时间段。
我们的框架包含三个组成部分。首先,我们从当前时隙的历史价格开始,该价格同时也是初始子时隙的价格。接下来,我们根据第(i-1) 个子时隙的价格 p^{\text{DEX}} (t_{i- 1 } ) p DEX ( t i − 1 ) 推导出第i个子时隙的价格p^{\text{DEX}} ( t_i ) p DEX ( t i ) 。为此,我们应用了以下方法:(1) 如果存在,则应用来自前一个时隙的套利交易;(2) CEX-DEX 价格回归,以模拟 DEX 价格如何在套利事件之间根据链下信息进行调整;以及 (3) 噪声交易,以捕捉非套利 DEX 活动。
噪声交易。我们根据交易特征将Uniswap v3的历史交易分为套利交易和噪声交易。如果一笔交易满足以下全部四个条件,则被视为套利交易:(1)它是区块中的第一笔交易;(2)交易前CEX-DEX价格差异超过交易池费用;(3)交易使DEX价格向CEX价格靠拢;(4)交易后价格差异仍然等于或高于交易池费用。所有其他交易均被归类为噪声交易。
CEX-DEX价格回归。其思路是估计DEX价格通常会对给定的CEX价格变动做出多大的响应,然后利用这种关系在套利事件之间将DEX价格回归到CEX价格。我们将时间轴划分为半开放区间F_k = (\tau_{k-1}, \tau_k] F k = ( τ k − 1 , τ k ],并在每个区间内估计一个线性模型:
对于区间F_k内的任何时间戳t_i ,其中CEX 价格已被观测到但 DEX 价格尚未更新,我们预测:
并得到反转后的DEX价格:
交易代理模型
CEX-DEX套利利用中心化交易所和去中心化交易所之间的价格差异。其核心风险在于交易的两部分执行异步。假设币安交易所流动性无限,且交易即时执行并有保障,则CEX部分的结算不存在风险,但DEX部分的结算需要被打包进区块。如果DEX交易未能成功,交易者将面临未对冲的风险敞口。
我们构建了一个能够明确考虑这种风险的代理模型。该代理在任何套利尝试中,都有固定的概率α ∈ ( 0,1 )成功完成去中心化交易所 (DEX) 部分的交割。如果交割失败,代理必须决定如何处理由此产生的风险敞口:立即在中心化交易所 (CEX) 平仓、在下一个交易时段重试 DEX 交易,或者等待更好的交易条件。
令p^{\text{CEX}}_{\text{bid}}(t) p CEX买价( t )和p^{\text{CEX}}_{\text{ask}}(t) p CEX卖价( t )分别表示 CEX 的买价和卖价,令p^{\text{DEX}}(t_n) p DEX ( t n )表示 DEX 在n时刻的价格,其中t_n = n\tau t n = n τ是n时刻的时间戳,而\tau τ是时刻的持续时间。
简单模型。在简单模型中,代理人会尝试抓住每一个检测到的套利机会,而不考虑执行风险。以概率α ,去中心化交易所 (DEX) 的套利操作成功,代理人获得全部套利利润:
以概率1-α (1 - α) ,DEX 交易失败。代理人已在 CEX 卖出,现在必须平仓。在简单模型中,代理人只需在一秒钟后在 CEX 买回即可:
风险规避模型。风险规避模型赋予代理人两种简单模型所不具备的能力:基于风险调整后的预期收益进行选择性入场,以及在交易失败时做出最优的备选方案。
进入决策。只有当风险调整后的预期利润超过阈值θ时,代理人才会进入套利机会:
在哪里:
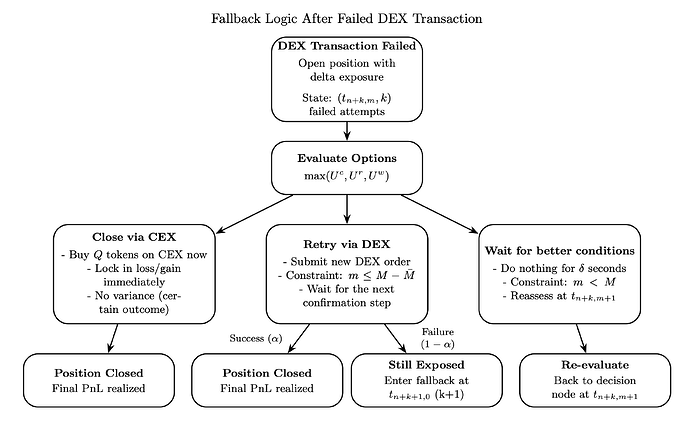
回退逻辑。当去中心化交易所 (DEX) 交易失败时,智能体持有一个开放的中心化交易所 (CEX) 头寸,该头寸最终必须平仓。在每个决策点t_{n+k,m} t n + k , m (位于时隙n+k n + k ,子时隙m m ),经过k次DEX 交易失败后,智能体会在以下三个选项中选择一个:
- 立即平仓:按当前卖价在 CEX 交易所买回。
- 在 DEX 上重试:以当前 DEX 价格提交新的 DEX 买单,并等待下一个交易时段。
- 等待:在一个时间步长内什么也不做,并在t_{n+k,m+1} t n + k , m + 1重新评估。
代理人选择风险调整效用最高的方案:
受以下约束:只有在时隙结束前有足够的时间时才可重试( m \leq M - \bar{M} m ≤ M − ¯ M ),只有在时隙内才可等待( m < M m < M ),并且在\bar{k} ¯ k次尝试失败后,代理必须关闭。
计算方法。我们采用反向归纳法,并在每个节点进行蒙特卡罗估计来求解价值函数。终止条件为在k = \bar{k} 和k = ¯ k处强制闭包。递归过程采用两层嵌套循环:外层循环遍历失败的尝试( k = \bar{k}-1, \ldots, 0和k = ¯ k − 1 , … , 0 ),内层循环遍历每个槽位内的子槽位( m = M, \ldots, 0和m = M , … , 0 )。在每个状态下,我们模拟N条价格路径来估计每个选项的期望和方差,然后选择风险调整效用最高的选项。
用于期望值计算的价格动态。我们假设CEX对数收益率服从高斯随机游走:
买价和卖价分别为p^{\text{CEX}}_{\text{bid}} = (1-\beta) p^{\text{CEX}}_{\text{mid}} p CEX bid = ( 1 − β ) p CEX mid和p^{\text{CEX}}_{\text{ask}} = (1+\beta) p^{\text{CEX}}_{\text{mid}} p CEX ask = ( 1 + β ) p CEX mid其中\beta β为半价差。
竞争结构
该仿真模型模拟了运行 CEX-DEX 套利机器人的代理之间的竞争动态。代理 1 代表我们详细分析其行为的参与者,而代理 2 代表所有其他市场参与者的总体行为。当出现套利机会时,多个代理可能会尝试抓住它,但区块链的限制确保只有一笔交易能够成功。当代理 1 尝试套利机会时,其获胜的概率为α 。当代理 1 失败或选择不尝试其 DEX 交易时,代理 2 将自动成功并获得套利利润。
3.2 对交易频率的影响
我们将交易频率定义为代理人完成的交易数量。在简单模型中,所有资金池的交易数量均显著增加。在所有配置和费用等级下,简单模型的交易频率增幅在 218% 到 663% 之间。风险规避模型的交易频率增幅更大,交易数量增幅在 294% 到 1386% 之间。然而,值得注意的是,大多数情况下增幅低于 600%,1386% 的增幅仅出现在一种配置中,尽管百分比变化很大,但交易的绝对数量却很小。
不同费用等级的模式反映了不同价差水平下的套利经济效益。低费用池的价差更小,套利机会也更多。在12秒确认时间下,许多套利机会并不值得追求,因为执行窗口足够长,不利的价格波动就可能抹去微薄的利润。而在1秒确认时间下,风险被压缩,更多微利机会变得可行。
简单代理(跨池加权平均值):
| 配置 | Δ Δ ETH Vol. | Δ Δ Txns |
|---|---|---|
| 无回滚,无噪音 | +158% | +378% |
| 无回滚,噪音 | +148% | +356% |
| 回落,无噪音 | +211% | +412% |
| 回落,噪声 | +188% | +387% |
风险规避型代理人(各资金池的加权平均值):
| 配置 | Δ Δ ETH Vol. | Δ Δ Txns |
|---|---|---|
| 无回滚,无噪音 | +159% | +378% |
| 无回滚,噪音 | +163% | +503% |
| 回落,无噪音 | +212% | +437% |
| 回落,噪声 | +243% | +567% |
对于简单模型,不同资金池的交易数量增幅的加权平均值在 356% 到 412% 之间,具体增幅取决于配置;而有无回滚配置时的噪声平均值为 371%。类似地,对于风险规避模型,加权增幅在 378% 到 567% 之间,两种配置的平均值为 535%。
效应分解
风险规避型代理人的交易量增长535%实际上可以分解为两个渠道。简单代理人的交易量增长371%完全源于可组合性的提高:更频繁的确认机会使代理人能够在每个交易时段内识别并尝试更多套利机会。额外的164个百分点则来自风险规避*:更快的确认速度压缩了回退期内价格结果的波动,使得风险调整后的预期利润更频繁地超过入场阈值。
3.3 对交易量的影响
以以太坊计价的交易量展现出比交易笔数变化更为微妙的模式。在简单模型中,交易量的变化幅度根据配置的不同,从 98% 到 273% 不等。与交易频率类似,对于 30 个基点的资金池,增幅更接近范围的下限;而对于 5 个基点和 1 个基点的资金池,增幅则更接近范围的上限。风险规避模型也呈现出类似的模式,增幅范围从 121% 到 375% 不等。
交易量的增长主要集中在低费率的资金池中。其背后的逻辑是:当更多边际交易机会变得可行时,平均交易规模可能会下降(因为边际交易机会的最优交易规模往往较小),但总交易次数的增加足以提升总交易量。而在高费率的资金池中,由于交易机会本身规模就很大且出现频率较低,更快的确认速度并不会显著扩大可行交易机会的范围。
值得注意的是,这些范围代表了不同配置下的结果;然而,由于模型中没有包含 gas 费用,这些范围的上限可能会高估 1 个基点和 5 个基点资金池的增长,因为在实践中,频繁小额交易的经济可行性会受到交易成本的限制。
根据不同资金池的套利交易量对交易量增长进行加权,简单模型下三个资金池的平均交易量增长在 148% 至 211% 之间,平均值为 168%。同样,风险规避模型下,总体增长在 159% 至 243% 之间,平均值为 203%。
3.4 按池划分的详细结果
简单代理(30 bps 池):
| 配置 | ΔPnL | Δ Δ ETH Vol. | \Delta Δ USDC Vol. | Δ Δ Txns |
|---|---|---|---|---|
| 无回滚,无噪音 | +113% | +118% | +116% | +294% |
| 无回滚,噪音 | +97% | +98% | +97% | +218% |
| 回落,无噪音 | +276% | +273% | +265% | +663% |
| 回落,噪声 | +218% | +211% | +205% | +478% |
简单代理(5 bps 池):
| 配置 | ΔPnL | Δ Δ ETH Vol. | \Delta Δ USDC Vol. | Δ Δ Txns |
|---|---|---|---|---|
| 无回滚,无噪音 | +138% | +158% | +157% | +308% |
| 无回滚,噪音 | +135% | +151% | +150% | +274% |
| 回落,无噪音 | +147% | +174% | +172% | +345% |
| 回落,噪声 | +144% | +165% | +164% | +313% |
简单代理(1 bp 池):
| 配置 | ΔPnL | Δ Δ ETH Vol. | \Delta Δ USDC Vol. | Δ Δ Txns |
|---|---|---|---|---|
| 无回滚,无噪音 | +195% | +203% | +202% | +420% |
| 无回滚,噪音 | +207% | +200% | +199% | +408% |
| 回落,无噪音 | +207% | +205% | +204% | +432% |
| 回落,噪声 | +212% | +202% | +201% | +420% |
风险规避型代理人(30 个基点资金池):
注意:对于下表,需要注意的是,虽然某些配置的交易数量百分比变化很大,但绝对值却很小。
| 配置 | ΔPnL | Δ Δ ETH Vol. | \Delta Δ USDC Vol. | Δ Δ Txns |
|---|---|---|---|---|
| 无回滚,无噪音 | +114% | +121% | +119% | +294% |
| 无回滚,噪音 | +119% | +126% | +124% | +336% |
| 回落,无噪音 | +282% | +274% | +267% | +639% |
| 回落,噪声 | +365% | +375% | +365% | +1386% |
风险规避型代理人(5个基点资金池):
| 配置 | ΔPnL | Δ Δ ETH Vol. | \Delta Δ USDC Vol. | Δ Δ Txns |
|---|---|---|---|---|
| 无回滚,无噪音 | +135% | +158% | +157% | +307% |
| 无回滚,噪音 | +137% | +162% | +161% | +444% |
| 回落,无噪音 | +145% | +174% | +173% | +345% |
| 回落,噪声 | +147% | +179% | +178% | +500% |
风险规避型代理人(1 bp 池):
| 配置 | \Delta Δ PnL | Δ Δ ETH Vol. | \Delta Δ USDC Vol. | Δ Δ Txns |
|---|---|---|---|---|
| 无回滚,无噪音 | +151% | +205% | +204% | +419% |
| 无回滚,噪音 | +151% | +205% | +205% | +544% |
| 回落,无噪音 | +158% | +208% | +207% | +472% |
| 回落,噪声 | +161% | +206% | +206% | +554% |
3.5 稳健性分析
为了评估这些发现的稳健性,我们对风险厌恶模型在反转和噪声交易配置下进行了一组额外的模拟。我们改变了代理人 1 的获胜概率α ∈ { 0.20 , 0.35 , 0.50 }和风险厌恶参数λ ∈ { 0 , 0.01 , 0.03 } ,并比较了确认间隔从 12 秒缩短到 1 秒时的结果。
在 5 基点池中,该网格所有组合的交易笔数增加了 416%–530%,ETH 交易量增加了 146%–186%。在 30 基点池中,交易笔数增加了 1152%–1468%,ETH 交易量变化范围在 317% 到 385% 之间。
总体而言,在 12 秒确认间隔与 1 秒确认间隔下,具有相同参数的代理的交易数量和交易量的变化幅度相同,这表明主要结果对获胜概率和风险厌恶的合理变化具有稳健性。
4. 讨论和后续步骤
本研究探讨了缩短区块链执行时间如何影响去中心化交易所(CEX)的活动,重点关注CEX-DEX套利者的行为。我们的贡献兼具方法论和实证性:我们开发了一个模拟框架,该框架结合了经验价格锚定、噪声交易动态、CEX-DEX套利机制以及风险规避决策模型。我们建模的主体认真对待执行风险,将DEX交易的不确定性纳入其入场决策和备选策略中。这种设置捕捉到了链上交易的一个基本现实,而此前的研究大多忽略了这一点。
在对代理人风险偏好和纳入概率做出合理假设的前提下,从12秒到1秒的执行环境转变可使套利交易数量增加535%,且这种影响主要集中在低费率资金池,因为在这些资金池中,边际套利机会变得可行。更快的执行速度还能缩短交易失败恢复期间价格不利波动的时间窗口,从而降低利润波动。
局限性。有几个局限性值得一提。我们的模型假设 gas 费用为零,这可能会高估低费用池中小额交易的可行性。此外,代理人在去中心化交易所 (DEX) 上完成交易的概率是固定的,而不是由竞争内生决定的;在均衡状态下,更快的执行速度可能会吸引更多套利者,从而压缩α 。这些扩展有待未来研究。