
作者:Aram Jivanyan、Albert Garreta、Hayk Hovhanissyan、Ignacio Manzur、Isaac Villalobos-Gutiérrez 和 Michal Zajac。
在这篇文章中,我们研究了当一个人必须同时提供许多证明时摊销成本的问题。我们称之为“打包”的方法适用于基于 FRI 的 SNARK(例如 ethSTARK、Plonky2、RISC0、BoojumETC)。它允许生成一个证明,证明许多证人满足某些约束,同时减少验证者的工作和证明大小(与为每个证人生成证明并由验证者检查其中每个证据相比)。我们通过实验证明该技术在实践中是有用的。
在即将发表的技术论文中,我们将更深入地研究打包机制,并将讨论聚合基于 FRI 的 SNARK 证明任务的其他方法。这项工作在某种程度上可以看作是社区最近为 SNARK 证明任务设计累积方法(例如折叠方案)所做的努力的延续。然而,在基于 FRI 的 SNARK 环境中,人们面临着没有同态承诺方案的不便,这需要与最近开发的方法截然不同的方法。
更详细地说,打包是一种批量证明生成方法,允许证明者为潜在的不同实例生成证人可满足性的单一证明。打包带来的主要改进是证明者和验证者在所有实例上仅执行一次 FRI 低度测试。与顺序证明每个见证人的可满足性相比,验证者时间和打包证明的证明大小都减少了,证明者时间略有减少。我们的基准测试表明,对于典型的迹线(216 行,100 列),验证者时间缩短约 2 倍,证明大小减少约 3 倍。
正如我们稍后解释的,这种方法与长递归证明任务的结合特别相关。例如,当单个证明者递归地生成多个见证人有效性的证明时,证明者可以使用“递归层”之间的打包来证明有关下一层较小验证者和较小见证人的陈述。
我们注意到,打包方法可以“聚合”基于 FRI 的 SNARK 证明的潜在不同关系和类型的证明任务。例如,对于两种语言 L₁、L2 和两个实例 x₁、x2,打包可以分摊使用 ethSTARK 证明 x₁∈L₁ 的成本,以及使用 Plonky2 证明 x2∈L2 的成本。
在下一节中,我们将简要概述打包技术及其性能改进。之后,我们讨论它的一些潜在应用。我们通过展示实验结果来遵循这一点。我们推迟了对该技术的正式描述及其相应的健全性分析,以供我们即将发表的技术论文(该论文还将描述进一步的优化技术)。
概述
我们专门讨论 ethSTARK [Sta21] 协议(有时称为 STARK)的方法。然而,该技术可以适用于任何“基于 FRI 的 SNARK”(在 [BGK+23] 的意义上)。回想一下,ethSTARK IOP 遵循下面的蓝图。下面,𝔽表示有限域,𝕂是𝔽的有限扩展。
- 见证者是预言机函数 f₁, …, fₛ: D ⊂ 𝕂→ 𝕂,据说是某个有界次数 d 的多项式。这里,D 是乘法子群 D₀ ⊂ 𝔽* 的 𝕂 中的陪集。陪集 D 称为评估域。子群 D₀ 包含大小为 d+1 的子群 H₀=<g>,称为迹域。后者与 AIR 执行跟踪的行一一对应。这里,d是度数界限。我们将 fᵢ(X) 称为见证图。
- 约束是函数 fᵢ(X) 中的多项式表达式(以及一些移位 fᵢ(gʲ⋅X))。每个这样的多项式都应该在整个迹域 H₀(或 H₀ 的子集,但为了简单起见,我们假设所有约束都在所有 H₀ 上消失)上消失。
- 例如,约束的形式可能为 Q(f₁(X), f2(g⋅X)) = f₁(X)2 + f2(f⋅X)3。那么,这个表达式应该是一个在 H₀ 上消失的“低次”多项式,这意味着对于所有 h∈ H₀,f₁(h)2=f2(g⋅h)3。
- 接下来,验证者对用于产生单个约束 C: H → 𝕂 的随机性进行采样,作为每个约束的随机线性组合。我们将 C(X) 称为DEEP-ALI 约束。例如,如果约束为 Q₁(f₁(X), f2(g⋅X)) 和 Q2(f₁(g2⋅C), f2(X)),则组合约束为映射 C(X) := Q(f₁(X), f2(g⋅X)) + α ⋅ Q2(f₁(g2⋅C), f2(X)),其中 α 是随机元素。同样,这个约束被认为是一个在 H₀ 上消失的低次多项式。
- 现在,证明者通过证明 C(X)=Z(X)⋅q(X) 来证明 C(X) 满足上述性质,其中 Z(X) 是迹域 H₀ 的消失多项式,q( X) 是 C(X) 除以 Z(X) 的商,它应该是低次多项式。为此,证明者向验证者发送一个关于商图q(X) 的预言。然后,执行以下检查:
- 检查 C(X)=Z(X)⋅q(X) 在从 𝕂 采样的单个随机点 ψ(称为深度查询点)处是否成立。为了进行此检查,证明者向验证者发送映射 q(X) 和 {fᵢ(X)} 在 ψ 和移位 gʲ⋅ ψ 处的评估,我们分别宽松地表示 q_ψ 和 {fᵢⱼ}。
- 验证者现在需要确保接收到的值是正确的,并且映射 {fᵢ(X)}, q(X) 的度数较低。为此,证明者和验证者使用 Batch-FRI 协议来显示商 (fᵢ(X)-fᵢⱼ)/(X-gʲ⋅Σ) 和 (V(X)-q_Σ)/(X-Σ ) 是低次多项式。
- 回想一下,Batch-FRI 是一种协议,用于证明映射 h₁, …, hₘ: D\to 𝔽 的集合接近于 ≤ d 次的多项式(更技术地说,Batch-FRI 证明这些映射具有 δ 相关性) Reed-Solomon 代码 RS[𝔽, D, d+1]) 中的协议。该协议的工作原理是将 FRI 协议应用于映射 h₁、…、hₘ 的随机线性组合。我们将映射 (fᵢ(X)-fᵢⱼ)/(X-gʲ⋅Σ) 和 (V(X)-q_Σ)/(X-Σ) 的随机线性组合称为DEEP-FRI 函数。
我们技术中的主要观察结果是,通过使用 DEEP-ALI 约束组合和 Batch-FRI 组合的线性,我们可以将不同实例的跨证明代的约束和函数打包到单个组合约束和单个 DEEP-FRI 函数中。换句话说,当生成多个 ethSTARK 证明时,可以从所有单独的证明中获取所有 DEEP-ALI 约束的随机线性组合。然后,证明者和验证者针对生成的“全局”DEEP-ALI 约束执行上面的步骤 4。
当应用 Batch-FRI 时,我们还必须揭示对批处理图的评估域 D 的评估。当用 Merkle 承诺实例化时,我们将见证图和商图的所有评估打包在同一个 Merkle 叶子中 D 中的同一点(与 [MAGABMMT23] 中类似)。即,按照上面的表示法,默克尔树中的叶子看起来像 Hash(h₁(a), …, hₘ(a)),其中 a∈D 和 h₁, …, hₘ 是在证明。请注意,这不适用于 Batch-FRI 内轮中的 Merkle 树。
在下文中,为了满足 N 个见证人对 N 个实例(这些实例可以是 Plonkish、AIR、RAP 实例ETC)的可满足性,我们将“顺序验证者”称为检查基于 FRI 的证明的验证者(这些可以是通过使用 Plonky2、ethSTARK、RISC0ETC按顺序为每个实例生成。 “打包验证者”将指检查 STARKPacked 证明以确保每个见证人同时满足的验证者。相同的术语适用于证明者。
计算改进
与顺序证明不同实例的可满足性相反,这种改进主要来自于这样一个事实:现在 Merkle 承诺树更少,并且我们只对所有实例的可满足性执行一个 FRI 证明。发生第一点是因为我们在跨实例的每一轮中将所有相关函数的评估打包在同一个 Merkle 叶子中。正如我们所解释的,发生第二种情况是因为我们将所有商函数组合成一个 DEEP-FRI 函数。
更具体地说,就证明大小而言,该证明比顺序证明包含更少的 Merkle 根承诺。它还包括更少的 Merkle 取消提交路径,因为在所有打包实例中只执行一次 FRI。然而,对于打包证明者需要发送的功能评估数量,没有摊销。
关于打包验证器的工作,改进来自于它需要执行的哈希操作数量的减少。这是因为打包的验证者需要检查更少的 Merkle 解除承诺证明。更具体地说,对于涉及见证函数和商函数 q(X) 的 Merkle 树,打包验证器会散列更大的叶子来检查 Merkle 成员资格证明,但数量较少。此外,打包验证器检查与 FRI 的单次执行相对应的 Merkle 取消路径。
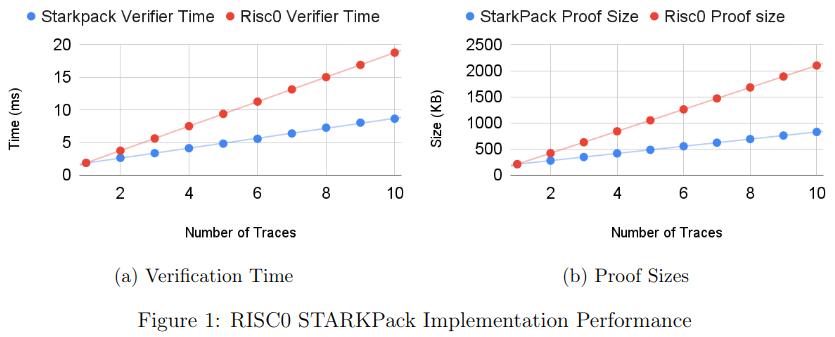
我们的初始基准(参见性能部分)表明,对于大小为 21⁶×100 的痕迹,与使用 Winterfell 顺序证明所有实例的可满足性相比,验证者时间和证明大小都减少了一半以上。在 RISC0 中,即使迹线具有固定数量的列 (275),验证器时间和证明大小的两倍改进仍然适用。当然,使用打包技术时要付出的代价是,随着批处理函数数量的增加,协议的可靠性会受到损失。在我们即将发布的技术文件中,我们正式证明了结构的健全性。
我们注意到,对于涉及见证函数和商函数 q(X) 的 Merkle 树,树第一层的 Merkle 解除承诺的成本不会通过我们的打包技术进行摊销。这是因为,如前所述,Merkle 树叶现在是评估向量(每个打包实例一个),因此,它们的大小随着打包实例的数量 N 线性增长。这部分解释了为什么在我们的实验中,打包验证器的工作量主要与迹线数量 N 呈线性关系。
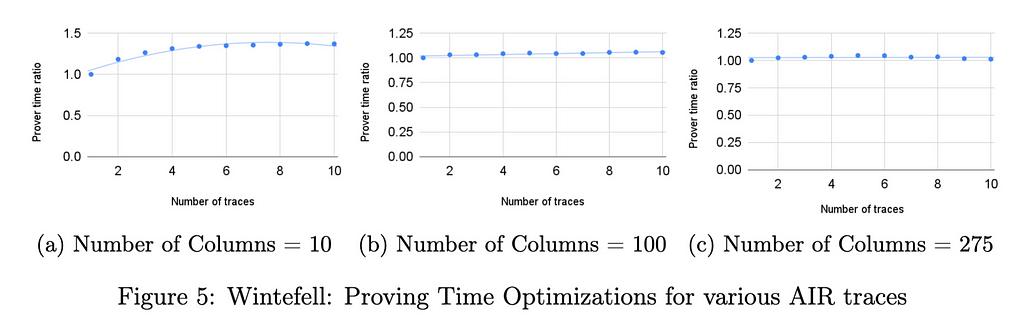
我们还认为该技术应该减少证明者时间,原因与减少验证者时间的原因类似。然而,随着列和打包实例数量的增长,计算组合 DEEP-ALI 约束所需的现场操作成本变得越来越重要。事实上,在我们的技术中,组合约束函数的计算没有摊销。随着我们批量处理的 RAP(或 AIR)实例中的列数增加,此成本占主导地位。我们在下面所示的基准测试中看到了这一点,对于大量列 (275),证明时间的改进约为 5%。
应用领域
我们在下面讨论一些封装技术的示例应用。如前所述,值得注意的是,我们可以为来自不同算术化的实例(例如 AIR 实例和 TurboPlonk(或 Plonk-ish)实例)的同时可满足性生成单一证明。这可能很有趣,具体取决于每个算术化提供的权衡以及不同的汇总使用具有不同算术化的证明系统的事实。此外,打包技术可以很容易地适应于打包不同校样系统的校样。
以下所有三个应用程序都依赖于相同的原理。即,在STARK递归证明之间使用打包方法来减小验证器电路和递归见证人的尺寸。因此,这会导致更快的递归证明器。在我们即将发表的技术论文中,我们将提供该策略带来的改进的基准。这些应该至少与我们在下一节中提供的简单初始基准一样有益。
Zk-Rollups: STARK 被著名的区块链公司广泛使用,构建称为 zk-rollups 的基于零知识证明的以太坊扩展解决方案。其中包括 StarkWare、 Polygon和 zkSync。最近,zkSync推出了基于Stark的L2解决方案,称为Boojum, Polygon部署了Polygon Miden,Starkware部署了Starknet;全部遵循相似的架构。从Polygon L2平台描述[Tea22]可以看出,在Layer 2上,每笔交易的正确性都通过独立的STARK证明来证明,并且所有交易的STARK证明都是独立但并行生成的。随后,这些独立的 STARK 证明通过递归证明组合来合并。生成的批量证明是递归 STARK 证明,确保所有输入证明的有效性。
我们的技术可以通过首先使用打包生成大量独立交易有效性的聚合证明来优化此工作流程,从而生成更小且更便宜的验证证明。因此,下一次递归迭代对于证明者来说更便宜,因为验证者电路和见证者都更小。这也可以在进一步的递归层中重复。
批量证明者: Starknet 推出了 SHARP,这是一个共享证明者系统,旨在链下处理批量的 Cairo 计算程序,其证明通过 Solidity 验证者合约在链上进行验证。由于STARK程序验证成本是多对数的,不同用户提交的各种Cairo程序可以在一个证明中批量验证,有效地将验证成本分配给所有程序。 SHARP 的最新版本采用了递归证明,每个程序在到达时最初都会单独进行验证。然后,这些单独的证明逐渐合并成递归证明。这个过程一直持续到最终证明准备好提交给链上验证者合约为止。我们提出的方法旨在提高 SHARP 递归证明的效率。我们的打包参数允许同时捆绑和证明多个语句,而不是单独证明每个程序(该过程后来成为递归证明者输入的一部分),从而产生更紧凑且更快验证的证明。这可以降低与生成递归证明相关的成本。
以太坊单槽最终性:以太坊基金会最近提出了构建单槽最终性共识系统的基本想法 [KKZM23]。该说明讨论了两种概念上不同的基于树和基于八卦的签名聚合拓扑,这两种拓扑都依赖于高效的签名聚合技术。聚合方案允许将多个签名合并为一个,并且还跟踪所有参与签名者的身份。此用例的困难在于每个参与者可以多次出现在聚合过程中。虽然有一些众所周知的签名方案可以实现高效聚合,例如 BLS,但当每个签名者可以在聚合过程中多次出现时,跟踪所有签名者仍然是通信复杂性方面的一个挑战。该说明讨论了一个名为“签名合并”的新概念,旨在通过零知识密码学有效解决此问题。用于实例化签名合并方案的建议方法之一是基于递归 STARK。递归 STARK 的特殊之处在于,计算包含其他 STARK 证明的验证,这反过来又验证与所提供的位字段相关的聚合签名的正确性。由此产生的递归 STARK 证明可确保传入的证明有效,并且其位域的并集等于所声称的结果。正如 [KKZM23] 中所解释的,用于签名合并的递归 STARK 的限制因素之一是证明的大小。这正是我们可以在递归生成最终证明之前首先利用打包证明聚合技术而不是独立的 STARK 证明的场景。同样,我们可以在每一层递归中应用相同的想法,并且这种方法总体上计算成本更低。
基准测试
我们已经在 Winterfell 和 RISC0 STARK 库中实现了打包技术。 Winterfell 允许写入任意迹线,并在优化迹线方面提供出色的灵活性。 RISC0 架构修复了 AIR 的某些结构元素,以便所有跟踪都具有独立于程序的固定数量 (275) 列。列数对最终批量证明和验证性能起着重要作用。
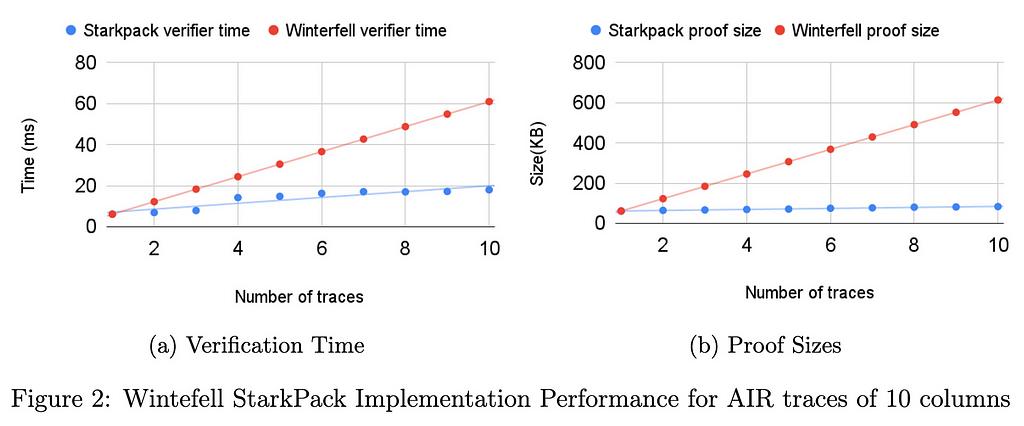
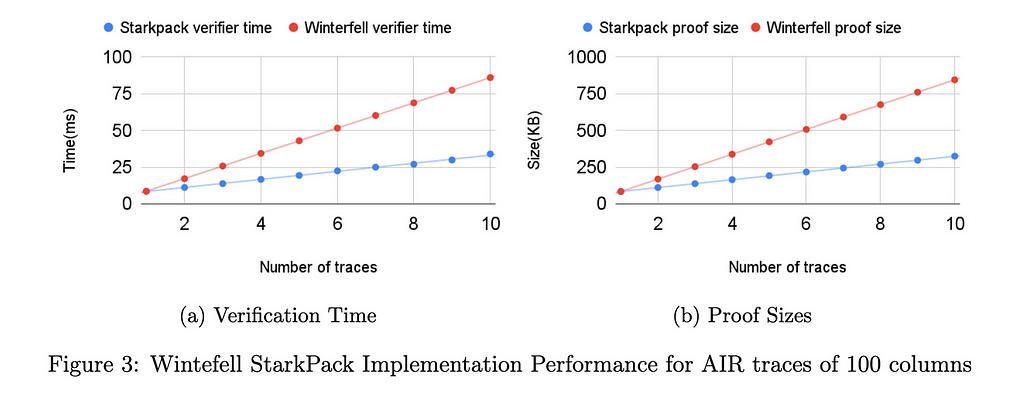
我们在两个库中运行了不同的基准测试。在所有基准测试中,行数固定为 21⁶。在临冬城,电路的列数从 10 到 275 不等,在每列计算从 i=1 到 i=21⁶ 的转换 x_{i+1} = x_i3 + 42。在 RISC0 中,对于证明知道数字的两个素因数的电路,迹线固定为 275 列。所有测试均在具有 32GB RAM 的 Intel i712700F 机器上运行。对于基准测试实例,证明时间的加速约为 5%。证明时间的优化可以忽略不计,这是由于列数较多。下面描述的针对具有较少列的迹线的 Winterfell 基准显示了证明时间优化如何取决于列数。
下图显示了在 RISC0 中针对 275 列的 AIR 跟踪以及在 Winterfell 中针对 10、100 和 275 列的跟踪实现的 StarkPack 性能改进。
结论
这篇文章旨在提供基于 FRI 的 SNARK 聚合方法的高级总结,强调我们最初的基准测试所证明的验证复杂性和证明大小方面的改进。技术论文中将对该技术和进一步的技术进行全面的解释,并进行合理性分析。
参考
[BGK+23] Alexander R. Block、Albert Garreta、Jonathan Katz、Justin Thaler、Pratyush Ranjan Tiwari 和 Michał Zając。周五的 Fiat-shamir 安全及相关问题。密码学 ePrint 档案,论文 2023/1071,2023, https://eprint.iacr.org/2023/1071。
[BSCI+20] Eli Ben-Sasson、Dan Carmon、Yuval Ishai、Swastik Kopparty 和 Shubhangi Saraf。里德-所罗门码的邻近间隙。密码学 ePrint 档案,论文 2020/654,2020。https ://eprint.iacr.org/2020/654。
[KKZM23] 乔治·卡迪亚纳基斯、德米特里·霍夫拉托维奇、张振飞和玛丽·马勒。大规模共识的签名合并,2023 年。https://ethresear.ch/t/signature-merging-for-large-scale-consensus/17386。
[KST21] Abhiram Kothapalli、Srinath Setty 和 Ioanna Tzialla。 Nova:来自折叠方案的递归零知识论证。密码学 ePrintArchive,论文 2021/370,2021。https ://eprint.iacr.org/2021/370。
[MAGABMMT23] Héctor Masip-Ardevol、Marc Guzmán-Albiol、Jordi Baylina-Melé 和 Jose Luis Muñoz-Tapia。 estark:用参数扩展斯塔克斯。密码学 ePrint 档案,论文 2023/474,2023。https ://eprint.iacr。 org/2023/474。
[Sta21] 斯塔克韦尔。 ethSTARK 文档。密码学 ePrint 档案,论文 2021/582,2021。https ://eprint.iacr.org/2021/582。
[Tea22] PolygonZero 团队。Polygon米登,2022。https :// Polygon。技术/多边形米登。
关于 Nethermind 研究
Nethermind Research融合了密码学、去中心化金融 (DeFi) 和协议研究领域,创造了增强各个领域的协同效应。
在这里阅读更多内容:
https://www.nethermind.io/applied-cryptography

STARKPack:聚合 STARK 以实现更短的证明和更快的验证,最初发布于Nethermind。 ETH在 Medium 上,人们通过强调和回应这个故事来继续对话。








