前言
您准备好探索zk-SNARK更复杂的一面了吗?在上一节中,我们学习了一些更高级的概念,例如算术电路和二次算术程序。在本节中,我们将通过深入研究另一个强大的概念来扩展我们的知识:椭圆曲线配对。
注意:深入理解椭圆曲线配对等主题有时对许多人来说是一个挑战。然而,这就是我们写这篇文章的原因——帮助您至少对此有一个基本的了解。
我的目标不仅是彻底解释椭圆曲线配对,而且使该主题更有趣且易于理解。希望通过本文,您将看到椭圆曲线对在数学和密码学中的强大功能,以及它们在zk-SNARK中的具体应用。
椭圆曲线
椭圆曲线是椭圆曲线密码学领域的一部分。这是一个复杂的课题,不是每个人都能轻易理解的。为了更好地理解它们,请查看我上一节中关于 ECC 的文章。
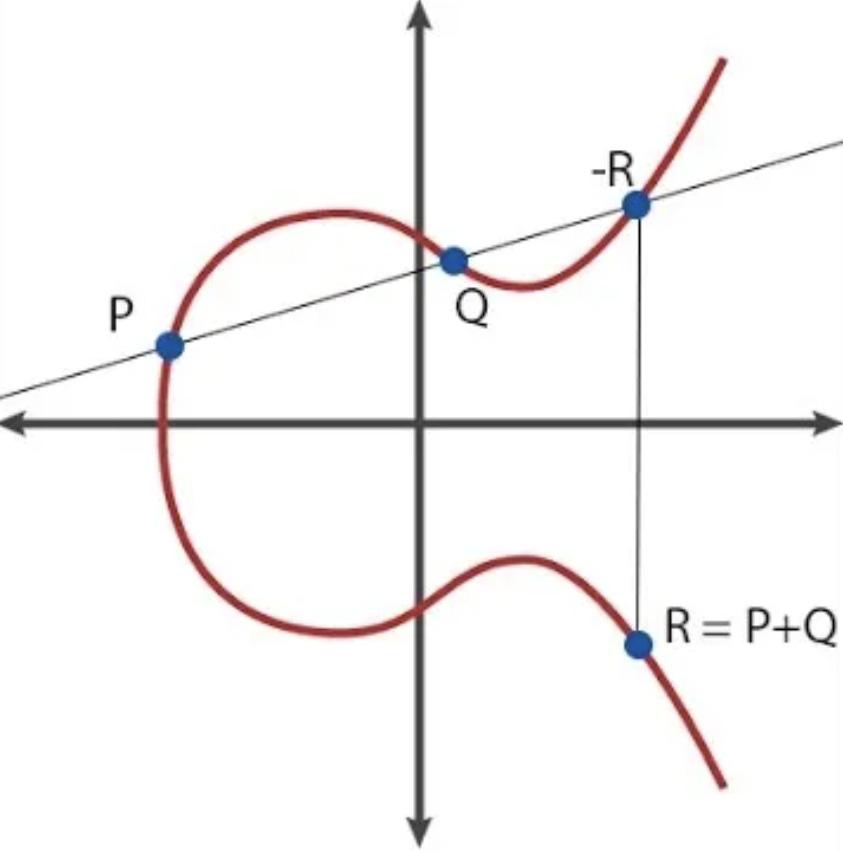
椭圆曲线密码学涉及二维空间中的“点” ,每个“点”由一对(x, y)坐标来表征。
执行点之间的加法和减法等数学运算有特定的规则,允许在已知其他点的情况下计算新点的坐标。
示例:计算坐标R = P + Q
您还可以将点与整数相乘,方法是重复将点与自身相加,次与该整数相同。
例如: P * n = P + P + … + P
这提供了一种在椭圆曲线密码学中执行数学运算的有效方法
在椭圆曲线上,有一个特殊的点,称为“无穷远点” ( O ),相当于点微积分中的数字 0, P + O = P始终成立。
曲线也有“阶” ;对于所有P ( P * (n+1) = P、P * (7*n + 5) = P * 5等等),存在一个数字 n,使得P * n = O。
此外,还有一个“生成点”(G ),可以理解为以某种方式代表数字1。理论上,曲线上的任何点(除了O )都可以是G 。
配对
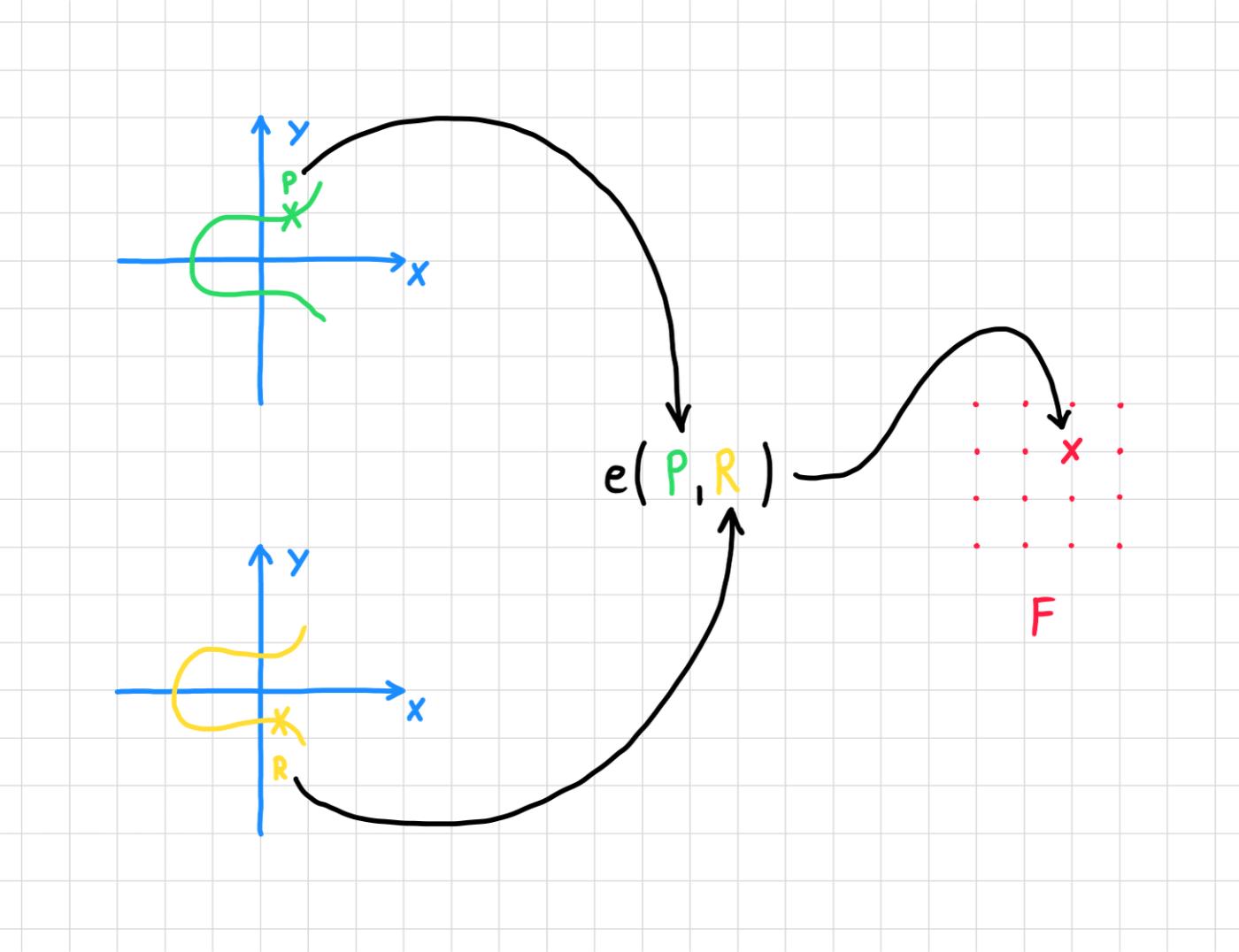
配对允许在椭圆曲线的点上测试更复杂的方程。
例如:
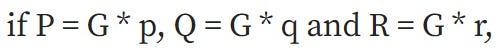
您可以仅根据P、Q和R检查p * q是否等于r 。
尽管有关p的信息可能会从P泄漏,但这种泄漏是经过仔细控制的。
配对允许检查二次约束。
例如:测试e(P, Q) * e(G, G * 5) = 1实际上是测试p * q + 5 = 0 。

是一种称为配对的操作。数学家也称其为双线性映射。这里的“双线性”将遵守以下规则:

请注意,您可以以任何方式使用+和*运算符,只要它们符合以下规则:

和
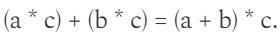
如果P、Q、R和S是简单数字,则使用以下表达式可以轻松制作简单的配对操作:
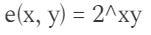
结果如下:
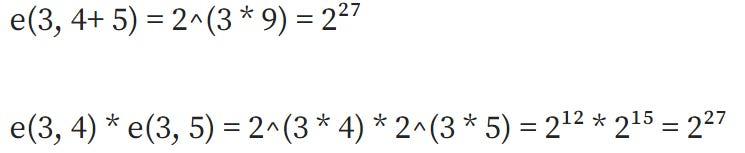
那就是平行线!
然而,这种简单的配对操作并不适合密码学,因为它们对简单整数进行操作并且太容易分析。
当您在执行配对操作时知道一个数字及其结果时,您可以轻松计算并找到剩余的数字。
我们使用像“黑匣子”这样的数学运算,只能执行基本的数学运算,而无需进一步分析或理解。这就是为什么椭圆曲线和椭圆曲线上的配对操作在密码学中变得重要的原因。
素域和扩展域
可以在椭圆曲线点上制作双线性映射- 即制作一个函数

其中P和Q是椭圆曲线点,结果是称为F_p^2的元素类型
首先,让我们了解素域和扩展域。
上图中的椭圆曲线之所以如此美丽,是因为该曲线的方程是使用普通实数定义的。
然而,在密码学中,使用传统的实数可能会导致使用对数“倒退” ,并破坏事物,因为存储和表示数字所需的空间量可以随意上涨。因此,我们在素数域中使用数字。
素数字段包括数字0、1、2…p-1 的集合,其中p 是素数,各种运算定义如下:

所有运算均以p 为模
Chia是一种特殊情况;通常,3/2 不是整数,现在我只想处理整数,所以我尝试找到数字x使得
x * 2 = 3 。
这可以使用扩展欧几里得算法来完成。例如,如果p = 7 ,则:

接下来我们要讲的是扩展字段。
您在数学书籍中经常遇到的一个常见示例是复数字段,其中实数字段通过附加元素sqrt(-1) = i进行“扩展”。
扩展字段的工作方式是采用现有字段,然后“添加”新元素并定义该新元素与原始字段中已有元素之间的关系(例如i² + 1 = 0 )。
重要的是这个方程对于原域中的任何数字都不成立,然后考虑原域中的元素和刚刚制作的新元素的所有线性组合。
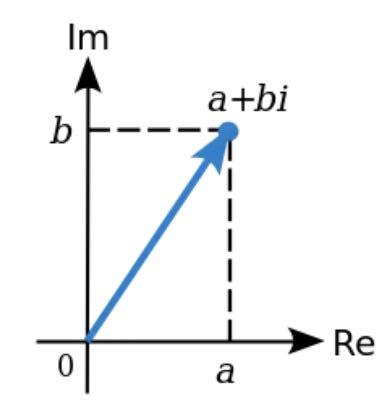
我们还可以扩展主要领域
例如,用 i扩展我们上面描述的素数域mod 7,我们可以执行以下操作:

如果您想查看代码中完成的所有数学运算,则素数字段和字段扩展都可以在此处完成
椭圆曲线配对
椭圆曲线配对是一种从两条椭圆曲线中获取两个点并将这些点映射为单个数字的机制。
您可以将此映射视为等效于椭圆曲线上的点相乘。
从数学上讲,椭圆曲线配对定义为将椭圆曲线上的两个点映射到另一个组(例如有限域)中的元素:
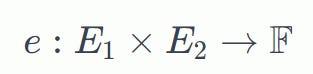
这里e是配对, E 1 和E 2 是椭圆曲线,𝐹 是有限域。
请注意,椭圆曲线E 1 和E 2 不需要不同。
一旦发生串联,结果是另一个组中的元素无法在下次串联中重用。
椭圆曲线配对具有称为双线性映射的某些属性:
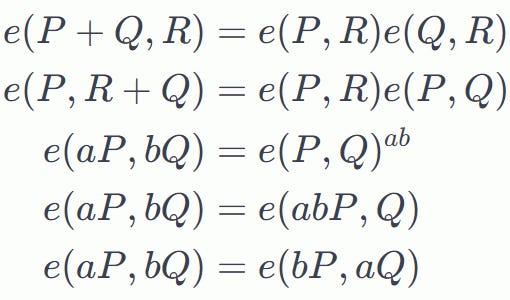
这里P 、 Q和R是椭圆曲线上的点, 𝑎ε𝑍,𝑏ε𝑍
通过使用这些“双线性映射” ,我们可以在这两条曲线上“移动”系数𝑎和𝑏 ,同时保持映射不变:
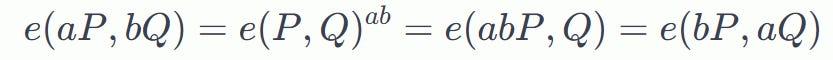
我们可以将椭圆曲线配对想象为G2 x G1 -> Gt的映射,其中:
G1是椭圆曲线,其中点满足形式方程
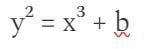
两个坐标都是F_p的元素(它们是简单的数字,但运算是对特定素数取模)
G2也是一条椭圆曲线,其中的点满足与G1相同的方程,但它们的坐标属于域F_p12 (我们定义一个新的“幻数” w ,由 12 次多项式定义,如下所示:

Gt是椭圆曲线的结果进入的对象类型。在我们考虑的曲线中, Gt是F_p^2 (与G2中使用的相同的强复数)
这里它必须满足双线性:
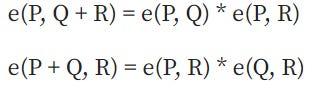
还有另外两个重要标准:
- 高效的可计算性:高效的计算能力意味着能够快速计算复合运算,并且不会太复杂。例如:如果我们简单地取点的离散对数并将它们相乘以制作一个复合值,这在计算上会变得太困难,就像破坏原始的椭圆曲线头一样。因此,如果可以有效地计算复合运算而不施加太多的计算负担,则该复合运算被认为是计算高效的。
- 非简并性:非简并性确保串联不是无用的串联,即它不只是返回独立于输入点的固定值。例如:如果我们将所有 P 和Q的耦合定义为e(P, Q) = 1 ,则这不会提供有关椭圆曲线上点之间关系的任何有用信息。因此,如果串联提供了有关输入点之间关系的有用信息,则该串联被认为是非退化的。
那么如何做到这一点呢?
首先,我们需要了解除数的概念,这是表示椭圆曲线上的点上的函数的另一种方式。
函数的除数本质上是计算函数的零数和无穷数。为了理解这意味着什么,让我们看一些例子。让我们修复一些点P = (P_x, P_y) ,并考虑以下函数:
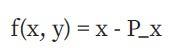
除数为[P] + [-P] – 2 * [O]
[P] + [Q]与[P + Q] 不同。原因如下:
- 该函数在P处为0,因为当x为P_x 时,因此x – P_x = 0。
- 该函数在-P处为0 ,因为-P和P具有相同的x坐标。
- 当x趋于无穷大时,函数趋于无穷大,所以我们说函数在O处是无穷大的。
原因在于椭圆曲线的方程:
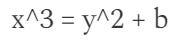
y上涨无穷大的速度大约比x快“1.5次”,以跟上x^3 的速度。因此,如果线性函数只有x ,则它将表示为 2 的倍数的无穷大,但如果函数有y ,则它将表示为 3 的倍数的无穷大。
现在,考虑一个“线函数” :
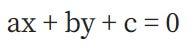
其中a、b和c经过精心选择,使得直线穿过椭圆曲线上的点P和Q。
由于椭圆曲线上的加法的工作方式,这也意味着它通过点-PQ 。该函数也会根据x和y趋于无穷大,从而Chia成为的可能性
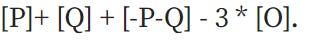

每个“有理函数” (在点坐标上仅使用有限数量的+、-、*、/运算定义的函数)唯一对应于一个divsor ,其条件是乘以一个常数(即,如果两个函数F和G有相同的除数,则F = G * k,其中k是常数)。
两个函数的Chia等于每个函数的Chia之和,因此

然后
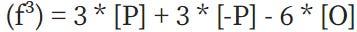
文章来源: Team Tech/Research Alphatrue
参考来源: