我們在此總結了首次對不活動洩漏進行理論分析的文章,該分析旨在在災難性網絡故障期間恢復最終確定性。這項工作已被 DSN2024 接受。
總結
- 不活動洩漏本質上對協議的安全性是有問題的。它有利於不斷完成區塊(活躍度),但代價是產生衝突的最終區塊(安全性)。
- 拜占庭驗證者(偏離協議的驗證者)的存在會加速安全性的喪失。
以太坊 PoS 區塊鏈致力於實現最終鏈的持續增長。因此,該協議激勵驗證者積極地完成區塊。不活動洩漏是用於重新獲得最終性的機制。具體來說,如果一條鏈連續四個時期沒有完成最終確定,就會引發不活動洩漏。不活動洩漏於 2023 年 5 月首次在主網上發生。
感謝 Ben Eddington 的出色工作(這激發了本文的創作),我們在這裡對不活動洩漏進行了很好的介紹。我們從不活動分數開始正式化不活動洩漏。
不活躍分數
在不活動洩漏期間,在時期t t ,驗證器i i的不活動分數I_i(t) I i ( t )為:
因此,如果驗證者處於不活躍狀態,其不活躍分數將增加4 4 ,如果處於活躍狀態,其不活躍分數將減少1 1。不活躍分數始終為正,並將用於在不活躍洩漏期間懲罰驗證者。
不活動懲罰
令s_i(t) s i ( t )表示驗證者i i在時期t t的質押,令I_i(t) I i ( t )表示其不活躍分數。每個時期t t 的懲罰為I_i(t-1)\cdot s_i(t-1)/2^{26} I i ( t − 1 ) ⋅ s i ( t − 1 ) / 2 26 。因此,質押的演變表示為:
不活動洩漏期間的質押
在本研究中,我們將權益函數s建模為連續可微函數,得到以下微分方程:
通過這個等式,我們可以通過固定其不活躍分數的演變來確定驗證者隨著時間的推移所獲得的權益。這正是我們所做的。我們定義了兩種類型的行為:活躍和不活躍。
- 活躍驗證者:他們始終處於活躍狀態。
- 不活躍的驗證者:他們總是處於不活躍狀態。
具有這些行為的驗證者的不活躍分數會經歷不同的演變:(a)活躍驗證者的不活躍分數為常數I(t)=0 I ( t ) = 0 ;(b)不活躍驗證者的不活躍分數每個時期增加 4, I(t)=4t I ( t ) = 4 t 。不活躍洩漏期間每種類型的驗證者的權益:
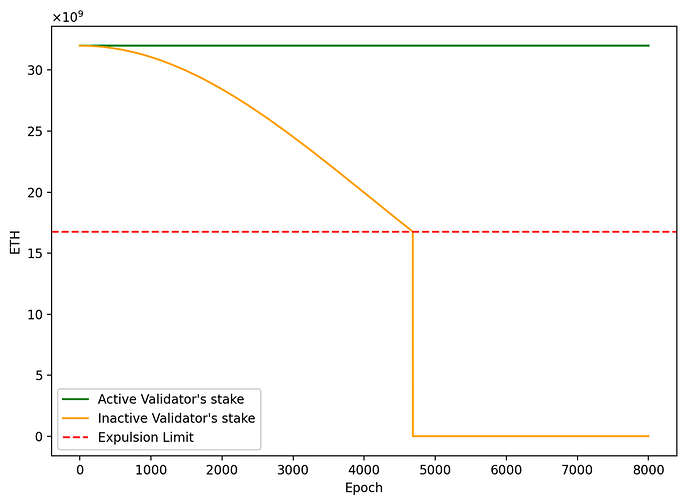
- 活躍驗證者的權益: s(t) = s_0 = 32. s ( t ) = s 0 = 32.
- 不活躍驗證者的權益: s(t) = s_0e^{-t^2/2^{25}}. s ( t ) = s 0 e − t 2 / 2 25 。
該圖顯示了驗證者在不活動洩漏期間根據其活動而變化的權益。協議設置了驅逐限制,以驅逐累積過多懲罰的驗證者。
什麼是活躍驗證者?
這是一個重要的細節;活動實際上取決於鏈。這意味著不同的鏈對同一驗證者將有不同的不活動分數。因此,驗證者可以從鏈中被逐出,而不會在另一條鏈上丟失 wei。
這是協議的形式化。現在我們對協議的安全性進行分析。為此,我們使用以下模型。
模型
- 網絡:我們假設一個部分同步系統,它在先驗未知的全局穩定時間(GST)之後從異步狀態轉換到同步狀態。
- 錯誤:驗證者要麼誠實,要麼拜占庭(偏離協議)。拜占庭驗證者可以任意偏離協議。
- 質押:每個驗證者初始質押 32 ETH。
異步狀態下消息傳輸延遲沒有限制。
安全出發
只有誠實的驗證者
根據構造,如果分區持續足夠長的時間,不活動洩漏將破壞安全性。問題是,速度有多快?
任何持續時間超過 4686 個 epoch(約 3 周)的網絡分區都將因最終確定衝突而導致安全性損失。這是在只有誠實驗證者的情況下,不活動洩漏持續時間的安全性上限。
詳細分析
讓我們分析一下驗證者(都是誠實的)被分成兩部分的場景。(根據我們的模型,我們處於異步狀態)。
分區必然會產生分叉,每個分區都建立在它們看到的唯一一條鏈上。一旦活躍驗證者的比例恢復到 2/3,鏈就會最終確定。
在這種情況下,通過了解驗證者在各個分區的分佈情況,我們可以計算出活躍驗證者的權益比例返回到每個分支上權益的 2/3 所需的時間,從而最終確定並打破安全性。
為了進行分析,我們做了以下標記。在不活動洩漏的開始:
- n n是驗證者的總數
- n_B n B是拜占庭驗證者的總數
- n_H n H是誠實驗證者的總數
- n_{H_1} n H 1是分支 1 上的誠實驗證者的數量
- n_{H_2} n H 2是分支 2 上的誠實驗證者的數量
在我們分析的第一部分中,沒有拜占庭驗證者,這意味著n=n_H n = n H 。誠實驗證者僅分為兩部分,因此n_H=n_{H_1}+n_{H_2} n H = n H 1 + n H 2 。
我們的目標是確定分支 1 上的誠實驗證者比例何時會超過總權益的 2/3。也就是說,我們查看以下比例:
優於 2/3。使用我們的符號,該比率可以重寫為:
s_{\text H_1} s H 1和s_{\text H_2} s H 2分別是誠實的活躍和非活躍驗證者的賭注。由於分支 1 上的n_{\text H_1} n H 1 個驗證者始終在分支 1 上活躍,而n_{\text H_2} n H 2 個驗證者始終在分支 1 上非活躍(它們在分支 2 上活躍);我們知道s_{\text H_1}(t)=s_0 s H 1 ( t ) = s 0和s_{\text H_2}(t)=s_0e^{-t^2/2^{25}} s H 2 ( t ) = s 0 e − t 2 / 2 25 。
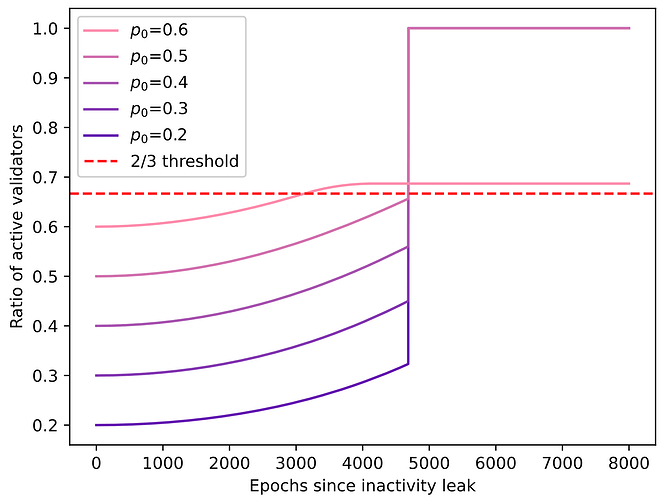
使用符號p_0=n_{\text H_1}/n_H p 0 = n H 1 / n H ,活躍驗證者隨時間的比例為:
此圖顯示了分支 1 上活躍驗證者隨時間的變化比例。如果到t= 4685時代還沒有完成,則非活躍驗證者將被剔除,從而導致活躍驗證者比例躍升至 100%。
拜占庭驗證者
我們現在添加了拜占庭驗證器。
這些拜占庭驗證器可以不受限制地向每個分區發送消息。
這看起來似乎有點過度,但這是分佈式系統中賦予拜占庭更多權力的傳統假設。提出 ETH2 協議的Gasper 論文在其模型中大量引用了PBFT 論文。以下是 PBFT 論文中的一句話: “我們允許一個非常強大的對手,它可以協調故障節點、延遲通信或延遲正確節點,以對複製服務造成最大的損害。”
我們的假設不太成立。想象一下歐洲和美國之間的通信被切斷,但每個地區內部的通信仍然正常的情況。根據我們的模型,我們假設拜占庭驗證者可以不受限制地與兩個地區進行通信,就好像他們有自己的跨地區通信方式一樣。
現在我們分析的情況是這樣的:
- 不到三分之一的股權由拜占庭驗證者持有( \beta_0=n_{\rm B}/n<1/3 β 0 = n B / n < 1 / 3 )。
- 誠實驗證者被分為分支1 1和2 2 ;分支1 1 上的比例為 p_0=n_{\rm H_1}/n_{\rm H} p 0 = n H 1 / n H ,分支 2 2 上的比例為 1 - p_0=n_{\rm H_2}/n_{\rm H} 1 − p 0 = n H 2 / n H 。
- 拜占庭驗證者可以與兩個分支進行通信。
拜占庭驗證者可以同時在兩個分支上活躍,從而更快地破壞安全性。分支 1 上的活躍驗證者比例為:
下表顯示了根據拜占庭驗證者的初始比例( \beta_0 β 0 )打破安全性所需的時間: 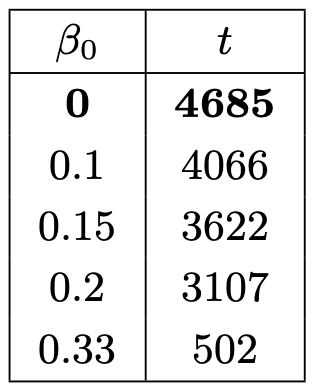
拜占庭驗證者可以加速安全性的喪失。如果他們的初始比例為 0.33,他們可以使衝突的最終確定發生速度比只有誠實參與者的場景快大約十倍。
原始論文提供了有關假設、場景、協議和其他方面的更多細節,例如:
- 拜占庭驗證者在不實施可削減行為的情況下破壞安全性的方法。
- 拜占庭驗證者在分叉的兩個分支上超過 1/3 閾值的方法。
- 考慮不活動洩漏時對概率彈跳攻擊的分析。劇透警告:這會稍微加劇攻擊,但攻擊開始和持續的條件使其不太可能成為真正的威脅。
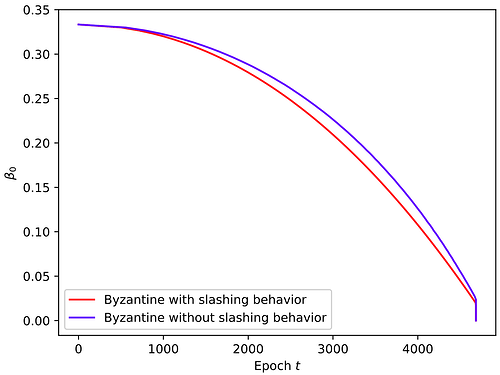
為了進一步快速瞭解該論文的研究結果,這裡有一張圖表,展示了拜占庭驗證者根據其初始比例以及其行為是否可削減而破壞安全性的速度。如您所見,即使沒有可削減行為,它們也會產生很大的影響。
結論
我們的研究結果強調了懲罰機制在拜占庭容錯 (BFT) 分析中的重要性。通過識別協議設計中的潛在問題,我們旨在為未來的改進提供見解,併為進一步調查提供工具。