撰文:mutourend & lynndell, Bitlayer Labs

1 引言
對於某個算法 f,兩個互不信任的參與方 Alice 和 Bob,可通過如下方式建立信任:
Alice 輸入 x,運行算法 f,獲得結果 y。Bob 基於相同的輸入 x,也運行算法 f,結果為 y′。如果 y = y′,則 Bob 認可 Alice 提供的輸入 x 和輸出 y。這是一種特殊的有效性證明機制,常用於區塊鏈共識。其中,Alice 為打包區塊的節點,Bob 為參與共識的節點。
Alice 輸入 x,對算法 f 運行 zk.prove 程序,獲得結果 y 和證明 proof。Bob 根據 f、y 和 proof,運行 zk.verify 程序。如果結果為 true,則 Bob 認可 Alice 的結果 y;如果結果為 false,則 Bob 不認可 Alice 的結果 y。這是有效性證明。其中,Bob 可以是鏈上合約。
Alice 輸入 x,運行算法 f,獲得結果 y。Bob 基於相同的輸入 x,也運行算法 f,結果為 y′。如果 y = y′,則什麼也不做;如果 y ≠ y′,則 Bob 對 Alice 發起挑戰,所挑戰的程序為 f。Alice 與 Bob 的交互次數可為一次或多次。根據挑戰響應流程來實現仲裁。這是欺詐證明。其中,Bob 為挑戰者,在鏈下監聽,在鏈上挑戰。
Alice 輸入 x,對算法 f 運行 zk.prove 程序,獲得結果 y 和證明 proof。Bob 根據 f、y 和 proof,運行 zk.verify 程序。如果結果為 true,則什麼也不做;如果結果為 false,則 Bob 對 Alice 發起挑戰,所挑戰的程序為 zk.verify。Alice 與 Bob 的交互次數可為一次或多次。Alice 與 Bob 的交互次數可為一次或多次。根據挑戰響應流程來實現仲裁。這是欺詐證明。其中,Bob 為挑戰者,在鏈下監聽,在鏈上挑戰。
對於以上 2,3,4,令 x 為 Layer2 交易和起始狀態,f 為 Layer2 共識程序,y 為交易結束狀態,則對應為區塊鏈 Layer2 擴容方案。其中:
有效性證明(Validity Proof):基於悲觀假設,必須證明有效後才接納,且即時生效。在有效性證明中,需提供 L2 狀態轉換正確的證據,反應了對世界的悲觀看法——當且僅當證明某狀態正確時,才會接納該狀態。
欺詐證明(Fraud Proof):基於樂觀假設,默認接納,除非有人證明有誤才拒絕。具有挑戰窗口期,挑戰窗口期過後才生效。在欺詐證明中,需提供 L2 狀態轉換不正確的證據,反應了對世界的樂觀看法——某狀態轉換默認是正確的,除非證明其不正確。
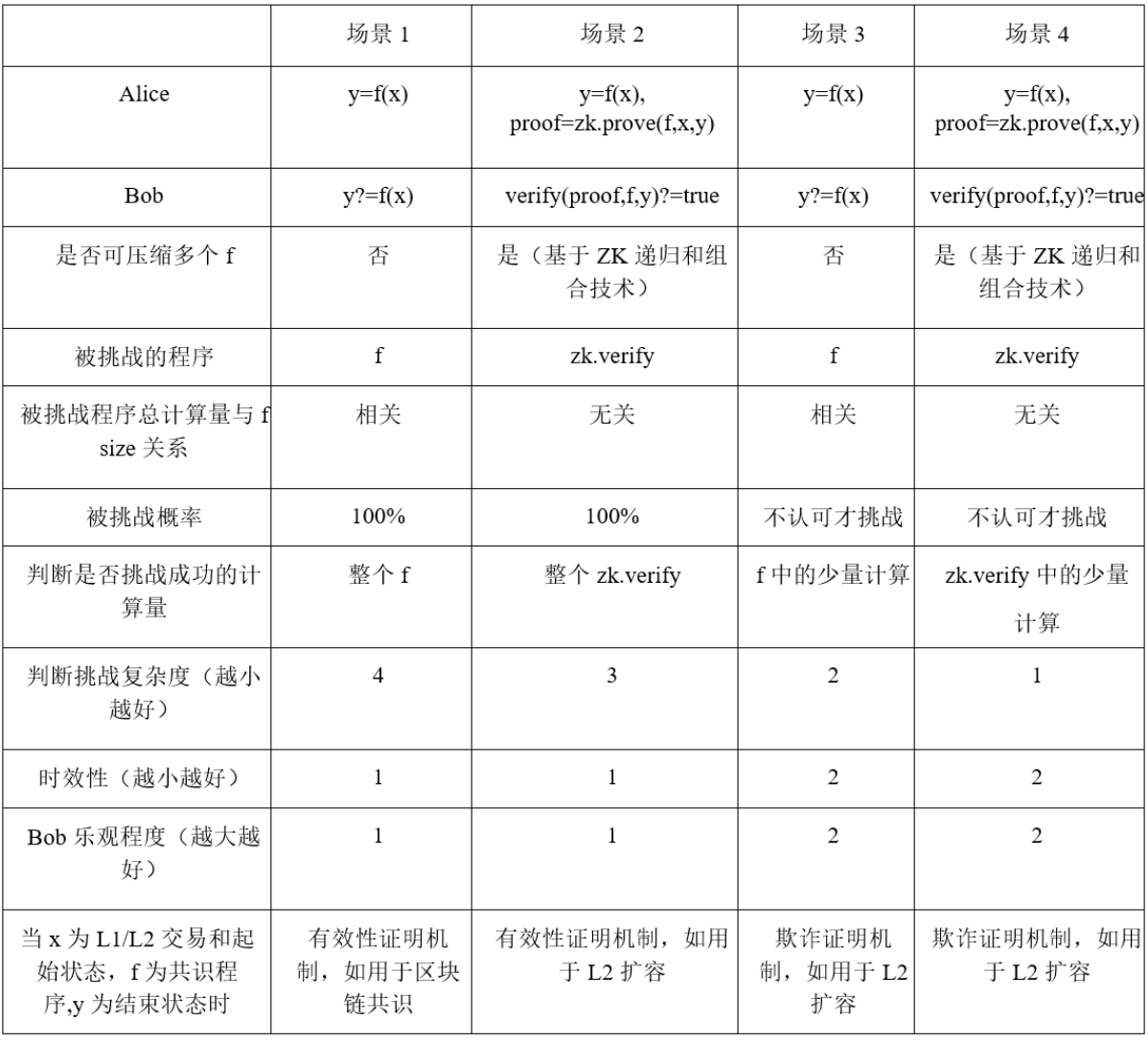
表 1: 信任建立方式
此外,需要注意:
區別欺詐證明和有效性證明的關鍵不是判斷是否使用了 SNARK/STARK 等 ZK 證明系統。ZK 證明系統所表達的是所用的證明方式,而欺詐還是有效性,則代表的是所證明的內容。這也是為何說表 1 中場景 1 所表示的為有效性證明。
有效性證明時效性更佳,但鏈上驗證複雜度相對高;欺詐證明鏈上驗證複雜度更低,但時效性相對差。
對於表 1 中 2 和 4 情況,藉助 ZK 遞歸和組合技術,可對多個 f 進行計算壓縮,大幅分攤降低鏈下計算在鏈上的驗證成本。
當前,受益於 solidity 圖靈完備智能合約,欺詐證明和有效性證明技術廣泛用於以太坊 Layer2 擴容。但是,在比特幣範式下,受限於比特幣有限的操作碼功能、1000 個 stack 元素等限制,這些技術應用仍處於探索階段。本文針對比特幣 Layer2 擴容場景下,總結了比特幣範式下的限制和突圍技術,研究有效性證明和欺詐證明技術,並梳理了比特幣範式下所獨有的腳本切分技術。
2 比特幣範式下的限制和突圍
比特幣範式下有諸多限制,但是能夠使用各種巧妙方法或技術來突破這些限制。例如,比特承諾可突破 UTXO 無狀態限制、taproot 可突破腳本空間限制、connector output 可突破 UTXO 花費方式限制、契約可突破預籤限制。
2.1 UTXO 模型與腳本限制
比特幣採用 UTXO 模型,每個 UTXO 都鎖定在 locking 腳本中,該腳本定義了花費該 UTXO 所必須滿足的條件。比特幣腳本具有如下侷限性:
比特幣腳本是無狀態的;
對於 P2TR 輸出類型,單筆交易中可容納的操作碼總數最多約為 400 萬個,會填滿整個區塊,而對於其他輸出類型則僅有 1 萬個操作碼;
單個 UTXO 的花費方式有限,缺少組合花費方式的探索;
不支持靈活的契約功能;
棧大小最多限制為 1000 個元素(altstack + stack),且單個元素最大 size 為 520 字節;
算術運算(如加法、減法)僅限於 4 字節元素。無法修改為長元素,如 20 字節或更大的元素,但這是密碼學運算所必需的;
OP_MUL 和 OP_CAT 等操作碼均已被禁用,若使用現有操作碼進行模擬,成本極高,如模擬 one-round BLAKE3 哈希,script size 約為 75K。
2.2 比特承諾:突破 UTXO 無狀態限制
當前比特幣腳本是完全無狀態的。當執行比特幣腳本時,其執行環境在每個腳本之後都會被重置。這導致比特幣腳本無法原生支持約束腳本 1 和腳本 2 擁有相同的 x 值。但是,可通過一些方法來繞過該問題,其核心思想是以某種方式對一個值進行簽名。如果可對一個值創建簽名,則能夠實現有狀態的比特幣腳本。即需通過在腳本 1 和腳本 2 中檢查 x 值的簽名,就可強制腳本 1 和腳本 2 中使用相同的 x 值。如果存在衝突簽名,即對同一變量 x 簽署了 2 個不同的值,則可對其進行懲罰。該解決方案即為 bit commitment(比特承諾)。
Bit commitment 的原理相對簡單。所謂 bit,是指對待簽名消息中的每個 bit,設置 2 個不同的哈希值,即 hash0 和 hash1。如果需要簽署的 bit 值為 0,則揭露 hash0 的原像 preimage0;如果需要簽署的 bit 值為 1,則揭露 hash1 的原像 preimage1。
以單個 bit 消息 m ∈{0,1}為例,相應的 bit commitment 解鎖腳本只是一些原像:如果該 bit 值為 0,則對應的解鎖腳本為 preimage0——「0xfa7fa5b1dea37d71a0b841967f6a3b119dbea140」;如果該 bit 值為 1,則相應的解鎖腳本為 preimage1——「0x47c31e611a3bd2f3a7a42207613046703fa27496」。因此,藉助 bit commitment,可突破 UTXO 無狀態限制,實現有狀態的比特幣腳本,從而使得各種有趣的新特性變得可能。
OP_HASH160
OP_DUP
<0xf592e757267b7f307324f1e78b34472f8b6f46f3> // This is hash1
OP_EQUAL
OP_DUP
OP_ROT
<0x100b9f19ebd537fdc371fa1367d7ccc802dc2524> // This is hash0
OP_EQUAL
OP_BOOLOR
OP_VERIFY
// Now the value of the bit commitment is on the stack. Either ”0” or ”1”.
比特承諾目前有 2 種實現方式:
Lamport 一次性簽名:原理相對簡單,僅需要使用哈希函數,所以是比特幣友好的。對於消息中的每一位,均需要承諾 2 個哈希值,導致簽名數據相對較大。換言之,對於一個長度為 v bits 的消息,公鑰長度為 2v bits,簽名長度為 v bits。
Winternitz 一次性簽名:相比於 Lamport 簽名,可大幅降低簽名和公鑰長度,但是增加了簽署和驗籤複雜度。該方案可靈活設置不同的 hash chain 長度 d 值,從而在長度和複雜度方面進行權衡。例如,設置 d =15 時,則公鑰長度和簽名長度均要短約 4 倍,但是驗籤複雜度將提高 4 倍。這本質上是在比特幣棧空間和 script size 之間的取捨。Lamport 簽名可視為 Winternitz 簽名中 d =1 時的特例。
目前,BitVM2 庫中,基於 Blake3 的哈希函數實現了 Winternitz 簽名。單個 bit 對應的簽名長度約為 26 字節。由此可知,通過 bit commitment 來引入狀態,成本是昂貴的。因此,在 BitVM2 工程實現中,首先對消息進行哈希運算獲得 256bit 的哈希值,然後再對哈希值進行 bit commitment,從而節約開銷,而不是直接對原始較長的消息的每個 bit 進行承諾。
2.3 Taproot:突破腳本空間限制
自 2021 年 11 月激活的比特幣 Taproot 軟分叉升級中包含 3 個提案:Schnorr 簽名(BIP 340),Taproot (BIP 341)和 TapScript(BIP 342)。引入了一種新的交易類型——Pay-to-Taproot(P2TR)交易。P2TR 交易通過結合 Taproot、MAST(默克爾抽象語法樹)和 Schnorr 簽名的優點,可創建更私密、靈活和可擴展的交易格式。
P2TR 支持兩種花費方式:根據 key path 或 script path 實現花費。
根據 Taproot(BIP 341)中的規定,當按 script path 花費時,對應的 Merkle path 最大長度不超過 128。這意味著 taptree 中 tapleaf 個數不超過 2128 個。自 2017 年 segwit 升級以來,比特幣網絡以 weight units 來衡量區塊大小,最大支持 400 萬 weight units(即約 4MB)。某 P2TR output 通過 script path 被花費時,實際只需要揭露某單個 tapleaf 腳本,即區塊打包的為單個 tapleaf 腳本。這意味著,對於 P2TR 交易,對應每個 tapleaf 的腳本 size 最大約為 4MB。不過比特幣默認策略中,許多節點只轉發小於 400K 的交易,更大的交易若想被打包,則需跟礦工合作。
Taproot 所帶來的腳本空間溢價,使得用現有 opcode 模擬乘法、哈希等密碼學運算更具價值。
當基於 P2TR 構建可驗證計算時,所對應的 script size 可不再受限於 4MB 的限制,而是可將該計算切分為多個子函數,將其分佈在多個 tapleaf 上,從而突破 4MB 的腳本空間限制。事實上,當前 BitVM2 中所實現的 Groth16 verifier 算法,其 size 高達 2GB。但是,能夠對其切分並分佈在約 1000 個 tapleaf 中,通過與 bit commitment 結合使用,可通過約束各子函數輸入輸出之間的一致性,約束整個計算的完整性和正確性。
2.4 Connector output:突破 UTXO 花費方式限制
比特幣目前提供的單個 UTXO 原生花費方式有:按腳本花費,或按公鑰花費。因此,只要提供了對應正確的公鑰簽名或滿足腳本條件,則能夠花費該 UTXO。兩個 UTXO 是可獨立花費的,不能添加限定措施以約束兩個 UTXO,使得需滿足一些額外條件才可被花費。
但是,Ark 協議的創始人 Burak,通過巧妙藉助 SIGHASH flag,實現了 connector output。具體而言,Alice 可創建一個簽名,將其 BTC 發送給 Bob。但是,由於簽名可對多個 Inputs 進行 commit,Alice 可設置其簽名是有條件的:該簽名對 Take_tx 交易是有效的,當且僅當該交易消耗了第二個 input。第二個 input 就稱為 connector,連接了 UTXO A 和 UTXO B。換言之,Take_tx 交易有效,當且僅當 UTXO B 未被 Challenge_tx 花費掉。因此,通過銷燬 connector output,即可阻斷 Take_tx 交易生效。
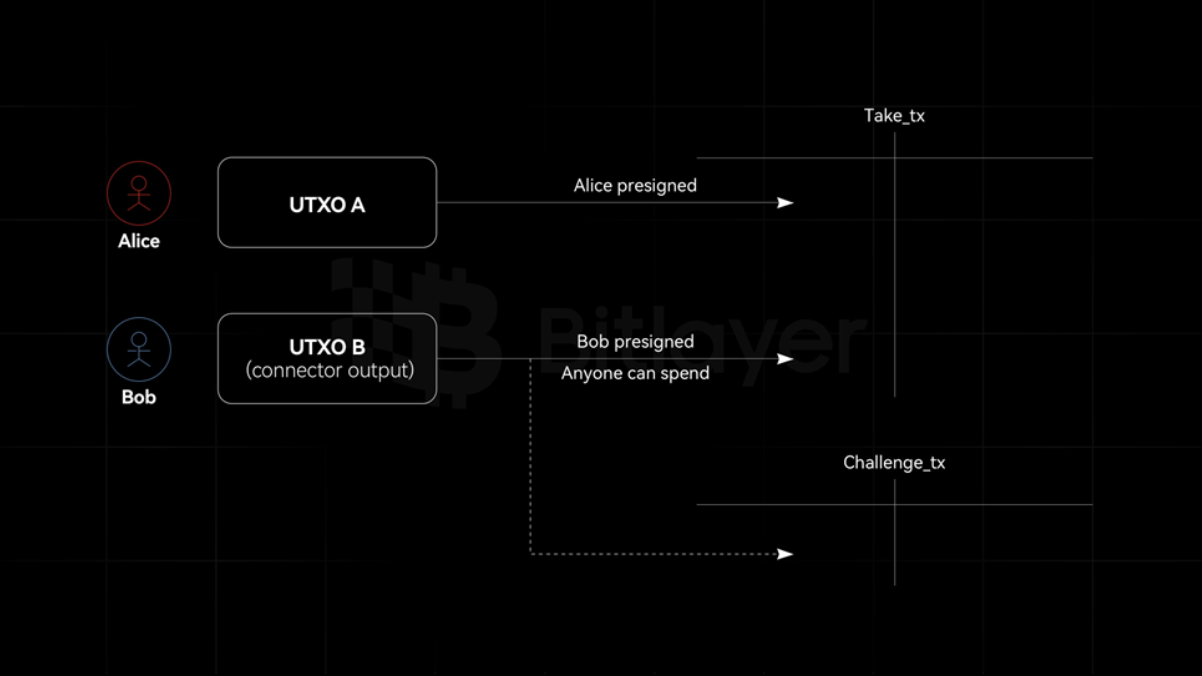
圖 1: connector output 示意
在 BitVM2 協議中,connector output 充當 if...else 功能。一旦 connector output 被某交易花費,就不能被另一筆交易花費,以確保其獨佔性花費。在實際部署中,為預留挑戰響應週期,額外引入了具有 timelock 的 UTXO。此外,相應的 connector output 也可根據需要設置不同的花費策略,如對挑戰交易可設置為任何人可花費,而對響應交易可設置為僅 operator 可花費或超期後任何人可花費。
2.5 契約:突破預籤限制
目前比特幣腳本主要限制瞭解鎖的條件,而沒有限制該 UTXO 如何進一步被花費。其原因在於比特幣腳本無法讀取交易自身的內容,即無法實現交易自省。如果比特幣腳本能夠檢查交易的任何內容(包括 output),就可實現契約功能。
當前的契約實現方式可分為兩類:
預籤:基於現有比特幣腳本能力,通過預籤構建功能有限的預先確定的契約。即提前設計和簽署所有可能的未來交易,將參與方鎖定在特定的私鑰和費率中。一些方案甚至要求參與方生成用於所有預簽名交易的短期私鑰。當預簽完成後,則安全地刪除這些短期私鑰,使得攻擊者無法獲得短期私鑰,從而盜走資金。但是,每次新增參與方,或更新操作時,均需要重複以上過程,導致維護成本繁重。例如,閃電網絡通過預籤實現了 2 方契約,並藉助哈希時間鎖(HTLC)技術,實現了多個 2 方契約的路由功能,從而實現信任最小化的擴容策略。但是,閃電網絡需預籤多筆交易,且僅限於兩方,略顯笨重;在 BitVM1 中,每次初始化時均需要預籤數百筆交易,而優化後的 BitVM2 中,每次初始化時需要預籤的交易數也達數十筆。無論是 BitVM1 還是 BitVM2,只有參與預籤的 operator,才有資格進行報銷。如果有 n 個參與方參與預籤,每個參與方需預籤 m 筆交易,則每個參與方的預籤複雜度將為 n ∗ m。
引入契約操作碼:引入新的契約功能操作碼,可大幅降低契約參與方之間的通信複雜度和維護成本,從而為比特幣引入更靈活的契約實現方式。例如,OP_CAT:用於拼接字節字符串。儘管其功能非常簡單,但是功能非常強大,能夠大幅降低 BitVM 複雜度;OP_TXHASH:能夠以更好的粒度控制契約內的動作。如果在 BitVM 中使用,則能夠支持更大的 operator 集合,從而大幅改進 BitVM 的安全假設,讓其信任最小化。此外,預籤方式註定了 BitVM 設計中,operator 只能採用墊付報銷流程,資金利用效率較低;而通過新的契約操作碼,有可能實現直接從 peg-in 資金池付款給出金用戶,進一步提高資金效率。因此,靈活的契約模式,將有效突破傳統預籤限制。
3 比特幣 Layer2 擴容:有效性證明與欺詐證明
有效性證明與欺詐證明均可用於比特幣 L2 擴容,二者的主要區別如表 2 所示。
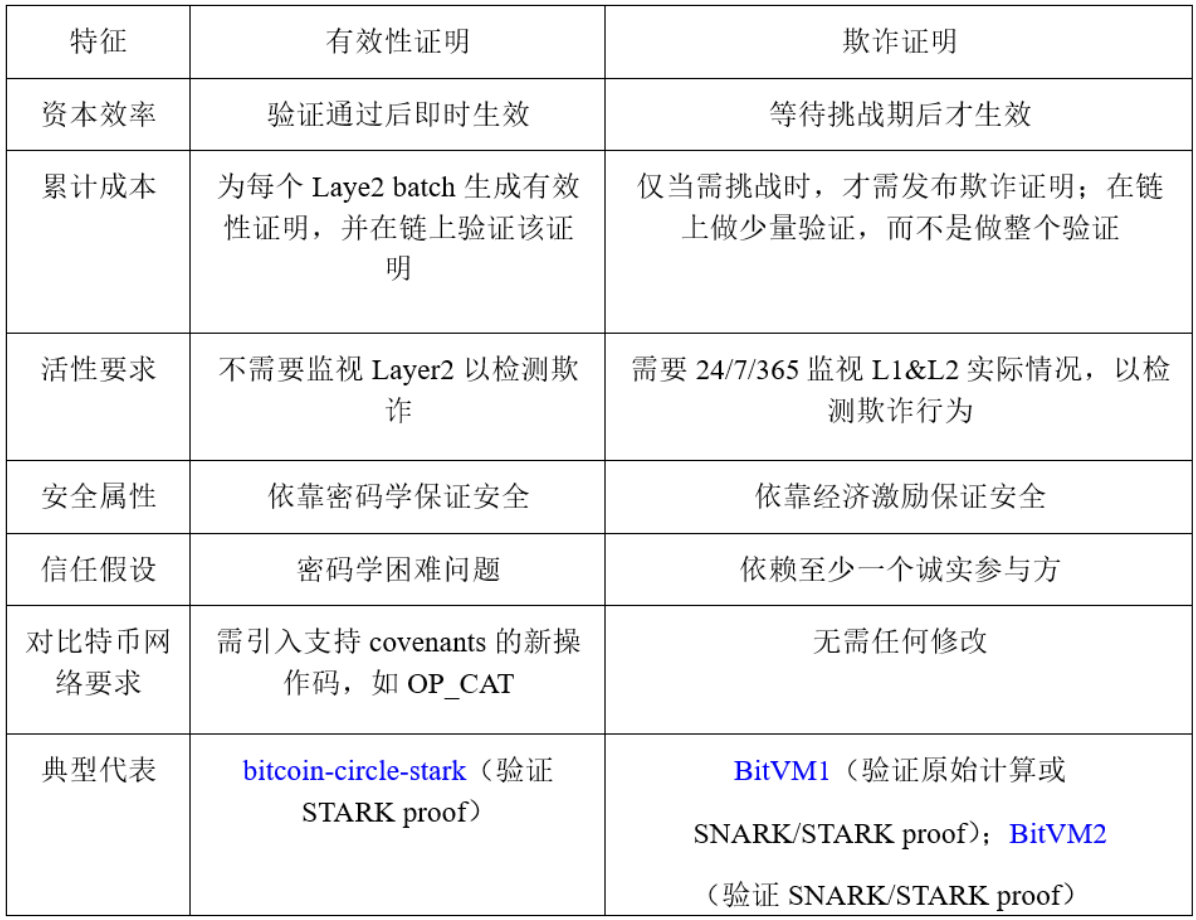
表 2: 有效性證明與欺詐證明
基於比特承諾、taproot、預籤和 connector output,可構建基於比特幣的欺詐證明。基於 taproot,同時通過引入契約操作碼,如 OP_CAT,可構建基於比特幣的有效性證明。此外,根據 Bob 是否有準入制度,欺詐證明可分為許可式欺詐證明和無需許可式欺詐證明。其中,許可式欺詐證明中,僅特定群體才能作為 Bob 發起挑戰,而無需許可式欺詐證明中,任意第三方均可作為 Bob 發起挑戰。無需許可式的安全性要優於許可式,可降低各許可參與方竄謀作惡的風險。
根據 Alice 和 Bob 挑戰響應交互的次數,欺詐證明可分為一輪欺詐證明和多輪欺詐證明,如圖 2 所示。
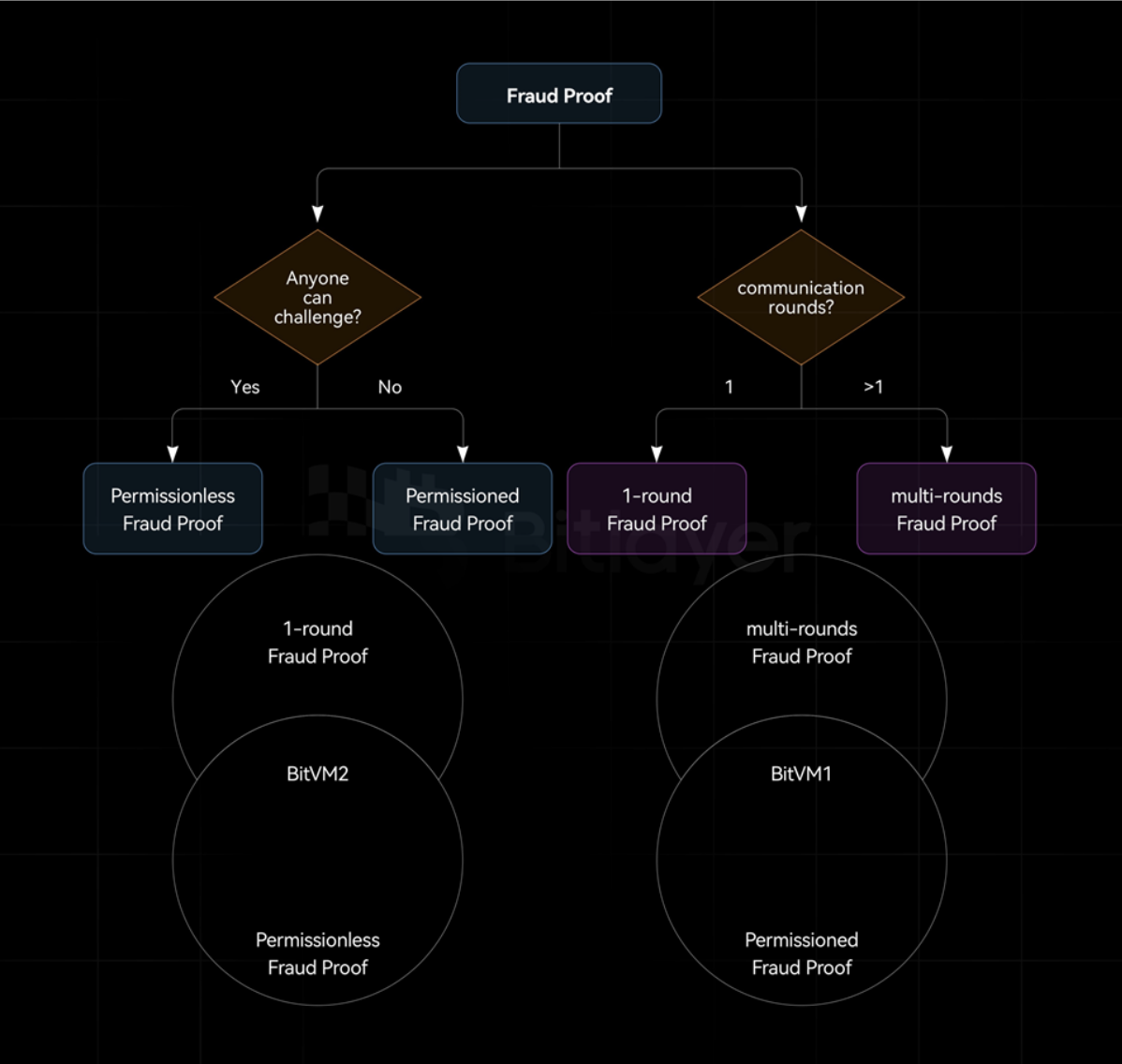
圖 2: 一輪欺詐證明與多輪欺詐證明
如表 3 所示,欺詐證明可以通過不同的交互模型來實現,包括一輪交互模型和多輪交互模型。
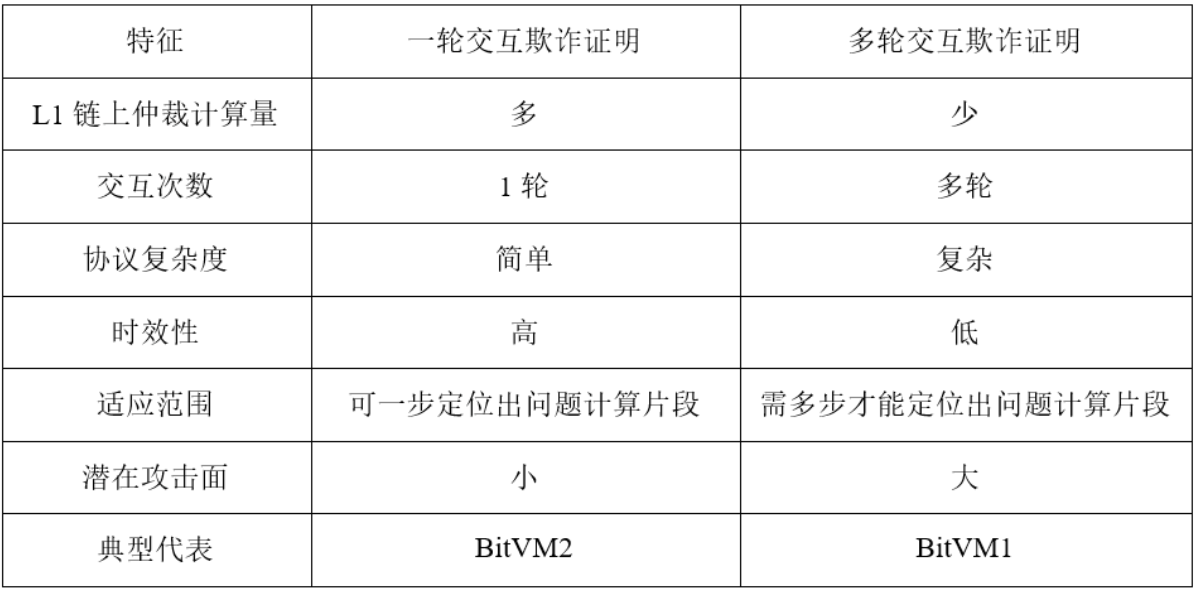
表 3: 一輪交互與多輪交互
在比特幣 Layer2 擴容範式下,BitVM1 採用多輪欺詐證明機制,BitVM2 採用一輪欺詐證明機制,bitcoincircle stark 採用有效性證明。其中,BitVM1 和 BitVM2 可在不對比特幣協議做任何修改的情況下實施,而 bitcoin-circle stark 需要引入新的操作碼 OP_CAT。
對於大多數計算任務,比特幣 signet,testnet 和 mainnet 均無法以 4MB 的腳本來完整表示,需要使用腳本 Split 技術——即將表達完整計算的腳本,切分為小於 4MB 的 chunk,分佈到各個 tapleaf 中。
3.1 比特幣上的多輪欺詐證明
如表 3 中所示,多輪欺詐證明適於希望降低鏈上仲裁計算量,和(或)無法一步定位出問題計算片段的場景。多輪欺詐證明,顧名思義,證明者和驗證者之間,需要多輪交互以定位出問題計算片段,然後再基於所定位出的計算片段進行仲裁。
Robin Linus 早期的 BitVM 白皮書(通常稱為 BitVM1),使用的多輪欺詐證明。假設每輪挑戰期為一週,採用二分查找法定位問題計算片段,則對 Groth16 Verifier 的鏈上挑戰響應週期將高達 30 周,時效性極差。儘管當前有團隊在研究比二分法更高效的 n-ary 查找法,但相比於一輪欺詐證明中的 2 週週期,其時效性仍低很多。
目前,比特幣範式下的多輪欺詐證明均採用許可式挑戰,而一輪欺詐證明實現了無需許可式挑戰方式,降低了參與方串謀風險,從而安全性更高。為此,Robin Linus 充分利用了 taproot 的優勢,對 BitVM1 進行優化。不僅將交互輪次降低至 1 輪,還將挑戰方式擴展為無需許可式,但是其代價是增加了鏈上仲裁計算量。
3.2 比特幣上的一輪欺詐證明
在證明者和驗證者之間僅通過一次交互,即可完成驗證欺詐證明。該模型中,驗證者僅需發起一次挑戰,證明者只需做一次響應。在該響應中證明者需提供一個證據,聲稱其計算是正確的。如果驗證者能夠從該證據中找出不一致性,則挑戰成功,否則挑戰失敗。一輪交互欺詐證明的特點如表 3 所示。
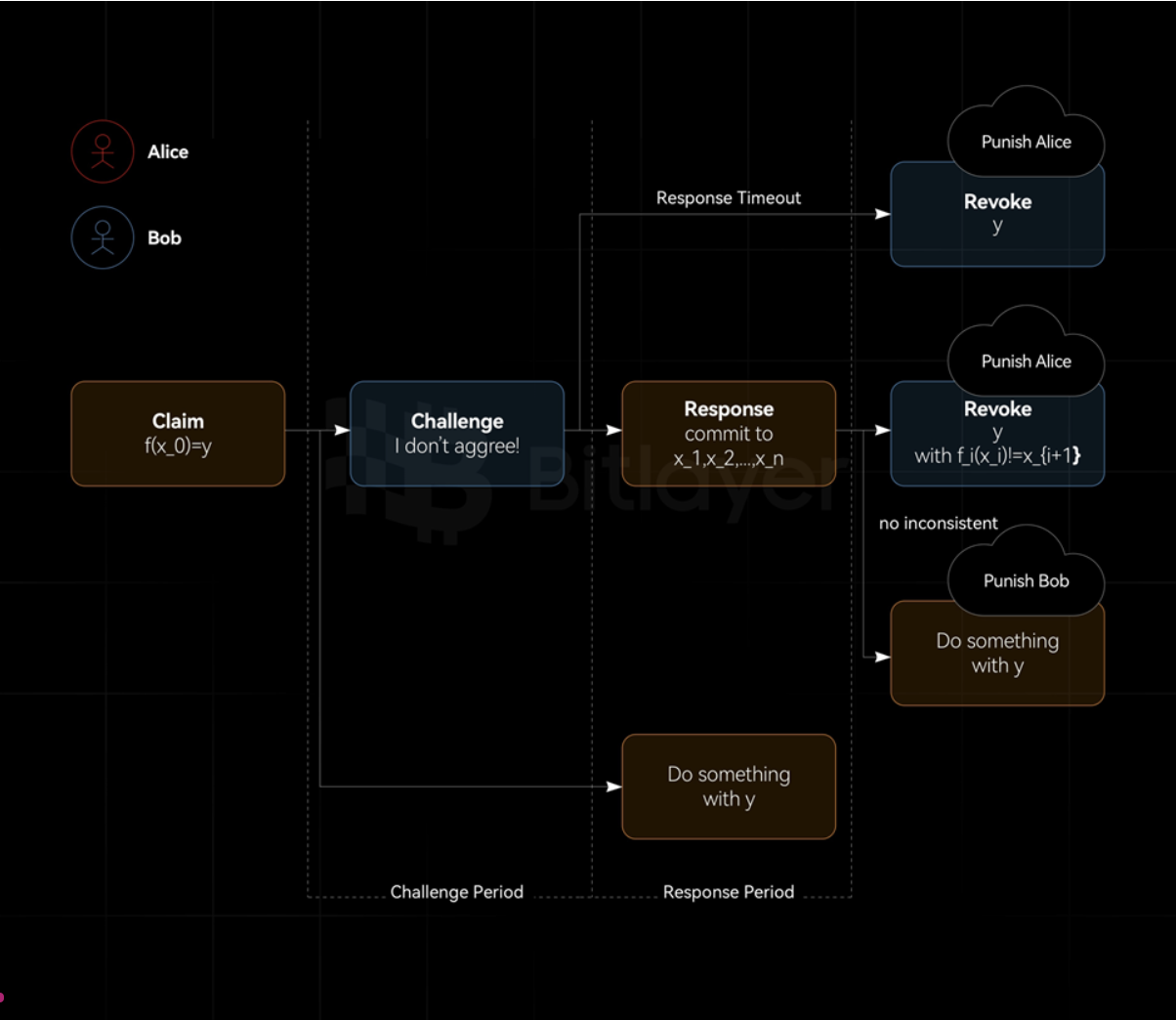
圖 3: 一輪欺詐證明
Robin Linus 2024 年 8 月 15 日發佈了 BitVM2: Bridging Bitcoin to Second Layers 技術白皮書中,採用類似圖 3 的方式,以一輪欺詐證明方式,實現了 BitVM2 跨鏈橋。
3.3 比特幣 +OP_CAT 實現有效性證明
OP_CAT 是比特幣最初發布時腳本語言的一部分,因安全漏洞問題在 2010 年被禁用。但是,數年來,比特幣社區一直在討論將其激活。目前 OP_CAT 已被分配編號 347 且已在比特幣 signet 上啟用。
OP_CAT 主要功能是將堆棧中的兩個元素結合起來,並將合併後的結果推回堆棧。這個功能特性,開啟了比特幣上的契約和 STARK Verifier:
契約:Andrew Poelstra 提出 CAT and Schnorr Tricks I,使用 OP_CAT 和 Schnorr 技巧在比特幣上實現契約。其中,Schnorr 算法是 P2TR 輸出類型的數字簽名;對於其他輸出類型,可以使用類似的 ECDSA 技巧,見 Covenants with CAT and ECDSA。藉助 OP_CAT 契約,可協助將 STARK Verifier 算法拆分為多筆交易,逐步驗證整個 STARK proof。
STARK Verifier:STARK Verifier 本質上是將數據連接在一起並對其進行哈希運算。與代數運算不同,哈希運算是一種原生比特幣腳本操作,可以節省大量開銷。以 OP_SHA256 為例,原生方式僅為一個操作碼,而模擬方式則需要數百 K 個。STARK 中的主要哈希運算是 Merkle 路徑的驗證和 Fiat-Shamir 變換。因此,OP_CAT 對 STARK Verifier 算法非常友好。
3.4 比特幣腳本 Split 技術
儘管經 SNARK/STARK 證明後,運行相應 verifier 算法驗證 proof 所需的計算量要遠小於直接運行原始計算 f 所需的計算量。但是,將其轉換為以比特幣腳本實現 verifier 算法時,所需的腳本量仍然是巨大的。當前,基於現有比特幣操作碼,經優化後,所實現 Groth16 verifier 腳本 size 和 Fflonk verifier 腳本 size 仍均大於 2GB。然而,比特幣單個區塊 size 僅為 4MB,無法在單個區塊內運行整個 verifier 腳本。但是,比特幣自 taproot 升級後,支持按 tapleaf 執行腳本,可將 verifier 腳本切分為多個 chunks,然後以每個 chunk 為 tapleaf,構建 taptree。各個 chunk 之間,藉助 bit commitment 來保證 chunk 之間值的一致性。
在有 OP_CAT 契約情況下,可將 STARK Verifier 拆分為多筆小於 400KB 的標準交易,從而可在無需與礦工協作的情況下,完成整個 STARK 有效性證明的驗證。
本節,重點關注的是未引入激活任何新操作碼的現有情況下,比特幣腳本的相關 Split 技術。
當進行腳本切分時,需平衡如下維度信息:
單個 chunk script size 不超過 4MB,需包含 input bit commitment 腳本、交易簽名等空間。
單個 chunk stack size 最大不超過 1000。所以應讓各個 chunk stack 上僅保留所需的元素,從而預留足夠的 stack 空間來為 script size 優化服務。因為比特幣交易手續費不取決於所用 stack size。
比特幣上的 bit commitment 是昂貴的。所以當前 1 個 bit 對應 26 字節,應讓相鄰 2 個 chunk 間的輸入輸出的 bits 數量最小化。
為便於審計,每個 chunk 的功能應儘可能明確。
當前,腳本的切分方式主要分為以下 3 大類:
自動切分:根據 stack size 和 script size,尋找 script size 為 3MB 左右而 stack size 最小的切分方式。這種方式的優點在於:與具體的 verifier 算法無關,可擴展為任意計算的腳本切分。缺點在於:(1)需單獨標記整塊邏輯,如 OP_IF 代碼塊不可被切分,否則切分後的腳本執行結果將不正確;(2)chunk 執行結果可能對應 stack 上的多個元素,需根據實際計算邏輯來標記需應用 bit commitment 的棧元素個數;(3)每個 chunk 腳本所實現邏輯功能可讀性差,不利於審計;(4)stack 上可能包含下一 chunk 不需使用的元素,浪費棧空間。
功能性切分:根據計算中的各個功能子函數來切分,子函數的輸入輸出值明確,在腳本切分的同時,也實現了各個 chunk 所需的 bit commitment 腳本,使最終的 chunk 總腳本 size 小於 4MB,stack size 小於 1000 即可。優點在於:功能清晰,單個 chunk 邏輯明確,可讀性好,便於審計。缺點在於:原始計算邏輯的表達,與腳本級邏輯的表達,是不匹配的,原始計算子函數可能最優,並不代表腳本級最優。
人工切分:腳本切分點不在於功能子函數,而是人工設置切分點。尤其適合於單個子函數 size 大於 4MB 的情況。優點在於:可對 heavy script size 子函數,如 Fq12 相關計算子函數進行人工切分;單個 chunk 邏輯明確,可讀性好,便於審計。缺點在於:受限於人工調優能力,當總體腳本做了優化後,之前設置的各個人工切分點可能不是最優,需重新調整。
例如,Groth16 verifier 經過多輪優化,其 script size 由約 7GB 降低至約 1.26GB。除做這種總體計算優化外,還可對各個 chunk 單獨優化,以充分利用 stack 空間。如可通過引入更優的基於 lookup table 的算法,並對 lookup table 進行動態加載卸載,可進一步降低每個 chunk 的 script size。
web2 編程語言計算成本和運行環境,與比特幣腳本成本和運行環境完全不同,所以對於各種算法的比特幣腳本實現,僅翻譯現有實現是行不通的。因此,需針對比特幣場景,考慮以下優化:
尋找內存局部性最優的算法,哪怕犧牲部分計算量,可降低 chunk 間輸入輸出 bits 數,從而降低 BitVM2 設計中的 assertTx 交易所需承諾的數據量。
利用相關運算(如邏輯運算)的可交換性,x&y = y&x,節約幾乎一半的查找表。
當前,Fq12 運算對應的腳本量很大,可考慮藉助 Fiat-Shamir、Schwartz-Zipple 和多項式承諾方案,大幅降低 Fq12 擴域運算的計算複雜度。
4 小結
本文首先介紹了比特幣腳本限制,並介紹使用比特幣承諾突破 UTXO 無狀態限制、使用 Taproot 突破腳本空間限制、使用 connector output 突破 UTXO 花費方式限制,使用契約突破預籤限制。然後對欺詐證明和有效性證明的特點、許可式欺詐證明和無需許可式欺詐證明的特點、一輪欺詐證明和多輪欺詐證明的特點、比特幣腳本切分技術進行了全面的梳理和總結。








