機構:KuCoin
1 引言
許多加密貨幣交易所採用了複雜的風險管理措施,以防止清算風險。這些措施包括設置多層次的風險限額以及限制高槓杆的使用。此外,交易所會根據基礎資產的價格和市場流動性動態調整風險限額和保證金比率等參數。然而,這些流程不僅複雜,而且缺乏明確的管理標準,需要投入大量資源來維護一個可能存在內部不自洽的系統 — — 例如,增加資金並不一定能帶來更大的頭寸規模,因為槓桿級別可能會突然變化。
在某些交易平臺上(見圖 1),存在近百個風險限額級別。這些被動的級別變化增加了系統管理的複雜性,並可能導致部分強制平倉,從而損害用戶的利益。
我們的目標是開發一個非線性模型,以模擬在給定資金下的合理頭寸規模,從而實現更靈活和高效的風險管理。此方法涉及重構內部公式體系,以實現自洽性,為現有複雜的風險限額模板提供一個可行的替代方案。
本文提出了一種新的風險管理框架,用以取代現有的限額模型。該方法已在 KuCoin 的全倉系統中實施,表現出一些明顯的優勢:
1. 更接近傳統交易所的頭寸管理設置,使機構資本更容易適應。
2. 不需要根據頭寸規模或槓桿使用情況來調整風險限額。
3. 簡化了操作流程,減少了交易所的負擔,同時降低了為保護交易所自身利益而損害用戶利益的風險。
該模型為風險管理提供了一種更加透明且簡化的方式,使交易所的運營與用戶利益更加一致。
2 模型
2.1 最大頭寸規模
假設用戶賬戶持有資金量為 C ,基礎資產的期貨合約價格為 p 。初始保證金率 r 對應於用戶選擇的槓桿的倒數。在忽略交易費用的情況下,用戶可以開設的合約數量為:

然而,當資金 C 過大或保證金率r過低時,對交易所帶來的風險會顯著增加。因此,當 C 和 r 固定且 C 較大時,交易所的風險分級制度會限制允許的最大頭寸,通常遠低於 C/(p*r)。反之,對於較小的資金 C,頭寸規模則更接近於 C/(p*r)。
許多交易所採用幾十到上百個風險級別來管理這種關係。因此,隨著用戶資金的增長,用戶常常需要調整其所在的風險級別。此類限制的目的可通過以下對數函數大致表達:
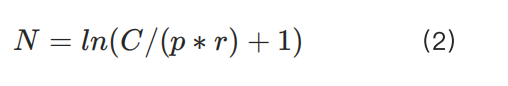
顯然,當 C 較大時,對數函數的一階導數減小,意味著可實現的頭寸規模將小於線性公式計算的結果。然而,這提出了一個挑戰:為了近似成立 ln (x+1)≈x ,C 必須足夠小,且 p 必須足夠大。否則,即使 C 較小,用戶仍可能無法實現理論上的最大頭寸 C/(p*r)。
為解決這一問題,我們需要根據不同合約類型的特徵引入更大的縮放參數 k,將原公式修改為:
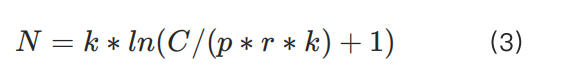
此調整滿足了小額資金用戶的需求,同時也符合大額資金用戶的風險控制要求。
在 KuCoin 的全倉系統中,考慮到已開倉位和其他保證金要求,我們定義如下變量:
•F:其他合約和未成交訂單所佔用的保證金。
•E:用戶期貨賬戶中的總權益。
•Q:與新訂單方向一致的待定訂單的頭寸規模。
•O:當前已開頭寸規模(如果與新訂單方向一致則為正值,反之為負值)。
最大允許頭寸的計算公式為:
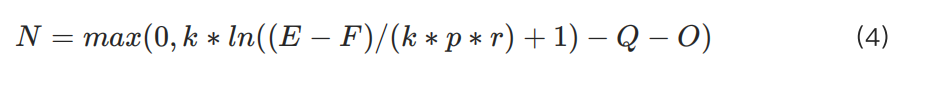
因此,在 KuCoin 的此模型下,對於典型資金規模,槓桿與最大允許頭寸的關係可表示為如下圖表:
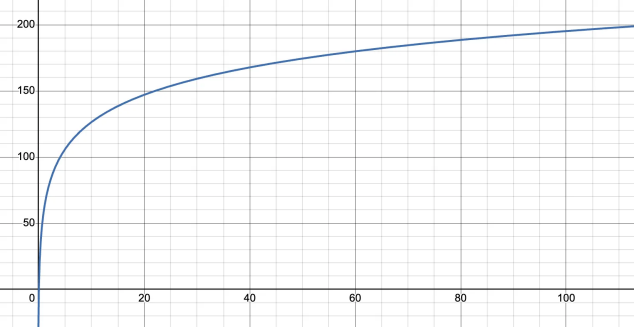
該圖展示了模型如何在非線性保證金調整的幫助下,實現規模和穩定性的平衡,既滿足小額用戶最大化頭寸的需求,又保障大額用戶的風險控制。
然而,在大多數交易所(如 OKX 和 Binance)上,槓桿與頭寸規模的關係通常表現為一種扭曲的曲線:
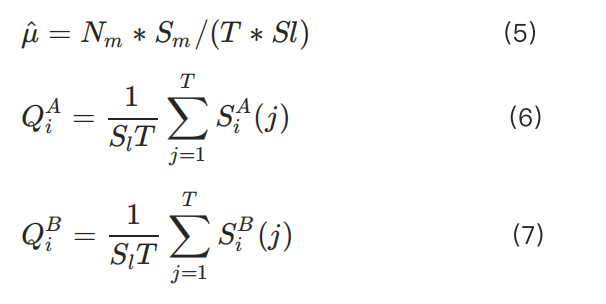
事實上,即使是 MMR(維持保證金率)也呈現出類似的模式。這對大額資金用戶尤為具挑戰性。例如,當 IMR(初始保證金率)設定為 50% 時,MMR 可能高達 48%。在這種情況下,嘗試開設大頭寸的用戶被限制只能使用低槓桿,但 MMR 卻增加到不合理的程度。
這種設置限制了用戶有效利用其資金的能力,因槓桿級別的突變要求頻繁調整,降低了靈活性。這樣就造成了風險管理和用戶體驗之間的不平衡,使得大額投資者難以在這些限制下高效運作。
2.2 MMR 和 IMR
MMR(維持保證金率)主要用於幫助交易所管理清算風險,作為一種補償機制。從本質上講,MMR 反映了流動性提取的壓力,並需要隨著未平倉頭寸的變化而動態調整。以下是基於交易所可獲取的流動性相關指標推導出的 MMR 理論值。
2.2.1 流動性相關變量
為了準確評估流動性,確定了以下變量,這些變量通常對交易所可見:
•μ:市場訂單執行速度
•T:清算或交易所需的時間
•i :與最佳買價或賣價的距離(價位層次)
•j :報價時間單位
•Qi:距訂單簿距離為 的訂單平均數量
•S:訂單的平均規模(市場訂單用 ,限價訂單用 表示)
•N:訂單的數量(市場訂單用 ,撤單用 ,限價訂單用 表示)
這些數值代表了穩定市場中的平均情況。
2.2.2 用戶頭寸指標定義
• position:所有用戶的瞬時平均頭寸規模,可以從交易所的歷史數據中獲得。
• pos:任何單一用戶持有的頭寸規模。
• X:在 MMR 範圍內的交易期間成交量之和。
• MMRup:MMR 的上限。
• rMMR:MMR 的最終值。
• R:與最佳買價或賣價的實際距離,不同於 r ,通常依賴於 i 、 j 。
2.2.3 隨訂單流調整 MMR
限價單的進入和撤銷速度被納入多個層次的平均值中。由於市場訂單更可能立即執行,需要考慮相對的增加或減少。以下關係式定義了此動態變化:
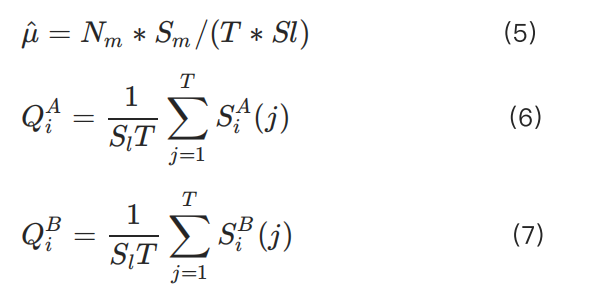
例如,對於多頭頭寸,強勁的清算流動性可以是買單數量(Q):
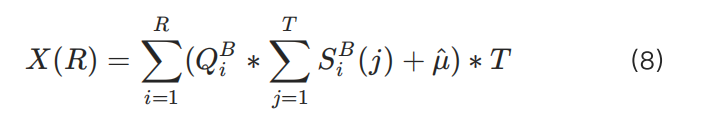
為保證交易所的安全性,得出以下公式:

在這裡可以看到,頭寸與 R之間呈近似反比關係。對於最小訂單數量:

已知頭寸時,變量的約束關係使得 MMR 獨立於 p,因此:
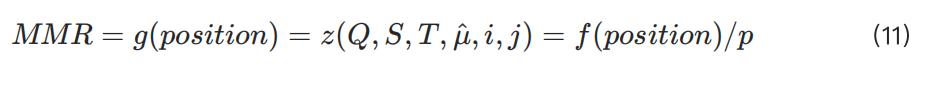
最終的 rMMR 值可以表達為:
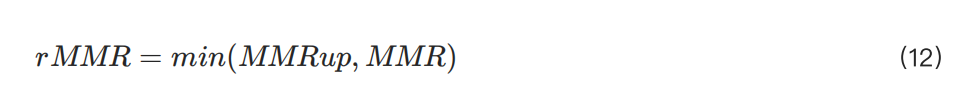
從上述方程可以看出,除 R 外,其他變量如頭寸、 Q、 S 和 T 均已確定。因此, 可從這些變量中推導出來,進而計算 MMR 和 rMMR。
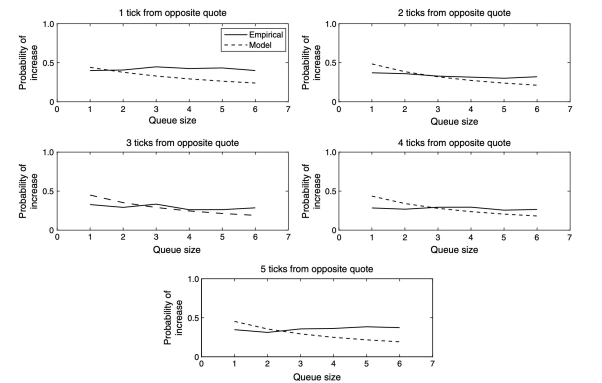
此外,需要設置 MMRup 上限,因為模型往往傾向於保守估計,忽略了關鍵價位和買賣盤重要層級對訂單簿的正面影響。一些來自 CME 的研究(見圖 2)更準確地展示了這種影響。
IMR(初始保證金率)通常與基礎資產的槓桿和流動性相關,因此通常需要根據頭寸規模等因素進行動態調整。可以定義為:
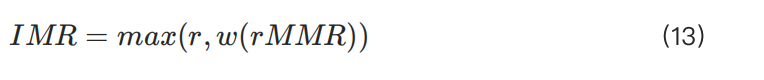
在這裡,IMR 對應於第 2.1 節中提到的初始保證金率 r。函數 w(rMMR) 提供了更大的靈活性。例如,如果交易所認為其流動性較為穩定,可以採用簡單的調整方式,如:w(rMMR)=1.3×rMMR。
這種方法為動態調整保證金率提供了切實可行的途徑,確保 IMR 反映當前的市場狀況和流動性水平。與固定的保證金規則相比,這使系統更具適應性,通過有效的風險管理惠及用戶和交易所雙方。
3 近似解 k
參數k是為每個特定資產(交易對)設定的全局參數,不需要考慮現有訂單或未平倉頭寸。原則上,k的值越大,用戶能夠開設的頭寸越多。然而,這裡存在一個關鍵限制:允許的最大頭寸所需的保證金不能超過總資本乘以 IMR 的值。
為簡化,我們將允許的最大頭寸公式賦值為變量 :
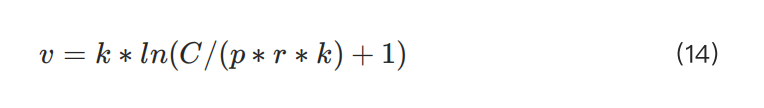
實際槓桿必須小於或等於已使用保證金的倒數:
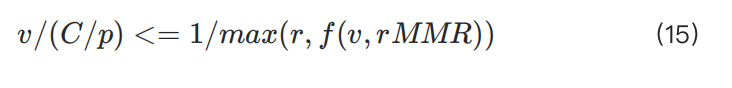
引入新變量 y 以代替 C(資本)和 p(價格)來簡化計算:

得到:
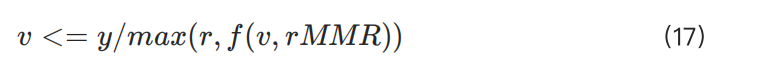
除了極小的頭寸外,簡化的調整 1.3 × rMMR (使用 f(pos,rMMR)通常小於 r。對於較小的頭寸,所需的保證金變得可忽略,因此此類情境不在我們的風險模型考慮範圍內。同樣,由於 MMRup 設定了上限,在此上下文中也可忽略。
因此,我們只需考慮 1/IMR的最小可能值。該不等式因此可簡化為:
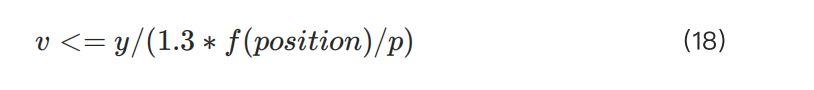
該不等式展示了最大允許頭寸與實際槓桿之間的關係。
與其他變量不同,頭寸和 R 具有明確的反比關係。因此,從 R 推導的 MMR 也可以和頭寸成反比例關係,並表示為:

假設在低頭寸條件下,MMR 符合傳統形式(槓桿的倒數的一半),公式可以寫為:
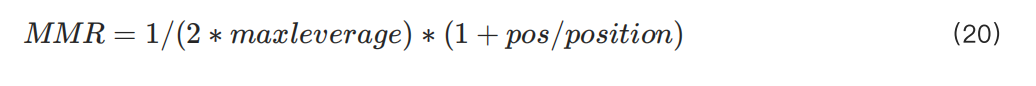
此時,若嘗試尋找k的極限值,則公式 (3) 中的 r 將變為 1/maxleverage。
替換變量後,不等式 (18) 可變為:
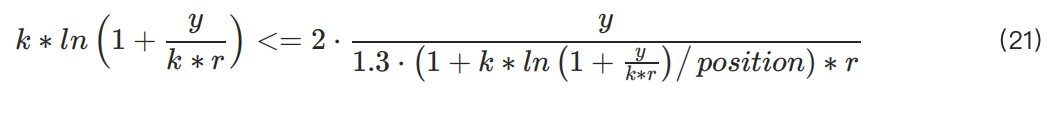
我們觀察到y(由用戶資本決定)理論上不應影響k的值。因此,k 主要依賴於頭寸。儘管k的最小值會隨 y 變化,但目標是找出在所有條件下的最小可能值,從而確保在任何場景下開倉的安全性。
此處 y/(k*r) 仍可替換為一個變量,但方程依然複雜,難以通過解析解求出。經過大量近似實驗和迭代模擬發現,k 會收斂於一個非常簡單的表達式(但k的計算相當複雜,此處不做詳細說明):
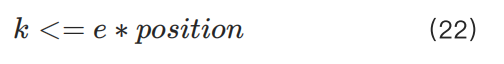
通過調整 k 或頭寸的值,可以達到在資金量或未平倉頭寸數量不大的情況下,用戶可以開設到 C/(p∗r)的頭寸。否則,將受到限制。數量的規模和限制程度由k和頭寸共同控制。因此,不同的加密貨幣往往對應不同的k值。
4 結論
以上是 KuCoin 全倉風險限額系統的簡要介紹。該設計的優勢及其對用戶的友好性顯而易見。在 KuCoin 的全倉系統中,除了風險限額,其他元素如風險比率和訂單保證金的使用也通過標記價格進行動態管理。這種動態管理不僅最大化釋放了用戶的保證金,也與新的風險限額框架無縫集成,從而提升了系統效率和用戶體驗。
5 附錄
圖 1:
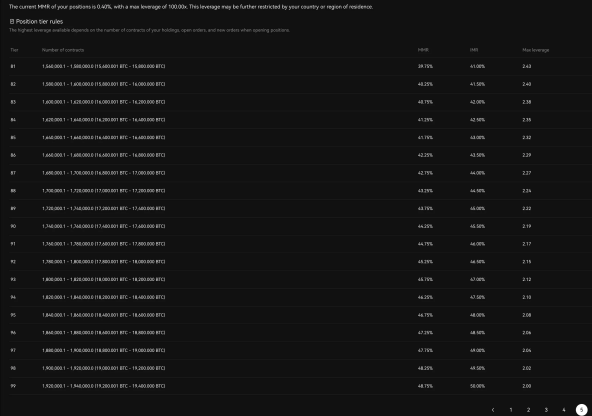
圖 2:
6 參考文獻
1. Rama Cont, Sasha Stoikov 和 Rishi Talreja,《A Stochastic Model for Order Book Dynamics》,《Operations Research》,2010 年,第 58 卷,第 3 期,第 549–563 頁。
2. 《Forecasting Initial Margin Requirements — A Model Evaluation》,《Journal of Financial Markets》,第 40 卷,2018 年。
3. Alfonsi, A., A. Schied, A. Schulz,《Optimal execution strategies in limit order books with general shape functions》,《Quant. Finance》,2010 年,第 10 卷,第 2 期,第 143–157 頁。







