以太坊協議可能的未來（六）：The Splurge

計劃深入優化以太坊協議，旨在提升網絡效率與可持續性。它不僅可能突破技術瓶頸，更有望革新區塊鏈安全與隱私。

原文：Possible futures of the Ethereum protocol, part 6: The Splurge（vitalik.eth）

作者：vitalik.eth

編譯：Yewlne，LXDAO

封面：Galaxy

譯者前言

在區塊鏈技術飛速發展的今天，系統架構的複雜度也在逐漸提升，給開發者和用戶都帶來了新的挑戰。“The Splurge” 計劃強調通過優化和完善現有協議細節，來提升網絡的效率和可持續性。這些前沿技術的探索，不僅有望解決當前的技術瓶頸，還可能徹底改變區塊鏈的安全和隱私機制，使之更接近於 “無信任” 的理想狀態。希望這次翻譯能夠幫助更多的中文讀者瞭解以太坊協議的最新進展，激發大家對這些重要但常被忽視的主題的興趣。

本文概述

本文共約 10,000 字，有 5 個部分，閱讀完本文預計需要 55 分鐘。

• EVM 改進
• 賬戶抽象
• EIP-1559 改進
• 可驗證延遲函數（VDFs）
• 混淆和一次性簽名：密碼學的未來

正文內容

《以太坊協議可能的未來（六）：The Splurge》

特別鳴謝 Justin Drake 和 Tim Beiko 的反饋與評審。

有些東西很難歸入單一類別。以太坊協議設計中存在許多 “小細節”，它們對以太坊的成功至關重要，但難以妥善歸類到更大的子類別中。在實踐中，其中約一半內容涉及各種形式的 EVM 改進，其餘則包含各種細分主題。這就是 "Splurge" 升級的目標所在。

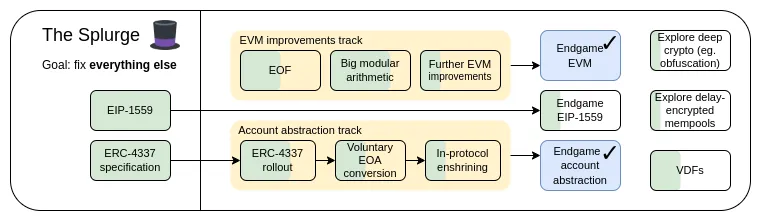
The Splurge：關鍵目標

• 將 EVM 引導至高性能且穩定的 “終局狀態”。
• 將賬戶抽象引入協議層，讓所有用戶都能受益於更安全、更便捷的賬戶。
• 優化交易費用經濟模型，在提升可擴展性的同時降低風險。
• 探索先進的密碼學技術，從長遠來看可以使以太坊變得更好。

本章內容：

• EVM 改進
• 賬戶抽象
• EIP-1559 改進
• 可驗證延遲函數（VDFs）
• 混淆和一次性簽名：密碼學的未來

EVM 改進

它解決什麼問題？

目前的 EVM 難以進行靜態分析，這使得實現高效部署、進行代碼形式化驗證以及後續擴展變得困難。另外，由於其效率很低，除非通過預編譯明確支持，否則很難實現多種高級密碼學運算。

它是什麼，它是如何工作的？

當前的 EVM 改進路線圖中，首要步驟就是計劃在下次硬分叉中引入的 EVM 對象格式（EOF）。EOF 包含了一系列 EIP 提案，這些提案為 EVM 定義了一個新版本的代碼格式，具有以下幾個關鍵特性：

• 實現了代碼（可執行但無法從 EVM 中讀取）與數據（可讀取但不可執行）的分離
• 禁用動態跳轉機制，僅保留靜態跳轉
• EVM 代碼將無法獲取 gas 相關信息
• 新增了顯式的子程序調用機制

老版本的合約將可以繼續使用且允許創建，不過未來可能會逐步淘汰舊版合約 (甚至可能強制將它們轉換為 EOF 格式)。新版本的合約則可以享受 EOF 帶來的效率提升：一方面可以通過子程序特性略微減小字節碼體積，另一方面也能從 EOF 獨有的新特性和更低的 gas 消耗中獲益。

EOF 引入後，使得後續升級變得更加容易。目前發展最成熟的是 EVM 模塊化算術擴展 (EVM-MAX)。EVM-MAX 專門為模運算設計了一組新的運算操作，並將它們放在一個新的內存空間中，其他指令無法訪問該空間。這使得系統可以採用一些優化算法，比如蒙哥馬利乘法。

一個較新的構思是將 EVM-MAX 與單指令多數據（SIMD）特性結合起來。SIMD 這個想法在以太坊社區已經存在很長時間了，最早可以追溯到 Greg Colvin 提出的 EIP-616。SIMD 可用於加快各類密碼學計算，包括哈希函數、基於 32 位的各種 STARK 證明（32-bit STARKs）和格密碼學（lattice-based cryptography）。EVM-MAX 結合 SIMD 這兩項擴展能很好地滿足 EVM 在性能方面的提升需求。

這個組合 EIP 的初步設計將以 EIP-6690 為基礎，並作如下擴展：

• 支持以下類型的模數：（i）任意奇數，或（ii）2 的 768 次方及以下的 2 的冪。
• 為每個 EVMMAX 指令（add、sub、mul）增加新版本。這個版本不是接收 3 個即時變量 x、y、z，而是接收 7 個即時變量：x_start、x_skip、y_start、y_skip、z_start、z_skip、count。

用 Python 代碼表示，這些指令的功能等同於：

for i in range(count):
    mem[z_start + z_skip * count] = op(        mem[x_start + x_skip * count],        mem[y_start + y_skip * count]    )

除非在實際實施中，它將被並行處理。

• 針對模數為 2 的冪的情況，將計劃添加 XOR、AND、OR、NOT 和 SHIFT（支持循環和非循環）等運算指令。此外還會添加 ISZERO 指令，用於將運算結果推送到 EVM 主棧。

這些功能足以支持實現橢圓曲線密碼學、小域密碼學（如 Poseidon、circle STARKs）、傳統哈希函數（如 SHA256、KECCAK、BLAKE）以及格密碼學（Lattice-based cryptography）。

其他 EVM 升級方案也有可能，但目前關注度還不高。

與現在研究有什麼聯繫？

• EOF: https://evmobjectformat.org/
• EVM-MAX: https://eips.ethereum.org/EIPS/eip-6690
• SIMD: https://eips.ethereum.org/EIPS/eip-616

還有什麼要做，以及需要權衡什麼？

目前計劃在下一次硬分叉中引入 EOF。儘管移除該功能仍有可能——此前也發生過在硬分叉前最後一刻移除特性的情況——但這將面臨諸多阻力。如果移除 EOF，意味著後續所有 EVM 升級都需要在不具備 EOF 的情況下進行，這雖然可行但會帶來更多技術挑戰。

EVM 的主要取捨在於 L1 複雜度與基礎架構複雜度之間的平衡。EOF 將會給 EVM 實現增加顯著數量的代碼，且靜態代碼檢查也非常複雜。作為回報，我們能獲得高級語言的簡化、EVM 實現的簡化以及其他收益。可以說，任何優先考慮以太坊 L1 持續改進的路線圖都應該包含 EOF 並以此為基礎。

其中一項重要的工作是實現類似於 EVM-MAX 結合 SIMD 這樣的功能，並對各種密碼學操作進行 gas 消耗的基準測試。

它與路線圖的其他部分如何互動？

L1 對 EVM 的調整能夠促進 L2 作出相應改變。如果其中一層單獨調整而另一層不變，就會引發一些兼容性問題，這會帶來其他負面影響。此外，EVM-MAX 結合 SIMD 功能可以降低多種證明系統的 gas 成本，從而提升 L2 層的執行效率。這也便於移除更多預編譯模塊，因為可以用 EVM 代碼替代這些模塊，且基本不會對效率造成大的影響。

賬戶抽象

解決了什麼問題？

目前，交易僅支持一種驗證方式：ECDSA 簽名。最初，賬戶抽象旨在突破這一限制，使賬戶驗證邏輯可以使用任意 EVM 代碼實現。這將能夠支持多種應用場景：

• 遷移至抗量子密碼學
• 輪換舊密鑰（這是普遍認可的安全實踐）
• 多籤錢包和社交恢復錢包。
• 對低價值操作使用單一密鑰，對高價值操作使用其他密鑰（或密鑰組）
• 實現無中繼器的隱私協議，顯著降低系統複雜度並消除核心依賴點

自 2015 年賬戶抽象概念提出以來，其目標範圍已經擴大，增加了許多 “便利性目標”，例如允許一個沒有 ETH 但持有特定 ERC20 代幣的賬戶直接使用該 ERC20 代幣支付 gas 費用。下圖總結了這些目標：

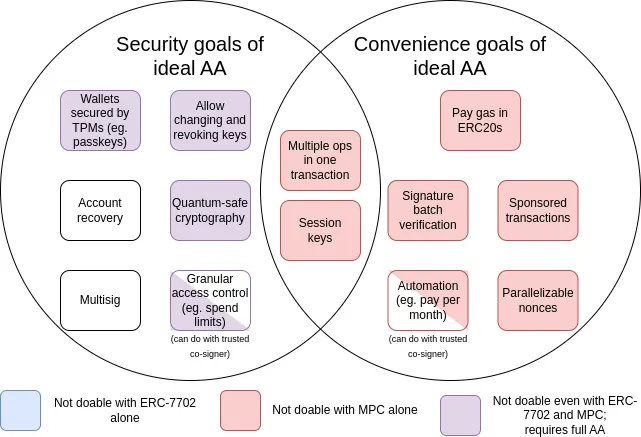
這裡的 MPC 指的是多方計算（multi-party computation）：這是一種已有 40 年曆史的技術，它將密鑰分片存儲到多個設備中，並通過密碼學方法在不直接合並密鑰分片的情況下生成簽名。

EIP-7702 是計劃在下一次硬分叉中引入的提案。EIP-7702 的出現源於人們越來越認識到，有必要為所有用戶（包括 EOA 用戶）提供賬戶抽象的便利功能，以在短期內改善所有人的用戶體驗，並避免生態系統分裂為兩個獨立的系統。這項工作始於 EIP-3074，最終形成了 EIP-7702。EIP-7702 使賬戶抽象的 “便利功能” 立即可供所有用戶使用，包括 EOA（外部擁有賬戶，即由 ECDSA 簽名控制的賬戶）。

從圖表中可以看出，雖然某些挑戰（特別是 “便利性” 方面的挑戰可以通過多方計算協議或 EIP-7702 等漸進式技術來解決，但推動最初賬戶抽象提案的大部分安全目標，只能通過迴歸並解決最初的問題來實現：即允許智能合約代碼直接控制交易驗證過程。然而，至今尚未實現這一點的原因是，要安全地實現這一功能本身就是一項挑戰。

這是什麼，它是如何工作的?

從本質上說，賬戶抽象的核心很簡單：允許智能合約，而不僅僅是外部擁有賬戶（EOA），來發起交易。所有的複雜性都源於如何以一種既有助於維護去中心化網絡，又能防範拒絕服務（DoS）攻擊的方式來實現這一點。

一個能夠闡明這一關鍵挑戰的典型例子是多重無效化問題（Multi-invalidation Problem）：

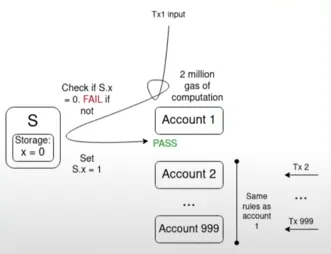
如果有 1000 個賬戶的驗證函數都依賴於某個共享的值 S，並且在當前 S 值下，內存池中存在許多有效的交易，那麼一筆改變 S 值的交易可能會使內存池中的所有其他交易失效。這使得攻擊者可以以極低的成本向內存池發送垃圾交易，佔用網絡節點的資源。

多年來，為了在擴展功能的同時限制拒絕服務（DoS）攻擊的風險，人們付出了大量的努力，最終，有一種解決方案使大家就如何實現 “理想的賬戶抽象” 達成了共識：ERC-4337。

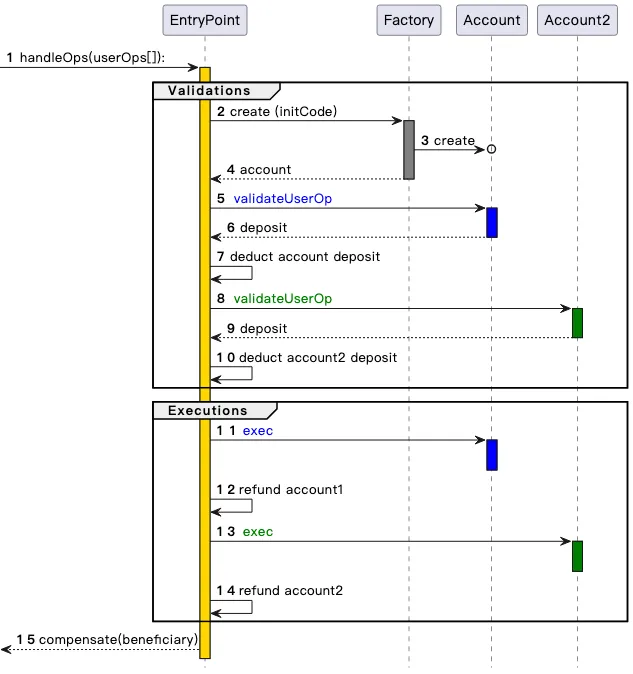
ERC-4337 的工作原理是將用戶操作的處理分為兩個階段：驗證和執行。首先處理所有的驗證，然後再處理所有的執行。在內存池中，只有當用戶操作的驗證階段僅涉及其自身賬戶，且不讀取環境變量時，該操作才會被接受。這可以防止多重無效化攻擊。同時，對驗證步驟也設定了嚴格的 gas 限制。

ERC-4337 最初被設計為一個協議外的標準（ERC），這是因為當時以太坊客戶端開發人員正專注於升級 “The Merge” 工作，沒有多餘的精力開發其他功能。這就是為什麼 ERC-4337 使用了名為用戶操作（User Operations）的自定義對象，而不是常規交易。然而，最近我們意識到，有必要將其部分內容納入協議中。主要有兩個原因：

• EntryPoint 作為合約所固有的效率低下問題：每個捆綁操作需要額外約 10 萬 gas，每個用戶操作還需要額外數千 gas。
• 需要確保以太坊的特性，例如由包含列表（inclusion lists）提供的包含保證，能夠適用於賬戶抽象用戶。

此外，ERC-4337 還擴展了兩個功能：

• 支付主體（Paymasters）：該功能允許一個賬戶代表另一個賬戶支付費用。這違反了驗證階段只能訪問發送賬戶自身的規則，因此引入了特殊處理機制來支持支付主體機制並確保其安全性。
• 聚合器（Aggregators）：該功能支持簽名聚合，例如 BLS 聚合或基於 SNARK 的聚合。這對於在 Rollups 上實現最高水平的數據效率是必不可少的。

有哪些現有的研究資料？

• 賬戶抽象歷史演進的演講：https://www.youtube.com/watch?v=iLf8qpOmxQc
• ERC-4337：https://eips.ethereum.org/EIPS/eip-4337
• EIP-7702：https://eips.ethereum.org/EIPS/eip-7702
• BLSWallet 代碼（聚合功能）：https://github.com/getwax/bls-wallet
• EIP-7562（寫入協議的賬戶抽象）：https://eips.ethereum.org/EIPS/eip-7562
• EIP-7701（基於 EOF 的寫入協議賬戶抽象）：https://eips.ethereum.org/EIPS/eip-7701

還有什麼需要做，以及有哪些權衡？

剩餘的主要問題是確定如何將賬戶抽象化完全納入協議中。最近一個備受關注的賬戶抽象寫入協議的提案是 EIP-7701，它在 EOF 的基礎上實現了賬戶抽象。賬戶可以擁有一個獨立的驗證代碼段，如果賬戶設置了對應代碼段，那麼在該賬戶發起的交易的驗證步驟中就會執行該代碼。

有趣的是，這種方法清晰地展現了兩種等價的原生賬戶抽象實現方式：

1. 將 EIP-4337 納入協議中
2. 一種新型的 EOA，其簽名算法由 EVM 代碼執行

如果我們一開始就對驗證過程中可執行代碼的複雜性設置嚴格限制——不允許訪問外部狀態，甚至最初設置的 gas 限制低到無法用於抗量子或隱私保護應用——那麼這種方法的安全性就非常明確：它只是用耗時相近的 EVM 代碼執行替代 ECDSA 驗證。然而，隨著時間的推移，我們需要放寬這些限制，因為允許隱私保護應用無需中繼器即可運行，以及實現抗量子能力，都非常重要。為此，我們確實需要找到更靈活的方式來應對拒絕服務（DoS）風險，而不是要求驗證步驟極度簡化。

主要的權衡似乎在於：是更早地將一個較少人滿意的方案寫入協議，還是等待更長時間，可能獲得一個更理想的解決方案。理想的方法可能是某種混合方案。一種混合方案是更快地將某些用例納入協議，留出更多時間來解決其他問題。另一種方法是先在 L2 上率先部署更激進的賬戶抽象版本。然而，這面臨的挑戰是，要讓 L2 團隊願意採納一個提案，他們需要確信 L1 和其他 L2 日後會採用兼容的方案。

另一個我們需要明確考慮的應用是密鑰庫賬戶，它在 L1 或專用的 L2 上存儲賬戶相關狀態，但可以在 L1 和任何兼容的 L2 上使用。要有效地實現這一點，可能需要 L2 支持 L1SLOAD 或 REMOTESTATICCALL 等指令，不過這也要求 L2 上的賬戶抽象實現能夠支持它。

它如何與路線圖的其他部分互動？

包含列表（Inclusion Lists）需要支持賬戶抽象交易。實際上，包含列表和去中心化內存池的需求最終非常相似，儘管包含列表有更多的靈活性。此外，理想情況下，L1 和 L2 上的賬戶抽象實現應儘可能保持一致。如果我們預計未來大多數用戶將使用 keystore Rollups，賬戶抽象設計就應該考慮到這一點。

EIP-1559 改進

它解決了什麼問題？

EIP-1559 於 2021 年在以太坊上實施，顯著改善了平均區塊包含時間。

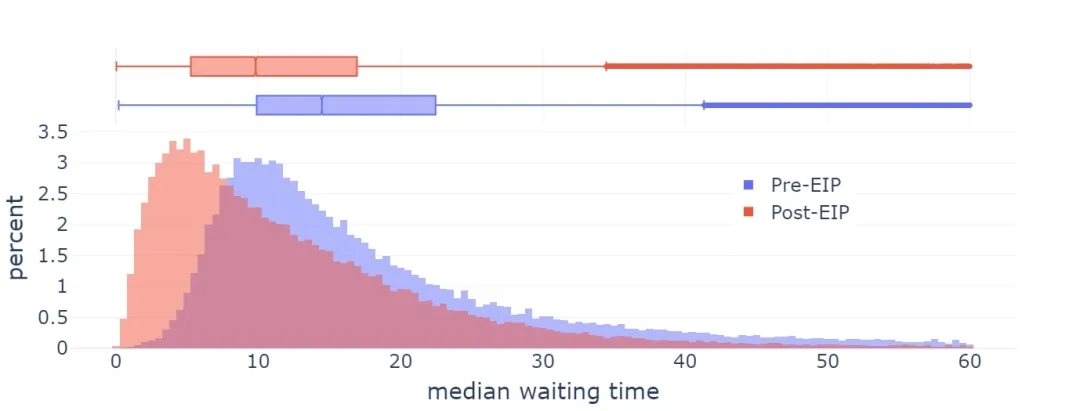
然而，目前 EIP-1559 的實現存在幾個不完善之處：

• 公式略有缺陷：它的目標是填滿約 50-53% 的區塊（取決於方差），而不是 50%（這與數學家所說的 “算術-幾何均值不等式” 有關）
• 在極端情況下，調整速度不夠快。

後來用於數據塊（blobs）的公式（EIP-4844）在設計時就明確考慮瞭解決第一個問題，整體上也更加簡潔。無論是 EIP-1559 本身還是 EIP-4844，都沒有嘗試解決第二個問題。因此，當前的狀況是一個令人困惑的過渡狀態，涉及兩種不同的機制，甚至有理由認為，隨著時間的推移，這兩種機制都需要改進。

此外，以太坊的資源定價還存在其他一些區別於 EIP-1559 的弱點，但可以通過調整 EIP-1559 來解決這些問題。其中一個主要問題是平均情況與最壞情況之間的差異：以太坊的資源價格必須設定為能夠處理最壞情況（即一個區塊的所有 gas 消耗會佔用一個資源），但平均使用量遠低於此，這導致了效率低下。

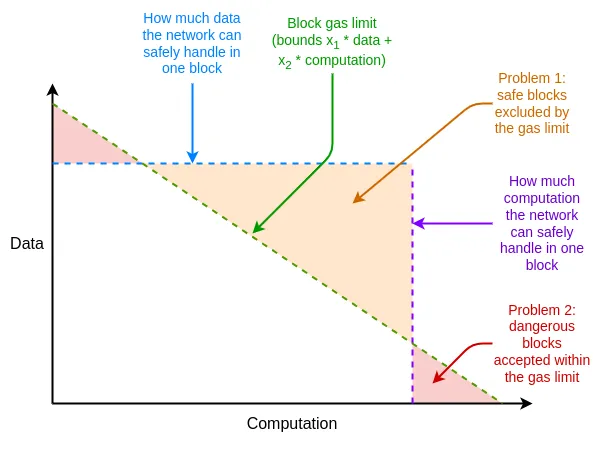
它是什麼，它是如何工作的?

解決這些效率低下問題的方案是多維 Gas：為不同的資源設置獨立的價格和限制。從技術上講，這一概念獨立於 EIP-1559，但 EIP-1559 使其更易於實現：在沒有 EIP-1559 的情況下，面對多種資源約束，最優地打包區塊是一個複雜的多維揹包問題（multidimensional knapsack problem）。而有了 EIP-1559，大多數區塊在任何資源上都未達到滿負荷，因此簡單的 “接受任何支付足夠費用的交易” 算法即可滿足需求。

我們現在已經有了執行和數據塊（blobs）的多維 gas；原則上，我們可以增加更多維度：調用數據（calldata）、狀態讀寫和狀態大小擴展。

EIP-7706 為 calldata 引入了一個新的 gas 維度。同時，它通過使三種類型的 gas 都遵循一個（EIP-4844 風格的）框架來簡化多維 gas 機制，從而也解決了 EIP-1559 的數學缺陷。

EIP-7623 是一個更為精細的解決方案，用於應對平均情況與最壞情況的資源問題。它在不引入全新維度的情況下，更嚴格地限定了最大調用數據（calldata）。

更進一步的方向是解決更新速率問題，找到一個更快速的基礎費用（base fee）算法，同時保持 EIP-4844 機制引入的關鍵不變量（即：從長遠來看，平均使用量會更精確地接近目標值）。

有哪些現有的研究資料？

• EIP-1559 常見問題解答：https://notes.ethereum.org/@vbuterin/eip-1559-faq
• EIP-1559 實證分析：https://dl.acm.org/doi/10.1145/3548606.3559341
• 關於快速調整的改進提案：https://kclpure.kcl.ac.uk/ws/portalfiles/portal/180741021/Transaction_Fees_on_a_Honeymoon_Ethereums_EIP_1559_One_Month_Later.pdf
• EIP-4844 常見問題解答，基礎費用機制部分：https://notes.ethereum.org/@vbuterin/proto_danksharding_faq#How-does-the-exponential-EIP-1559-blob-fee-adjustment-mechanism-work
• EIP-7706：https://eips.ethereum.org/EIPS/eip-7706
• EIP-7623：https://eips.ethereum.org/EIPS/eip-7623
• 多維 Gas：https://vitalik.eth.limo/general/2024/05/09/multidim.html

還有什麼需要做，以及有哪些權衡？

多維 Gas 有兩個主要的權衡：

• 增加了協議的複雜性
• 增加了填充區塊容量所需的最優算法的複雜性

對於調用數據（calldata），協議複雜性是一個相對較小的問題，但對於位於 EVM 內部的 gas 維度（如存儲讀寫）而言，這個問題就更為嚴重。問題在於，設置 gas 限制的不僅僅是用戶：當合約調用其他合約時，它們也會設置限制。而目前，它們設置限制的方式仍是單一維度的。

消除這個問題的一個簡單方法是僅在 EOF 內部提供多維 gas，因為 EOF 不允許合約在調用其他合約時設置 gas 限制。非 EOF 合約在進行存儲操作時，必須為所有類型的 gas 支付費用（例如，如果一次 SLOAD 操作消耗了區塊存儲訪問 gas 限制的 0.03%，那麼非 EOF 用戶也會被收取執行 gas 限制的 0.03%）。

對多維 Gas 進行更多的研究，將非常有助於理解這些權衡並找到理想的平衡點。

它如何與路線圖的其他部分互動？

多維 Gas 的成功實現可以大幅減少某些 “最壞情況” 的資源使用，從而減輕為了支持例如基於 STARK 的哈希樹而進行性能優化的壓力。對狀態大小增長設定明確的目標，可以使客戶端開發者更容易規劃和估計他們未來的需求。

如上所述，由於 EOF 具有 gas 不可觀測性特徵，它使得更高級版本的多維 Gas 更容易實現。

可驗證延遲函數（VDFs）

它解決了什麼問題？

目前，以太坊使用基於 RANDAO 的隨機數來選擇提議者。RANDAO 隨機數的工作原理是要求每個提議者揭示他們預先承諾的秘密，並將揭示的每個秘密混合到隨機數中。因此，每個提議者都有 “1 比特的操縱能力”：他們可以通過不出塊（需要付出代價）來改變隨機數。這對於選擇提議者來說尚可接受，因為放棄一次機會以獲得兩次新的提議機會的情況非常罕見。但對於需要隨機數的鏈上應用程序來說，這是不可接受的。理想情況下，我們需要找到一個更穩健的隨機數來源。

它是什麼, 它是如何工作的?

可驗證延遲函數（VDF）是一種只能順序計算、無法通過並行化加速的函數。一個簡單的例子是重複哈希計算：執行 for i in range(10**9): x = hash(x)。輸出結果，連同證明其正確性的 SNARK 證明，可以用作隨機值。其思想是，輸入基於在時間 T 可獲得的信息選擇，而輸出在時間 T 時尚未知曉：只有當某人完全運行完計算後的一段時間後才可用。由於任何人都可以運行此計算，無法扣留結果，因此也就無法操縱結果。

可驗證延遲函數的主要風險是意外優化：有人找到了一種比預期快得多的運行該函數的方法，使他們能夠根據未來的輸出，操縱他們在時間 T 時所揭示的信息。意外優化可能以兩種方式發生：

• 硬件加速：有人制造了一種 ASIC，可以比現有硬件更快地運行計算循環。
• 意外並行化：有人找到了一種通過並行化更快運行該函數的方法，即使這樣做需要消耗超過 100 倍的資源。

創建一個成功的 VDF 的任務在於避免上述兩個問題，同時確效率足夠實用（例如，基於哈希的方法存在一個問題，即實時對哈希進行 SNARK 證明需要極高的硬件要求）。硬件加速問題通常通過讓公共物品參與者自行創建並分發接近最優的 VDF 專用 ASIC 來解決。

有哪些現有的研究資料？

• VDF 研究網站：https://vdfresearch.org/
• 關於針對以太坊中使用的 VDFs 攻擊的思考，2018 年：https://ethresear.ch/t/verifiable-delay-functions-and-attacks/2365
• 針對 MinRoot（一個提議的 VDF）的攻擊研究：https://inria.hal.science/hal-04320126/file/minrootanalysis2023.pdf

還有什麼需要做，以及有哪些權衡？

目前，還沒有一個在各方面都能完全滿足以太坊研究人員要求的 VDF 構造。找到這樣一個函數還需要更多的工作。如果我們有了這樣的函數，主要的權衡就是是否將其納入協議：這只是一個在功能性與協議複雜性和安全風險之間的簡單取捨。如果我們認為一個 VDF 是安全的，但最終被證明是不安全的，那麼根據其實現方式，安全性會降級到 RANDAO 假設（每個攻擊者有 1 比特的操縱能力）或略差的程度。因此，即使 VDF 存在缺陷，也不會破壞協議本身，儘管它會破壞那些嚴重依賴它的應用程序或任何新的協議特性。

它如何與路線圖的其他部分互動？

VDF 是以太坊協議中一個相對獨立的組成部分，除了提高提議者選擇的安全性外，它還可用於：（i）依賴隨機數的鏈上應用程序，以及潛在的（ii）加密內存池。然而，基於 VDF 的加密內存池的實現仍然依賴於尚未實現的其他密碼學突破。

需要注意的是，考慮到硬件的不確定性，VDF 輸出的產生時間與其被需要的時間之間可能會有一些 “延遲”。這意味著信息可能會在提前幾個區塊時就被獲取。這可能是一個可以接受的代價，但在設計諸如最終確定性或委員會選擇機制時，應將其考慮在內。

混淆和一次性簽名：密碼學的未來

它解決了什麼問題？

Nick Szabo 最著名的文章之一是 1997 年發表的一篇關於 “上帝協議” 的文章。在這篇文章中，他指出多方應用程序經常依賴於 “可信第三方” 來管理交互。在他看來，密碼學的作用是創建一個模擬的可信第三方來完成相同的工作，而無需實際信任任何特定參與者。

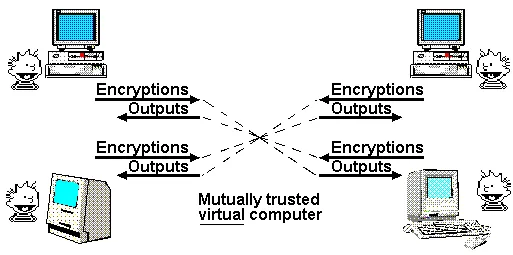
到目前為止，我們只能部分地接近這個理想。如果我們只需要一個透明的虛擬計算機，其中數據和計算無法被關閉、審查或篡改，而隱私不是目標，那麼區塊鏈可以實現這一點，儘管其可擴展性有限。如果隱私確實是目標，那麼直到最近，我們只能為特定應用創建一些專用協議：用於基本認證的數字簽名、用於原始形式的匿名性的環簽名和可鏈接環簽名、在特定可信發行者假設下實現更便捷加密的基於身份的加密、用於 Chaumian 電子現金的盲簽名等。這種方法需要為每個新應用投入大量工作。

在 2010 年代，我們首次看到了一種基於可編程密碼學的全新且更強大的方法。我們無需為每個新應用開發專用協議，而是可以使用新型強大的協議——特別是 ZK-SNARKs，為任意程序添加密碼學保證。ZK-SNARKs 讓用戶能夠證明他們所持有數據的任意陳述，且這種證明（i）易於驗證，（ii）除陳述本身外不會洩露任何數據。這在隱私性和可擴展性方面都取得了突破性進展，我將其比作人工智能領域中 Transformer 的影響力。數千年的人力投入到特定應用的工作中，突然被一個通用解決方案所替代，這個方案可以即插即用地解決大量意想不到的問題。

但 ZK-SNARKs 只是三大超級強大的通用型基礎協議之一。這些協議如此強大，以至於當我想到它們時，它們讓我想起了遊戲王（Yu-Gi-Oh）。遊戲王是我童年時期常玩的卡牌遊戲和觀看的動畫片：埃及神卡。埃及神卡是三張極其強大的卡牌，傳說它們的出現可能是致命的，而且它們太過強大以至於在決鬥中被禁止使用。類似地，在密碼學中，我們也有三個埃及神協議：

它是什麼，它是如何工作的?

ZK-SNARKs 是這三大協議中已經發展得相當成熟的一個。在過去五年裡，隨著證明生成速度和開發友好度的顯著提升，ZK-SNARKs 已成為以太坊在可擴展性和隱私性方面的基礎技術。但 ZK-SNARKs 存在一個關鍵限制：必須掌握數據才能對其生成證明。ZK-SNARK 應用中，每個狀態數據必須有唯一的 “所有者”，且任何讀寫操作都需要該所有者在場授權。

第二個協議克服了這一限制，它是全同態加密（Fully Homomorphic Encryption，FHE）。FHE 能夠在不訪問原始數據的情況下對加密數據執行任意計算。這使我們能夠在保護數據和算法隱私的前提下，為用戶處理其數據。它還能夠增強 MACI 等投票系統，提供近乎完美的安全性和隱私性保證。FHE 曾長期被認為效率過低而難以實用，但如今其效率已達到實用水平，相關應用也開始湧現。

但 FHE 也存在侷限：任何基於 FHE 的技術仍需要特定主體持有解密密鑰。雖然可以採用 M-of-N 多方分儲方案，甚至可以使用可信執行環境（TEE）作為第二重防護，但這仍是一個固有限制。

這引出了第三個協議，其威力超過前兩者的總和：不可區分混淆（Indistinguishability Obfuscation）。儘管它距離實用化還非常遙遠，但在 2020 年，我們已經基於標準安全假設建立了理論可行的協議，且近期已開始著手實現。不可區分混淆能夠讓你創建一個 “加密程序”，該程序可執行任意計算，同時完全隱藏其內部實現細節。舉個簡單例子，你可以將私鑰封裝進混淆程序中，使其僅能用於質數簽名，然後將程序分發給他人。使用者可以用該程序對任意質數進行簽名，但無法提取出私鑰。但這僅是其能力的冰山一角：結合哈希函數，它可以實現任何其他密碼學原語，並支持更多高級功能。

混淆程序唯一的限制在於無法防止程序本身被複制。不過，在這個領域已經出現了一項更強大的技術，只是它需要所有參與者都具備量子計算機：量子一次性簽名（Quantum One-Shot Signatures）。

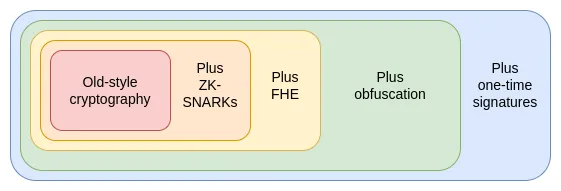
結合混淆技術和一次性簽名，我們幾乎可以構建完美的無信任第三方系統。唯一需要依賴區塊鏈而無法僅通過密碼學實現的，是抗審查能力。這些技術不僅能增強以太坊本身的安全性，還能支持構建更強大的上層應用。

為了解這些基礎協議如何各自提升系統能力，讓我們以一個典型案例來說明：投票系統。投票是一個極具挑戰性的問題，因為它需要滿足諸多複雜的安全屬性，特別是在可驗證性和隱私性方面都有極高要求。雖然強安全性的投票協議已存在數十年，但讓我們設定更高的目標：設計一個能支持任意投票協議的系統，包括二次投票、配對約束二次方融資、群集匹配二次方融資等。換言之，我們期望 “計票” 環節能夠支持任意程序邏輯。

• 首先，假設我們將投票數據記錄在區塊鏈上。這能實現公開驗證（任何人都可以驗證最終結果的正確性，包括計票規則和投票資格規則）和抗審查能力（無法阻止用戶參與投票），但缺乏隱私保護。
• 然後，我們引入 ZK-SNARKs  技術。這實現了隱私保護：每票均為匿名，同時確保只有授權用戶可以投票，且每個用戶僅能投票一次。
• 接著，我們引入 MACI 機制。投票內容經加密後傳輸至中心服務器的解密密鑰。中心服務器負責執行計票流程，包括過濾重複票項，併發布證明結果正確性的 ZK-SNARK。這不僅保持了前述保障（即使服務器作弊也不例外！），而且在服務器誠實的情況下，還提供了抗脅迫保護：用戶無法證明自己的投票選擇，即便他們主動想要證明。這是因為儘管用戶可以證明某次投票行為，但無法證明自己沒有投過過另一張票來抵消之前的投票。這有效防止了賄選和其他攻擊行為。
• 我們在全同態加密（FHE）環境中執行計票，並通過 N/2-of-N 門限解密方案進行解密。這將抗脅迫保護機制從單點信任提升為 N/2 門限信任。
• 我們將計票程序進行代碼混淆，並設計混淆程序使其只有在獲得授權時才能輸出結果，該授權可以是區塊鏈共識證明、工作量證明或兩者的組合。這使得抗脅迫保護機制達到近乎完美的程度：在區塊鏈共識模式下，需要 51% 的驗證節點串通才能破解；在工作量證明模式下，即便全網串通，通過運行不同用戶子集的計票來還原單個用戶的投票行為也會耗費巨大成本。我們還可以在最終統計結果中引入微小的隨機擾動，進一步提高單個用戶投票行為的隱匿性。
• 我們引入一次性簽名機制，這是一種基於量子計算的基礎協議，能確保簽名僅可用於對特定類型消息進行一次性簽署。這實現了完全的抗脅迫保護。

不可區分混淆還能支持其他強大的應用場景。例如：

• 支持任意內部加密狀態的 DAO、鏈上拍賣及其他應用。
• 完全通用的可信設置：開發者可以創建一個包含密鑰的混淆程序，該程序能執行任意程序並輸出結果，將 hash(key, program) 作為輸入參數。任何人獲得此程序後，都能將程序嵌入自身，將程序原有密鑰與自己的密鑰合併，從而擴展初始化範圍。這可用於為任意協議生成 1-of-N 的可信初始化。
• 僅需簽名驗證的 ZK-SNARKs。實現方式簡單：通過可信初始化創建一個混淆程序，該程序僅在驗證 ZK-SNARK 有效時才用密鑰進行簽名。。
• 加密交易內存池。它極大地簡化了交易加密過程：交易僅在未來特定鏈上事件發生時才解密。這甚至可以包括 VDF（可驗證延遲函數）的成功執行。

通過一次性簽名機制，我們可以使區塊鏈免受破壞最終性的 51% 攻擊，但仍可能面臨審查攻擊。類似一次性簽名的基礎協議能夠支持量子貨幣，無需依賴區塊鏈就能解決雙花問題，但更復雜的應用場景仍需要區塊鏈支持。如果這些基礎協議能達到足夠的性能水平，世界上大多數應用都將具備去中心化的潛力。主要瓶頸在於如何驗證實現的正確性。

有哪些現有的研究資料？

• 2021 年不可區分混淆協議研究：https://eprint.iacr.org/2021/1334.pdf
• 混淆技術如何增益以太坊：https://ethresear.ch/t/how-obfuscation-can-help-ethereum/7380
• 首個一次性簽名構造方案：https://eprint.iacr.org/2020/107.pdf
• 混淆技術實現探索（1）：https://mediatum.ub.tum.de/doc/1246288/1246288.pdf
• 混淆技術實現探索（2）：https://github.com/SoraSuegami/iOMaker/tree/main

還有什麼需要做，以及有哪些權衡？

仍面臨諸多技術挑戰。 不可區分混淆技術目前仍非常不成熟，現有的構造方案運行速度慢了數百萬倍（甚至更多），無法在實際應用中使用。該技術因其運行時間 “理論上” 是多項式級別而廣為人知，但實際運行需要的時間比宇宙壽命還長。儘管近期的協議已降低了極端的時間開銷，但對於日常應用而言性能損耗仍然過高：據一位開發者估計，單次執行預計需要一年時間。

當前量子計算機尚未實現：目前網上所見的所有構想，要麼是僅能處理 4 位運算的原型系統，要麼不是真正意義的量子計算機——雖然它們可能包含量子組件，但無法執行實際有效的量子算法，如 Shor 算法或 Grover 算法。近期有跡象表明，“真正的” 量子計算機距離實現已不再那麼遙遠。然而，即便 “真正的” 量子計算機很快就會出現，普通人在筆記本電腦或手機上使用量子計算機的日子可能也比大型機構獲得能夠破解橢圓曲線密碼的量子計算機晚幾十年。

在不可區分混淆技術中，一個核心權衡點在於安全性假設。某些採用非常規假設的激進方案，雖然具有更實用的執行效率，但這些非常規假設往往存在被攻破的風險。隨著對格密碼學理論理解的深入，我們可能最終能夠建立不可破解的假設。但這種路徑風險較高。相對保守的路徑是堅持使用可證明歸約到 “標準假設” 的協議，但這意味著需要更長時間才能實現具備足夠執行效率的協議。

它如何與路線圖的其他部分互動？

強大的密碼學技術可能徹底改變遊戲規則。例如：

• 如果 ZK-SNARKs 的驗證像簽名一樣簡單，我們可能不再需要任何聚合協議，直接在鏈上完成驗證。
• 一次性簽名可能意味著更加安全的權益證明協議。
• 眾多複雜的隱私協議可能被一個 “僅僅” 支持隱私保護的 EVM 所替代。
• 加密交易內存池的實現變得更加容易。

起初，這些創新效益將體現在應用層，因為以太坊 L1 本質上需要在安全性假設上保持保守。不過，僅在應用層的採用也可能帶來革命性突破，堪比 ZK-SNARKs 的問世。

免責聲明：作為區塊鏈信息平臺，本站所發佈文章僅代表作者及嘉賓個人觀點，與 Web3Caff 立場無關。文章內的信息僅供參考，均不構成任何投資建議及要約，並請您遵守所在國家或地區的相關法律法規。