以太坊中更快的區塊/blob 傳播
感謝@n1shantd 、 @ppopth和 Ben Berger 對本文的討論和反饋,以及@dankrad的許多有益討論。
抽象的
我們建議通過使用隨機線性網絡編碼來改變我們在 P2P 網絡中廣播和傳輸塊和 blob 的方式。我們表明,理論上我們可以分發塊,佔用當前 gossipsub 實現所需時間的 5% 帶寬和 57% 的網絡跳數(因此每條消息的延遲為一半)。我們為計算開銷提供了具體的基準。
介紹
當前用於分發區塊的gossipsub機制大致如下。提議者從其所有對等體中挑選一個D=8對等體的隨機子集(稱為其網格),並將其區塊廣播給它們。每個接收區塊的對等體都會執行一些非常快速的初步驗證:主要是簽名驗證,但最重要的是不包括狀態轉換或交易執行。經過這種快速驗證後,對等體將其區塊重新廣播給另外D對等體。這種設計有兩個直接後果:
- 每次跳躍至少會增加以下延遲:從一個對等點到下一個對等點的一個完整塊傳輸(包括網絡 ping 延遲,本質上與帶寬無關,加上受帶寬限制的完整塊傳輸)。
- 對等方不必要地向已經收到完整塊的其他對等方廣播完整塊。
我們建議在廣播級別使用隨機線性網絡編碼(RLNC)。通過這種編碼,提議者會將區塊分成N塊(例如,對於以下所有模擬, N=10 ),而不是將完整區塊發送給約 8 個對等方,而是將單個塊發送給約 40 個對等方(不是原始塊之一,而是它們的隨機線性組合,請參閱下文的隱私考慮)。對等方仍然需要下載完整區塊,或者更確切地說是N塊,但它們可以從不同的對等方並行獲取它們。在收到這N塊(每個塊都是組成原始區塊的原始塊的隨機線性組合)後,對等方需要求解線性方程組來恢復完整區塊。
概念驗證實施突出了以下數字
- 提議一個區塊需要額外的 26 毫秒,該時間受 CPU 限制,在現代筆記本電腦(Apple M4 Pro)上可以完全並行化到不到 2 毫秒
- 驗證每個塊需要 2.6 毫秒。
- 解碼整個塊需要 1.4ms。
- 使用
10塊且D=40,每個節點發送的數據比當前的 gossipsub 要少一半,並且網絡可以在一半的時間內廣播 100KB 的塊,並且塊大小越大,收益就越大。
協議
有關網絡編碼的深入介紹,我們請讀者參閱 loc. cit. 和這本教科書。我們在此提到了上述概念驗證基準的最低限度的實現細節。在塊傳播(~110KB)的情況下,延遲或網絡跳數決定了傳播時間,而在完整 DAS 中的 blob 等大型消息的情況下,帶寬決定了傳播時間。
我們考慮一個具有素數特徵的有限域\mathbb{F}_p F p 。在上面的例子中,我們選擇了curve25519-dalek rust crate 實現的 Ristretto 標量基域。提議者採用一個塊(一個不透明的字節切片),並將其解釋為\mathbb{F}_p F p中元素的向量。在撰寫本文時,一個典型的以太坊塊約為B = 110KB B = 110 K B ,假設每個 Ristretto 標量需要少於 32 個字節來編碼,一個塊需要大約B/32 = 3520 B / 32 = 3520個\mathbb{F}_p F p元素。將其分成N=10塊,每個塊可視為\mathbb{F}_p^{M} F M p中的一個向量,其中M \sim 352 M ∼ 352 。因此,該塊可視為N N 個向量v_i \in \mathbb{F}^M_p v i ∈ F M p , i=1,...,N i = 1 , . . . , N 。提議者隨機選擇D\sim 40 D ∼ 40 個對等體的子集。對於每個這樣的對等體,它將發送一個\mathbb{F}_p^M F M p向量以及一些額外信息,以驗證消息並防止網絡上的 DOS。我們解釋提議者
提議者
我們將使用 Pedersen 承諾來實現上述 rust crate 實現的 Ristretto 橢圓曲線E E 。我們假設我們已經隨機選擇了足夠多元素的可信設置G_j \in E G j ∈ E , j = 1, ..., K j = 1 , . . . , K ,其中K \gg M K ≫ M 。我們為 \mathbb { F } _p ^ M F M p選擇一個標準基礎\{e_j\}_{j=1}^M { e j } M j = 1 。因此,每個向量v_i v i都可以唯一地寫成
$$ v_i = \sum_{j=1}^M a_{ij} e_j, $$
對於某些標量a_{ij} \in \mathbb{F}_p a i j ∈ F p 。對於每個向量v_i v i ,我們都有一個 Pedersen 承諾
$$ C_i = \sum_{j=1}^M a_{ij}G_j \in E. $$
最後,對於大小為D \sim 40 D ∼ 40 的子集中的每個對等體,提議者均勻隨機地選擇一組標量b_i b i , i=1, ...,N i = 1 , . . . , N ,並將以下信息發送給對等體
- 向量v = \sum_{i=1}^N b_i v_i \in \mathbb{F}_p^M v = ∑ N i = 1 b i v i ∈ F M p 。其大小為32M 32 M字節,是消息的內容。
- N N 個承諾C_i C i , i=1,...,N i = 1 , ... , N 。這是32N 32 N個字節。
- N N個係數b_i b i , i=1, ...,N i = 1 , . . . , N 。這是32N 32 N個字節。
- 對N N 個承諾的哈希值進行 BLS 簽名C_1 || C_2 || ... || C_N C 1 | | C 2 | | . . . | | C N ,這是96 96 個字節。
簽名消息是上述 1-4 項元素的集合。我們看到每條消息中都有64N \sim 640 64 N ∼ 640 個額外字節作為 sidecar 發送。
接收對等體
當對等方收到上一節中的消息時,驗證過程如下
- 它驗證簽名對於提議者和接收承諾的哈希值是否有效。
- 它寫入接收向量v = \sum_{j=1}^M a_j e_j v = ∑ M j = 1 a j e j然後計算 Pedersen 承諾C = \sum_{j=1}^M a_j G_j C = ∑ M j = 1 a j G j 。
- 收到的係數b_i b i聲明v = \sum_{i=1}^N b_i v_i v = ∑ N i = 1 b i v i 。對等方計算C'= \sum_{i=1}^N b_i C_i C ′ = ∑ N i = 1 b i C i ,然後驗證C = C' C = C ′ 。
對等方會跟蹤它們已收到的消息,假設它們是向量w_i w i , i = 1,...,L i = 1 , . . . , L (其中L < N L < N ) 。它們生成一個子空間W \subset \mathbb{F}_p^M W ⊂ F M p 。當它們收到v v時,它們首先檢查該向量是否在W W中。如果是,則它們將其丟棄,因為該向量已經是前幾個向量的線性組合。該協議的關鍵在於這種情況不太可能發生(對於上述數字,發生這種情況的概率遠小於2^{-256} 2 − 256 )。作為此的推論,當節點已收到N N 條消息時,它就知道可以從消息w_i w i , i=1,...,N i = 1 , . . .中恢復原始v_i v i ,從而恢復塊。 , N .
還要注意,只需要一次簽名驗證,所有傳入消息都具有相同的承諾C_i C i和同一組承諾上的相同簽名,因此對等方可以緩存第一次有效驗證的結果。
發送對等體
對等節點在收到一個塊後,可以立即將塊發送給其他對等節點。假設一個節點持有w_i w i , i=1,...,L i = 1 , . . . , L ,其中L \leq N L ≤ N ,如上一節所述。節點還會跟蹤它們收到的標量係數,因此它們知道它們持有的塊滿足
$$ w_i = \sum_{j=1}^N b_{ij} v_j \quad \forall i,$$
對於某些標量b_{ij} \in \mathbb{F}_p b i j ∈ F p,它們保存在內部狀態中。最後,節點還保留完整的承諾C_i C i和提議者的簽名,這些簽名是在它們驗證收到的第一個塊時驗證的。
節點發送消息的流程如下。
- 它們隨機選擇L L 個標量\alpha_i \in \mathbb{F}_p α i ∈ F p , i=1,...,L i = 1 , . . . , L 。
- 它們形成塊w = \sum_{i=1}^L \alpha_i w_i w = ∑ L i = 1 α i w i 。
- 它們形成N N 個標量a_j a j , i=1,...,N i = 1 , . . . , N ,其公式為
$$ a_j = \sum_{i=1}^L \alpha_i b_{ij}, \quad \forall j=1,…,N. $$
他們發送的消息由塊w w 、係數a_j a j和帶有提議者簽名的承諾C_i C i組成。
基準
該協議有一些與 gossipsub 相同的組件,例如提議者需要製作一個 BLS 簽名,驗證者必須檢查一個 BLS 簽名。我們在此記錄了除通常的 gossipsub 操作之外需要執行的操作的基準。這些是協議對節點的 CPU開銷。基準測試已在 Macbook M4 Pro 筆記本電腦和 Intel i7-8550U CPU @ 1.80GHz 上進行。
這些基準測試的參數為N=10 (塊數為N = 10) ,總塊大小為 118.75KB。所有基準測試都是單線程的,都可以並行化
提議者
提議者需要履行N N Pedersen 承諾。這被基準化為
| 定時 | 模型 |
|---|---|
| [25.588 毫秒 25.646 毫秒 25.715 毫秒] | 蘋果 |
| [46.7毫秒 47.640毫秒 48.667毫秒] | 英特爾 |
節點
接收節點需要計算每個塊的 1 個 Pedersen 承諾,並執行提議者提供的承諾的相應線性組合。這些操作的時間如下
| 定時 | 模型 |
|---|---|
| [2.6817 毫秒 2.6983 毫秒 2.7193 毫秒] | 蘋果 |
| [4.9479 毫秒 5.1023 毫秒 5.2832 毫秒] | 英特爾 |
發送新塊時,節點需要對現有塊進行線性組合。這些操作的時間如下
| 定時 | 模型 |
|---|---|
| [246.67 微秒 247.85 微秒 249.46 微秒] | 蘋果 |
| [616.97 微秒 627.94 微秒 640.59 微秒] | 英特爾 |
在接收N 個區塊後解碼整個區塊時,節點需要求解線性方程組。時間如下
| 定時 | 模型 |
|---|---|
| [2.5280 毫秒 2.5328 毫秒 2.5382 毫秒] | 蘋果 |
| [5.1208 毫秒 5.1421 毫秒 5.1705 毫秒] | 英特爾 |
總體 CPU 開銷。
Apple M4 上提議者的總開銷為 26ms(單線程),而接收節點的總開銷為 29.6ms(單線程)。這兩個過程都是完全可並行的。對於提議者來說,它可以並行計算每個承諾,而對於接收節點來說,這些自然是並行事件,因為該節點正在從不同的對等節點並行接收塊。在 Apple M4 上並行運行這些過程會導致提議者端為 2.6ms,接收對等節點為 2.7ms。對於實際應用來說,與所涉及的網絡延遲相比,將這些開銷視為零是合理的。
優化
一些未實施的過早優化包括在塊到來時反轉線性系統,儘管上面引用的概念證明確實將傳入的係數矩陣保持在 Eschelon 形式。最重要的是,消息的隨機係數不需要在像 Ristretto 場這樣大的場中。像\mathbb{F}_{257} F 257這樣的小素數場就足夠了。然而,由於 Pedersen 承諾發生在 Ristretto 曲線中,我們被迫在更大的域中執行標量運算。這些基準的實現為線性組合選擇了較小的係數,並且這些係數在每次跳躍中都會增長。通過正確控制和選擇隨機係數,我們可能能夠將線性系統的係數(以及發送塊的帶寬開銷)限制為 4 個字節而不是 32 個字節進行編碼。
執行此類優化的最簡單方法是對定義在\mathbb{F}_q F q上的橢圓曲線進行操作,其中q = p^r q = p r是某個小素數p p 。這樣就可以在子域\mathbb{F}_p \subset \mathbb{F}_q F p ⊂ F q上選擇係數。
隱私考慮上面鏈接的 PoC 中的實現認為每個節點(包括提議者)都會選擇較小的係數來合成其線性變換。這允許接收具有較小系數的塊的對等方識別該塊的提議者。要麼採用上述優化,通過執行類似 Bareiss 擴展的算法來保持所有係數較小,要麼我們應該允許提議者從字段\mathbb{F}_p F p中選擇隨機係數。
模擬
我們在以下一些簡化的假設下對塊傳播進行了模擬。
- 我們選擇一個隨機網絡,將其建模為有向圖,其中有 10000 個節點,每個節點有D D個對等點可以向其發送消息。D D在本文中稱為網格大小,其範圍從 3 到 80,變化範圍很大。
- 在完整節點集上隨機且統一地選擇對等點。
- 每個連接都選擇相同的帶寬X X MBps(在以太坊中通常假設為X=20 ,但我們可以將此數字保留為參數)
- 每次網絡跳躍都會產生額外的恆定延遲L L毫秒(通常以L=70 L = 70來衡量,但我們可以將此數字保留為參數)
- 假設該消息大小總計為B B KB。
- 對於使用 RLNC 的模擬,我們使用N= 10個塊來劃分塊。
- 每次一個節點向另一個節點發送消息,而該節點由於冗餘而丟棄該消息(例如,該節點已經有完整的塊),我們將該消息的大小記錄為浪費的帶寬。
八卦子
我們使用了D= 6個節點來發送消息。我們得到網絡平均需要 7 跳才能將整個區塊傳播到 99% 的網絡,總傳播時間為
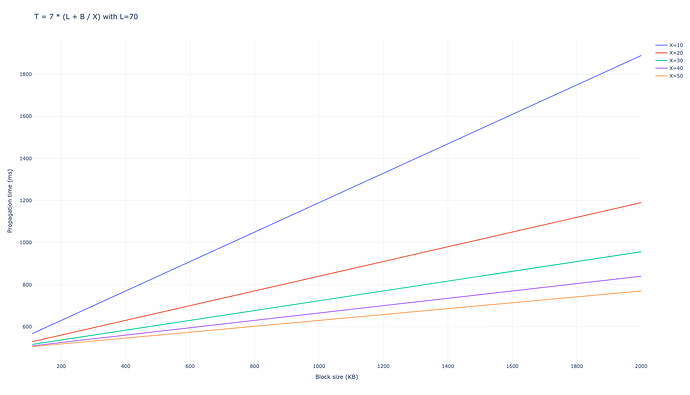
$$ T_{\mathrm{gossipsub, D=6}} = 7 \cdot (L + B/X), $$
以毫秒為單位。
當D=8 時,結果類似
$$ T_{\mathrm{gossipsub, D=8}} = 6 \cdot (L + B/X), $$
當D=6 D = 6時,浪費的帶寬為94,060 \cdot B 94 , 060 ⋅ B ;當D=8 D = 8 時,浪費的帶寬為100,297 \cdot B 100 , 297 ⋅ B。
對於較低的B B值,比如當前的以太坊區塊,延遲決定了傳播;而對於較大的值,例如在對等 DAS 之後傳播 blob,帶寬成為主要因素。
遠程控制網絡中心
每個對等體單個塊
通過隨機線性網絡編碼,我們可以使用不同的策略。我們模擬了一個系統,其中每個節點只會向其大小為D的網格中的所有對等點發送單個塊,這樣我們就可以保證產生的延遲與 gossipsub 中的相同:每跳的單次延遲成本為L L毫秒。這要求網格大小遠遠大於塊數N N 。請注意,對於大小為D_{gossipsub} D g o s s i p s u b的 gossipsub 網格(例如當前以太坊中的8 8 ),我們需要設置D_{RLNC} = D_{gossipsub} \cdot N D R L N C = D g o s s i p s u b ⋅ N以消耗每個節點相同的帶寬,根據當前值,這將是80 80 。
採用更保守的帶寬一半的值,即D=40 D = 40,我們得到
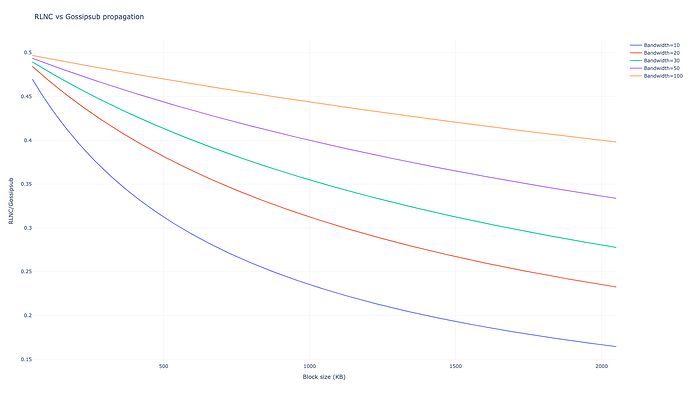
$$T_{RLNC, D=40} = 4 \cdot \left(L + \frac{B}{10 X} \right), $$
浪費的帶寬為29,917\cdot B 29 , 917 ⋅ B 。假設帶寬與今天相同,我們通過D=80獲得D = 80,我們得到了令人印象深刻的
$$T_{RLNC, D=80} = 3 \cdot \left(L + \frac{B}{10 X} \right), $$
浪費的帶寬為28,124\cdot B 28 , 124 ⋅ B ,相當於 gossipsub 中相應浪費帶寬的 28%。
差異
對於每個節點發送的相同帶寬,我們發現傳播時間不同,一方面是因為延遲減半(有 3 個跳數 vs. 6 個跳數),另一方面是因為塊傳播速度更快,每單位時間消耗的帶寬是原來的十分之一。此外,多餘消息浪費的帶寬被削減到 gossipsub 浪費消息的 28%。傳播時間和浪費的帶寬也得到了類似的結果,但每個節點發送的帶寬減少了一半。
在較低的塊大小端,延遲占主導地位,gossipsub 上的 3 跳與 6 跳是主要區別,而在較高的塊大小端,帶寬性能占主導地位。對於更大的塊大小,RLNC 中的 CPU 開銷會變得更糟,但考慮到傳輸時間的數量級,這些可以忽略不計。
每個對等體有多個塊
在生產中的每個對等點單塊方法中,具有更高帶寬的節點可以選擇向更多對等點廣播。在節點級別,這可以通過簡單地向所有當前對等點廣播來實現,節點運營商只需通過配置標誌選擇對等點數量即可。另一種方法是允許節點按順序向單個對等點發送多個塊。這些模擬的結果與上面的完全相同,但是 D比預期的要低得多。例如當D=6時,如果每個對等點發送一個塊,則永遠不會廣播完整的塊。模擬需要 10 次跳轉才能廣播完整的塊。當D = 10時,跳數減少到 9。
結論、遺漏和進一步的工作
我們的結果表明,如果我們在當前路由協議上使用 RLNC,那麼每個節點的塊傳播時間和帶寬使用率都會有顯著改善。塊/blob 大小越大或每跳延遲成本越短,這些好處就越明顯。此協議的實施需要對當前架構進行重大更改,並且可能需要全新的 pubsub 機制。為了證明這一點,我們可能希望實現完整的網絡堆棧以在Shadow下進行模擬。另一種方法是實現 Reed-Solomon 擦除編碼和路由,類似於我們對 Peer-DAS 所做的。將上述模擬擴展到這種情況應該很簡單,但op. cit已經包含了許多這樣的比較。