這篇文章的第二部分討論了StableSwap不變數。

CryptoSwap

CryptoSwap不變數是一個核心數學公式,它定義了Curve交易池的"流動性曲線",專門設計用於高度波動的資產對(不像穩定幣那樣緊密掛鉤)。它有助於池集中流動性在"內部"價格(透過內部預言機確定)周圍,並在池失衡時自動調整。以下是關鍵要點:

結合兩種不變數的優勢:

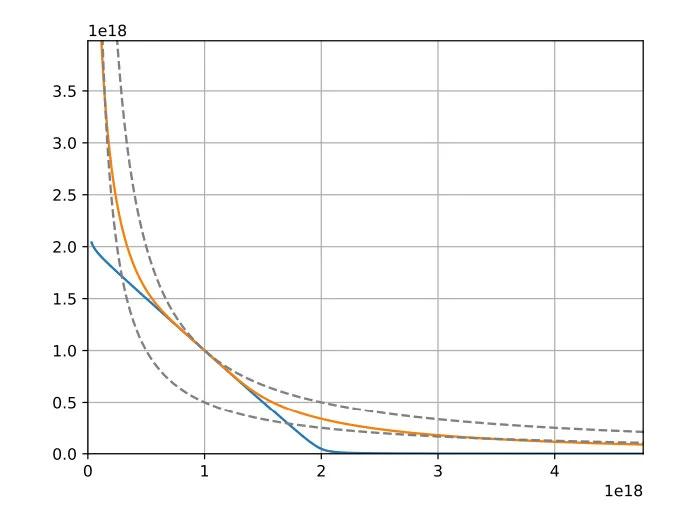
• 當池平衡(價值等價餘額)時,CryptoSwap不變數的行為類似於StableSwap不變數,創造一個"平坦"區域(無滑點),實現近1:1的交換。

• 當池失衡時,不變數逐漸轉向恆定乘積不變數行為(如Uniswap),導致滑點增加,並保護池免受過度價格偏離。

在第1部分中,StableSwap不變數描述在一般公式中:

CryptoSwap不變數由StableSwap不變數鼓勵:

但是,K的定義略有不同:

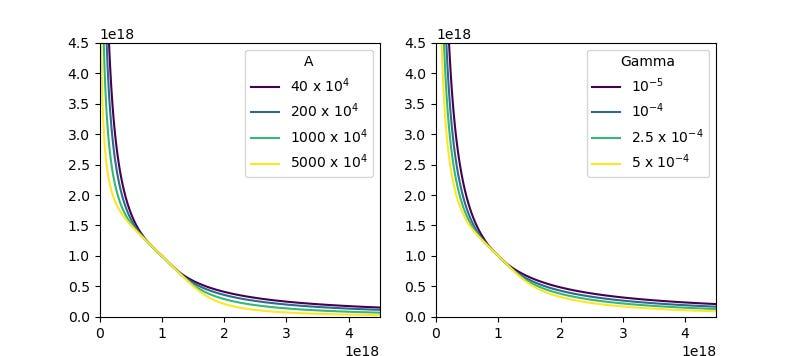
• A(放大係數):A引數類似於StableSwap不變數(Curve v1),控制曲線中心的平坦程度。這決定了流動性在預期匯率(即"價格尺度")周圍的集中程度。

• Gamma:Gamma引數控制上圖中兩條恆定乘積曲線的分離程度(虛線)。當Gamma增加時,它會將"調整後的恆定乘積"曲線拉向左下角,使曲線的漸近線更靠近座標軸,並擴大整體曲線形狀。

初始化:

使用初始公式,我們可以將f(D_0)重寫為只有2枚代幣的情況:

使用牛頓法,初始值可以轉換為:

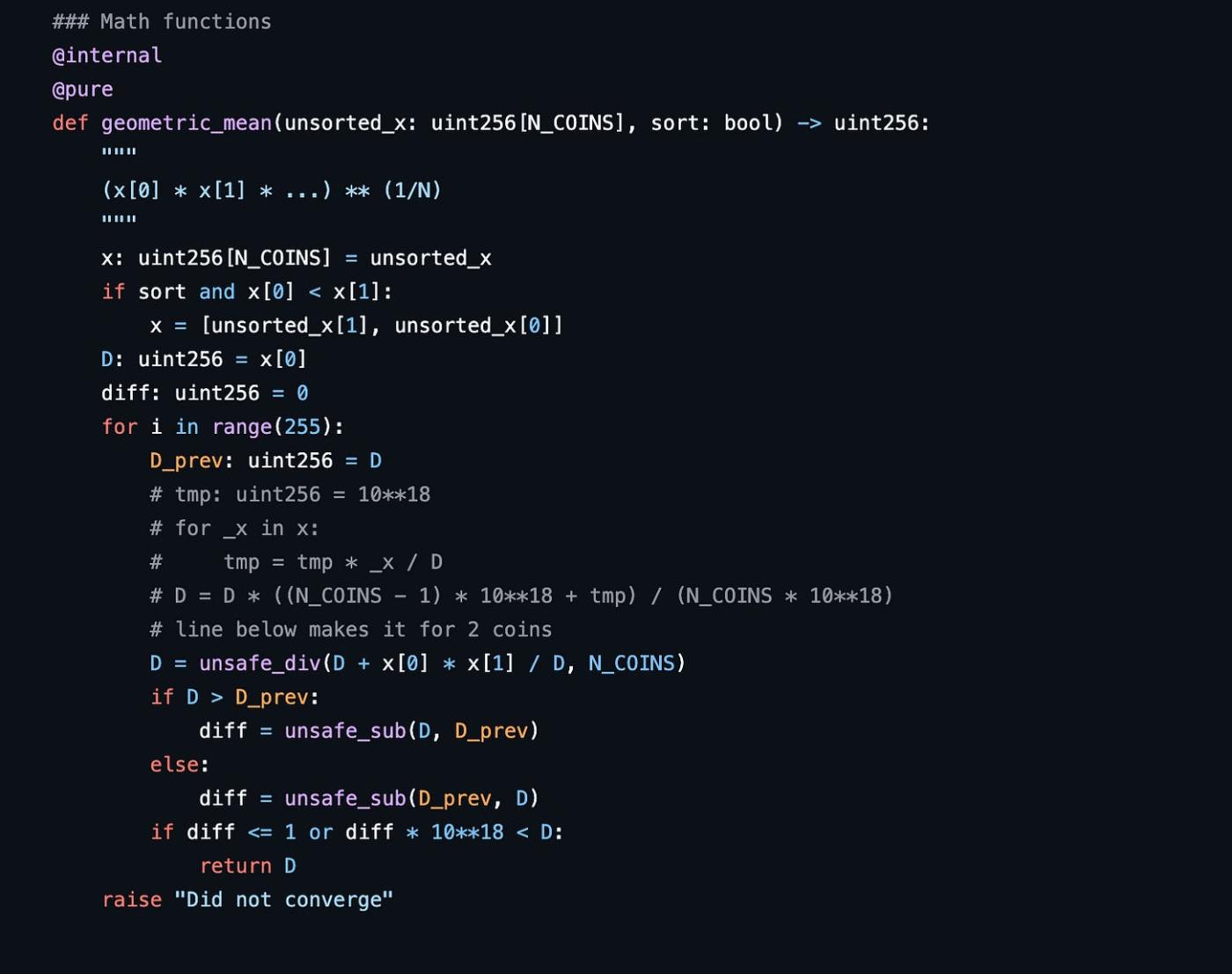
使用此公式,可以透過迴圈A次來計算D_0。在Viper程式碼中,A設定為255。

該程式碼計算當前和上一個D_0值之間的絕對差異。當差異非常小(diff ≤ 1)或當差異乘以10^18小於D_0時,它會停止迭代。滿足其中一個條件後,該函式返回收斂的D_0值。

回到不變數,令S為x_i之和,P為x_i之積。對於2枚代幣(N = 2),f(D)變為:

f(D)的導數為:

這可以轉換為:

上述公式可以簡化。首先,將所有項除以K,並展開括號內的所有內容。

現在S可以寫為- S + 2S:

然後,提取包含S和D的組中的公共項。

使所有分母在括號內通用:

引入兩個輔助變數mul1和mul2來簡化函式中的變數:

現在,導數f'(D)可以簡化為:

在Viper程式碼中,_g1k0變數被定義為:

回到程式碼中,

這段程式碼計算-f'(D)而不是f'(D)。這使牛頓步驟更加清晰。此外,f(D)被除以K:

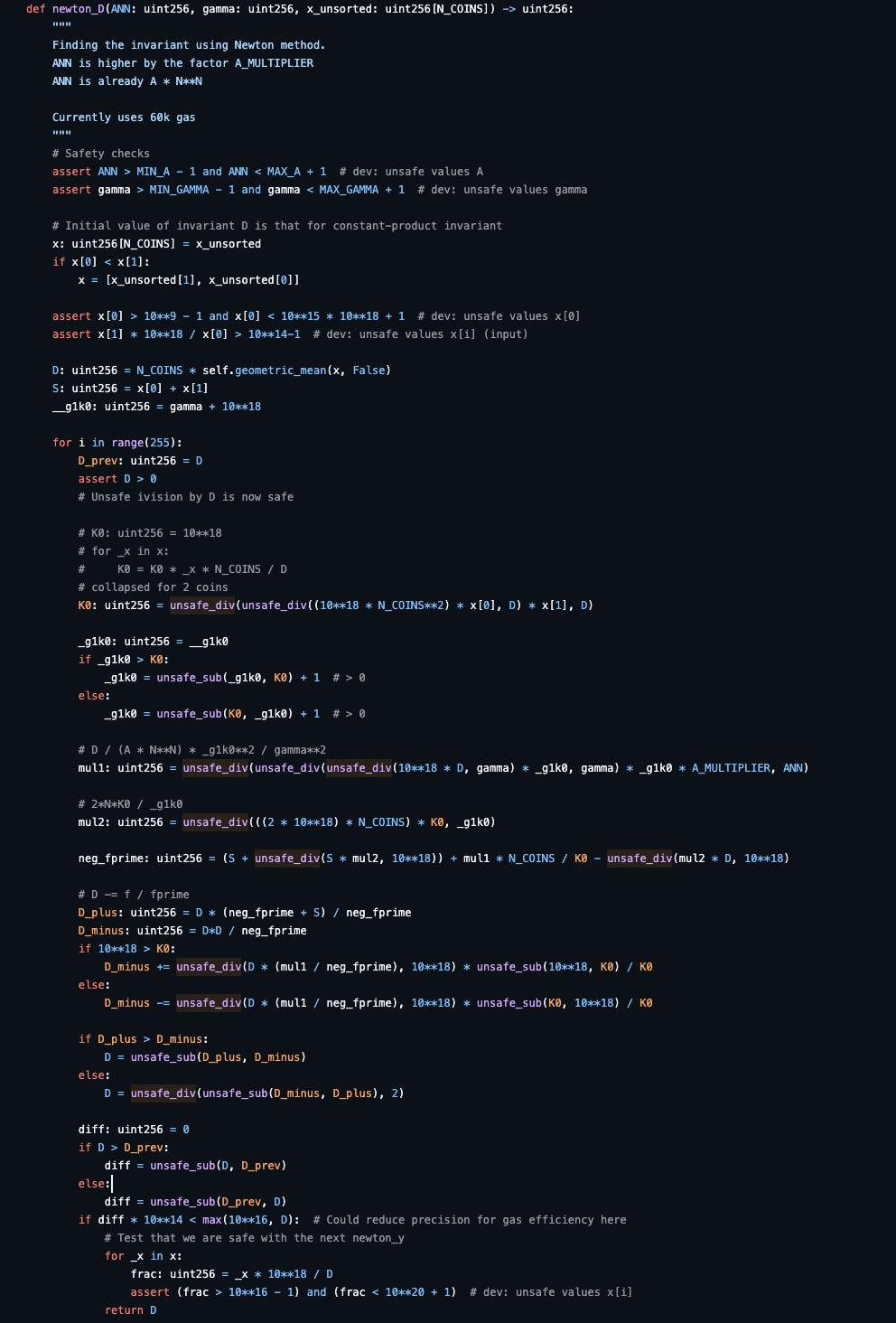
現在,D的完整牛頓法為:

該公式已分為兩部分用於牛頓法:

最終的D將計算為上述兩個方程的差。