基於格的簽名聚合
這是 David Nevado、Dohoon Kim 和 Miha Stopar 的聯合報告。
在以太坊的權益證明 (PoS) 中,BLS 簽名用於將來自多個驗證者的證明聚合成一個緊湊的簽名。然而,BLS 並不具備量子安全性,在後量子時代,它將需要被取代。一個有前景的方向是基於格 (Lattice) 的聚合,例如最近發表的《使用 LaBRADOR 聚合 Falcon 簽名》 (Aggregating Falcon Signatures with LaBRADOR) ,該論文探索瞭如何在保持小規模和快速驗證的同時,高效地聚合後量子 Falcon 簽名。
雖然 LaBRADOR 提供了一種很有前景的方法來聚合 Falcon 簽名和緊湊證明(10,000 個簽名約 74 KB),但也存在其他後量子替代方案。其中一種方法是使用 STARK,在零知識證明的情況下證明許多基於哈希的簽名是有效的。這些方法通常會導致更大的證明大小( 10,000 個簽名約 300 KB) ,但其優勢在於更快的驗證時間。
在本文的最後,我們將 LaBRADOR 方法與最近提出的基於哈希的簽名聚合方法進行了比較。在後者方案中,簽名使用 Poseidon2 實例化,而聚合則依賴於基於 Merkle 樹的多項式承諾方案的 Keccak。聚合本身包括在 Plonk 風格的證明系統中對簽名驗證器進行算術運算。
LaBRADOR 是一個相對較新的協議,其實現支持仍然有限。雖然一些 Rust 實現正在湧現,但它們尚未成熟,因此目前主要使用原始的 C 語言參考代碼。為了進行基準測試,我們使用了 Lazer 代碼庫中的agg_sig.py腳本,該腳本封裝了LaBRADOR 的 C 語言實現。下文中,我們首先展示一些基準測試結果,然後解釋 Lazer 方法與原始論文《使用 LaBRADOR 聚合 Falcon 簽名》中描述的方法有何不同。
績效結果
方法:
我們使用了LaBRADOR 的 fork 版本,其中包含一些修改,以支持更大的簽名批次(超過 2,000 個簽名)。這些修改是為了能夠將模量增加到大約2^{48} 2 48 ,從而處理聚合過程中出現的較大中間值。
結果:
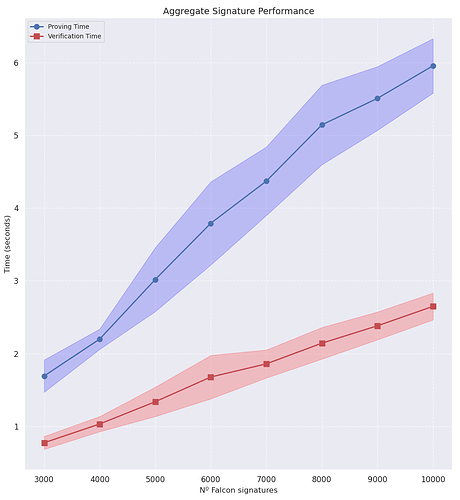
我們測量了 3,000 到 10,000 個 Falcon-512 簽名批次聚合的驗證時間。基準測試基於在11th Gen Intel(R) Core(TM) i5-11400H @ 2.70GHz處理器上進行單線程執行獲得。
| # 簽名 | 檢驗時間(秒) | 驗證時間(秒) | 證明大小 |
|---|---|---|---|
| 3000 | 1.6921±0.2220 | 0.7739±0.0888 | 77.83 千字節 |
| 4000 | 2.1991±0.1403 | 1.0321±0.1044 | 69.82 千字節 |
| 5000 | 3.0182±0.4394 | 1.3380±0.2021 | 72.45 千字節 |
| 6000 | 3.7914±0.5716 | 1.6779±0.2989 | 72.11 千字節 |
| 7000 | 4.3709±0.4716 | 1.8586±0.1928 | 71.83 千字節 |
| 8000 | 5.1447±0.5469 | 2.1430±0.2175 | 74.02 千字節 |
| 9000 | 5.5085±0.4382 | 2.3821±0.1915 | 72.27 千字節 |
| 10000 | 5.9565±0.3750 | 2.6492±0.1848 | 74.07 千字節 |
注意:雖然圖表中未顯示,但此配置支持更大的簽名批次。較小的批次(<2,000 個簽名)可實現更佳性能,因為模量可以減小至2^{40} 2 40 ,從而縮短證明/驗證時間並減少證明大小。
重點:
10k Falcon-512 簽名可以與 LaBRADOR 聚合,從而產生:
- 74.07KB證明大小。
- 5.95秒證明生成。
- 2.65s證明驗證。
從結果來看,驗證時間是採用的最大障礙。我們對驗證進行了分析,以提高其性能。
驗證細目
Falcon 簽名的聚合是使用打包證明和 LaBRADOR 庫提供的 Dachshund 前端(有關 Dachshund 的簡要描述,請參閱Lazer 論文)進行的。我們對 Dachshund 測試中的驗證過程進行了性能分析,以找出瓶頸和潛在的優化機會。雖然我們嘗試通過並行化來縮短原始驗證時間,但這些努力並未成功。
分析
打包證明的驗證需要1.2510秒,發生在composite_verify_simple中,該過程包含兩個步驟:
- simple_reduce :從簡單語句
st和證明p導出原始複合語句tst(1.1356 秒,約佔總時間的 90%)。 - Composite_verify :根據
tst驗證p(剩餘 10%)。
鑑於其主導地位,我們專注於優化simple_reduce 。
simple_reduce分析
對於 48 位模數,常數LIFTS LIFTS = 3循環消耗了77% 的運行時間,但其順序依賴性(由於 Fiat-Shamir 挑戰)阻礙了並行化。
| 功能 | 時間(秒) | 總運行時間的百分比 |
|---|---|---|
init_statement() + betasq | 0.0000 | 0.00% |
reduce_simple_commit() | 0.0000 | 0.00% |
reduce_project() | 0.0451 | 3.97% |
init_constraint() | 0.0000 | 0.00% |
| LIFTS 循環 (3x) | 0.8800 | 77.50% |
free_constraint() + 清理 | 0.0016 | 0.14% |
simple_aggregate() | 0.1067 | 9.40% |
aggregate_sparsecnst() | 0.0969 | 8.53% |
reduce_amortize() | 0.0053 | 0.47% |
| 全部的 | 1.1356 | 100% |
在循環中,我們發現了幾個可以優化的函數,特別是collaps_jlproj_raw() 。
LIFTS 循環細分(每次迭代)
| 功能 | 平均時間(秒) | 總運行時間的百分比 |
|---|---|---|
collaps_jlproj_raw() | 0.1166 | 10.27% |
polxvec_setzero() | 0.0178 | 1.57% |
simple_collaps() | 0.0537 | 4.73% |
reduce_lift_aggregate_zqcnst | 0.1053 | 9.27% |
| 總計(每次迭代) | 0.2934 | 25.84% |
| 總計(3 次迭代) | 0.8802 | 77.51% |
優化嘗試
LaBRADOR 已針對 AVX-512 指令進行了大量優化,但仍保持單線程運行。我們探索了並行化,但遇到了一些挑戰:
菲亞特-沙米爾依賴關係:
FS 挑戰的推導不可避免地是連續的,這限制了並行化的機會。矩陣運算:
使用 OpenMP 並行化polxvec_jlproj_collapsmat(simple_reduce的 30%)會導致性能下降,可能是因為:- 錯誤共享(緩存行的線程爭用)。
- 內存帶寬飽和(AVX-512 已達到最大帶寬)。
然而,需要進一步分析來找出根本原因。
比較:Lazer 和使用 LaBRADOR 聚合獵鷹信號
乍一看,使用 LaBRADOR 聚合獵鷹特徵的技術似乎與 Lazer 的技術有很大不同,但事實並非如此。
讓我們首先觀察 Falcon 簽名的聚合是如何工作的,然後深入研究兩種方法之間的差異。
獵鷹簽名
Falcon 簽名由(s_1, s_2) ( s 1 , s 2 )組成,因此:
其中\mathbf{h} h是公鑰的一部分, \mathbf{t} t是消息的哈希值。
我們正在使用除q q之外的其他模數的證明系統來證明\mathbf{s}_1 s 1和\mathbf{s}_2 s 2的知識,因此該等式被重寫為:
對於某個多項式\mathbf{v} v 。
Falcon 簽名的聚合
我們希望聚合N N Falcon 簽名,這意味著證明:
其中i=1,..., N . i = 1 , ... , N .
注意, q q是 Falcon 方案中的模量,且方程需要在R_{q'} R q ′中成立,其中q' > q q ′ > q ,但環度d. d相同。為了證明等式在R. R上成立,方程中不能出現環繞模q' q ′ 。
論文《使用 LaBRADOR 聚合 Falcon 簽名》使用LaBRADOR作為證明系統。在論文提交時,由於下文所述的問題,LaBRADOR 的使用受到了一些額外的限制。LaBRADOR 源代碼及其 Dachshund 前端後來發佈,事實上,Dachshund 前端直接解決了最初阻礙 LaBRADOR 正常使用的問題。
問題 1:規範檢查
在 LaBRADOR 中,使用約翰遜-林登斯特勞斯投影進行範數檢驗是一種近似方法,並且一次性應用於所有見證向量。這種方法在 LaBRADOR 源代碼中被稱為“吉娃娃前端”。相比之下,“臘腸犬前端”則對每個見證向量分別執行範數檢驗。回想一下,在簽名聚合的上下文中,我們有多個見證向量: \mathbf{s}_{i,1} s i , 1和\mathbf{s}_{i,2} s i , 2 。
由於 Dachshund 尚未發佈,本文假設使用 Chihuahua 前端。該前端證明了整個見證(即所有見證向量的總和)的範數很小——這種方法適用於某些應用。
Johnson–Lindenstrauss 投影的思路是使用隨機投影矩陣\Pi Π :對於見證\mathbf{s} s ,計算投影\Pi \mathbf{s} Π s (矩陣向量乘法),驗證者直接計算投影向量的範數。有一個引理粗略地指出,如果投影很小,則原始向量也很小:如果|\Pi \mathbf{s}|_2 \leq \sqrt{30} b | Π s | 2 ≤ √ 30 b ,其中b為某個邊界b ,則|\mathbf{s}|_2 \leq b | s | 2 ≤ b 。還必須滿足\sqrt{\lambda} b \leq \frac{q}{C_1} √ λ b ≤ q C 1安全級別為\lambda λ和某個常數C_1 C 1 。這對聚合方案中使用的模量q q施加了約束——這也是本文使用更大模量q' > q q ′ > q而不是 Falcon 原始模量q q的原因之一。
然而,在簽名聚合的情況下,需要證明每個見證向量(例如\mathbf{s}_{i,1} s i , 1和 $\mathbf{s}_{i,2}$)的較小性,而這正是 Dachshund 算法的設計初衷。由於 Dachshund 算法尚未面世,本文作者引入了額外的顯式約束,以強制對各個見證向量施加範數界限。本文仍然使用了約翰遜-林登斯特勞斯投影,但目的不同:防止模迴繞。下文我們將總結顯式範數約束以及約翰遜-林登斯特勞斯投影在防止模迴繞方面的應用。
個體見證向量範數約束
證明||\mathbf{s}_{i,1}||^2_2 + ||\mathbf{s}_{i,2}||^2_2 \leq \beta^2 | | s i , 1 | | 2 2 + | | s i , 2 | | 2 2 ≤ β 2等價於證明\beta^2 - ||\mathbf{s}_{i,1}||^2_2 - ||\mathbf{s}_{i,2}||^2_2 β 2 − | | s i , 1 | | 2 2 − | | s i , 2 | | 2 2為非負數。
拉格朗日四平方定理指出,任何非負整數都可以寫成四個平方和。因此,我們可以找到四個整數\epsilon_{i,0}, \epsilon_{i,1}, \epsilon_{i,2}, \epsilon_{i,3} \in \mathbb{Z} ϵ i , 0 , ϵ i , 1 , ϵ i , 2 , ϵ i , 3 ∈ Z ,使得:
第i個簽名的\epsilon_{i,j} ϵ i , j值作為多項式的係數添加到見證中
請注意,多項式\mathbf{a} = a_0 + a_1 X + ... + a_{d-1} X^{d-1}, a = a 0 + a 1 X + . . . + a d − 1 X d − 1 ,我們可以計算其範數為(利用||\mathbf{a}||^2 = ct(\langle \mathbf{a}, \sigma_{-1}(\mathbf{a}) \rangle) | | a | | 2 = c t ( ⟨ a , σ − 1 ( a ) ⟩ ) ,其中共軛自同構\sigma_{-1} σ − 1和X^d = -1 X d = − 1 ):
我們表示\mathbf{a}' = a_0 - a_{d-1} X - ... - a_1 X^{d-1}. a ′ = a 0 − a d − 1 X − . . . − a 1 X d − 1 .
現在我們可以將範數約束重寫為 LaBRADOR 約束,如下所示:
但我們還需要檢查新的見證元素是否已正確構建,以及見證元素的係數是否足夠小,以至於它們不會環繞q'. q ′ 。
讓我們觀察如何表達一個約束,即多項式\mathbf{a} a的第 j j個係數是某個值,假設b: b :
對於每個\epsilon_i ϵ i ,我們需要準備約束以確保\epsilon_{i,4},..., \epsilon_{i, d-1} ϵ i , 4 , . . . , ϵ i , d − 1為零。
我們還需要確保\mathbf{s}'_{i,1} s ′ i , 1是從\mathbf{s}_{i,1} s i , 1正確構造的,例如:
對於\mathbf{s}_{i,2} s i , 2和\epsilon_i ϵ i也同樣如此。
與基於四個平方和的方法相反,Dachshund 使用以 2 為底的分解向量,並將其與帶有布爾係數的多項式相乘。性能上可能沒有顯著差異。
防止環繞
按照論文中的方法,需要確保以下兩個方程不會出現環繞現象:
事實證明,第一個更具限制性,我們得到:
從第二個方程我們得到:
為了確保這一點,我們使用了約翰遜-林登斯特勞斯投影法。
問題二:重塑證人
在簽名聚合方面,Chihuahua 前端的另一個限制是,由於需要計算大量所謂的垃圾多項式,因此在處理許多見證向量時效率低下。
證明器的運行時間——以及 LaBRADOR 收斂到基準情況的速度(即,壓縮證明大小需要多少個遞歸步驟)——取決於兩個關鍵參數:
- 多重性r r :見證向量的數量
- 秩n n :每個見證向量中的多項式數量
本文建議重塑見證人,以實現更加平衡的配置,目標是r = O(\sqrt{N}) r = O ( √ N )個秩為n = N的見證向量,其中N N是簽名的數量。
最初,見證由r = 2N 個向量組成(添加精確範數約束後數量會更多),每個向量的秩為 n = 1。這是一個高度不平衡的配置。為了提高 LaBRADOR 遞歸壓縮的效率,最好使r r和n n 的量級更接近。為了解決這個問題,該方案引入了一種填充策略:對見證進行重構,使得n \approx N n ≈ N且r \approx \sqrt{N} r ≈ √ N ,並根據需要用零填充新的見證向量。
然而,Dachshund 前端也解決了這個問題——Dachshund 旨在有效處理大量見證向量。
戒指選擇
另一個方面是環的選擇。雖然論文分析了多種方案,但最終採用了與 Lazer 相同的配置。多項式與幾個小素數p_i p i相乘(使用 NTT),然後使用顯式 CRT 模q q將結果合併。使用 16 位小素數p_i p i (介於2^{12} 2 12和2^{14} 2 14之間),完全拆分為\mathbb{Z}_r[X]/(X^{64} + 1) Z r [ X ] / ( X 64 + 1 ),可以實現高效的 Montgomery 算法(更多信息請參閱Greyhound 論文)。
概括
兩種簽名聚合方法(來自論文《使用 LaBRADOR 聚合 Falcon 簽名》和 Lazer 方法)非常相似,因此我們相信我們的基準(基於 Lazer 代碼)對兩者都相關。
基準測試中,基於格的簽名聚合方案最引人注目的特點是其證明大小,而其應用的最大障礙可能是驗證時間。使用多線程技術或許可以提高驗證性能,但這仍需要進一步研究。儘管如此,LaBRADOR 的作者們已經在對 LaBRADOR 協議及其 C 語言實現進行改進,預計這些改進將加快驗證速度——儘管目前很難量化具體提升幅度。
雖然驗證時間可能會隨著未來的優化而改善,但它可能無法與基於哈希的方法相匹配(見下表),其中驗證僅需幾毫秒。
| 公制 | LaBRADOR + Falcon(10000 個簽名,1 個線程) | 基於哈希(8192 個簽名,4 個線程) |
|---|---|---|
| 證明大小 | 74.07 千字節 | 1.7 MB(優化後目標約為 128 KB) |
| 驗證時間 | 5.95秒 | 5秒 |
| 驗證時間 | 2.65秒 | 106毫秒 |
| PQ 安全 | 是(基於晶格) | 是(基於哈希:Poseidon2 簽名,PCS 默克爾化中的 Keccak) |
| 並行化 | 有待探索 | 非常好——使用 4 個線程;幾乎線性擴展到 4,但超過 4 時效率較低 |
總而言之,LaBRADOR 方案似乎非常適合 Falcon 簽名聚合過程中出現的特定約束。為了縮短驗證時間,探索類似於Dory 的委託技術可能是一個有前景的方向。這些協議降低了驗證者的複雜性,在證明量較大但驗證者資源受限的場景中尤其具有吸引力。