離開學術界後，我曾承諾自己不再寫論文。但危急時刻，不得不採取非常措施！ 一個LVR問題困擾了我好幾年。後來@MartinTassy解決了這個問題。 以下是一些歷史和一些直覺 1/n

當@jason_of_cs、@ciamac、@Tim_Roughgarden 和 @alz_zyd_ 首次提出 LVR 的概念時，他們使用的是不含掉期費的模型。 這當然立即引發了一個問題：在包含掉期費的模型中，*淨* LVR 會是多少？ 2/n moallemi.com/ciamac/papers/lvr...

我邀請了兩位朋友（加州大學伯克利分校的 Dmitry Livdan 和高等經濟大學的 Alex Boulatov）來證明以下結論。 流動性提供者的損失： * 波動率的三次方 * 與交換費成反比 * 與區塊時間的平方成正比 然而，仍然存在兩個問題…… 3/n

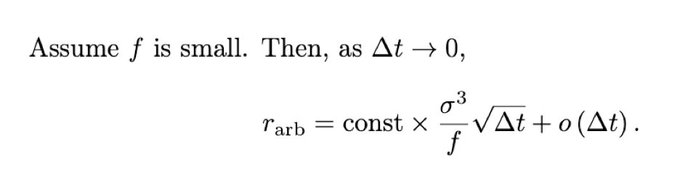
首先，我們的證明有點牽強（有點像福克-普朗克方程），至少我是這麼理解的。 其次，我找不到使這個方程成立的確切常數。 所以我很自然地放棄了，轉而發了一條推特。 4/n

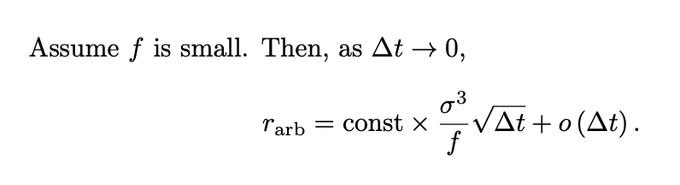
但隨後@jason_of_cs、@ciamac 和 @Tim_Roughgarden 發表了他們的“帶費用的 LVR”文章，其中除其他內容外，還包含： * 帶費用模型中 LP 損失的精確公式 * 結果的完整證明 他們做到了…… 5/n moallemi.com/ciamac/papers/lvr...

一個優雅的假設：區塊的到達遵循泊松過程。 這個假設適用於工作量證明鏈。但大多數權益證明鏈的出塊時間都是固定的。 這讓我思考：如果平均出塊時間保持不變，那麼…… 6/n

區塊時間不確定性對套利者LP損失的影響？ 基本上，我們仍然需要確定那個常數！ 我鎖定了。我不再給孩子們讀書。取消了健身房會員資格。告訴朋友我的身體狀況不好。問了我認識的每一位統計學教授…… 7/n

然後我想起@MartinTassy和@_Dave__White_之前研究過類似的問題，但使用的工具略有不同。 （我儘可能在連續時間上進行計算，然後弄清楚在鄰近的離散模型中會發生什麼，但他們的方向相反。） 8/n

所以我聯繫了馬丁。 通過比較固定時間和泊松塊到達模型，可以清楚地看出一點。LP 的損失是以下因素的乘積： ARB掉期的概率 * 每次套利掉ARB的損失。 事實證明，套利掉ARB的*概率*... 9/n

只是*平均*出塊時間的函數。區塊是以固定間隔還是按照泊松模型到達並不重要。 但是，當出塊時間固定時，每次套利掉期的損失較小。為什麼？ 損失會隨著 CEX 價格的上漲而增加…… 10/n

在區塊間隔時間內，超過 DEX 的買賣價差。 要超過價差，CEX 價格首先需要達到價差的邊界，然後利用到下一個區塊的剩餘時間超過價差。 在泊松模型中，如果平均出塊時間為 12 秒…… 11/n

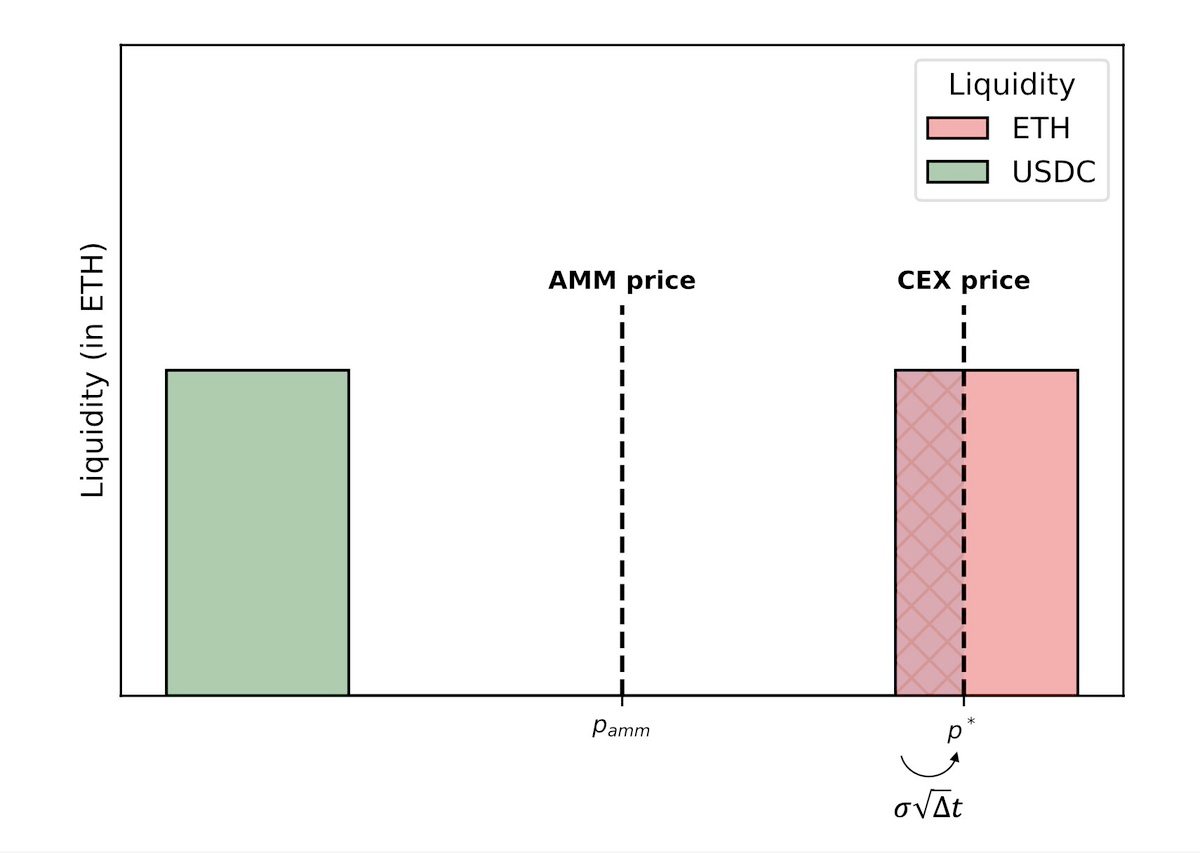
價格在前一個區塊生成後 2 秒達到邊界，那麼平均仍然需要 12 秒才能達到超調量。但如果區塊時間固定，則只需要 10 秒。 在下面的論文中，Martin 和我給出了固定區塊時間下損失的精確表達式。 12/n

事實證明，我們要尋找的常數包括在 1/2 處求值的黎曼 zeta 函數。 我覺得我們已經接近將AMM研究與黎曼假設聯繫起來了，考慮到一切都始於 xy=k，這非常令人印象深刻！ http:/arxiv.org/pdf/2505.05113