原文作者:Weikeng Chen

在以太坊虛擬機(EVM)中,Keccak 哈希函數廣泛用於狀態樹(Merkle Patricia Trees)的構造與驗證,佔據了零知識證明中的主要計算開銷。如何高效地對 Keccak 進行證明,是零知識證明領域長期未解的技術難題。
為應對這一挑戰,Polyhedra 團隊推出了 Binary GKR——一種專為 Keccak 及其他二進制操作設計的高性能證明系統。
核心進展:對 Keccak 的證明速度提升 5.7 倍
Binary GKR 實現了迄今為止最快的 Keccak 零知識證明性能,相比現有二進制證明系統最優解 FRI-Binius 提速約 5.7 倍。這一突破不僅在理論上具有重要意義,也為實際應用打開了新的可能性。
應用前景:zkEVM 的“通用加速側車”
我們認為,Binary GKR 可作為多種 zkEVM 架構中的“通用加速側車”,高效處理 Ethereum 狀態樹中大量的 Keccak 運算,從而顯著降低證明成本、提升系統吞吐與響應速度。
Polyhedra 將持續推動 Binary GKR 的產品化與開源進程,賦能以太坊及更廣泛生態中的 zk 架構升級。
Keccak:零知識以太坊的“聖盃”
以太坊正逐步向零知識證明原生的 Layer-1 演進。由 21 個團隊參與、涵蓋 22 種 ZK(E)VM 實現的 Ethproofs 計劃,正在嘗試對以太坊歷史區塊進行完整證明,邁出關鍵一步。
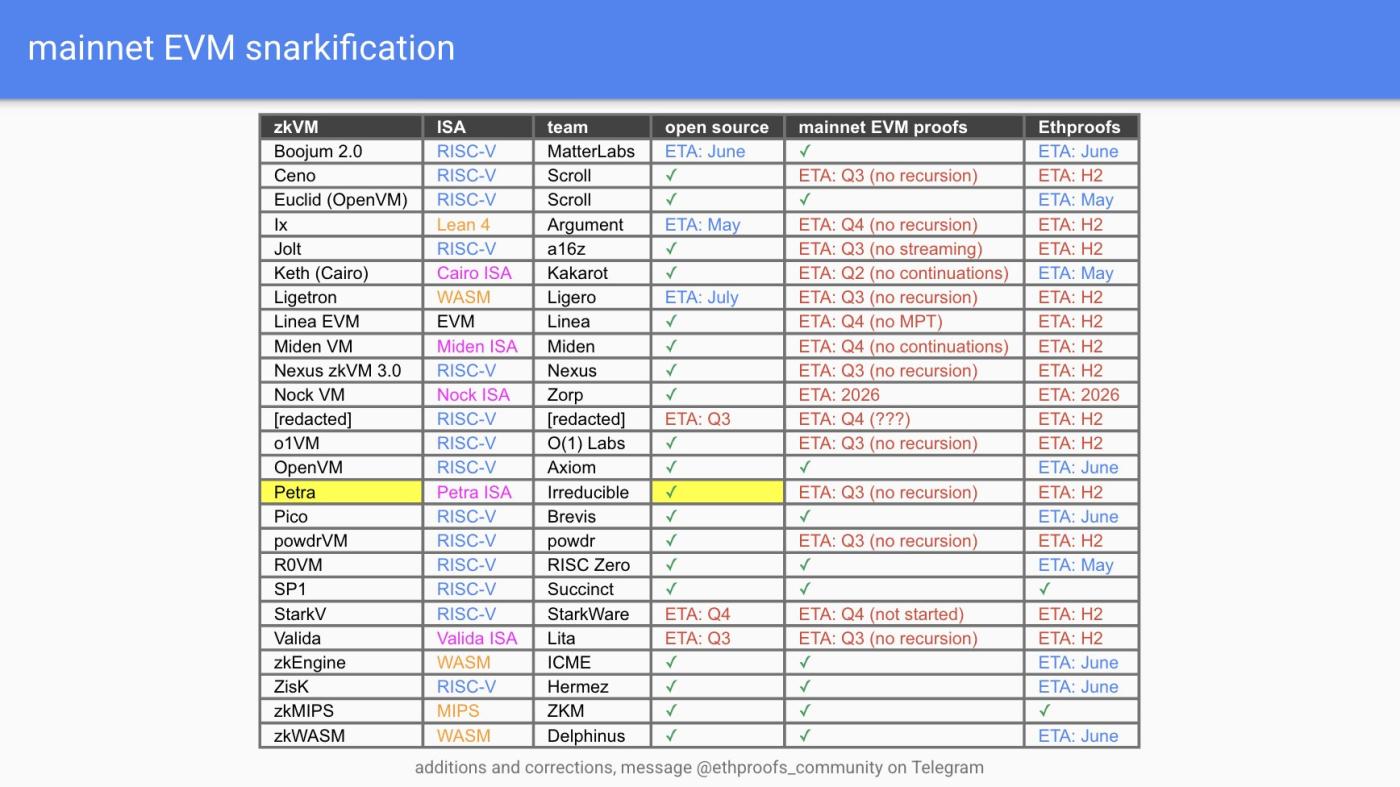
在 Ethproofs 官網 上可以實時查看多個團隊的進展:ZkCloud、Succinct、Snarkify 和 ZKM 等項目,已開始持續提交最新區塊的 ZK 證明。這一趨勢的最終目標,是將以太坊打造為以零知識證明驅動的執行層,而共識層僅需完成交易列表的提議等輕量任務。
zkEVM 架構面臨的最大挑戰:Keccak 的證明效率瓶頸
目前已有多個以太坊兼容 zkRollup 項目(如 Polygon、Taiko、Scroll)嘗試實現 zkEVM。然而,傳統 EVM 中一些在 CPU 上高效的操作,在零知識證明系統中卻代價高昂。其中最主要的性能瓶頸,正是 Keccak 哈希函數。
Keccak 被廣泛用於構建以太坊的 Merkle Patricia Tree,以哈希形式記錄全鏈狀態。然而 Keccak 的底層運算基於 位運算(bit-level operations),這與大多數 ZK 系統使用的 素數域(prime field)運算模型 並不兼容,從而導致性能顯著下降。
為了幫助理解 Keccak 哈希函數為何本質上是“位運算”的集合,我們在此簡要展示其中的五個核心操作:θ(theta)、ρ(rho)、π(pi)、χ(chi)和 ι(iota)。這些操作應用於一個 5 × 5 的矩陣結構,每個單元格為一個 64 位整數,我們稱之為“字”(word)。整個矩陣共包含 5 行 5 列。
θ(Theta):首先計算每一列的奇偶校驗值(parity),然後將該奇偶值與左側相鄰列進行異或運算(exclusive-or);同時,對右側相鄰列執行一次左旋轉(rotate-left)後,再進行異或。這一過程涉及基本的二進制操作,如“異或”與“左旋”。
ρ(Rho):對矩陣中的每一個字按位左旋轉,每個字的旋轉距離不同,但均為預設的固定值。該步驟完全由“左旋”操作構成。
π(Pi):根據固定模式重新排列矩陣中的字。由於該過程僅為位置置換,在零知識證明中通常被視為“零成本操作”。
χ(Chi):沿每一行進行按位組合操作,每個字會與該行中其左右相鄰的兩個字進行組合。該操作包括“異或”、“取反”(negation)與“與”(and)。
ι(Iota):將矩陣中第一個字與一個固定常數進行異或操作,僅涉及“異或”運算。
在零知識證明中實現 Keccak 的主要挑戰,正是如何有效表示這些位級操作,尤其是在每個操作都作用於 64 位整數的前提下。這也是我們稱其為 Keccak-1600 的原因——因為每一輪的狀態空間為 5 × 5 × 64 = 1600 位。而這樣的操作過程需重複 24 輪。
接下來,我們將簡要回顧一些此前實現 Keccak 的嘗試。
嘗試一:基於 Groth 16 或其他 R 1 CS 的證明系統
目前最流行且最直接的方式,是使用 Groth 16 或其他 R 1 CS(Rank-1 Constraint System)證明系統來實現 Keccak。為了在 Groth 16 中表達位運算,我們將每個位表示為 0 或 1 ,並通過算術關係來模擬如下邏輯運算:
異或(exclusive-or):使用表達式 a + b − 2 ab
取反(negation):使用表達式 1 − a(通常可無成本地融合進其他約束中)
與(and):使用表達式 a × b
而像“左旋”(rotate-left)和其他置換操作在 ZK 環境中通常被視為無成本操作,不需要額外約束。
根據計算,Keccak 每一輪中的約束數量如下:
θ 操作約產生 4480 個約束
ρ 與 π 操作為“零成本”
χ 操作約產生 3200 個約束
ι 操作約產生 64 個約束
因此完整的 Keccak-1600 (共 24 輪)將在 Groth 16 中產生 185, 856 個約束。
參考 Ingonyama 的 ICICLE 庫中的數據,在一塊 Nvidia 4090 GPU 上生成一個 Keccak 的 ZK 證明大約需要 30-40 毫秒,在 CPU 上則約為 450 毫秒。如果需要證明 8192 次 Keccak 運算,GPU 至少需要 250 至 300 秒,而 CPU 可能需要接近 一小時。
嘗試二:基於查找表的證明系統(Lookup-based Proof Systems)
一種更現代的優化方案是對數據進行批量處理(例如每 4 位或 8 位一組),並通過查找表來執行所有的位運算。換句話說,將每個 64 位整數切分成若干小塊(例如 8 個 8 位 chunk),再使用查找表完成邏輯操作。
具體包括以下幾種查找表:
異或操作查找表(XOR):一個大小為 2 ⁸ × 2 ⁸ 的查找表,用於計算兩個 8 位 chunk 的異或值。這樣可以用一個約束完成 8 位異或,而不是傳統的 8 個約束。
與操作查找表(AND):同樣是一個 2 ⁸ × 2 ⁸ 的查找表,用於兩個 8 位 chunk 的按位與操作,節省約束的效果與 XOR 類似。
左旋操作查找表(Rotate-left):為了處理 Keccak 中頻繁出現的 rotate-left 操作,引入了多個查找表。具體為:七個大小為 2 ⁸ 的查找表,分別對應旋轉距離為 8 k+ 1、 8 k+ 2 等(其中 k 為非負整數)。相較於嘗試一(Attempt 1)完全不處理旋轉操作,這種方式會引入額外開銷——每輪大約增加 192 個約束。不過與其他部分相比,這個開銷仍然相對較小。
為了實現這種系統,我們不再使用 Groth 16 ,而是更適合採用 Stwo、Plonky 3 等小域證明系統,這類系統對查找表支持更加完善。在該方案下,每次完整的 Keccak 運算大約需要 27, 264 個約束,並結合查找表的調用,可大幅減少整體約束數,相較 Groth 16 顯著優化。
然而,這種優化在性能上並非絕對佔優。因為查找表本身的調用和管理也會帶來開銷,若處理不當,可能抵消約束數量減少所帶來的優勢。因此,其實際運行效率在某些場景下可能不如基於 Groth 16 的實現。
嘗試三:Binius
鑑於查找表(lookup)或定製門電路(customized gates)所帶來的加速在實際中可能不及預期,原因在於查找本身的開銷可能抵消其帶來的約束優化效果,因此我們需探索其他路徑來進一步提升 Keccak 的證明效率。
這正是 Keccak 被譽為“零知識聖盃”的原因所在。與之相比,早期的哈希函數如 SHA-256 和 Blake 2/3 ,雖也依賴於異或(XOR)、與(AND)等位運算,但其最大性能瓶頸源於整數加法。而整數加法在證明系統中通常通過將其拆解為多個 4-bit 塊來優化,從而大幅提升性能。但 Keccak 並不涉及任何整數加法,因此這些優化策略在此處失效。
目前最前沿的解決方案是 Binius。該系統的核心思想是:既然 Keccak 完全由位運算組成,我們便可以使用以 位為基本單位 的證明系統來實現。這便是 Binius 的突破之處。
在 Binius 中,Keccak 被表示為在有限域 𝐹₂(即二元域)上的運算。由於 XOR 本質上就是 𝐹₂ 中的加法,因此其相關開銷幾乎完全消除。整體過程被構造為一系列多項式運算,位旋轉操作也可在按位處理模型中輕鬆實現。證明成本主要集中於 χ 步中出現的 AND 門。
Binius 的基準測試顯示,其在證明 8192 次 Keccak 運算時,僅需約 12.35 秒,遠優於 Groth 16 (嘗試一)和查找表方法(嘗試二)。
Binius 是終點嗎?其實並非如此。我們發現通過去除 Keccak 證明中的某些冗餘部分,還有可能進一步提升約五倍的性能,超過當前的 Binius 實現。
Polyhedra 推出 Binary GKR:專為 Keccak 優化的二進制證明系統
Polyhedra 團隊正在構建全新的證明系統 —— Binary GKR(詳見:ePrint 2025/717 ),這是一個專門針對 二進制操作高效證明 的框架,特別適用於像 Keccak 這樣以位運算為核心的函數。Binary GKR 的核心優勢來自以下三項關鍵技術創新:
1. 基於 GKR 協議,優化重複計算
我們在 Binary GKR 的設計中選擇以 GKR 協議(Goldwasser–Kalai–Rothblum) 為基礎,原因在於它能夠有效降低處理重複性計算所帶來的冗餘開銷。
在典型的 zkEVM 場景中,Keccak 往往以 "外掛證明器(sidecar prover)" 的角色出現,用於批量處理 zkEVM 所委託的大量 Keccak 運算任務。因此,我們面向的電路結構天然具有大量的重複模式,例如: 8192 次 Keccak 調用 是一種常見規模。
更重要的是,Keccak 算法本身就極具重複性:
它在 5 × 5 的狀態矩陣上反覆執行相似的布爾操作;
整個過程包含 24 輪幾乎一致的步驟;
各輪之間結構相同,僅輸入狀態不同。
這樣的特性,使得 Keccak 成為 GKR 協議的“天然適配對象”:
Verifier 成本較低,適合高頻驗證場景;
Prover 可充分利用結構重複性,重用計算路徑,大幅簡化證明開銷;
相比傳統通用證明系統,在批量 Keccak 場景中具備顯著性能優勢。
2. 基於二進制域的多項式承諾
我們採用了一種基於線性碼的多項式承諾方案,該方案直接在二進制域上運行。正如我們此前提到的,使用原生的二進制表示,使我們能夠“免費”獲得諸如異或(XOR)這樣的操作。此外,與 Binius 的方法類似,基於二進制域的多項式承諾避免了使用更大數域所帶來的冗餘,這使系統在性能和效率上都得到了顯著提升。
3. 用於二進制操作的預計算表
Binary GKR 論文中的關鍵創新在於:通過充分利用電路結構的高稀疏性,顯著提升了 GKR 協議的證明效率。即使在同時處理多個比特的情況下,這種稀疏性依然得以保留。們的做法是將多個比特“打包”進 GKR 協議中的多項式中(注意:這些是中間多項式,無需進行承諾),然後直接在這些打包的數據上執行 GKR 協議的運算。
由於稀疏性仍然很高,我們可以利用預計算表,讓證明者以遠低於傳統 GKR 協議的計算開銷來生成證明。這一優化顯著提升了 GKR 在處理二進制關係時的效率。
本文將重點介紹上述第三項技術優化:用於二進制操作的預計算表。
將比特打包進多項式
我們方案的核心是一種專為數據並行布爾電路設計的 GKR 協議求和檢驗(sumcheck)新方法。該方法通過將多個比特打包進多項式中,有效減少了證明者的計算負擔,顯著提升了效率。

更高效地評估二進制關係
相較於傳統 GKR,Binary GKR 帶來了全新的優化空間。


該預處理表非常小。通過合理設置參數,我們可以將表的大小控制在約 15 MB。該大小可輕鬆放入 CPU 的 L3 緩存中,使得查表操作非常高效。
這一技術幾乎適用於所有二進制操作,是 Binary GKR 構造中性能提升的核心所在。
實現與評估
我們基於 Rust 的 arkworks 生態系統實現了 SNARK 系統,並在不同規模的隨機布爾電路上進行了全面的基準測試。
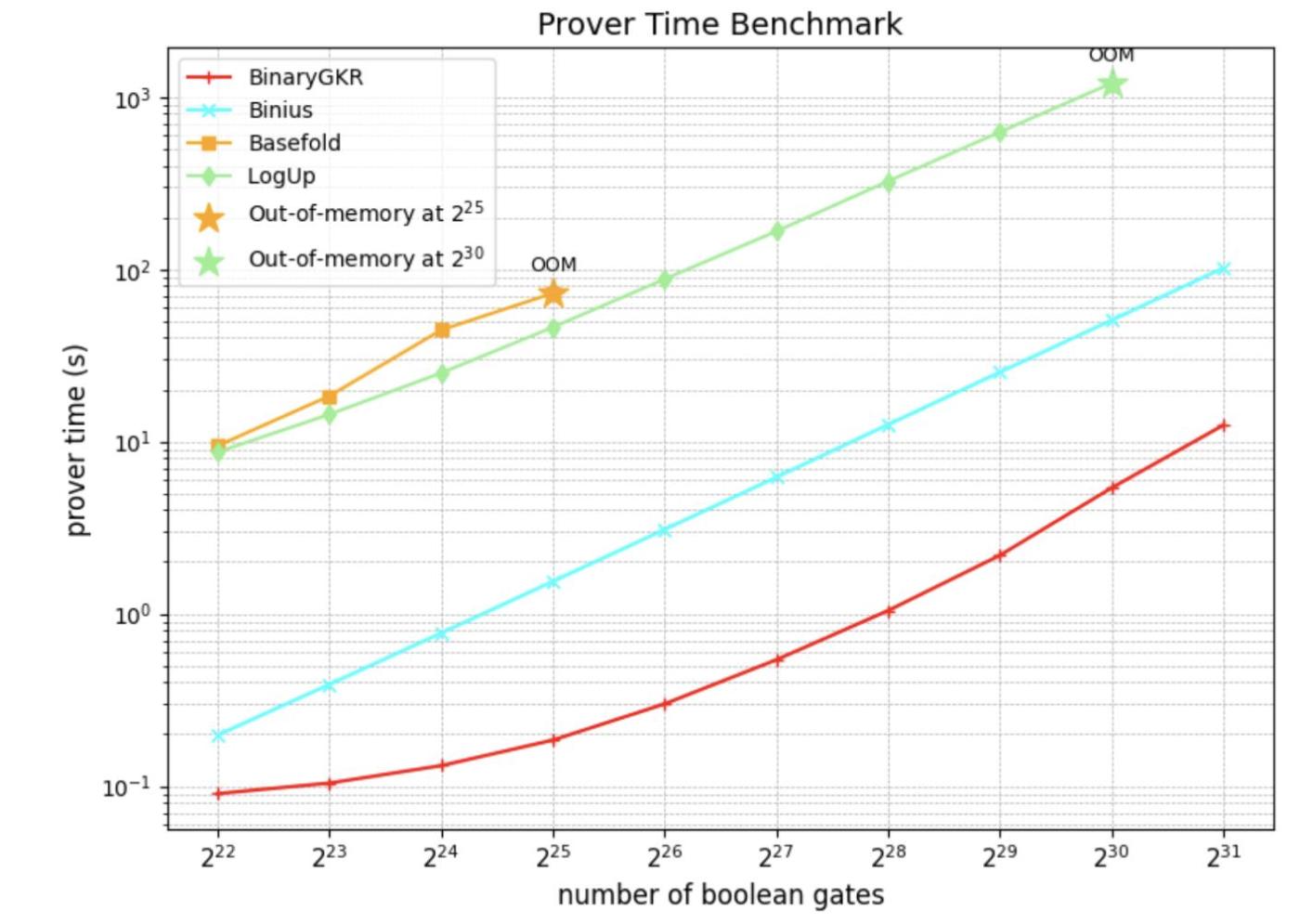
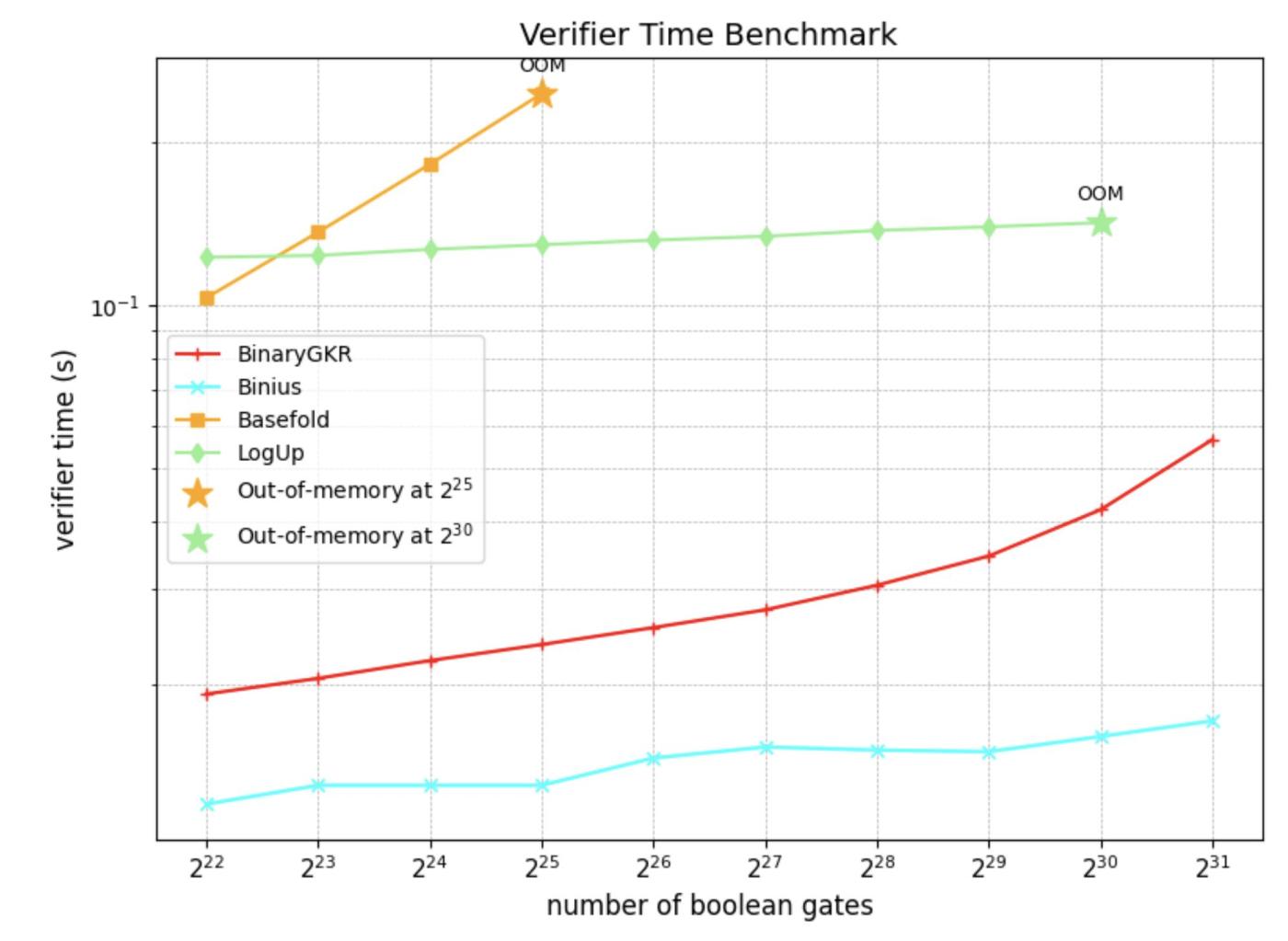
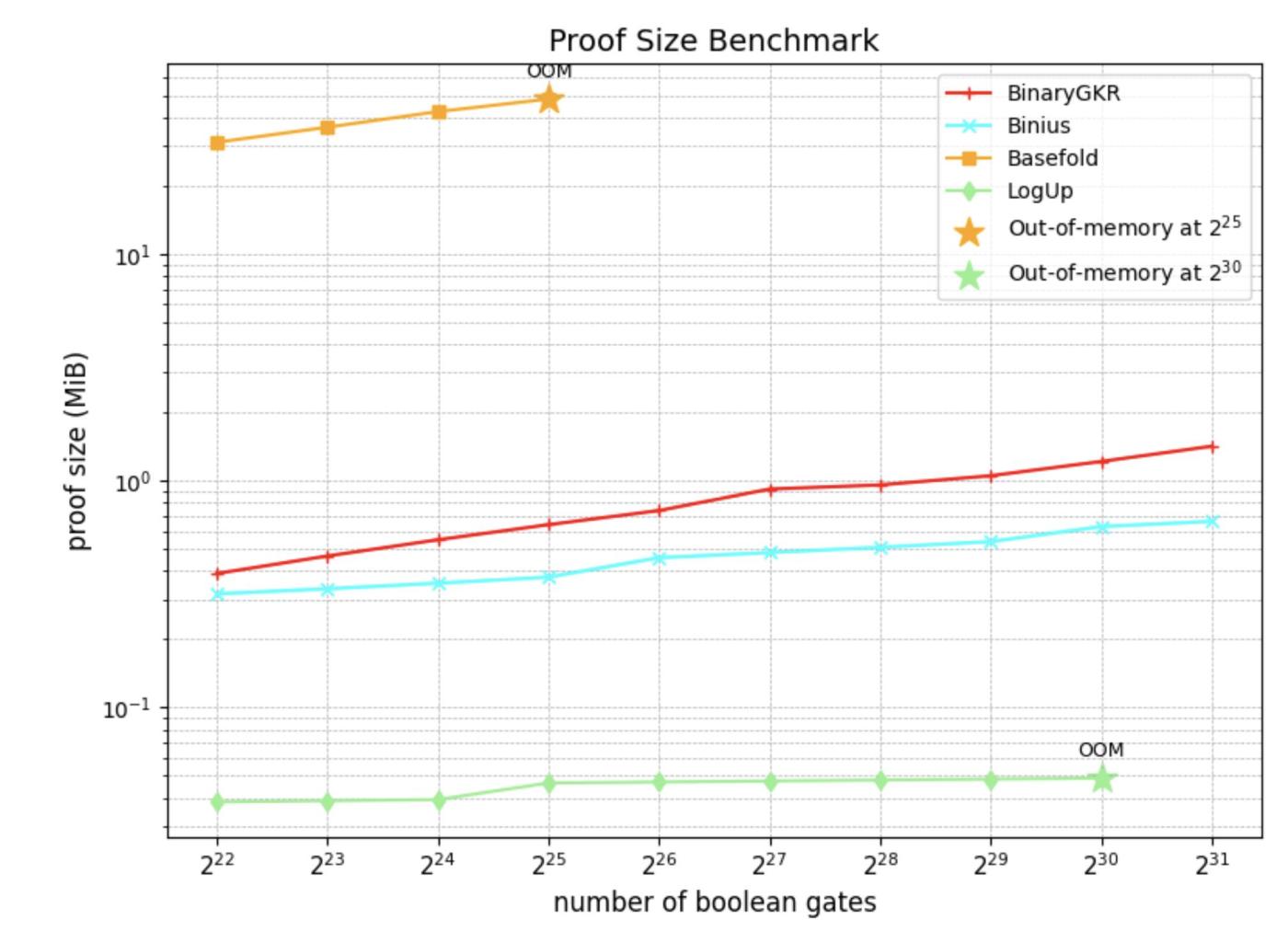
除了隨機布爾電路,我們還聚焦於零知識證明的“聖盃”——Keccak。我們將所提出的方法與 Binius 在 Keccak 證明上的表現進行了對比。兩者均基於二進制域操作。
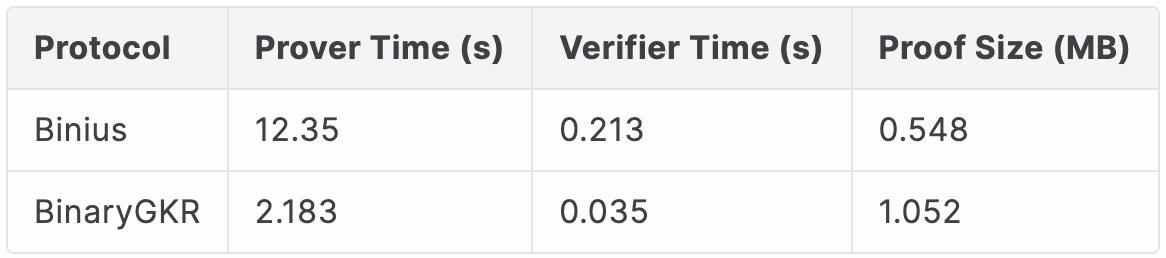
在處理 8192 次 Keccak 調用時,Binius 生成證明耗時 12.35 秒,而我們的方法僅需 2.18 秒。同時,得益於 Keccak 的結構簡潔,我們的驗證時間也更短,僅為 0.035 秒。通信開銷方面,我們的證明大小為 1.052 MB。
結語
本文介紹了 Polyhedra 團隊在零知識證明領域的最新進展,重點在於針對二進制函數(如 Keccak)的優化。這一成果可作為各類 zkEVM 構建的高效“輔助模塊”。
我們計劃將 Binary GKR 集成至 RISC Zero、SP 1 等 zkEVM 系統中,進一步驗證其在緩解 Keccak 性能瓶頸方面的作用。最終目標,是在不破壞現有 EVM 架構的前提下,加速以太坊向 layer-1 全面 SNARK 化邁進。
原文鏈接:https://blog.polyhedra.network/binary-gkr/