關於激勵匿名參與

05-27

本文為機器翻譯

展示原文

關於激勵匿名參與

upload_0bca3fb7f6b0d2fc3fe0596f28531112 1300×867 189 KB

\cdot ⋅
簡而言之，區塊鏈活動通過參與共享協議的獨立參與者來促進。激勵這種參與是一個關鍵的設計考慮因素，尤其是在無需許可、對抗和匿名的環境中。我們在第 1 節中提出了一個模型並激勵參與博弈。在第 2 節中，我們分析了該博弈的對稱匿名均衡。然後，我們將該框架應用於兩種環境。第 3 節詳細介紹了證明者市場，旨在激勵至少一個證明的生成。第 4 節轉向工作量證明協議，旨在激勵至少 50% 的參與（旨在避免 51% 攻擊）。在這兩種情況下，我們都推導出協議的最佳激勵結構，以最小化其成本。我們在第 5 節中總結如何擴展該模型以及用於引導參與的其他特定於區塊鏈的技術。
\cdot ⋅
作者： maryam & mike – 2025 年 5 月 26 日。
\cdot ⋅
感謝Akilesh 、 Noam 、 Matt和Barnabé對這篇文章的審閱和討論！

內容

（1）動機與模型
 （1.1）參與博弈模型
 (1.2). 一個簡單的、非匿名的解決方案
 (1.3). 非對稱均衡
 （2）彩票支付規則的對稱均衡
 (2.1). 考慮較大的n n
（3）證明者市場成本最小化
 （3.1）針對至少一個參與者進行優化
 （3.2）。漸近線
 （3.3） 1 + \ln c 1 + ln c邊界很緊
 （4）工作量證明目標函數
 （4.1）。漸近線
 （5）結論與未來工作
 (5.1). 替代成本函數
 （5.2）異構主體與信息不對稱
 （5.3）代幣、空投和區塊鏈應用

1. 動機與模型

開場片段——你在附近的體育酒吧，有一張桌子準備觀看NBA季後賽。你不想一個人看，所以打算讓群聊裡的人知道你也在。為了讓大家更有可能來，你主動提出買第一輪雞翅，但你首先需要決定點多少。如果你點的太少，可能會沒人來，因為他們會擔心其他人會去，導致雞翅不夠吃。如果你點的太多，即使大家都來了，桌子上也坐不下了。那麼，為了保證你的朋友能來，而不是所有朋友都來，最佳的雞翅數量是多少呢？ ¹

這個故事在區塊鏈協議設計中經常出現。協議希望以某種形式吸引參與，並使用激勵措施來引導參與：

工作量證明提供區塊獎勵來激勵礦工解決加密難題。
權益證明為區塊上的質押和正確投票提供共識獎勵。
證明者市場協調計算密集型的 ZK 證明的生產。

至關重要的是，區塊鏈還希望允許無需許可的參與。這使得協調問題更加困難。本文提出了一個激勵參與的模型，並分析了匿名、共同價值支付規則的對稱均衡。具體來說，我們研究了每個參與者都以概率p採取購買彩票的混合策略時的均衡。

1.1.參與博弈模型

我們對參與博弈進行如下建模：

玩家——玩家是一個戰略代理，可以根據機制選擇購買入場券。
參與者——參與者是購買入場券的玩家。
協議——該協議是一個具有成本函數（或等效地，積極的估值函數）的代理，用於誘導參與。
付款規則——協議實現的功能，將參與者集合映射到各自的付款。

假設參與博弈中有n名玩家。每位玩家面臨相同的入場費q ，因此這是一個共同價值拍賣。為簡單起見，在本文的其餘部分我們使用q= 1 。每位參與者都可以確定性地決定是否加入；他們也可以選擇採用隨機策略，以一定的概率p加入。在決定是否加入之前，參與者需要遵守協議指定的支付規則。支付規則可能取決於已實現的參與者集合，並且可以隨機化。每位參與者選擇一個行動來最大化他們的預期效用，即他們收到的預期付款減去入場費（如果他們選擇參與）。

以下兩節介紹匿名性和對稱性的概念。

1.2. 一個簡單的非匿名解決方案

假設該協議旨在吸引至少一名參與者，並假設玩家通過決勝局來決定是否參與。一個簡單的機制如下：“選擇一位特定的玩家，記為WINNER ，並告訴他們，如果他們參與，你將支付他們 1 美元。” 這個簡單的解決方案具有許多理想的性質：

每個人的個體理性（因為每個參與者不參與都會獲得零效用），並且
令人滿意的參與均衡（ WINNER將參與，並且沒有其他人會參與），並且
協議的支付最小化（因為 1 美元是門票費，因此是獲得參與者的最小成本）。

如果協議設計者願意選擇獲勝者，那麼這個解決方案就足夠了。2 我們不會就此止步，而是專注於^一組匿名的解決方案。

定義（非正式）：匿名支付規則不能依賴於玩家的身份。

我們在第 3.3 節中形式化地闡述了這一屬性，但希望它直觀易懂。這些支付規則必須平等對待每位玩家。規則可以取決於玩家的行為（例如，將獎金平均分配給所有參賽者），也可以隨機化（例如，將獎金隨機分配給單個參賽者）。然而，上述機制依賴於玩家的身份，並非匿名。

1.3. 非對稱均衡

另外，考慮以下場景：“一位玩家，記為COMMITTER ，公開承諾購買門票併成為參與者。”根據支付規則，此承諾可能會抑制其他玩家參與。例如，假設支付規則將 1 美元的獎金平均分配給所有參與者。在這種情況下，第二個考慮加入的玩家必然會產生負效用，因為他支付 1 美元卻獲得 1/2 美元。這導致沒有其他人加入協議，而COMMITTER獲得全部獎金。這種均衡最小化了協議的支付，但要求參與者選擇COMMITTER ，從而將協調的複雜性轉嫁給玩家。我們以此例為動機，將注意力限制在對稱均衡上。

定義：在對稱均衡中，每個玩家使用相同的策略。

該策略可以是確定性的（例如，總是買票並參與），也可以是混合性的（例如，以概率p p買票）。由於這些確定性策略可以分別被認為是p=0 p = 0或p=1 p = 1 ，因此任何對稱均衡都可以由單個值p\in[0,1] p ∈ [ 0 , 1 ]完全指定。在這樣的均衡中，參與者的數量取自\text{Binomial}(n,p) Binomial ( n , p ) ，其中n n是參與者的數量。

2.彩票支付規則的對稱均衡

由於我們的注意力僅限於對稱均衡，因此參與者的策略只有三種結果：

沒有人加入（ p=0 p = 0 ），
每個人都加入（ p=1 p = 1 ），
每個人加入的概率為p\in (0,1) p ∈ ( 0 , 1 ) 。

根據支付規則，以上任何一種結果都有可能出現。本節研究彩票支付規則。

定義：彩票支付規則通過從參與者集合中均勻隨機地選擇一名獲勝者來向單個玩家支付金額為x x的獎金。

彩票支付規則是匿名的，並根據x x的大小引入對稱均衡p p 。協議設定x x的值，玩家決定是否加入，獎金全額髮放給其中一名參與者。如果x<1 x < 1 ，則屬於情況 (1)；沒有人會加入，因為獎金低於報名費。如果x\geq n x ≥ n ，則屬於情況 (2)；每個人都會參加，因為保證（預期）他們獲得的報酬高於報名費。對於x x的其他值，參與者數量將是從\text{Binomial}(n,p) Binomial ( n , p )中抽取的隨機變量，其中p\in (0,1) p ∈ ( 0 , 1 ) 。協議可以通過調整x x來移動平均值np n p 。

我們可以刻畫上述 (3) 情形下的對稱均衡，其中每個參與者混合各自的策略並以概率p p加入。（對此有很多方法；我們在此使用微分法展示一種明確的方法；另一種方法參見附註# 1 。）我們考慮參與者i i的決策，將其他參與者的策略固定為p p 。i i選擇其加入概率p' p ′以最大化其預期效用，

\begin{align}U_i(p') &= \bigg[ \underbrace{\mathbb{E}\left[\frac{x}{1+Y}\right]}_{\text{預期獎金}} - \underbrace{1}_{\text{票價}}\bigg] p', \; \text{where } Y \sim \text{二項式}(n-1,p) \\&= \left[x\cdot \frac{1-(1-p)^n}{np} -1\right]p'\end{align}

Ui ( p ′ ) = [ E [ x 1 + Y ]     預期獎金− 1   票價] p ′ ,其中Y ∼二項式( n − 1 , p ) = [ x ⋅ 1 − ( 1 − p ) n n p − 1 ] p ′

換句話說，如果玩家i i加入並在參與者中贏得彩票，她將獲得x x的獎勵。具體而言，由於其他n-1 n − 1 位玩家均以概率p p獨立加入，因此除i i之外的參與者人數將從\text{Binomial}(n-1,p) Binomial ( n − 1 , p )中抽取。i i加入的效用等於獎勵金額減去彩票價格。i i加入的效用（概率p' p ′）等於她加入的效用乘以p' p ′ ，因為i i不加入的效用為 0。

對於對稱策略p p ，要達到均衡， p'=p p ′ = p必須在所有p'\in[0,1] p ′ ∈ [ 0 , 1 ]中最大化該表達式。一階條件為

\begin{align}\frac{\partial U_i}{\partial p'} = x\cdot \frac{1-(1-p)^n}{np} -1.\end{align}

[數學處理錯誤]

將其設置為零，我們得到x x和p p之間關係的解析解，

x\cdot \frac{1-(1-p)^n}{np} -1 = 0\implies \boxed{x = \frac{np}{1-(1-p)^n}}

x ⋅ 1 − ( 1 − p ) n n p − 1 = 0 ⟹ x = np1− ( 1 − p ) n

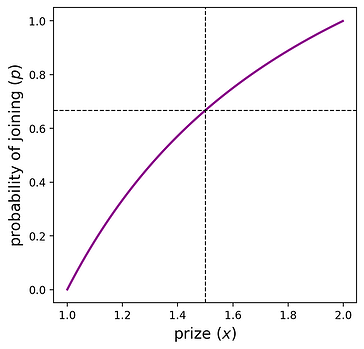
這告訴我們：“給定一個大小為x x的獎勵，多少概率p p會達到對稱均衡”或者等效地，“如果協議設計者希望參與者數量來自\text{Binomial}(n,p) Binomial ( n , p ) ，他們會設置一個大小為x x的獎勵。” 下圖顯示了當n = 2時這些變量之間的關係。

upload_d625b6de301ed0283341dc168f71222a 931×895 37.7 KB

虛線的解釋是：“如果協議設定獎金x=1.5 ，則策略p=2 / 3是對稱均衡。” 另外，請注意，如果獎金<1 < 1或>2 > 2 ，則參與者加入的概率分別為 0 或 1。這些就是本節開頭描述的“無人加入”和“所有人都加入”的結果。對於內部區域x \in (1,2) x ∈ ( 1 , 2 ) ，每個x x都會誘導一個唯一的p p 。

附言#1推導同一方程的另一種方法是考慮所有玩家集合的總現金流。對於給定的p p ，玩家集合預期支付np n p的入場費。因此，協議需要支付np n p的預期補償（因為這是一個競爭均衡，任何超額價值都將被競爭抵消）。當協議選擇一個獎勵x x時，只要至少有一個玩家參與，玩家集合就會獲得該獎勵。這種情況發生的概率為1-(1-p)^n 1 − ( 1 − p ) n ，這意味著玩家集合獲得x \cdot (1-(1-p)^n) x ⋅ ( 1 − ( 1 − p ) n )的獎勵。

題外話#2：混合策略均衡的一個有趣特性是，玩家對任何行動都漠不關心（這也是他們一開始就隨機化行為的原因）。在上面的例子中，如果其他所有人都以概率p加入，那麼玩家i從任何行動中獲得的效用為零。你可以通過將x代入她的效用函數來說明這一點，
\begin{align}U_i(p') &= \bigg[ x \cdot \frac{1-(1-p)^n}{np} -1\bigg] \cdot p' \\&= \bigg[\frac{np}{1-(1-p)^n}\cdot \frac{1-(1-p)^n}{np} -1\bigg] p' \\&= (1-1)p'\\&= 0.\end{align}
[數學處理錯誤]
另一種解釋是，均衡是完全競爭的。這導致結果與由此產生的混合策略之間無差異。

2.1 考慮較大的n n

回憶這段關係

x = \frac{np}{1-(1-p)^n}。

x = np1− ( 1 − p ) n 。

關於這個方程的一個有趣的觀察是，對於較大的n n ，我們可以將x x重寫為\mu=np μ = n p （預期參與者人數）的函數，對於較小的x x使用(1-x) \rightarrow e^{-x} ( 1 − x ) → e − x ，如下所示

x(\mu) \approx \frac{\mu}{1-e^{-\mu}}。

x ( μ ) ≈ μ 1 − e − μ 。

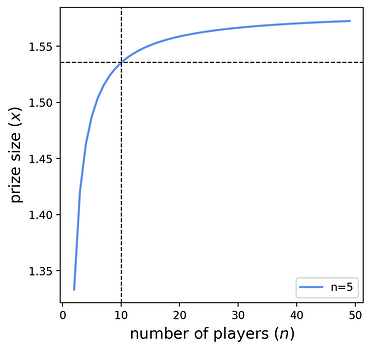
協議可以使用這個簡單的公式來確定期望的平均參與人數\mu μ ，而無需知道n n 。例如，如果協議希望預期只有一個參與者，則應設置1/(1-1/e)\approx 1.582 1 / ( 1 − 1 / e ) ≈ 1.582的獎金。也就是說，協議支付高於1 1入場費58 \ % 的溢價，以吸引預期一名參與者。隨著n n 的增長，這個近似值會提高。下圖顯示了平均吸引一名參與者所需的協議獎金。它還顯示了當n \to \infty n → ∞趨近於x(1)=1/(1-1/e) x ( 1 ) = 1 / ( 1 − 1 / e ) 時的極限。

upload_9cde4a87098e4108fb332832c204d531 949×895 33.3 KB

虛線可以解釋為：“如果n=10 ，那麼協議設計者需要設置至少x=1.535的獎勵，才能預期吸引一名參與者。” 當然，協議設計者也可以選擇更高的獎勵，以降低無人參與的風險。下一節將正式描述這種權衡。

3. 驗證者市場成本最小化

到目前為止，我們已經展示了協議如何通過改變x x來實現特定的預期參與人數\mu μ 。現在，我們來考慮那些特別厭惡低參與度的協議。我們通過引入“低參與度懲罰”來形式化這一點。在本節中，我們首先考察證明者市場。在第 4 節中，我們將探討由工作量證明共識機制引發的另一種低參與度懲罰機制。

我們設想一個 ZK Rollup，它希望激勵生成成本高昂的證明。市場設計者可能只關心至少有 1 位^證明者參與（並支付入場費，即生成證明的成本）。3 進一步假設，如果完全沒有參與，協議可以自行生成證明，成本為c （你可以將 c視為“外部選項”）。這樣，我們可以將低參與度懲罰寫成參與者數量k的函數，如下所示

\begin{align}\text{低參與懲罰}(k) =\begin{cases}c & \text{if } k = 0 \\0 &\text{otherwise}.\end{cases}\end{align}

[數學處理錯誤]

自然，協議設計者希望選擇最小化其總成本（獎金數額加上任何罰款）的支付規則。

3.1. 針對至少一名參與者進行優化

上述分析允許協議設計者在x x和p p之間關係所導致的對稱均衡下，選擇獎勵的幅度，以達到一定程度的參與。在低參與懲罰下，協議的成本函數（我們將其表示為C_p C p ）為

C_p = c \cdot \Pr[\text{不參與}] + x \cdot \Pr[\text{參與}].

C p = c ⋅ Pr [不參與] + x ⋅ Pr [參與] 。

協議力求最小化這一成本，並且在給定c c 的情況下選擇x x時，協議面臨著權衡。x x的值過低，協議很可能會遭受c c 的懲罰； x x的值過高，則協議的成本會直接增加，因為協議必須支付更大的獎勵。基於對稱均衡中每個參與者參與概率p p的事實，我們可以得出：

C_p = c \cdot (1-p)^n + x \cdot (1-(1-p)^n)。

Cp = c⋅ （ 1 − p ） n + x⋅ （ 1− （ 1 − p ） n ）。

其中x = \frac{np}{1-(1-p)^n} x = n p 1 − ( 1 − p ) n （我們上面推導的關係），這簡化為

C_p = c \cdot (1-p)^n + np。

Cp = c⋅ （ 1 − p ） n + np 。

這就是協議成本，它試圖在p \in [0,1] p ∈ [ 0 , 1 ]上最小化它。利用最優概率p^* p ∗ ，協議可以直接計算出在p^* p ∗處達到對稱均衡所需的獎勵大小。我們使用一階條件最小化協議成本，

\begin{align}\frac{\partial C_p}{\partial p} &= -cn(1-p)^{n-1} + n =0 \\&\implies p^* = 1-c^{-\frac{1}{n-1}}\end{align}

[數學處理錯誤]

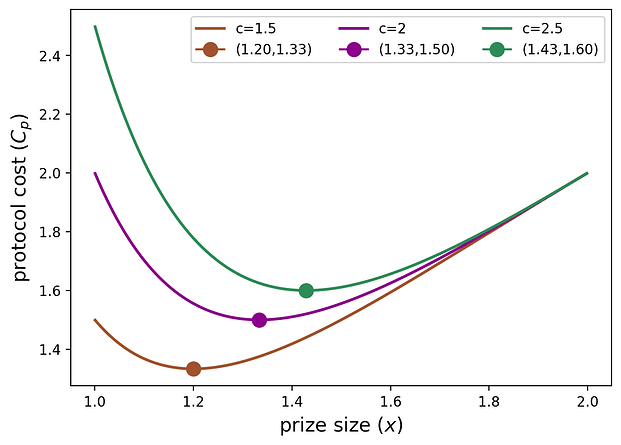
二階導數在p \in [0,1] p ∈ [ 0 , 1 ]上始終為負，因此p^* p ∗確實是協議成本的唯一局部最小值。下圖顯示了協議成本作為x x的函數（它與p\in(0,1) p ∈ ( 0 , 1 )存在雙射），其中n = 2和c=1.5,2,2.5 c = 1.5 , 2 , 2.5分別成立。

upload_68cf7e34e09faa5dfee6d7ce96b8e0fb 1246×895 62.3 KB

x^* x ∗ 的值（在圖中以點表示）在c c中不斷增加，因為協議面臨更高的不參與懲罰，因此它選擇更高的x^* x ∗ （這會導致更高的p^* p ∗ ），以確保至少有一名玩家參與。根據p^* p ∗ ，我們以閉式計算出最優獎勵額：

\begin{align}x^* &= \frac{np^*}{1-(1-p^*)^n} \\&= \frac{n(1-c^{-1/(n-1)})}{1-c^{-n/(n-1)}}\end{align}

[數學處理錯誤]

我們還計算了最佳協議成本

\begin{align}C_p^* &= c \cdot (1-p^*)^n + np^* \\&= n-(n-1) c^{-1/(n-1)}\end{align}

[數學處理錯誤]

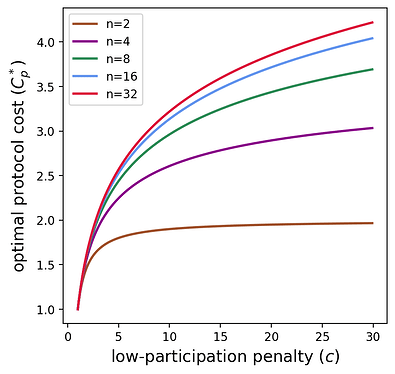
下圖有助於將該成本可視化為n, c的函數。

upload_32974a3ccb2b0fc03b6c63af46b5baa4 945×895 66.1 KB

我們發現，隨著低參與度懲罰的增加，協議成本似乎呈對數增長。下一節將通過觀察協議成本的漸近行為來形式化這種關係。

3.2 漸近線

一個自然而然的問題是，p^*、x^*、C_p^* p ∗ 、 x ∗ 、 C ∗ p的值如何作為c c的函數進行縮放。具體來說，協議設計者可能想知道，假設遊戲中有大量玩家n ，它們的效用如何作為c c的函數進行縮放。展開（推導見腳註⁴ ），我們得到

\begin{align}p^* &= \frac{\ln c}{n-1} + O\left(\frac{(\ln c)^2}{n^2}\right).\end{align}

[數學處理錯誤]

類似地，我們可以檢查x^* x ∗的漸近行為（推導見腳註⁵ ），這是成本最小化協議的最佳獎勵：

\begin{align}x^* = \frac{\ln c}{1 - 1/c} + O\left(\frac{(\ln c)^2}{n}\right).\end{align}

[數學處理錯誤]

最後，我們考察協議支付的最優成本C_p^* C ∗ p的漸近行為（推導見腳註⁶ ）：

\begin{align}C_p^* &=1 + \ln c + O\left(\frac{(\ln c)^2}{n}\right).\end{align}

[數學處理錯誤]

至關重要的是，我們看到，當n\to\infty n → ∞時，協議的總成本按1+ \ln c 1 + ln進行縮放c 。這對於協議來說非常棒，因為它提供了成本與外部選項函數的對數界限。此外，最優成本與n無關。這在無需許可的環境中非常實用，因為協議可以僅根據外部選項的質量（即低參與度懲罰）來設定最優獎勵，而無需知道有多少玩家！這也意味著即使遊戲中的玩家數量非常龐大，協議也可以確保他們的成本是有限的^。7

下一節將回答這個問題：“我們能突破這個對數界限嗎？”更正式地說，是否存在一個匿名支付規則，使得由此產生的對稱均衡具有協議成本C_p < 1+\ln c C p < 1 + ln c ？下一節我們會證明答案是否定的！協議成本嚴格受限於1+\ln c 1 + ln角

3.3 1+\ln c 1 + ln c邊界很緊

Note for the math/formalism-averse crowd: this section can be safely skipped!

我們知道在對稱均衡中每個參與者加入的概率為p p 。我們需要將1.2 節中概述的匿名屬性形式化，以便將我們的機制與其他匿名支付規則進行比較。支付規則\pi(S,r) π ( S , r )將加入的參與者集合S\subseteq [n] S ⊆ [ n ]和隨機種子r r作為輸入，並向每個參與者輸出支付。如果S S非空，上一節中的機制將以概率1/|S| 1 / | S |向隨機參與者支付彩票獎金x x ，否則不支付任何人。如果機制\pi(S,r) π ( S , r )相對於代理人的行為逐點對稱，我們稱其為（事後）匿名的。形式上，如果對於所有r r和S S以及所有排列\ sigma σ ， \pi(S,r)=\pi(\sigma(S),r) π ( S , r ) = π ( σ ( S ) , r ) ，則\ pi π是事後匿名的。當一個機制是匿名的時，我們可以將其支付規則重寫為\pi(S,r)=\pi(k,r) π ( S , r ) = π ( k , r ) ，其中k=|S| k = | S | ，並且取自\text{Binom}(n,p) Binom ( n , p ) 。現在我們只關心參與者的數量，而不是特定的集合。

設\pi(k,r) π ( k , r )為一個具有對稱均衡p p的匿名機制。那麼，拍賣商的預期成本為

C_p = \underbrace{c \cdot (1-p)^n}_{\text{無參與}} + \underbrace{\mathbb{E}_{k,r}[\pi(k,r)]}_{\text{參與}}。

C p = c ⋅ ( 1 − p ) n     無參與+ E k , r [ π ( k , r ) ]    參與。

這個期望值代入隨機性實現r r和每個可能的參與者數量k k 。在期望值中，我們知道k k 個參與者中的每一個都必須是理性的才能參與抽獎。總的來說，任何協議的期望值都必須至少支付每個參與者的入場費。形式上， \mathbb{E}_{k,r}[\pi(k,r)] \geq np. E k , r [ π ( k , r ) ] ≥ n p 。代入這個期望值，我們再次得到如下形式：

C_p \geq c \cdot (1-p)^n + np。

Cp≥c⋅ （ 1 − p ） n + np 。

在等式成立的情況下，這正是彩票機制的協議成本。因此，它具有相同的最優協議成本C_p^* = n-(n-1) c^{-1/(n-1)} C ∗ p = n − ( n − 1 ) c − 1 / ( n − 1 )和漸近行為1+\ln c 1 + ln c當n \to \infty n → ∞時適用。在匿名和個體理性機制中，抽籤機制在最小化“至少一名玩家”目標方面是最優的！

4. 工作量證明目標函數

在上一節中，僅當沒有參與時，協議才會產生成本c c ，對應於參與者數量k k的階躍函數，

\begin{align}\text{低參與懲罰}(k) =\begin{cases}c & \text{if } k = 0 \\0 &\text{otherwise}.\end{cases}\end{align}

低參與懲罰（ k ） = { c如果k = 0 0否則。

這個成本函數對於證明者市場的例子來說是合理的，因為在這個例子中，單個參與者是必要的，因為只需一個證明就能滿足協議的要求。在其他區塊鏈環境中，不同的低參與懲罰（或一般參與評估函數）