作者:Yiming Ma, Yao Zeng, and Anthony Lee Zhang,來源:The University of Chicago,編譯:錢家彥
一、引言
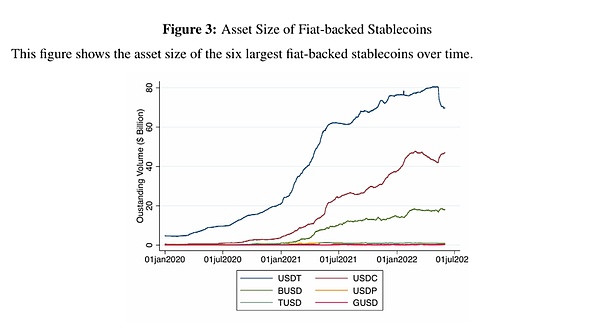
法幣支持的穩定幣是區塊鏈資產,其價值宣稱穩定在1美元。這種價格穩定性是通過承諾以至少1美元的美元計價資產(如銀行存款、國債、公司債券和貸款)來支持每一枚穩定幣代幣實現的。六大美元支持的穩定幣的市值已從2020年初的56億美元增長到2022年初的超過1300億美元。穩定幣有可能成為一種廣泛接受的支付手段,與法幣和銀行存款競爭,這引發了關於如何減輕對金融穩定的潛在風險以及最優監管框架應是什麼的積極討論。
理想的穩定幣始終以穩定的1美元進行交易,且不會出現恐慌性擠兌。然而,穩定幣持有非流動性資產,卻承諾1美元的固定贖回價值。與貨幣市場基金(MMF)或商業銀行不同,這種1美元的贖回僅限於特定的機構套利者。絕大多數投資者只能在二級市場交易所交易穩定幣,這與投資者在二級市場交易ETF份額類似。這些投資者按照二級市場價格進行交易,該價格經常因市場的供需壓力而在1美元上下波動。由於穩定幣價格是在均衡狀態下確定的,那麼穩定幣投資者何時以及為何會想要擠兌呢? 穩定幣的價格偏差與其擠兌風險有何關聯?
本文通過構建一個穩定幣市場結構的框架來回答這些問題,展示發行方、套利者和客戶如何相互作用,以確定穩定幣價格的穩定性和恐慌性擠兌的可能性。本文研究結果為穩定幣的最優監管提供了重要見解。這些見解尤為相關,因為不同司法管轄區最近提出了不同的穩定幣監管方案,且這些方案並不總是相互一致。
首先,一些提案要求穩定幣發行人向所有投資者提供無限制的直接贖回,這實際上消除了當前的兩層市場結構。此類政策確實會通過更具競爭力的套利促進價格穩定。然而,在穩定幣被允許繼續進行流動性轉換的情況下,我們的模型表明,更高效的套利也會放大恐慌性擠兌的風險。相比之下,對套利者徵收贖回費用會通過限制套利來降低擠兌風險,但會以犧牲價格穩定為代價。
其次,許多政策提案對穩定幣發行人儲備資產的安全性和流動性施加了限制。我們的研究結果表明,儲備資產政策應與管理贖回的政策相協調,因為這些因素共同決定了價格穩定和擠兌風險這兩個結果。
第三,允許支付股息進一步提高了穩定幣的價格穩定性,並可能降低擠兌風險。綜上所述,雖然價格穩定和低擠兌風險都是穩定幣的理想特徵,但它們本質上是不同的,並且對政策干預的反應也不同。
二、穩定幣詳述
穩定幣是區塊鏈資產,其價值宣稱穩定在1美元。區塊鏈資產可以實現自我託管:用戶可以使用諸如MetaMask之類的加密錢包軟件直接持有、發送和接收穩定幣。這些穩定幣不存放在任何受信任的中介機構中:相反,“私鑰”(一種通常僅保存在用戶硬件設備上的長數字代碼)被用來向區塊鏈網絡證明用戶擁有其穩定幣,並指示網絡採取諸如將穩定幣轉移到其他錢包等行動。其他人無法訪問個人的私鑰,因此他們無法從個人錢包中取走資金。
與比特幣等其他區塊鏈資產相比,穩定幣的顯著特徵是相對價格穩定。最大的穩定幣發行方試圖通過承諾以至少1美元的鏈下美元資產支持每一枚穩定幣代幣來實現價格穩定。這些法幣支持的穩定幣在過去幾年中經歷了快速擴張。在兩年內,六大法幣偏向型穩定幣的總資產規模從2020年初的56億美元增長到2022年初超過1300億美元(圖3)。最大的兩種穩定幣是泰達幣(USDT)和Circle美元硬幣(USDC),在2022年1月,它們的總市值達到764億美元,佔總市場規模的50%以上。幣安美元(BUSD)、Paxos(PUSD)、TrueUSD(TUSD)和Gemini美元(GUSD)的規模則小得多。
在本節的其餘部分,本文概述穩定幣的用途和穩定幣市場結構。
2.1 穩定幣的用途
穩定幣是一種成本相當低的交易和持有美元資產的方式。如果A國的匯款人向B國的收款人匯款,她可以在加密貨幣交易所用A國的法定貨幣購買穩定幣,將這些穩定幣提取到自己的加密貨幣錢包,然後發送到B國收款人的錢包。收款人隨後可以將這些資金存入本國的加密貨幣交易所,將穩定幣兌換成法定貨幣,然後提取法定貨幣。將穩定幣從一個加密貨幣錢包發送到另一個加密貨幣錢包相對快速且成本較低。截至2023年1月,在以太坊區塊鏈上發送穩定幣的交易在一分鐘內即可完成,每筆交易成本約為1美元,與發送的穩定幣數量無關。穩定幣還可以用作價值儲存手段; 它們可以免費無限期地存放在加密錢包中。
因此,雖然在發達國家,穩定幣的使用成本高於運作良好的銀行服務,但在傳統金融基礎設施運作不佳的情況下,它們具有競爭力。例如,在交易必須跨越國界、資本管制和金融抑制普遍存在、通貨膨脹率高或對金融中介機構信任度低的環境中,穩定幣正得到廣泛應用。
穩定幣還用於與其他區塊鏈智能合約進行交易。例如,市場參與者可以使用穩定幣代幣,通過Uniswap等自動化做市商協議購買其他區塊鏈代幣,如ETH、MKR或UNI。市場參與者還可以在Aave和Maker等借貸協議上借出穩定幣代幣,從而獲得正利率,也可以將這些資產用作抵押品來借入其他資產。從某種程度上說,穩定幣為區塊鏈生態系統提供了安全的價值儲存手段和交換媒介。
2.2 市場結構
穩定幣代幣在一級市場以美元現金的形式被創建(“鑄造”)或贖回(“銷燬”),如圖4左側所示。要創建穩定幣代幣,套利者向發行方發送1美元,然後發行方將一個穩定幣代幣發送到市場參與者的加密錢包中。類似地,要贖回穩定幣代幣,市場參與者每向發行方的加密錢包發送一個穩定幣代幣,發行方就會通過銀行轉賬等方式向市場參與者的銀行賬戶發送1美元。穩定幣的一級市場類似於傳統金融體系中的貨幣市場基金。
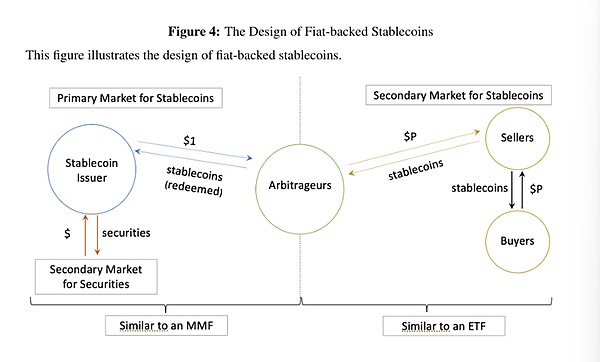
大多數市場參與者無法成為套利者來贖回和創建穩定幣代幣,而且穩定幣發行方在市場參與者進入一級市場的難易程度和成本方面存在差異。據市場參與者稱,USDC允許一般企業註冊成為套利者,而USDT則需要漫長的盡職調查過程,並對套利者的註冊地加以限制。此外,USDT規定最低交易規模為10萬美元,每次贖回收取0.1%和1000美元中的較大值作為費用。
大多數市場參與者在二級市場上將現有的穩定幣兌換成法定貨幣。加密貨幣交易所允許投資者存入美元,然後與其他市場參與者進行美元與穩定幣的交易。因此,二級市場上穩定幣代幣的價格由供求關係決定。當穩定幣拋售激增時,二級市場價格下跌,但不會直接導致儲備資產清算。通過這種方式,二級市場上穩定幣的買賣類似於競爭易所中ETF份額的交易。
然而,二級市場的拋售壓力可能會通過套利者蔓延到一級市場。當二級市場價格跌破1美元時,套利者可以通過在二級市場購買穩定幣代幣,並在一級市場與穩定幣發行方以1:1的比例兌換1美元來獲利。通過這種套利,一級市場穩定幣1美元的贖回價值會將二級市場穩定幣的交易價格拉向1美元。與此同時,這一套利過程還意味著,當穩定幣發行方清算儲備以滿足套利者的現金贖回時,二級市場投資者的拋售壓力最終會引發儲備資產的出售。如果非流動性儲備資產被折價出售,這些甩賣的成本可能會特別高。
三、數據
在本節中,我們將解釋我們的主要數據來源。
一級市場數據:
本文分析中使用的核心數據集是以太坊、雪崩和波場區塊鏈上六種最大的法幣支持穩定幣(USDT、USDC、USDP、TUSD和GUSD)的每次穩定幣創建和贖回事件的數據。我們從每個區塊鏈的“鏈瀏覽器”網站獲取這些數據,這些網站將交易級區塊鏈數據處理成可用格式。本文使用Etherscan處理以太坊數據,Snowtrace處理雪崩數據,Tronscan處理波場數據。通過數據提取過程,可以看到每次穩定幣創建和贖回事件的精確時間戳、贖回或創建的穩定幣數量,以及參與穩定幣創建和贖回的實體的錢包地址。區塊鏈只記錄錢包地址,同一機構可能有多個錢包地址。在數據採集過程中,本文將Etherscan標籤明確表明屬於同一機構的錢包合併。然而,這個過程可能並不詳盡,因此本文所計算的套利集中度應被視為真實套利集中度的下限。
二級市場數據:
對於每種穩定幣,本文從包括幣安(Binance)、Bitfinex、Bitstamp、Bittrex、Gemini、Kraken、Coinbase、Alterdice、Bequant和Cexio在內的幾家大型交易所提取直接美元對穩定幣交易的每小時收盤價。主要交易所之間穩定幣價格的差異通常可以忽略不計,因此價格序列不會受到我們對不同交易所賦予的權重的實質性影響。本文對二級市場價格進行1%水平的縮尾處理。
四、穩定幣的其他事實
在本節中,本文將介紹一組關於穩定幣的新事實,以為模型和校準提供依據。
4.1 二級市場價格
事實1:穩定幣在二級市場的交易價格通常會偏離1美元。
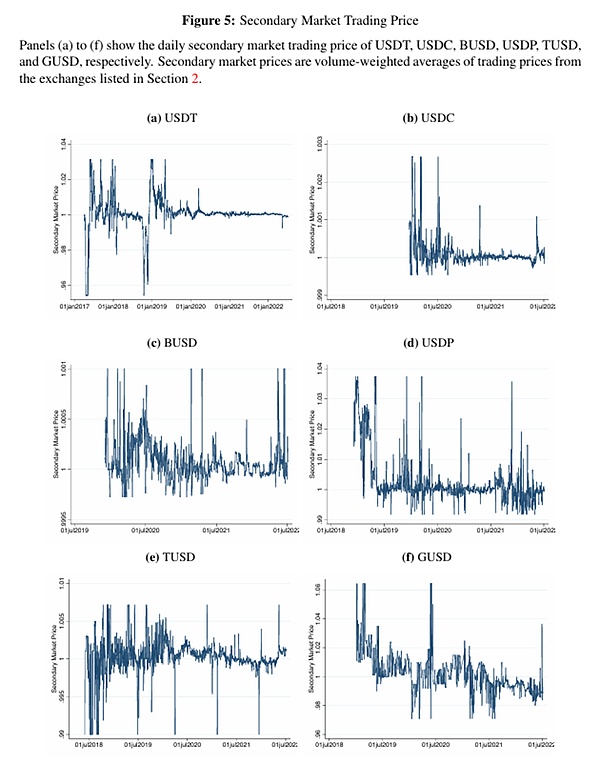
圖5展示了不同穩定幣在二級市場上隨時間的交易價格。本文觀察到,二級市場價格很少固定在1美元。相反,在穩定幣樣本中,穩定幣27.2%至41.6%的時間以折價交易,57.3%至72.8%的時間以溢價交易(見表1a)。這些價格偏差的程度因穩定幣而異。雖然USDT的平均折價為54個基點,但USDC的平均折價僅為1個基點。BUSD、TUSD和USDP的平均折價也低於USDT,而GUSD的平均折價最高。中位數折價的幅度通常小於平均折價,但橫截面的差異仍然相似。例如,USDT的中位數折價為11個基點,而USDC的中位數折價小於1個基點。當考慮一個共同的樣本期時,幅度也會減小。
從2020年1月開始,當時所有六種穩定幣都有交易,但各幣種之間的差異仍然存在,USDT的平均折價幅度大於USDC(見表1b)。平均溢價和中位數溢價在橫截面中也顯示出顯著差異。

4.2 一級市場集中度
事實2:穩定幣在一級市場的贖回和創造由一小部分套利者執行,其集中程度因穩定幣而異。
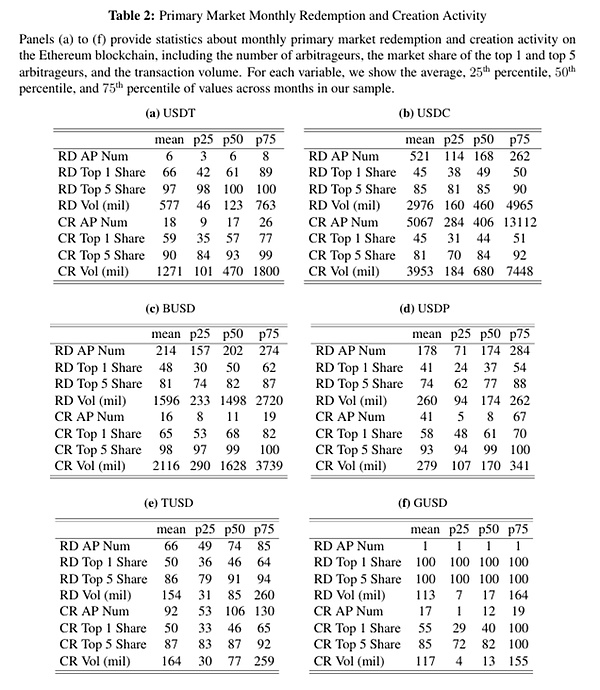
表2展示了以太坊區塊鏈上不同穩定幣的月度一級市場贖回和創建活動的特徵。平均每月,USDT只有6名套利者參與贖回,而USDC有521名。套利者的市場份額集中度普遍較高,但仍因穩定幣而異。USDT最大的套利者完成了所有贖回活動的66%,而USDC最大的套利者完成了45%。相比之下,大多數其他穩定幣在套利者數量和套利者集中度方面介於USDT和USDC之間。在交易量方面,平均每月USDT的贖回量為5.77億美元,而USDC為29.76億美元。相比之下,USDT的未償代幣總量是USDC的1.5至2倍。因此,USDC套利者數量較多且集中度較低,也與相對於總資產規模而言較高的贖回量相關。創建量較大,參與創建的套利者相對較多,但不同穩定幣之間的趨勢和套利集中度仍然相似。
4.3 二級市場價格與一級市場集中度
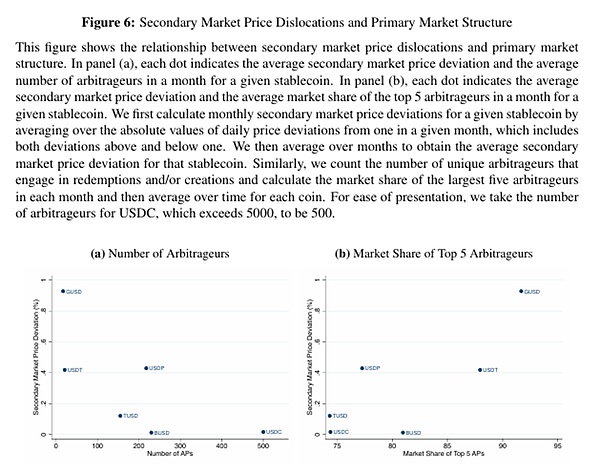
事實3:套利者群體更為集中的穩定幣在二級市場上會出現更為明顯的價格偏離。
接下來分析價格偏差與套利者集中度之間的關係。對於給定的穩定幣,通過對給定月份內每日價格相對於1的偏差絕對值求平均值來計算月度二級市場價格偏差,其中包括高於和低於1的偏差。然後我們對各月數據求平均值,以得到該穩定幣的平均價格偏差。同樣,統計參與贖回和/或鑄造的獨特套利者數量,並計算每個月最大的五個套利者的市場份額以及每種穩定幣隨時間的平均值。
結果如圖6a所示。一個明顯的負趨勢出現了:與套利者較多的穩定幣(如USDC)相比,套利者較少的穩定幣(如USDT)在二級市場價格上相對於1的平均偏差更高。另一種衡量套利者集中度的方法是通過最大套利者的市場份額。在圖6b中,我們用前五大套利者的市場份額重複了分析。這種關係是正相關的。前五大套利者在總贖回和鑄造中始終佔據較大份額的穩定幣,其平均價格偏差高於套利者集中度較低的其他穩定幣。換句話說,似乎更高的套利競爭與二級市場價格錯位的減少有關。
4.4 流動性轉換
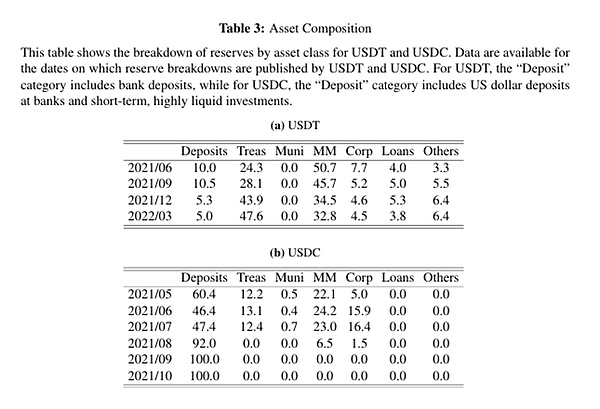
事實4:穩定幣通過投資非流動資產進行不同程度的流動性轉換。
穩定幣發行方持有不同程度非流動性的以美元計價的資產作為儲備。表3顯示了報告日USDT和USDC儲備資產的構成。總體而言,USDT和USDC的儲備資產都並非完全具有流動性,其中USDT的儲備資產非流動性更強。
五、理論框架
5.1穩定幣擠兌與套利的中心化
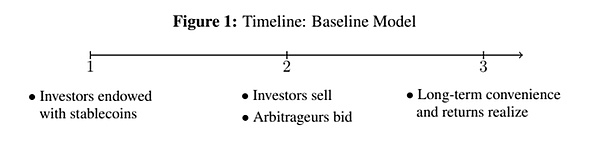
基準經濟模型基於戴蒙德和迪布維格(1983)的研究構建,有三個時間點,t = 1、2、3,且不存在時間貼現。本文在圖1中提供了一個時間線來說明該經濟模型:
有兩組風險中性參與者:
1)由i索引的穩定幣投資者競爭群體,以及
2)n個穩定幣套利者組成的群體。
有兩類資產:
1)美元,它無風險、流動性強,用作計價單位;
2)一種非流動性且可能具有生產性的儲備資產。
投資者共同持有在t = 1時最初由儲備資產支持的穩定幣。儲備資產的初始價值被標準化為1美元。在t = 2和t = 3時,投資者需決定是在t = 2時提前清算其穩定幣(這可能引發擠兌),還是持有至t = 3到期以獲取長期收益(我們將在下文詳述)。與銀行儲戶不同,穩定幣投資者無法直接從發行人處贖回其持有的穩定幣。相反,他們會在t = 2時,按照傑克林(1987年)以及法裡、戈洛索夫和齊文斯基(2009年)提出的機制,在二級市場將穩定幣出售給套利者,然後由套利者從發行人處贖回現金。與這些模型一樣,投資者通過獨立提交市價訂單來出售穩定幣。這一假設與實證證據相符,該證據表明散戶投資者更傾向於使用市價訂單,尤其是在價差較窄時(凱利和泰特洛克,2013年),穩定幣的情況便是如此。本文用λ表示以市場價格p2出售穩定幣的投資者比例。
套利者在考慮他們預期能夠從發行方贖回的金額後,在雙重拍賣中進行競爭性投標,以確定投資者出售λ穩定幣的價格p2。在基準模型中,假設套利者不能持有淨庫存,因此他們在t = 2時在一級市場上的淨贖回量必須與他們在二級市場上的購買量相等。在附錄C.1中,我們表明這一假設與絕大多數套利者持有的穩定幣數量非常少這一實證觀察結果是一致的。套利者面臨二次庫存成本:套利者j承擔成本,用於從二級市場向一級市場套利zj單位的穩定幣,其中χ可以被視為衡量套利者的資產負債表容量:當χ較高時,庫存成本較低。
在決定是否提前清算其穩定幣時,投資者在t = 2時收到關於t = 3時經濟基本面的私人信息。遵循全局博弈文獻,每個投資者i在t = 2時獲得一個私人信號θi = θ + εi,其中噪聲項εi在[−ε,ε]上獨立且均勻分佈。本文關注任意小的噪聲,即ε→ 0,但模型結果在極限情況之外也成立。
基本面θ反映了總體風險水平,並決定了穩定幣在t = 3時的長期價值。以1 - π(θ)的概率,經濟進入不良狀態:儲備資產失敗,投資者既不會獲得任何名義回報,也不會從持有由無價值資產支持的穩定幣中獲得任何長期收益。以π(θ)的概率,經濟進入良好狀態:儲備資產產生R(ϕ) ≥ 1美元的正值,歸發行人所有。穩定幣繼續運營,剩餘的1 - λ投資者每枚穩定幣獲得長期收益η > 0,每單位剩餘儲備資產獲得初始價值1。這種長期收益η可以由投資者借出穩定幣的回報來解釋。
根據逆向歸納法,首先考慮 p2,即投資者提前清算穩定幣時所獲得的價格。在正文中,我們推導了由套利者競爭性出價產生的逆需求函數。如果套利者進行策略性出價,本文模型類似於克萊姆佩雷爾和邁耶(1989)的設定,該設定存在多個均衡。然而,在選擇最接近標準線性解的均衡出價曲線的均衡選擇規則下,本文關於套利能力影響穩定幣價格的核心經濟見解保持不變。
本文通過令價格等於邊際成本來推導逆需求函數。
假設 λ ≤ 1−ϕ,這意味著發行人具有償債能力,那麼在二級市場以價格 p2 購買 zj 單位並在一級市場贖回的套利者將獲得:

在任何對稱均衡中,每個套利者吸收的總庫存為z∗ j = λ n。如果發行人將價格視為給定的,為了使z∗ j成為吸收的最優數量,價格必須等於在z∗ j處吸收額外穩定幣數量的邊際價值。也就是說,對(5.1)關於zj求導,令其等於0,然後求解p2得到:
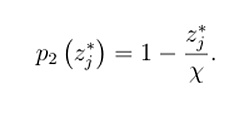
用文字表述,價格就是邊際贖回價值1減去邊際庫存成本z∗ j χ。在對稱均衡中代入z∗ j = λ n得到
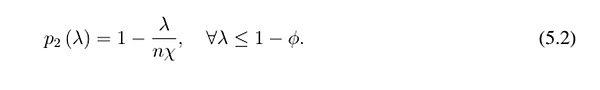
在資不抵債的情況下,λ > 1 - ϕ,穩定幣的每一單位只能按其清算價值(1 - ϕ)/λ贖回。由於投資者提交的是市價訂單,贖回價值不取決於套利者的數量選擇。因此,套利者的利潤被修正為
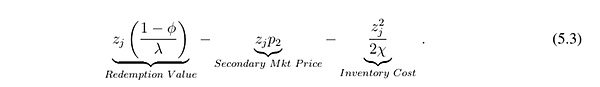
同樣,在對稱均衡中,價格必須等於套利者吸收額外數量的邊際價值。對 (5.3) 關於 zj 求導,令其等於 0,並代入 zj∗ = λn,得到
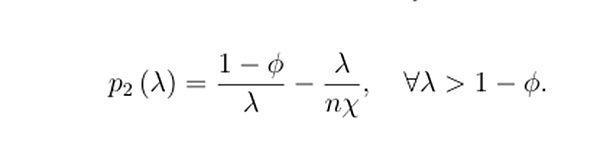
與(5.2)的唯一區別在於,贖回價值被修改為 (1−ϕ)/ λ。本文將這些結果總結在以下引理中。
引理1.穩定幣在t = 2時的二級市場價格由下式給出:
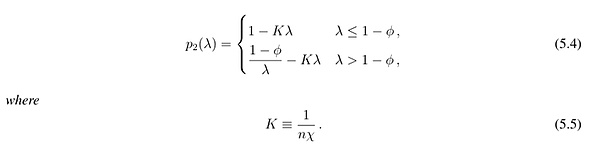
引理1表明,對於任何總贖回量λ > 0,p2隨K的增加而減小,隨χ和n的增加而增大。直觀地說,當套利者的資本狀況更好(χ更高)且數量更多(n更高)時,二級市場價格受投資者拋售的影響較小。我們將K稱為套利能力,它在分析中起著核心作用,因為它衡量了發行人保持償付能力時二級市場需求的斜率。套利者的出價為穩定幣創造了一條向下傾斜的需求曲線,當n或χ增加時,斜率變得更陡,從而降低了穩定幣拋售的價格影響。
還需注意,p2在任何地方都嚴格隨λ遞減:投資者拋售得越多,價格就越低。這一點很重要,因為它在投資者的拋售決策中產生了策略替代性:當許多其他投資者都在拋售時,某個投資者預期拋售所得會減少,從而抑制其拋售行為。這種力量與經典銀行擠兌模型(如Diamond和Dybvig,1983)中的策略互補性形成對比,在經典銀行擠兌模型中,儲戶取款可獲得固定的存款價值。
接下來,本文研究了t=3時的情況。
全局博弈框架能夠針對任何基本參數值求解唯一均衡。理論上,可以得到:
命題1 :存在一個唯一的閾值均衡,在該均衡中,如果投資者獲得的信號低於閾值θ∗,則出售穩定幣,否則不出售。
命題1表明,具有投資者私人且有噪聲信號的模型存在唯一的閾值均衡。投資者的清算決策由其信號唯一確定:當且僅當其信號低於某個閾值時,才會在t = 2時出售穩定幣。換句話說,當信號處於閾值時,在出售和持有之間無差異。鑑於存在唯一的擠兌閾值,我們可以證明,無差異條件意味著以下拉普拉斯方程:
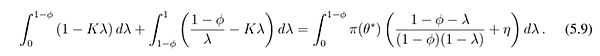
求解拉普拉斯方程可得出運行閾值的解析解,並呈現出關於穩定幣擠兌風險的直觀比較靜態分析:
命題2:運行閾值由下式給出:
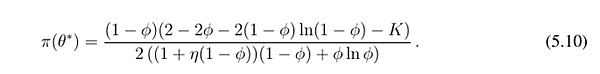
i). 運行閾值,即運行風險,隨K的增大而減小(即隨n的增大而增大,隨χ的增大而增大)。
ii). 擠兌閾值,即擠兌風險,當且僅當在 ϕ 中增加時
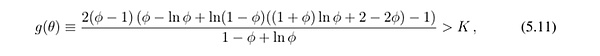
其中g(ϕ)在ϕ上連續且嚴格遞減,並且滿足limϕ→0 g(ϕ) > 0。
一個核心理論結果是命題2的第一部分,它表明更有效的套利,即K值更小,會加劇擠兌風險。
命題2的第二部分表明,當g(ϕ) > K時,穩定幣流動性轉換水平越高,擠兌風險就越高。對於給定的K,當ϕ足夠小時,這一條件成立。直觀地說,當穩定幣持有更多非流動性儲備資產時,投資者之間的先發優勢會增加,因為選擇不出售的投資者將不得不非自願地承擔由出售投資者引發的更高清算成本。
5.2 價格穩定與最優穩定幣設計
在分析了穩定幣的運行風險及其與套利集中的關係後,我們通過納入t = 1時穩定幣的價格穩定性以及t = 0時交易前博弈中發行人的最優設計選擇,對基準模型進行了擴展。
具體推理過程詳見原文, 關於穩定幣發行人對套利者集中度的最優選擇,得出以下結果:
命題3:假設G是線性的,且ϕ足夠小使得(5.11)式成立,那麼發行人對K的最優選擇隨ϕ遞減:如果儲備資產的流動性更差,那麼發行人會最優地選擇一個更集中的套利部門。
命題3源於價格穩定與金融穩定之間的權衡。穩定幣發行方選擇套利集中度K,以權衡降低擠兌風險帶來的收益與降低價格穩定性產生的成本。當資產非流動性ϕ較高時,擠兌風險增加。此時,發行方應更願意犧牲價格穩定性來限制擠兌風險,從而導致K的最優值更高。
六、政策影響
多個司法管轄區對穩定幣的最優監管給予了更多關注。監管機構和市場參與者希望穩定幣既具有低擠兌風險,又能保持價格穩定。本文框架強調,這兩個理想目標彼此不同,由不同的經濟力量驅動。特別是,我們強調了價格穩定和金融穩定之間的權衡,並表明一些政策可能以犧牲一個目標為代價來實現另一個目標。在本節中,本文運用模型預測來闡明擬議的穩定幣贖回、儲備和利息支付監管對價格穩定和金融穩定意味著什麼。
經過一系列分析,本文發現股息發行可能還有其他影響。例如,股息發行可能會加劇穩定幣發行商之間的價格競爭,這可能會鼓勵新進入者並提高配置效率。根據美國證券法,發放股息的穩定幣也可能被歸類為證券,並面臨監管風險。我們將對這些和其他因素的分析留待未來研究。
七、結論
本文分析了穩定幣擠兌風險與價格穩定之間的權衡。從宏觀層面來看,穩定幣擠兌源於流動性轉換。穩定幣發行方持有非流動性資產,同時向套利者提供在一級市場以固定1美元贖回穩定幣的選擇權。這種流動性錯配從一級市場蔓延開來,即使有交易所交易,也會引發二級市場投資者擠兌的可能性。
重要的是,穩定幣擠兌風險受套利者部門的市場結構調節,該部門在二級市場和一級市場之間起到 “防火牆” 的作用。當套利者部門效率更高時,二級市場的衝擊會更有效地傳導至一級市場。穩定幣的價格穩定性因此得到改善,但賣家的先發優勢也更高,從而增加了擠兌風險。如果套利者部門效率較低,二級市場的衝擊傳導效果就會較差。價格穩定性會受到影響,但擠兌風險會降低,因為二級市場中穩定幣交易的價格影響會抑制市場參與者的恐慌性拋售。
本文研究結果具有重要的政策意義。儘管監管機構和市場參與者都希望穩定幣既具有較低的擠兌風險,又能保持價格穩定,但這兩個理想目標彼此不同,且由不同的經濟力量驅動。特別是,允許無限制贖回會提高套利效率,這雖然有助於改善價格穩定性,但可能會以更高的擠兌風險為代價。在討論穩定幣是否應允許以股息形式向投資者分配收益時,也必須考慮股息發放對擠兌風險的抑制作用。總體而言,在設計監管措施時,同時考慮價格穩定性和擠兌風險,對於穩定幣行業未來的良好運行和安全至關重要。








