以太坊的 WHIR

08-18

本文為機器翻譯

展示原文

感謝Justin Drake和Tom Wambsgans的深刻且建設性的反饋。

簡介：為什麼以及如何在未來將 WHIR 用於以太坊？

隨著以太坊的持續擴容，對 SNARK 證明系統的要求也日益嚴格：證明必須精簡，驗證必須快如閃電，並且整個系統必須保持簡潔和穩健，以便在極簡硬件上進行驗證——理想情況下，就像 Justin Drake 最近在Ethproofs 大會第二輪電話會議中所建議的那樣，像 Raspberry Pi Pico 2 這樣性能受限的設備。在此背景下，一個應用脫穎而出，成為下一代 SNARK 的試驗場：以太坊即將推出的精益鏈的簽名聚合。它滿足了所有約束條件——高吞吐量、嚴格的延遲、最低的驗證成本、後量子設定——並將作為本文的運行示例。

這些需求正在推動證明系統的一種更廣泛的趨勢：證明系統中從單變量多項式表示向多線性多項式表示的轉變。然而，在多線性環境中工作需要新的工具——尤其是在鄰近度測試方面，像FRI（快速 Reed-Solomon 交互式預言鄰近度證明）這樣的協議不再適用。這就是WHIR 的用武之地。WHIR 是一種用於受約束 Reed-Solomon 碼的遞歸、基於哈希的鄰近度測試協議。它旨在在單變量和多線性模式下高效運行，使其足夠靈活，適用於各種證明系統。WHIR 的核心結合了兩個優雅的理念：一種遞歸摺疊機制（受 STIR 啟發），可以逐輪壓縮域；以及一種輕量級的基於和校驗的約束檢查（類似於 BaseFold），可以最小的開銷確保代數正確性。

最終成果是一個體現簡潔性（以太坊的關鍵特性）的工具，它提供小型證明（通常小於 100 KB，128 位安全位，推測 Reed Solomon 碼具有最大容量的相互關聯一致性）、快速驗證（通常在一毫秒到幾毫秒內，具體取決於所選的哈希函數）和低內存佔用，所有這些都僅依賴於基於哈希的加密假設。WHIR 支持緊湊、低 gas 的 SNARK 驗證，實現高效的簽名聚合，併為在驗證器簡單性至關重要的系統中實現遞歸證明鋪平了道路。

在本文的其餘部分，我們將闡述 WHIR 的工作原理、它的重要性以及它如何幫助塑造以太坊上高效證明系統的未來。

關於現代 SNARK 的一些背景

現代 SNARK 通常通過在多項式交互式預言機證明 (PIOP) 之上疊加多項式承諾方案 (PCS) 來構建。一個常見的例子是 AIR（代數中間表示）模型，其中證明者通過將表的每一列編碼為單變量多項式來提交執行軌跡。這種策略雖然簡單，但卻帶來了可擴展性瓶頸：每一列都成為一個單獨的多項式，導致證明規模龐大且驗證成本高昂——當涉及數百列時，通常需要耗費數兆字節（MB）的驗證成本。

為了克服這個問題，最近的證明系統正在從單變量表示轉向多線性表示。不再對每一列分別進行提交，而是將整個見證編碼為單個多線性多項式。這種變化帶來了諸多優勢：更好的壓縮效果、更簡單的約束表達式，以及取決於軌跡總面積而非形狀的證明大小。Binius、 Jolt和SP1 Hypercube等系統都順應了這一趨勢——其中 SP1 率先使用多線性承諾實現了以太坊區塊的實時證明。

可以使用和校驗協議來完成這種多線性設置中的約束驗證，而不是構造和評估商多項式。和校驗提供了更好的模塊化並可以與多線性編碼無縫協作，儘管在使用小字段時會帶來性能上的權衡。這個限制最近已通過“單變量跳過”優化得到解決，它通過在第一輪中將多個變量完全摺疊在基字段內來加速和校驗。通過在廉價的基字段域中預先做更多的工作，單變量跳過減少了後續輪次中昂貴的擴展字段評估，從而顯著提高了證明器的速度而不會犧牲健全性。除了這種方法之外，人們還在探索其他加速和校驗協議的方法。最近一個值得注意的研究途徑是由S. Bagad 及其合著者提出的。

在這個新的堆棧中，WHIR 起著至關重要的作用：它執行接近度測試步驟，驗證提交的多線性函數確實接近有效的代碼字。

WHIR 如何工作？

本節將以直觀而嚴謹的方式解釋 WHIR 的運作方式，重點介紹其核心機制，而無需深入探討完整的形式化證明。旨在為工程師提供清晰易懂的理解。

Reed–Solomon 碼接近度測試

從高層次上講，WHIR 是一種工具，用於驗證函數f : \mathcal{L} \to \mathbb{F} f : L → F是否“接近”低次多項式，以及該多項式是否滿足某些代數約束。

什麼是裡德-所羅門碼？

Reed-Solomon 碼是通過在有限域上求低次多項式而得到的函數集。更準確地說，假設我們選擇一個有限域\mathbb{F} F和一個子集\mathcal{L} \subseteq \mathbb{F} L ⊆ F ，我們稱之為求值域。一個d次Reed-Solomon 碼為：

\mathrm{RS}[\mathcal{L}, d] = \left\{ f : \mathcal{L} \to \mathbb{F} \ \middle|\ f(x) = \hat{f}(x)\ \text{其中某些多項式 } \hat{f} \text{且 } \deg(\hat{f}) < d \right\}。

RS [ L , d ] = { f : L → F ∣ ∣ f （ x ） = ^ f （ x ）對於某個多項式^ f ，其度數為（ ^ f ） < d } 。

換句話說，這些只是域\mathcal{L} L上所有可能的次數小於d的多項式的求值表。當我們說函數f f “符合碼”時，是指它與這樣的多項式一致。當f f “接近”碼時，是指它與\mathcal{L } L中大多數點上的某個碼字一致——這稱為接近度。

我們為什麼要關心接近度測試？

在證明系統中，證明者可能會向驗證者發送一個函數f ，該函數看起來像是在求一個低次多項式的解，但實際上可能並非如此。為了確保可靠性，驗證者必須檢查f是否接近 Reed-Solomon 碼中的一個真實碼字。這是鄰近度測試的核心。

多線性視圖和平滑代碼

WHIR 使用的是結構更完善的 RS 碼。它不使用任意多項式，而是使用多線性多項式——即每個變量的次數最多為 1 的多項式。例如，對於變量x、y 、 z ，多線性多項式可以表示為3 + 2x + 5y + 7xz ，但不能表示為x ^ 2 x 2或y ^ 2z y 2 z 。

為此，WHIR 假設：

定義域\mathcal{L} L是\mathbb{F}^* F ∗的乘法子群，其大小為 2 的冪，
度數界限d d也是 2 的冪，比如d = 2^m d = 2 m 。

在這些條件下，任何次數小於2^m 2 m的單變量多項式\hat{f} ^ f都可以唯一地視為一個包含m個變量的多線性多項式。在點x \in \mathcal{L} x ∈ L處求原多項式的解，等價於在由x x導出的一個特殊向量處求其新的多線性對應項（我們也稱之為\hat{f} ^ f ）。這給出了以下優雅的重新解釋：

f(x) = \hat{f}(\mathrm{pow}(x, m)), \quad \text{其中 } \mathrm{pow}(x, m) = (x^{2^{0}}, x^{2^{1}}, \dots, x^{2^{m-1}})。

f （ x ） = ^ f （ p o w （ x ， m ）），其中p o w ( x , m ) = ( x 2 0 , x 2 1 , … , x 2 m − 1 ) 。

此變換將簡單單變量域\mathcal{L} L中的每個點映射到m m維布爾超立方體上的一個點。它使我們能夠應用高效的多線性技術（例如和校驗協議），同時保留原始代碼結構的簡潔性。

向代碼添加約束

在許多協議中，我們不僅要檢查f是否接近某個多項式，還要確保該多項式滿足某個代數條件。例如，我們可能希望強制執行以下規則：

\hat{f}(r) = y \quad \text{或更一般地} \quad \sum_{\mathbf{b} \in \{0,1\}^m} \hat{w}(\hat{f}(\mathbf{b}), \mathbf{b}) = \sigma,

^ f ( r ) = y或者更一般地∑ b ∈ { 0 , 1 } m ^ w ( ^ f ( b ) , b ) = σ ,

其中\hat{w} ^ w是固定約束多項式， \sigma σ是已知值。

為了表達這一點，WHIR 使用了 RS 碼的一種變體，稱為約束 Reed-Solomon 碼。正式定義如下：

\mathrm{CRS}[\mathcal{L}, m, \hat{w}, \sigma] := \left\{ f = \hat{f}|_\mathcal{L} \ \middle| \ \sum_{\mathbf{b} \in \{0,1\}^m} \hat{w}(\hat{f}(\mathbf{b}), \mathbf{b}) = \sigma \right\},

C R S [ L ， m ， ^ w ， σ ] ： = ⎧ ⎨ ⎩ f = ^ f | L ∣ ∣∣ ∣ ∑ b ∈ { 0 , 1 } m ^ w ( ^ f ( b ) , b ) = σ ⎫ ⎬ ⎭ ,

其中f f是多線性多項式\hat{f} ^ f在\mathcal{L} L上的求值。

此約束確保f f不僅來自多項式，而且滿足特定代數恆等式。

摺疊問題：遞歸壓縮

為了提高鄰近度測試的效率，WHIR 應用了一種稱為摺疊的遞歸壓縮技術。受 FRI 和STIR等協議的啟發，摺疊技術會逐漸將大問題簡化為更小的等效問題。每一輪都會縮小函數的定義域和複雜度，同時保留其基本屬性，從而使驗證者能夠輕鬆地進行最終檢查。經過足夠多的輪次後，問題會變得非常小，可以直接且低成本地進行檢查。

WHIR 回合：結合摺疊和校驗

此過程中的核心操作是摺疊，最好通過直觀的交錯式 Reed-Solomon 解釋來理解。與其使用複雜的遞歸公式，不如將域\mathcal{L} L想象成被分組為小塊。每個塊中的證明者數據定義了一個小的局部多線性多項式。摺疊整個塊就像在驗證者發出的隨機挑戰\alpha α下評估這個局部多項式一樣簡單。

從數學上講，如果我們讓p_y(X_1, \dots, X_k) p y ( X 1 , ... , X k )成為與新的較小域中的點y y對應的點塊的局部多項式，則摺疊操作就是：

\mathrm{摺疊}_k(f, \alpha)(y) = p_y(\alpha_1, \dots, \alpha_k)

摺疊k ( f , α ) ( y ) = p y ( α 1 , … , α k )

此單一評估使用隨機挑戰向量\alpha \in \mathbb{F}^k α ∈ F k ，優雅地將原始塊中2^k 2 k個點的信息壓縮為新函數的單個值。

WHIR 有力地增強了這一想法。在一輪中，它使用k k維隨機挑戰\alpha α ，通過將其並行應用於兩個進程，一次性消除k k個變量：

k k輪和校驗將主要代數約束簡化為一個新的、更簡單的約束。
摺疊（作為局部評估）將函數本身縮小為更小的函數。

整個輪次將原始鄰近實例轉換為一個明顯較小的新實例，其中約束多項式\hat{w} ^ w和目標\sigma σ均被更新：

f \in \mathrm{CRS}[\mathbb{F}, \mathcal{L}, m, \hat{w}, \sigma] \quad \xrightarrow{\text{一輪 WHIR}} \quad f' \in \mathrm{CRS}[\mathbb{F}, \mathcal{L}^{(2)}, mk, \hat{w}', \sigma']

f ∈ CRS [ F , L , m , ^ w , σ ]一輪 WHIR − −−−−−−−− → f ′ ∈ C R S [ F , L ( 2 ) , m − k , ^ w ′ , σ ′ ]

這帶來了至關重要的效率提升。雖然我們將變量數量減少了k k （將多項式空間縮小了2^k 2 k倍），但求值域僅減少了一半。這顯著提高了代碼速率\rho = 2^m / |\mathcal{L}| ρ = 2 m / | L | 。新的速率\rho' ρ ′計算公式如下：

\rho' = 2^{1-k} \rho

ρ ′ = 2 1 − k ρ

2^{-k} 2 − k項來自於消息空間的縮減（更少的多項式係數），而2^1 2 1項來自於域大小的減半。降低每輪的編碼率是 WHIR 查詢複雜度低的關鍵原因。

摺疊的健全性保證

摺疊過程經過精心設計，堅固耐用，這對於整個證明系統的安全性至關重要。

摺疊保留了函數與代碼的距離。如果函數起始位置距離任何有效代碼字較遠，則摺疊後它仍然保持較遠。錯誤無法通過代數混合來隱藏或抵消。
在列表解碼設置中，多個有效碼字可能接近證明者的函數。摺疊操作保證（以高概率）將整個鄰近碼字列表忠實地映射到新的、更小的問題上。遞歸過程中不會引入任何偽解或錯誤解，從而確保驗證者不會被誤導。

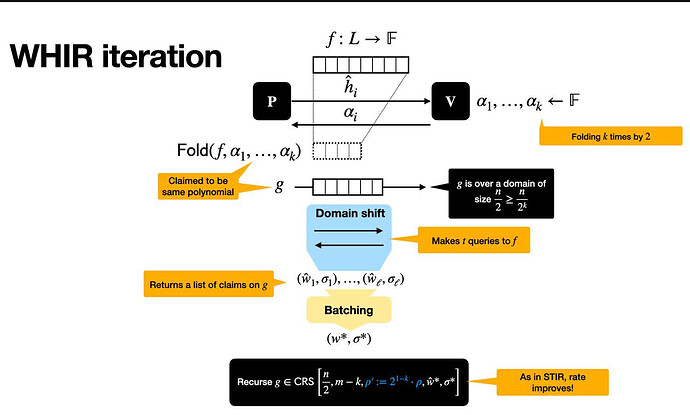
WHIR 迭代總結

如下圖所示，每次 WHIR 迭代都會將接近度測試問題簡化為一個較小的問題，同時保持合理性。

圖片1280×771 91.2 KB

這主要分為三個階段：

設置

我們從一個函數f : \mathcal{L} \to \mathbb{F} f : L → F開始，該函數定義在結構化域\mathcal{L} L （大小為2^m 2 m的乘法子群）上。證明者聲稱f f來自於對多線性多項式\hat{f} ^ f求值，並且該多項式滿足如下約束：

\sum_{\mathbf{b} \in \{0,1\}^m} \hat{w}(\hat{f}(\mathbf{b}), \mathbf{b}) = \sigma,

∑ b ∈ { 0 , 1 } m ^ w ( ^ f ( b ) , b ) = σ ,

其中\hat{w} ^ w是一個簡單的約束多項式。這是我們想要驗證的核心命題。

交互階段

驗證者發送一個隨機挑戰\alpha α ，指示證明者摺疊函數——通過隱藏一個變量將兩個輸入壓縮為一個。這將生成一個新函數f' = \mathrm{Fold}(f, \alpha) f ′ = F o l d ( f , α ) ，該函數定義在較小的域\mathcal{L}^{(2)} L ( 2 )上，並且涉及m - 1 m − 1 個變量，而不是m m 。

為了確保摺疊是誠實進行的，驗證者會執行幾項檢查：

它在域外隨機採樣一個點並要求證明者對其進行評估，確保f' f ′確實來自低次多項式。
它從摺疊函數中採樣一些值，並將它們與f f所說的值進行比較，以強制一致性。
它使用隨機線性組合將所有這些檢查（連同約束）組合成一個方程，併為下一輪準備一個新的約束多項式。

遞歸聲明

在這一輪結束時，驗證者和證明者就一個新的斷言達成一致： f' f ′在更小的定義域和更少的變量上接近於一個新的多項式\hat{f}' ^ f ′ ，並且\hat{f}' ^ f ′滿足一個新的約束：

\sum_{\mathbf{b} \in \{0,1\}^{m-1}} \hat{w}'(\hat{f}'(\mathbf{b}), \mathbf{b}) = \sigma'。

∑ b ∈ { 0 , 1 } m − 1 ^ w ′ ( ^ f ′ ( b ) , b ) = σ ′ 。

這個新實例的形式與原始實例完全相同，只是更小。WHIR 隨後遞歸此斷言，重複相同的步驟，直到函數小到可以直接檢查。

這種方法的妙處在於，每一輪可以一次性去除k個變量，同時僅將域縮小2倍，從而降低驗證率。最終，驗證者可以高度確信原始函數f接近於滿足約束的有效碼字——而這一切都只需付出很少的努力。

WHIR 能為以太坊帶來什麼

WHIR 的獨特之處在於其執行鄰近度檢查的方式。WHIR 並不依賴 FRI 等傳統技術，而是採用基於摺疊加和校驗的遞歸方法，這使得它在多線性設置（其中見證是\{0,1\}^m { 0 , 1 } m上的函數）中尤其有效。這種設計帶來了一些與以太坊及類似鏈上環境尤其相關的優勢。

極低的查詢複雜度。WHIR僅需少量查詢即可執行鄰近度測試。這意味著更少的 Merkle 開啟次數、更少的鏈上數據發送次數，最終顯著降低驗證成本。
快速驗證，通常以微秒到幾毫秒為單位。WHIR專為超快速驗證而設計——使用 Keccak 或 Blake3 等快速哈希函數時，通常在幾百微秒內完成；使用 Poseidon2 等支持 SNARK 的哈希函數時，則最多可在幾毫秒內完成。它通過結合兩個強大的思想來實現這一點：BaseFold 的和校驗協議（以最小開銷驗證多項式恆等式）和 STIR 的遞歸摺疊（壓縮每輪問題規模）。兩者結合，將全局鄰近度檢查分解為一系列易於驗證的較小檢查。
更小的證明。WHIR顯著減少了證明的大小，尤其是在多線性設置下。WHIR 不再將跡的每一列提交為單獨的單變量多項式，而是將整個見證表示為單個多線性多項式\hat{f} ^ f 。只需一次提交，遞歸摺疊可以逐輪減小域的大小。這可以減少提交次數、查詢次數和編碼開銷，即使對於大型計算，也能顯著減小證明大小。
靈活的編碼。WHIR支持單變量和多線性編碼。這使得它與各種 SNARK 結構兼容——無論它們使用傳統的單變量編碼（例如 PLONK 或基於 FRI 的系統），還是多線性方法。

以太坊上的應用

由於其緊湊的證明和微秒級驗證，WHIR 特別適合以太坊應用：

Rollups。Rollups中的狀態轉換可以編碼為多線性多項式。WHIR 有助於簡潔地證明這些轉換，併為以太坊 Layer-1 驗證者提供極快的驗證速度。
簽名聚合：隨著未來對 BLS 簽名後量子時代替代方案的需求，高效驗證數千個基於哈希的簽名至關重要。WHIR 提供的加密引擎可以將這些龐大的集合壓縮為單個恆定大小的證明，並最大程度地減少鏈上驗證佔用的空間。
低 Gas 的 SNARK 驗證：鏈上 Gas 成本主要由數據存儲和計算決定。WHIR 的目標在於最小化查詢複雜度（減少 Merkle 路徑數據）和驗證者的計算工作量。雖然某些前量子 SNARK 仍處於高度優化狀態，但 WHIR 的性能使其成為後量子系統中的領先競爭者，因為在後量子系統中，鏈上效率是不可協商的，正如本研究文章所探討的那樣。

簡而言之，WHIR 是一種快速、遞歸且靈活的鄰近協議，能夠自然地融入現代 SNARK 堆棧。對於以太坊而言，它提供了一條通往更小、更便宜、更快速證明的途徑——尤其是在已經受益於多線性編碼的系統中。

WHIR 與 FRI：近距離測試的代際飛躍

FRI 一直是現代證明系統（尤其是 STARK）的基石。其設計使用遞歸摺疊來有效地測試承諾函數是否接近低次多項式。在經典的 STARK 流程中，首先將所有代數約束組合成一個高次“組合多項式”，然後對其運行 FRI 來證明它實際上是一個具有預期低次的多項式。這種方法非常強大，並確立了使用多對數驗證器進行後量子證明的可行性。

然而，SNARK 設計的格局正在發生變化。像 Jolt、Binius 和 SP1 Hypercube 這樣的現代系統正在從這種兩步“先合併後測試”的模型轉向更集成的多線性方法。在這個新範式中，證明是圍繞和校驗協議構建的，該協議是一種用於驗證多線性多項式聲明的工具。WHIR 正是在此體現了其根本性的演進。

WHIR 重新思考了接近度測試，以適應這個現代的、以和校驗為生的世界。WHIR 不再是處理約束後運行的通用低階測試，而是將約束驗證直接集成到其遞歸過程中。FRI 輪大致包括摺疊域並對隨機點執行一致性檢查。相比之下，WHIR 輪將這種摺疊與輕量級和校驗相結合，這不僅確保摺疊的正確性，還將計算的代數約束傳遞到下一個更小的實例。

這種架構差異帶來了關鍵的性能優勢：

查詢次數漸近減少。這是 WHIR 最大的優勢。對於包含2^ m個元素的計算，FRI 的查詢複雜度隨m m線性增長，而 WHIR 的查詢複雜度隨m m呈對數增長。對於大規模計算而言，這是一個顯著的改進。實際上，這意味著 Merkle 路徑開口次數會大大減少，而 Merkle 路徑開口次數是影響證明大小和鏈上驗證 gas 成本的主要因素。
原生多線性和約束支持。WHIR是約束 Reed-Solomon 碼的近似 IOP。它旨在處理定義現代證明系統的多線性多項式和基於和校驗的關係。雖然 FRI 可以適應這些設置，但 WHIR 將它們視為“一等公民”，從而實現更簡潔、更高效的設計。
極快的驗證速度。更少的查詢次數和基於校驗和的輕量級驗證器邏輯相結合，使 WHIR 能夠實現數百微秒的驗證時間。這使得它非常適合鏈上應用，因為驗證器工作的每一微秒都會直接轉化為用戶成本和網絡吞吐量。

簽名聚合：WHIR 的具體用例

以太坊未來共識層面臨的關鍵挑戰之一是找到一個後量子時代的 BLS 簽名替代方案。目前已探索了多種方案，包括基於格的方案和基於累積的協議，但其中許多方案難以在可擴展性、效率和後量子安全性之間取得平衡。

一個特別有前景的方向是使用XMSS 簽名，它基於哈希值，且設計為量子安全。然而，XMSS 簽名數據量大，單獨驗證成本高昂，因此聚合簽名至關重要。其思路是使用基於哈希值的 SNARK 算法將數千個單獨的簽名壓縮成一個簡潔的證明，然後將其發佈到鏈上。正如這篇以太坊研究文章所述，這樣的協議必須支持兩種操作：

聚合：將大量原始簽名壓縮成一個 SNARK 證明，
合併：遞歸地將兩個現有的聚合證明組合成一個證明。

合併操作引入了遞歸證明要求——而這正是 WHIR 的優勢所在。得益於其摺疊機制和極低的查詢複雜度，WHIR 使得構建小型且易於驗證的 SNARK 變得更加容易。更少的查詢意味著更少的哈希計算，從而直接降低了驗證每一層遞歸的成本。與 FRI 等傳統的 PCS 結構相比，WHIR 能夠實現更快的遞歸證明——這對於實時簽名聚合至關重要。

今日表現及未來展望

在這種情況下，衡量性能的自然方法是每秒可證明的哈希值（例如 Poseidon2）數量。我們目前的 WHIR 實現實現了：

在高端 GPU（RTX 4090）上每秒執行 100 萬次 Poseidon2 哈希運算，
消費級 CPU 上每秒可執行 100,000 次 Poseidon2 哈希運算。

PCS 邏輯 ( WHIR-P3 ) 和 PIOP 層 ( Whirlaway ) 均已公開，並正在積極優化。儘管目前的瓶頸在於 CPU 性能，但目前正在努力達到與 GPU 速度相當的水平——目標是在 CPU 上實現每秒 100 萬次哈希運算，與Plonky3等系統已經實現的水平相當。

總結和後續步驟

WHIR 提供了一種引人注目的全新鄰近度測試方法，尤其適合以太坊的需求：較小的證明大小、快速驗證，以及與單變量和多線性證明系統的無縫集成。其遞歸摺疊策略和通過 sumcheck 進行的約束檢查機制，使其成為現代 SNARK 堆棧的理想之選，尤其是在效率和簡潔性至關重要的應用中——例如 rollups、zkVM 和精益鏈的簽名聚合。

在本文中，我們重點介紹了 WHIR 協議本身及其優勢。但 WHIR 只是完整 SNARK 的一個組成部分。在後續文章中，我們將描述如何圍繞 WHIR 構建一個完整的證明系統，並展示它如何融入基於哈希加密的簽名聚合完整流程。

與此同時，我們正在積極優化我們的實現——旨在使 GPU 和 CPU 的驗證速度達到甚至超越當今最佳系統，同時保持協議的模塊化和易於採用。我們目前維護著一個基於 Plonky3 的開源 WHIR 實現 ( WHIR-P3 )，並計劃將其作為社區驅動的成果直接上傳到Plonky3 。這符合我們將 WHIR 打造成公共產品的願景——開放、集體維護，並易於集成到其他項目中。

目前，一些致力於 zkVM 的團隊已經表示有興趣採用 WHIR，我們相信，隨著以太坊生態系統的發展，將會出現更多的用例。

我們的目標是讓 WHIR 不僅僅是一個快速而優雅的想法，而且成為下一代鏈上證明的實用基石。