作者:NIFTY

Presido Bitcoin 是舊金山的一個 Bitcoin-only 的聯合辦公空間,他們在上週舉辦了一場關於比特幣和量子計算的行業會議。@roasbeef 是 btcd 和 lnd 兩種客戶端軟件的首席維護者,以及 Lightning Labs 的首席技術官。他在會議上提出了一種為比特幣添加量子安全簽名方案 SPHINCS+ 的提議。在今天的報告中,Insider 的協議專家 @niftynei 將為你解讀這個提議。
量子安全問題
比特幣區塊鏈上的大部分資金都是用私鑰來保護的。為了讓區塊鏈確認你的比特幣交易(資金轉移),你需要證明你擁有花費這些資金的權限,具體做法就是提供一個簽名。有效的簽名只能由能夠接觸到正確私鑰的人生成。
從某種意義上來說,比特幣也是 “通過混淆來實現安全性”,這裡的 “混淆” 就是猜測出你的私鑰的難度。可能作為私鑰的數字的數量是天文數字級別。猜測出某個私鑰需要花費許多時間和能量,是任何人在合理的時間範圍內都做不到的(比如需要幾百年時間)。
然而,當前的比特幣密鑰依賴於基於橢圓曲線的數學等式。橢圓曲線是創建公私鑰的明智選擇,因為這樣的公私鑰關係一般來說比質數分解(另一種作為公私鑰密碼學基礎的 “數學系統”)更加安全,公私鑰的體積也更小。
但是,橢圓曲線密碼學也有一個問題。Shor 算法由 Peter Shor 在 1994 年發明,基於傅里葉變換,意味著一臺具有足夠量子比特幣(qubits)的量子計算機(quantum computer)可以快速計算出任何公鑰的私鑰。
Shor 算法意味著我們 知道 如何打破橢圓曲線密碼學,只是能夠做到這件事的工具還不存在。這樣的工具會不會出現、什麼時候會出現,也是一個有很多爭議的話題,不僅出現在比特幣社區中,也出現在廣大的密碼學界。用來保管比特幣的每一個私鑰的安全性,都取決於在無限長的未來、不會有任何人能夠接觸到能夠執行 Shor 算法的工具。
普遍的共識是,到未來的 某個 時間點,比特幣需要遷移到一種 後量子(post-quantum)的公私鑰密碼學系統中。@roasbeef 上週在 Presidio Bitcoin 的提議基於 “SPHINCS+” 哈希簽名方案。我們先來簡單看看它是怎麼工作的,以及為什麼它可能是一個保護比特幣的好選擇。
量子安全,但數據沉重
“SPHINCS+” 是一種基於哈希函數的簽名構造。它的核心是,依賴於密碼學哈希函數(而不是優雅的橢圓曲線等式或者隱秘的大質數分解)來構造公鑰和驗證簽名。基於哈希函數的密碼學方案不受 Shor 算法影響,因為它們在單向函數(one-way functions)背後 不使用 函數式數學系統(functional math systems)。相反,哈希函數依賴於暴力的原像(preimage)數據堆疊。而暴力不包含在量子計算機傅里葉變換面前脆弱的數學關係(或者說捷徑), 也就沒有 Shor 算法可以利用的對象。
堆疊數據,也就是哈希函數,有一個缺點:它的公鑰和簽名需要多得多的數據來分享。中本聰為比特幣選擇了橢圓曲線,正是因為在確認一個簽名以及將資金鎖定到一個公鑰時,基於橢圓曲線的密碼學需要分享的數據 體積較小。我喜歡說,比特幣是橢圓曲線密碼學的殺手級應用(killer app);在中本聰在比特幣協議中使用 secp256k1(具體的一種橢圓曲線)之前,大多數密碼系統都在使用 RSA(或者說質數分解)作為底層的數學系統。根據 SEC 2 參數論文,簽名的安全性要達到 128 比特,RAS 的公鑰需要長達 3072 個比特,而橢圓曲線的公鑰只需要 256 比特。

小體積對區塊鏈系統是非常重要的,因為任何添加到區塊鏈上的數據都必須發送給網絡中的每一個對等節點、由他們存儲。緊湊的簽名和公鑰體積意味著,同樣大小的數據空間可以塞進更多的交易。體積上的節省可以說就是中本聰為比特幣選擇橢圓曲線而不是 RSA 密碼學的理由。
相比之下,後量子的密碼學系統(中的公鑰和簽名)都大得令人難以置信。SPHINCS+ 系統中的公鑰跟比特幣當前的密鑰系統中的公鑰體積一樣大,但簽名的體積達到幾千個字節。隔離見證 v1(也即 Taproot)中的 Schnorr 簽名是 64 字節長;而 SPHINCS+ 的基準測試簽名是 3 ~ 7 千字節。
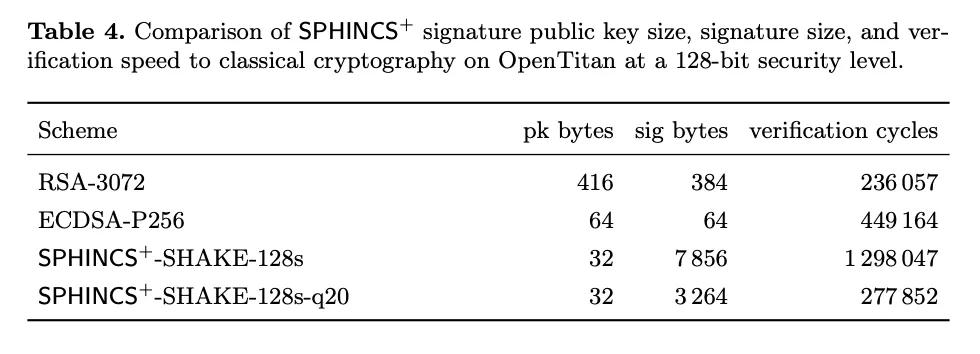
- 來自 NIST SPHINCS+ 參數論文 -
SPHINCS+
SPHINCS+ 是一種複雜的簽名方案,是用多層的後量子簽名 “小工具” 開發出來的;將它們結合在一起之後,SPHINCS+ 就創造了一種量子安全的 公鑰/私鑰 對,可以安全地簽名許多消息。與它的前輩 “XMSS(eXtended Merkle Signature Schemes)” (也是一種基於哈希函數的後量子簽名方案)不同,在 SPHINCS+ 中,你不再需要為一個密鑰對記憶曾經制作過的簽名。
一個 SPHINCS+ “結構” 可以製造一個公鑰,這個公鑰可以簽名多條消息而不會揭曉私鑰。
而一個 SPHINCS+ “結構” 由以下三個部分組成:
FORS,即 “隨機子集森林(Forest of Random Subsets)”。這是 SPHINCS+ “結構” 的底層,也是用消息來確定要揭曉哪些原像的地方。被揭曉的原像集合將成為 SPHINCS+ 簽名的基礎。在 SPHINCS+ 中,消息實際上是使用 FORS 來 “簽名” 的。下一部分將用來把 FORS 簽名綁定到 SPHINCS+ “超級結構(super structure)”(我選擇這麼稱呼它)的根公鑰上。
WOTS+,即 “Winternitz 一次性簽名+”。這是一種後量子的、基於哈希函數的簽名算法,可以安全地簽名一條消息。SPHINCS+ 使用 WOTS+ 簽名將在 FORS 中揭曉的原像綁定到分層的 XMSS 默克爾樹上。這棵分層的默克爾樹的樹根即是 SPHINCS+ 公鑰。(WOTS 和 WOTS+ 的唯一區別在於,這個帶有 “+” 的變種在每一次哈希運算中都包含了一個隨機前綴,從而緩解了 “多目標哈希攻擊(multi-target hash attacks)”。“SPHINCS+ ” 中的 “+” 也同樣意味著,每一次哈希運算中都包含一個隨機生成的前綴。)
XMSS 默克爾樹。一棵 XMSS 默克爾樹的每個葉子上都是一個 WOTS+ 公鑰。SPHINCS+ 用 XMSS 默克爾樹所構成的層級創建了巨大的金字塔結構。樹之上的樹通常被稱為 “hypertrees(超級樹)”。父樹的每一個葉子都是一個 WOTS+ 公鑰,這個公鑰要來簽名在它之下的樹的樹根,就這樣將樹綁定在一起(從而形成一個結構)。樹的數量以及層級的數量,都是可以改變的,取決於一個 SPHINCS+ “超級結構” 想要的簽名大小。要求的簽名體積越小,驗證和生成簽名所需的哈希次數就越多。所有樹的最低層的每一個葉子都是一個 FORS 。許多默克爾樹以及許多層級,意味著金字塔的底部有許許多多的 FORS,可以用來製作重用概率非常小的安全簽名。
(譯者注:這裡之所以將一個 SPHINCS+ 結構稱為 “金字塔” 而不是 “一整棵樹”,是因為它確實不像單棵默克爾樹那樣,完全由葉子開始逐級合併、最終形成一個樹根(從而一個樹根就承諾了底層的所有葉子);相反,頂層的一棵 XMSS 默克爾樹的每個葉子是一個 WOTS+ 公鑰,每個 WOTS+ 公鑰都 簽名 第二層某一棵 XMSS 默克爾樹的樹根,這些第二層 XMSS 默克爾樹也是同樣的構造:每個葉子是一個 WOTS+ 公鑰;依此類推;因此,下一層的 XMSS 默克爾樹的數量總是上一級數量的倍乘,也就是一個金字塔。最底層的不是 XMSS 默克爾樹,而是 FORS 默克爾樹(森林) —— 一個 FORS 公鑰會對應許多棵默克爾樹,可用來製作簽名。)
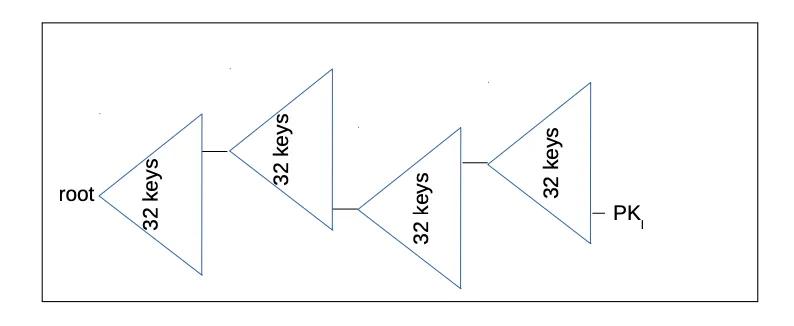
- 超級樹圖的過度簡化版本。上圖中的 PK 在 SPHINCS+ 語境下實際上是 FORS 簽名。而 “root” 是 SPHINCS+ 公鑰。 -
生成一個 SPHINCS+ 公鑰的基本流程是:生成放在樹根中的 WOTS+ 公鑰,然後計算這些樹的默克爾根(譯者注:原文如此;疑應為 “生成放在葉子中的 WOTS+ 公鑰,然後計算這些樹的默克爾根”)。最頂部的一棵樹的樹根就是 SPHINCS+ 公鑰。默克爾樹的樹根的體積由用來計算這個樹根的哈希函數決定。一般來說,我們選擇使用 SHA256 哈希函數,其輸出是 256 比特。這就意味著,這樣一棵默克爾樹的樹根將是 32 字節。這就是 SPHINCS+ 公鑰的由來。
生成一個 SPHINCS+ 簽名需要使用消息的一個哈希值,以隨機選擇要連接到 SPHINCS+ 超級樹、生成 FORS 簽名的 FORS 子樹。一旦 FORS 簽名生成之後,再用上一層 XMSS 樹中的一個 WOTS+ 公鑰的私鑰來簽名它;如此,簽名與(公鑰的)默克爾路徑結合起來,一層一層向上,直到抵達最頂端的 SPHINCS+ 公鑰。所有的 WOTS+ 簽名、FORS 簽名,以及讓它們從 FORS 簽名走向 SPHINCS+ 公鑰的默克爾路徑,就是這條消息的簽名。你可以想象,這是很大一堆數據, 這就是為什麼 SPHINCS+ 簽名要比橢圓曲線簽名(64 字節)大上幾個數量級的原因。
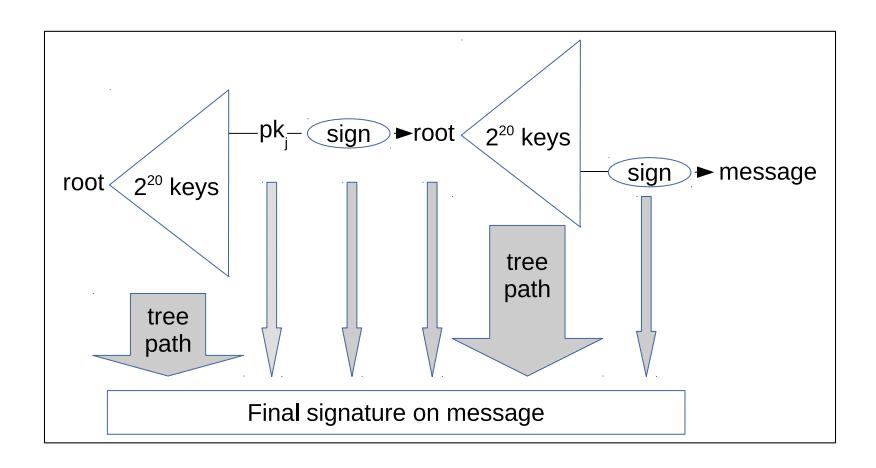
- 包含再 SPHINCS+ 簽名中的數據的示意圖;右邊的 “sign” 會生成一個 FORS 簽名;而中間的 “sign” 會生成一個 WOTS+ 簽名。 -
為什麼要使用 SPHINCS+ ?
SPHINCS+ 是充分分層的,它非常笨拙,而且依賴於多種不同的 “工具” 來生成簽名:Witnernitz 簽名、FORS 和 XMSS 子樹。
SPHINCS+ 的複雜性來源於它強大的特性集合。它是對 XMSS 的嚴格優化。XMSS 也是一種後量子的簽名方案,允許一個公鑰簽名多條消息,但你必須跟蹤已經用來簽過名的默克爾樹葉子。SPHINCS+ 則使用從被簽名消息的摘要中生成的隨機性,確定性地選擇超級樹上的一個子樹葉子。
在比特幣中,理想情況下,你應該為每一筆交易輪換一個公鑰,這意味著你要為 每一個 在比特幣中使用的公鑰生成一個新的 SPHINCS+ 超級結構。
一開始,我困惑於為什麼要在(理想情況下)一次性的公鑰上提供這麼強大的多次簽名功能。
來自 Blockstream Research 的 Jonas Nick 指出,你會在想要追加手續費或者交易因為某些原因而丟失時再次簽名;Laolu(也就是 roasbeef)指出,閃電網絡這樣的鏈下協議,需要(同一公鑰)多次簽名以跟蹤私人合約內的狀態轉換。
在比特幣上你可能不需要無限的重複簽名功能,這就允許我們構造規模更小的 SPHINCS+ 超級結構來生成公鑰。更小的超級結構意味著簽名的體積會更小,因為需要攜帶的默克爾樹路徑減少了。但同時,這也意味著,在安全性開始下降之前,你可以製作的簽名的數量變少了。在橢圓曲線密碼學中,簽名 nonce 的複用會立即洩露私鑰;而在 SPHINCS+ 中,公鑰的過度使用(用於簽名),只會讓安全性從 128 比特開始逐漸降級(隨著低層的 FORS 開始部分複用)。
在深入研究之後,我不得不說,我真的成了 roasbeef 的使用 SPHINCS+ 作為後量子簽名方案的提議的支持者。為了確定具體的參數,還有許多設計工作要做。我期待有一個 BIP 草稿(他表示已在撰寫中),可以幫助填補一些圍繞超級結構的層數與安全重複簽名次數關係的空白。
還值得指出的是,就像 roasbeef 的演講提到的,SPHINCS+ 不允許使用 種子詞/子密鑰 派生路徑。這意味著 BIP32 層級式錢包會死去。這裡還有別的選擇,但我們將失去使用層級式派生路徑來描述組成一個錢包的公鑰的辦法(當前的 xpub 和子錢包行業習慣就是這個作用)。
該走哪條路呢?
比特幣將遷移到一種後量子簽名方案。什麼時候、使用哪種方案、什麼參數,可能是接下來幾年的熱門話題。
Roasbeef 的 SPHINCS+ 提議是一種吸引人的選項,儘管多層樹超級結構非常複雜。在我看來,所有基於哈希函數的後量子公鑰方案都非常猙獰。SPHINCS+ 也醜陋,但這是因為它提供了最多的特性,尤其是重複簽名時候的 “無狀態性(statelessness)”(譯者注:也可譯為 “免記憶性”)。
隨著我更加理解每一部分在協議中扮演的角色,我開始強烈讚賞這種設計出這種多層結構的聰明。
Roasbeef 在編寫 BIP 上還有許多工作要做,尤其是在選擇每一棵樹的深度以及子樹的層數上,還有 Winternitz 簽名的體積以及 FORS 的參數。簽名的體積和生成簽名所需的哈希次數之間存在兩難。要先在計算量和鏈上蹤跡之間找出正確的平衡,才能發佈正式的 BIP 。
那麼還剩最後一個問題:
遷移到 SPHINCS+ 是否意味著比特幣成了一種金字塔騙局(pyramid-scheme)?很難定義,但看起來的確是這樣。
(譯者注:這裡是一語雙關的玩笑,因為 “pyramid-scheme” 既可以表示 “金字塔騙局” ,又可以指代 SPHINCS+ 的 “金字塔結構”。)
致謝
感謝 Jonas Nick 和 Olaoluwa Osuntokun 在解釋 SPHINCS+ 公鑰複用和參數調整上的幫助。
進階閱讀
想要更加深入?以下是一些很好的材料,也是我撰寫這篇文章的資料來源:
- Laolu 在 7 月 17 日的 Presidio Bitcoin 比特幣與量子計算會議上的演講幻燈片
- Sphere10 的 Winternitz 簽名講解,讓我掌握了後量子簽名的基礎知識
- 來自軟件開發者 Ethan Rahn 的一篇深度講解博客,包含了很好的示意圖,以及一些後量子簽名的開發歷史
- SPHINCS+ 的極佳深度講解,來自 NIST 的 John Kelsey。是我看過最好的詳盡解釋,但顯然被埋沒了。
(完)