從 Pedersen 承諾範圍證明中移除配對、防彈證明或 ZKP

TL;DR

簡化範圍證明。在 EVM 上驗證基於 Pedersen 承諾的隱私幣的範圍證明，僅需 6 個 ECMUL 和 3 個 ECADD（37,000 Gas）。首次設置和承諾需要 zkSNARK，但之後成本將降至最低。客戶端每次生成交易時，也無需進行 ZKP 計算。

包含安全證明的完整論文： https://eprint.iacr.org/2025/1811.pdf

步驟：

G、H、B 是曲線上的獨立點。

為每個證明者（代幣發送者）進行一次性設置

1. 採樣 a ← Zq 並設置公共錨點 U = aB。
2. 使用曲線上的點構建一棵 Merkle 樹。對於每個 X ∈ {1, . . . , 2 n}，定義葉子節點 aXG
3. 使用 NIZK 上鍊，證明由 aXG 組成的樹的 Merkle 根。（預範圍證明）

無標題演示文稿 (11) 960×540 20.3 KB

證明（發送令牌時）

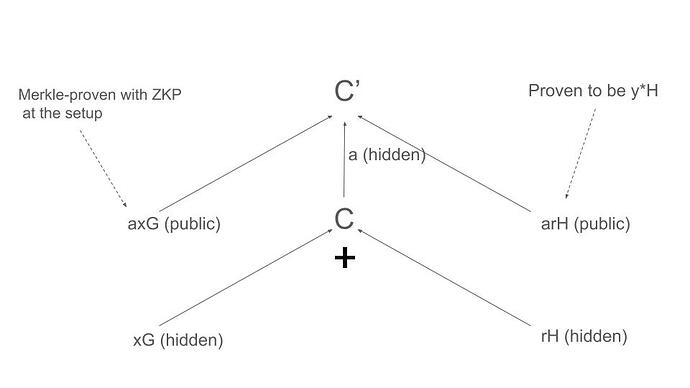
1. 做出 Pedersen 承諾 C = xG + rH，其中代幣數量為 x，隱藏 r。（x、r、xG 和 rH 不應暴露）
2. 提交 C, C' = aC, axG 及其 Merkle 證明、(U, B) 和 (C', C) 的 Chaum-Pedersen DLEQ 證明、arH 和 Schnorr 協議的 (arH, H) 證明

驗證（C 和 x 是否在 EVM 的範圍內）

1，使用 Chaum-Pedersen DLEQ 檢查 (U, B) 和 (C', C) 是否具有相同的離散
2. 使用 Schnorr 協議或 ECDSA 檢查證明者是否可以從 H 得出 arH。
3. 在設置樹中檢查axG的Merkle Proof。
4. 檢查 C' = axG + arH

## 為什麼需要 Chaum-Pedersen DLEQ 和 U=aB
如果我們使用 Schnorr 協議或 ECDSA 來檢查 (C', C) 的關係，惡意證明者可以使 C' = yC 和 C = (bigX)G + rH，其中 y = ax/(bigX)。yrH 也將被驗證。

如何讓樹變小

用隨機數創建一棵包含所有金額的樹會有點挑戰性。用有限的隨機數創建一棵點樹，用標量乘以葉子節點，並在鏈上添加一個點，會很有幫助，因為沒有人能從樹曲線上的點猜出隨機數。