私人多重簽名 v0.1

avatar
Ethereum Research
10-16
本文為機器翻譯
展示原文

這是我花了一段時間才實現的。雖然不完美，但已經儘可能地實現了隱私保護的多重簽名。期待您的反饋！

請查看我的其他相關研究論文： 《Confidential Wrapped Ethereum》和《ZEX：Confidential Peer-to-Peer DEX》 。

另外，請看一下宏偉的以太坊隱私路線圖。

抽象的

本文提出了一種基於零知識 (ZK) EVM 的多重簽名錢包的實用實現方法，以保護集體決策的隱私和機密性。該方法結合了三個核心特性：用於匿名性的 Merkle 樹成員身份證明；用於無偏見決策的聚合 ECC ElGamal 加密，以確保參與者投票的機密性；以及用於在密鑰推導和消除中心化可信實體時實現非交互性的分佈式密鑰生成 (DKG)。

所提出的解決方案由 Solidity 智能合約和零知識證明電路組成。前者充當賬戶工廠的角色，並充當用戶與之交互以創建多重簽名和執行集體提案的實際賬戶。後者負責檢查用戶是否屬於多重簽名集，並驗證他們是否執行提案的決定，且不透露中間結果。

所提出方法的缺點是，所有多重簽名參與者必須對提案進行投票才能計算其結果。

1. 簡介

公鏈的透明度帶來了諸多優勢，包括增強操作的可追溯性、執行的可驗證性以及數據開放性，使每個人都能訪問。然而，它在多方決策方面也帶來了獨特的挑戰，尤其是在保護隱私和防止投票偏見方面——而這正是安全公正的多重簽名錢包的基本要素。

目標是創建一個簡單的、無需許可的多重簽名，它不會透露任何有關其成員的信息，並向多重簽名選民保證他們的選票是秘密的，並且他們的選擇不會受到早期參與者投票方式的影響。

多重簽名將允許用戶加入/退出成員列表、配置“簽名閾值”以及執行集體批准的交易，且幾乎不會損害隱私。此外，在成員列表中的所有用戶都投票之前，用戶可以在不瞭解個人投票或結果的情況下對提案進行投票支持或反對。

當然，重要的限制是，最後一位投票參與者將能夠在投票和披露投票之前解密並查看正在進行的提案方向。

2. 規格

2.1. 申請流程

在深入技術探討之前，有必要先了解一下整體架構並理解基本的應用程序流程。本文提供了多重簽名錢包創建、提案創建以及包含提案投票的通用多重簽名交易執行流程。

2.1.1. 多重簽名創建

該應用程序的基石是多重簽名錢包。用戶與應用程序交互時，會根據允許投票者的列表創建多重簽名，以滿足其業務邏輯。

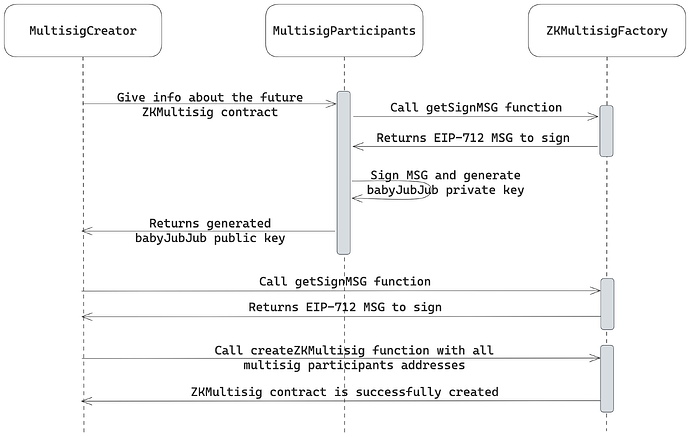
多重簽名創建流程如下圖所示：

圖 1：ZKMultisig 合約創建流程
圖1：ZKMultisig合約創建流程3159×2003 245 KB

  1. 創建流程始於用戶（錢包創建者）收集待添加到允許列表中的投票者的公鑰。由於多重簽名使用零知識證明來保護隱私，所有用戶在使用應用程序之前都必須創建一個特殊的 babyJubJub 密鑰對，作為其唯一標識符。

    要創建這些密鑰，用戶需要使用其以太坊（ECDSA）私鑰對 EIP-712 結構化消息進行簽名，並對獲得的簽名進行哈希處理。生成的哈希值即為 babyJubJub 私鑰。

    用戶可以選擇簽署唯一消息以獲取他們願意參與的每個多重簽名的唯一公鑰（增加隱私），或者使用“默認”消息堅持使用單個公鑰以在整個平臺上使用（可能更好的用戶體驗）。

  2. 獲取所有必要的 babyJubJub 公鑰後，錢包創建者會調用ZKMultisigFactory智能合約上的錢包創建函數，提供所有需要添加到允許列表中的公鑰。多重簽名機制在底層將參與者信息存儲在稀疏 Merkle 樹 (SMT) 數據結構中，從而實現零知識證明的成員資格證明和低成本的列表維護。

  3. 多重簽名錢包部署後，其成員可以通過生成 ZK 成員資格證明並應用 EdDSA 盲注器來創建提案並對其進行投票，以實現決策不可重用性。

通過所描述的方法，我們可以通過確定性密鑰派生函數（KDF）將用戶的真實“錢包地址”抽象為 babyJubJub 地址，從而為用戶實現完全隱私，並將確定決策地址的概率從 1 降低到1/N 1 / N ，其中N N是多重簽名成員的數量。

2.1.2 提案創建

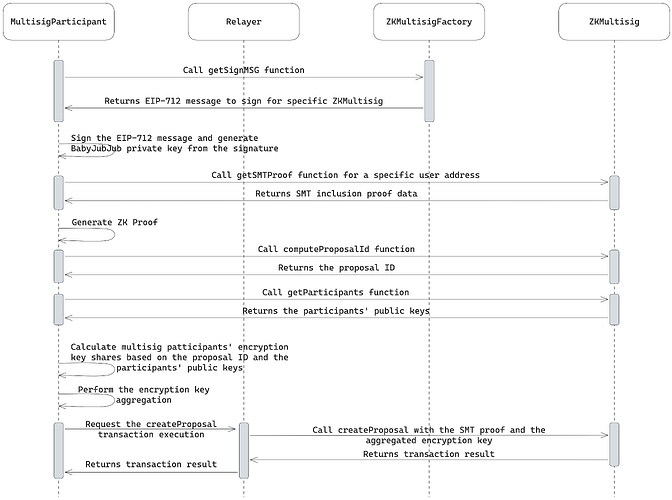
提案創建流程如下圖所示：

圖 2：多重簽名提案創建流程
圖 2：多重簽名提案創建流程4360×3240 434 KB

  1. 提案創建者（來自多重簽名允許列表中的用戶）通過從“多重簽名錢包創建”步驟中確定性地恢復 babyJubJub 密鑰對來登錄應用程序。

    KDF 算法保持不變。從ZKMultisigFactory獲取 EIP-712 結構化消息，然後對其進行簽名，並對簽名進行哈希運算，計算出 babyJubJub 私鑰。

  2. 用戶生成一個 ZK 證明，該證明通過 SMT 包含證明無需許可地驗證他們在多重簽名中的成員資格。

  3. 提案創建者計算提案的 ID，用於生成一次性聚合加密密鑰。

  4. 創建者根據提案 ID 和參與者的 babyJubJub 公鑰，使用 KDF 以非交互方式計算每個多重簽名參與者的加密密鑰份額。

  5. 在計算出所有加密密鑰份額後，創建者將它們聚合成最終的加密密鑰。

  6. 提案創建者通過中繼器調用createProposal函數，提供 SMT 包含證明和聚合密鑰，以便進一步用於投票加密。

提案創建後，多重簽名參與者可以開始投票。

2.1.3. 對提案進行表決

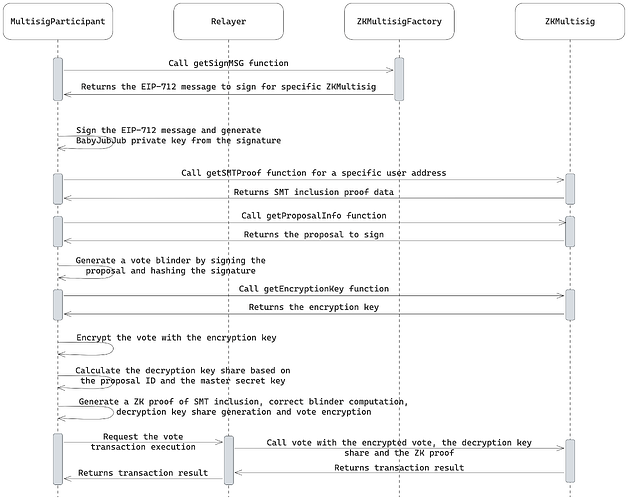
提案投票流程如下圖所示：

圖 3：多重簽名提案投票流程
圖 3：多重簽名提案投票流程4120×3280 468 KB

  1. 從合同中獲取 SMT 包含（Merkle）證明，以表明用戶是多重簽名的成員。

  2. 用戶使用 babyJubJub 私鑰對要投票的提案進行簽名，並通過對獲得的 EdDSA 簽名進行哈希運算來生成盲注。該盲注用於驗證用戶之前是否曾對同一提案進行投票。

  3. 用戶獲取提案的加密密鑰。

  4. 收到的臨時加密密鑰用於加密他們的投票。

  5. 根據提案 ID，用戶使用其 babyJubJub 私鑰和 KDF 計算解密密鑰份額。

  6. 在計算完所有需要的數據後，多重簽名參與者通過中繼器調用vote功能，提供加密投票、解密密鑰共享和 ZK 證明。

  7. 智能合約將提供的解密密鑰份額添加到可聚合的最終解密密鑰中，並將投票設置為成功投票。

2.1.4 投票披露和提案執行

只有當最後一位參與者投票後，解密密鑰才算完整，並可用於揭示投票結果。這通過調用reveal函數來完成。該函數解密彙總的投票，並根據投票結果更改提案狀態。如果“贊成”票數超過“簽名閾值”，則該提案被設置為“接受”並可執行；否則，則設置為“拒絕”。

下圖說明了投票披露過程，將解密和執行邏輯封裝到單個函數revealAndExecute中。

圖 4：多重簽名提案投票揭示流程
圖 4：多重簽名提案投票揭示流程2390×1540 169 KB

2.2. 加密數學

本節提供了協議中使用的投票加密邏輯的數學基礎。

2.2.1. 橢圓曲線算術運算

在本文檔的上下文中，某些操作是在橢圓曲線上執行的，並且涉及不同於傳統算術的特定數學運算：

  • 點加法P + Q P + Q ，其中P P和Q Q是橢圓曲線上的點，按照定義的群運算邏輯執行。
  • 標量乘法k \times P k × P ，其中k k是標量， P P是橢圓曲線上的一個點，涉及將點P P與自身相加k k次。
  • 點減法P - Q P − Q ，其中P P和Q Q是橢圓曲線上的點，並且與P + (-Q) P + ( − Q )相同，其中-Q − Q是點Q Q的逆。

2.2.2. 加密密鑰的 KDF

該協議使用隱形密鑰方案 CoM17 [1] 作為確定性密鑰分配函數 (KDF)。該方案能夠根據主密鑰生成唯一的密鑰共享，用於加密和解密每個提案的投票。

主密鑰對必須滿足以下條件：

pk = sk \times G ， pk = sk × G ，

其中pk p k — 主公鑰，
sk s k — 主密鑰，
G G — 橢圓曲線上的基點。

在創建錢包時生成的 babyJubJub 密鑰對將用作主密鑰對，ElGamal 加密密鑰和解密密鑰由此派生。密鑰派生過程如下所述。

首先，根據提案 ID 計算挑戰。需要注意的是，多重簽名機制有意省略了提案的增量枚舉，以防止零知識證明重放和搶先交易攻擊。這是通過要求提案創建者簽署其所創建提案的挑戰來實現的。提案 ID 和挑戰的確定性計算方式如下：

 proposalId = keccak256(abi.encode(target, value, data, salt));challenge = poseidon(uint248(keccak256(abi.encode(chainid, zkMultisigAddress, proposalId))));

令r r等於挑戰， R R為挑戰點：

R = r \times G R = r × G

加密密鑰共享的推導如下：

P_i = poseidon(r \times pk_i) \times G + pk_i P i = p o s e i d o n ( r × p k i ) × G + p k i

相應地，解密密鑰份額推導如下：

x_i = (poseidon(sk_i \times R) + sk_i) \mod n x i = ( po o s e i d o n ( s k i × R ) + s k i )模組n

其中n n — 橢圓曲線的階。

密鑰派生方案的一致性可以通過以下方式證明：

P_i = x_i \times G = (poseidon(sk_i \times R) + sk_i) \times G = P i = x i × G = ( p o s e i d o n ( s k i × R ) + s k i ) × G =
= poseidon(sk_i \cdot r \ times G ) \ times G + sk_i \ times G = poseidon ( r \ times pk_i ) \ times G + pk_i = poseidon ( ski⋅r × G ) × G + ski × G = poseidon ( r × pki ) × G + pki

2.2.3. ECC ElGamal加密方案

該協議利用 ElGamal 加密方案 [2] 的橢圓曲線密碼學 (ECC) 修改來加密並解密多重簽名投票。

聚合加密密鑰P P是通過對所有加密密鑰份額求和計算得出的橢圓曲線上的一個點：

P = \sum_{i=1}^N P_i， P = ∑ N i = 1 P i ，

其中N N — 多重簽名參與者的數量，
P_i P i — 加密密鑰共享（橢圓曲線點）。

參與者的投票被映射到橢圓曲線上的點M M 。生成點G G用作“贊成”票，無窮遠點用作“反對”票。選擇一個滿足0<k< n的隨機值k k 。之後，計算密文 ( C_1 C 1 , C_2 C 2 )：

C_1 = k \times G C 1 = k × G
C_2 = M + k \times P C 2 = M + k × P

要解密投票，首先計算聚合解密密鑰份額：

x = \sum_{i=1}^N x_i \mod n, x = ∑ N i = 1 x i模組n ，

其中n n — 橢圓曲線的階，
x_i x i — 解密密鑰共享（標量）。

然後使用計算出的聚合解密密鑰x x恢復消息點M M ：

M = C_2 - x \times C_1 M = C 2 − x × C 1

ECC ElGamal方案中密鑰聚合的一致性可以證明如下：

P = \sum_{i=1}^N P_i = \sum_{i=1}^N x_i \times G P = ∑ N i = 1 P i = ∑ N i = 1 x i × G

D = x \times C_1 = \sum_{i=1}^N x_i \times C_1 = \sum_{i=1}^N x_i \cdot k \times G = k \times (\sum_{i=1}^N x_i \times G) = k \times P D = x × C 1 = ∑ N i = 1 x i × C 1 = ∑ N i = 1 x i ⋅ k × G = k × ( ∑ N i = 1 x i × G ) = k × P

M = C_2 - D = M + k \times P - k \times P M = C 2 − D = M + k × P − k × P

2.2.4. 投票的同態聚合

使用點G和無窮遠點作為投票，可以同態地形成累積投票結果，將每次投票期間的加密投票相加：

SC_1 = \sum_{i=1}^N C_{1_i} S C 1 = ∑ N i = 1 C 1 i
SC_2 = \sum_{i=1}^N C_{2_i} S C 2 = ∑ N i = 1 C 2 i

解密總和得到聚合結果T T ：

T = \sum_{i=1}^N M_i = SC_2 - x \ times SC_1 T = ∑ N i = 1 M i = SC 2 − x × SC 1

解密後的總數T T等於v \times G v × G ，其中v v是投票“支持”該提案的選民總數。

為了揭示投票結果，多重簽名參與者必須循環遍歷鏈下可能的標量值v_i v i ，其中0 \leq v_i \leq N 0 ≤ v i ≤ N ，以找到滿足以下等式的值：

v_i \times G = T v i × G = T

然後他們將這個值提交給智能合約，在那裡檢查上述等式。

  • 如果v < signaturesQuorum v < s i g n a t u r e s Q u o r u m ，則表示沒有足夠的參與者對該提案投“贊成票”，其狀態設置為“拒絕”；
  • 如果v \geq signaturesQuorum v ≥ sign u n a t u r e s Q u o r u m ，則有足夠多的參與者對該提案投了贊成票，其狀態設置為“已接受”。

2.2.5. 加密密鑰鏈上計算

當提案被創建時，必須檢查聚合加密密鑰是否是根據各個公鑰和質詢正確計算出來的。

由於該值是公開可計算的，因此可以通過循環遍歷參與者的主公鑰並得出其加密份額來在智能合約上進行評估。然而，這種方法並非最優，可以通過引入累積公鑰（表示所有參與者主公鑰的總和）來改進。該密鑰存儲在智能合約中，並且每次更新成員列表時都必須更新。

無需為每個參與者單獨計算加密密鑰份額：

P_i = poseidon(r \times pk_i) \times G + pk_i P i = p o s e i d o n ( r × p k i ) × G + p k i

只需計算哈希部分並將其添加到先前哈希的總和中就足夠了，從而減少循環內的操作數：

sumHash = sumHash + poseidon ( r \ times pk_i ) s u m H a s h = s u m H a s h + poseidon ( r × p k i )

然後可以按如下方式計算聚合加密密鑰：

aggKey = sumHash \times G + cumulativePk a g g K e y = s u m H a s h × G + c u m u l a t i v e P k

2.3. 功能

本節提供智能合約和電路的技術描述。本節概述了實現可行原型所需的組件支持功能。

2.3.1. ZKMultisigFactory

該應用程序中有兩個合約： ZKMultisigFactory和ZKMultisig 。工廠合約用於創建多重簽名錢包並生成密鑰派生過程所需的 EIP-712 消息。ZKMultisig 是ZKMultisig本身的實現。

ZKMultisigFactory接口定義如下：

 interface IZKMultisigFactory {event ZKMultisigCreated(address indexed zkMultisigAddress,uint256[2][] initialParticipants,uint256 initialQuorumPercentage);function createZKMultisig(uint256[2][] calldata participants,uint256 quorumPercentage,uint256 salt) external returns (address);function computeZKMultisigAddress(address deployer,uint256 salt) external view returns (address);function getKDFMSGToSign(address zkMultisigAddress) external viewreturns (bytes32);function getDefaultKDFMSGToSign() external view returns (bytes32);function isZKMultisig(address multisigAddress) external view returns(bool);}

ZKMultisigFactory並不直接部署錢包，而是部署 ERC-1967 代理。此外，它採用 create2 方法預先建立 KDF 消息，以確保錢包地址的確定性。

create2中的salt定義如下：

 realSalt = keccak256(abi.encode(msg.sender, salt));

用戶可以決定簽署哪個 KDF 消息：

  • 每個錢包的唯一消息（增加隱私假設）；
  • 默認的（可能用戶體驗更好）。

返回消息的結構可以在第 2.3.6 節中找到。

2.3.2 ZKMultisig

ZKMultisig是一個實現多重簽名功能的合約。該功能包括多重簽名參與者的管理、法定人數設置、提案的創建、投票及其執行。ZKMultisig ZKMultisig定義如下：

 import "@solarity/solidity-lib/libs/data-structures/SparseMerkleTree.sol";interface IZKMultisig {enum ProposalStatus {NONE,VOTING,ACCEPTED,REJECTED,EXPIRED,EXECUTED}struct ZKParams {uint256[2] a;uint256[2][2] b;uint256[2] c;uint256[] inputs;}struct ProposalContent {address target;uint256 value;bytes data;}struct ProposalInfoView {ProposalContent content;ProposalStatus status;uint256 proposalEndTime;uint256 votesCount;uint256 requiredQuorum;}event ProposalCreated(uint256 indexed proposalId, ProposalContent content);event ProposalVoted(uint256 indexed proposalId, uint256 voterBlinder);event ProposalExecuted(uint256 indexed proposalId);function addParticipants(uint256[2][] calldata participantsToAdd) external;function removeParticipants(uint256[2][] calldata participantsToRemove) external;function updateQuorumPercentage(uint256 newQuorumPercentage) external;function create(ProposalContent calldata content,uint256 duration,uint256 salt,ZKParams calldata proofData) external returns (uint256);function vote(uint256 proposalId,bytes calldata encryptedVote,uint256 decryptionKeyShare,ZKParams calldata proofData) external;function reveal(uint256 proposalId, uint256 approvalVoteCount) external;function execute(uint256 proposalId) external;function revealAndExecute(uint256 proposalId,uint256 approvalVoteCount) external;function getPerticipantsSMTRoot() external view returns (bytes32);function getParticipantsSMTProof(bytes32 publicKeyHash)external view returns (SparseMerkleTree.Proof memory);function getParticipantsCount() external view returns (uint256);function getParticipants() external view returns (uint256[2][] memory);function getProposalsCount() external view returns (uint256);function getProposalsIds(uint256 offset, uint256 limit)external view returns (uint256[] memory);function getQuorumPercentage() external view returns (uint256);function getEncryptionKey(uint256 proposalId) external viewreturns (uint256[2] memory);function getProposalInfo(uint256 proposalId) external viewreturns (ProposalInfoView memory);function getProposalStatus(uint256 proposalId) external viewreturns (ProposalStatus);function getProposalChallenge(uint256 proposalId)external view returns (uint256);function computeProposalId(ProposalContent calldata content,uint256 salt) external view returns (uint256);function isBlinderVoted(uint256 proposalId,uint256 blinderToCheck) external view returns (bool);}

在createProposal函數中，驗證給定提案的 ElGamal 加密密鑰聚合至關重要。智能合約必須循環遍歷活躍成員的主公鑰，得出他們的加密密鑰份額，然後將其聚合到加密密鑰中（參見 2.2.5 節）。

2.3.3 提案創建電路

本文中的每個參數都旨在可證明並與零知識電路兼容。提案創建證明的電路信號列表如下：

公共信號：

  • SMT 根（輸入）；
  • 提案 ID（輸入）。

私人信號：

  • 主密鑰；
  • 主公鑰[可選]；
  • SMT 包容性證明。

利用這些信號，電路必須具有以下約束：

  • 所提供的主密鑰確實是所提供的主公鑰的密鑰。
  • 主公鑰屬於 SMT，錨定於 SMT 根。

2.3.4. 提案投票電路

提案投票證明的電路信號列表如下：

公共信號：

  • 用戶盲區（輸出）；
  • 解密密鑰共享（輸出）；
  • 加密點C_1 C 1 （輸出）；
  • 加密點C_2 C 2 （輸出）；
  • 聚合加密密鑰（輸入）；
  • 提案挑戰（輸入）；
  • SMT 根（輸入）。

私人信號：

  • 主密鑰；
  • 主公鑰[可選]；
  • EdDSA 主控對挑戰進行簽名；
  • 實際投票：點G G或inf i n f ；
  • 隨機加密值k k ；
  • SMT 包容性證明。

利用這些信號，電路必須具有以下約束：

  • 所提供的主密鑰確實是所提供的主公鑰的密鑰。
  • 主公鑰屬於 SMT，錨定於 SMT 根。
  • 挑戰的 EdDSA 主簽名根據主公鑰進行驗證。
  • 簽名的波塞冬哈希等於用戶盲注。
  • 根據主密鑰和提議挑戰，可以正確計算解密密鑰份額（參見第 2.2.2 節）。
  • 提供的投票要麼等於G G ，要麼等於inf i n f 。
  • 給定聚合加密密鑰、隨機加密值k k和投票，加密已正確執行（參見第 2.2.3 節）。

2.3.5. 密鑰衍生函數

密鑰派生函數 (KDF) 是一種根據某個輸入確定性地創建 babyJubJub 私鑰的函數。在我們的例子中，輸入是 EIP-712 格式消息的以太坊 ECDSA 簽名。

KDF定義如下：

 message = getKDFMSGToSign() or getDefaultKDFMSGToSign();signature = eth_signTypedData_v4(message);privateKey = keccak256(keccak256(signature));

請注意，切勿洩露簽名，因為私鑰直接來源於簽名。

2.3.6. KD EIP-712 消息

為了創建密鑰派生 EIP-712 消息，需要使用包含合約ZKMultisig地址的 KDF 消息類型哈希。由於網絡和合約信息已包含在標準 EIP-712 域結構中，因此這已足夠。

 bytes32 KDF_MSG_TYPEHASH = keccak256("KDF(address zkMultisigAddr)");bytes32 kdfStructHash = keccak256(abi.encode(KDF_MSG_TYPEHASH, zkMultisigAddress));

getKDFMSGToSign()和getDefaultKDFMSGToSign()函數如上所述創建 EIP-712 消息。getDefaultKDFMSGToSign getDefaultKDFMSGToSign()函數使用零地址來構造默認消息。

2.3.7. 中繼器

由於上述方法完全獨立於交易發送的 EVM 地址，用戶可以使用不同的中繼器來保持匿名。可以使用協議友好的中繼器（例如 GSN），但這需要在前端添加額外的集成邏輯。

3. 基本原理

之所以選擇 ElGamal 加密方案 [2] 的 ECC 修改版，是因為它兼容密鑰派生函數 (KDF) 和密鑰聚合。ElGamal 的非確定性特性（由隨機值k k引入）可確保每次加密操作都生成唯一的密文，從而增強了安全性。

為了降低傳統解密密鑰管理相關的中心化風險（例如在Shamir秘密共享（SSS）方案中，需要在秘密共享之前先確定解密密鑰的存在），我們採用了分佈式密鑰生成（DKG）方法。它提供了一種由每個參與者以去中心化的方式生成解密密鑰的機制，確保任何一方在密鑰公開之前都無法掌握完整的密鑰。

大多數 DKG 協議通過採用可驗證秘密共享 (VSS) 來消除對可信方的需求，VSS 要求參與者交互以驗證共享的有效性。此過程被替換為在投票時按需驗證解密密鑰共享的零知識證明。

雖然 DKG 消除了各方之間密鑰共享交換的需要，但它仍然需要在提案創建期間發佈加密密鑰共享。使用確定性 KDF，參與者可以避免交互過程，從而使提案創建者能夠異步且獨立地聚合最終的加密密鑰。

4. 安全考慮和限制

該協議固有的一些安全風險和限制需要考慮：

  • 可信設置。如果使用 Groth16 作為 zk-SNARK 證明系統，則需要對每個電路進行可信設置，並且必須正確執行。

  • 私鑰/簽名洩露。確保密鑰派生 ECDSA 簽名的私密性至關重要。babyJubJub 密鑰對直接由該簽名派生而來，因此簽名洩露會導致用戶所在的多重簽名系統容易受到網絡釣魚/垃圾郵件攻擊。

  • 提案搶先交易。即使提案挑戰已根據提案內容確定性地得出，仍然有可能利用相同的提案搶先創建提案。這不會直接影響安全性，但應予以注意。

  • 參與者移除僵局。如果被移除的參與者沒有投票（這對他們來說很正常），移除提案將失效，而該參與者仍為多重簽名成員。一個可能的解決方案是對此類提案進行公開投票。

  • 修改參與者列表。每當有活躍（正在進行）的提案時，在多重簽名中添加或刪除參與者會非常困難。這樣做可能會導致加密方案中使用的密鑰不一致。一個可能的解決方案是跟蹤此類提案，並僅在沒有其他正在進行的提案時才允許創建它們。

  • 最後投票者的優勢。由於一旦知道所有解密密鑰份額，就可以解密選票，因此最後一位參與者可以在投票之前重建之前的選票。

  • 可擴展性。投票披露和提案結果計算的複雜性與參與者數量成線性關係。

參考

[1] Nicolas T. Courtois 和 Rebekah Mercer. 隱身地址和密鑰管理技術
區塊鏈系統。2017 年。網址： https://www.scitepress.org/papers/2017/62700/62700.pdf 。
[2] Neal Koblitz. 橢圓曲線密碼系統. 1987. url: https://www.ams.org/journals/mcom/1987-48-177/S0025-5718-1987-0866109-5/S0025-5718-1987-0866109-5.pdf .


相关赛道:
智能合約公鏈
衍生品
Layer 2
來源
免責聲明：以上內容僅為作者觀點，不代表Followin的任何立場，不構成與Followin相關的任何投資建議。
喜歡
收藏
評論
相關推薦