感謝@aelowsson 的審閱和反饋。
本分析的目標是瞭解在增加區塊 gas 限制的情況下,以太坊狀態(每個完整節點的數據庫大小)如何演變,以及重新定價(改變狀態字節和突發資源的有效 gas 成本)如何影響狀態增長和突發吞吐量。
為了實現這一目標,我們:
- 在三種天然氣限制軌跡(基準、激進、保守)下規劃國家規模。
- 構建並校準一個簡單的等彈性需求模型,用於描述狀態創建和突發資源消耗。
- 使用該模型計算新的 EIP-1559 均衡基本費用以及當添加狀態的 gas 限制和/或 gas 價格發生變化時產生的每個區塊資源份額。
- 報告不同價格彈性範圍內的狀態需求和突發需求情景對比。
TLDR
- 如果吞吐量增加,而狀態創建成本保持相對低廉,則狀態規模可以大幅增長。到 2027 年年中,保守方案的總狀態規模將達到 686 GiB,基礎方案為 859 GiB,而激進方案則為 1.08 TiB。所有這些數值都超過了bloatnet 計劃確定的 650 GiB 的關鍵閾值。
- 我們需要就以太坊在中長期內可接受的狀態增長水平達成一致。
- 提高狀態創建的 gas 成本會降低所探索的彈性機制下的預期狀態增長,但會略微降低突發資源吞吐量。
- 吞吐量損失受突發需求彈性的影響比狀態創建成本的影響更大。當突發需求具有價格彈性時,容量翻倍仍然能帶來接近線性的吞吐量提升,重新定價的影響很小。
- 如果狀態創建需求缺乏彈性,那麼提高狀態創建成本預計會導致基礎費用高於狀態不重新定價的情況。如果這種需求富有彈性,則這種效應會逆轉。
1. 我們為什麼關心州的發展?
截至 2025 年 5 月,專用於狀態的 Geth 節點中當前未壓縮的數據庫大小約為 340 GiB。在將 gas 限制從 3000 萬 gas 單位增加到 3600 萬 gas 單位後,每天創建的新狀態的中位數大小翻了一番,從約 102 MiB 增加到約 205 MiB。
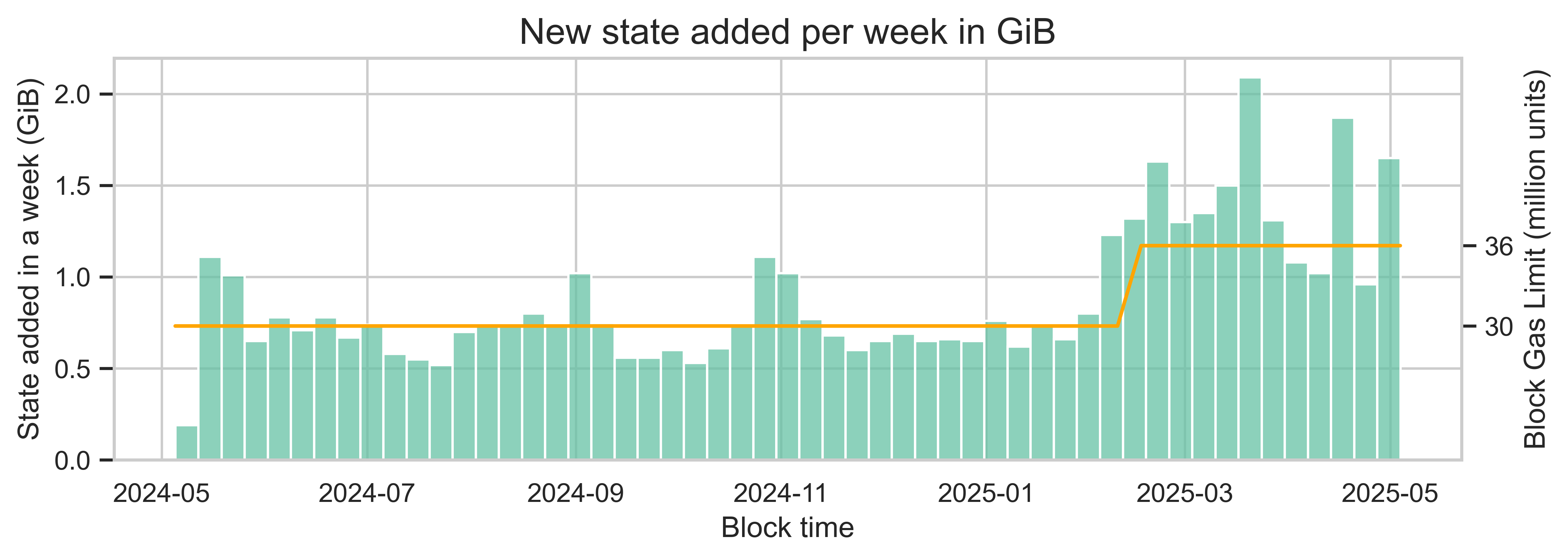
在這個例子中,我們看到的關係並非線性,與預期不符。這可能是由於其他因素影響了用戶行為。然而,在其他條件相同的情況下,我們預期隨著 gas 限制的增加,新創建的狀態數量也會成比例增加。
高州增長率會產生兩個負面的後續影響:
- 如果狀態增長速度超過磁盤改進和每字節存儲容量的減少速度,我們最終會達到這樣一個臨界點:驗證器價格過高,無法滿足運行以太坊驗證器節點所需的磁盤需求。
- 狀態訪問操作(例如
SSTORE的性能很大程度上取決於狀態的大小,狀態越大,這些操作的執行時間就越長。bloatnet項目發現,當狀態大小達到 650 GiB 時,狀態訪問模式會出現關鍵瓶頸,導致狀態訪問時間增加 40%,內存消耗呈指數級增長,同步時間也更長。
目前尚不清楚硬件改進和客戶端優化將如何影響這些瓶頸;然而,鑑於當前對可擴展性的關注以及預期中 gas 上限的提高,我們需要更仔細地研究這個問題。最重要的是,我們需要就以太坊在中長期內可接受的狀態增長水平達成共識。
然而,本報告的重點略有不同:天然氣限額預計將如何影響各州的增長,以及天然氣重新定價將如何改變其增長軌跡。這一點與即將推出的格拉姆斯登(Glamsterdam)分叉方案提出的EIP-8037尤為相關。
2. 區塊限制增加時,州的發展情景:州可以發展到多大?
為了回答這個問題,我們設計了從 2025 年 5 月 1 日到 2027 年年中期間三種不同的天然氣限量增加方案:
| 日期 | 保守的 | 根據 | 挑釁的 |
|---|---|---|---|
| 2025-05-01 | 36 | 36 | 36 |
| 2025-07-01 | 45 | 45 | 45 |
| 2025-12-01 | 60 | 60 | 60 |
| 2026-06-01 | 80 | 100 | 150 |
| 2026-12-01 | 150 | 300 | 500 |
| 2027-06-01 | 200 | 400 | 700 |
然後,對於每個調度,我們計算相應的狀態增長率,假設每天的狀態增長量與 gas 限制成正比,並且基準測量的狀態創建率為在 36M gas 限制下每天 205 MiB:
new_state_per_day = 205 MiB * (G / 36M)
由此,我們可以得出每次天然氣限價調整日各州每日增長率如下:
| 日期 | 保守估計(百萬字節/天) | 基礎(MiB/天) | 激進型(MiB/天) |
|---|---|---|---|
| 2025-05-01 | 205 | 205 | 205 |
| 2025-07-01 | 256 | 256 | 256 |
| 2025-12-01 | 342 | 342 | 342 |
| 2026-06-01 | 456 | 569 | 854 |
| 2026-12-01 | 854 | 1708 | 2847 |
| 2027-06-01 | 1139 | 2278 | 3986 |
下圖顯示了未來兩年內三種天然氣供應方案的總狀態大小(單位:GiB)。
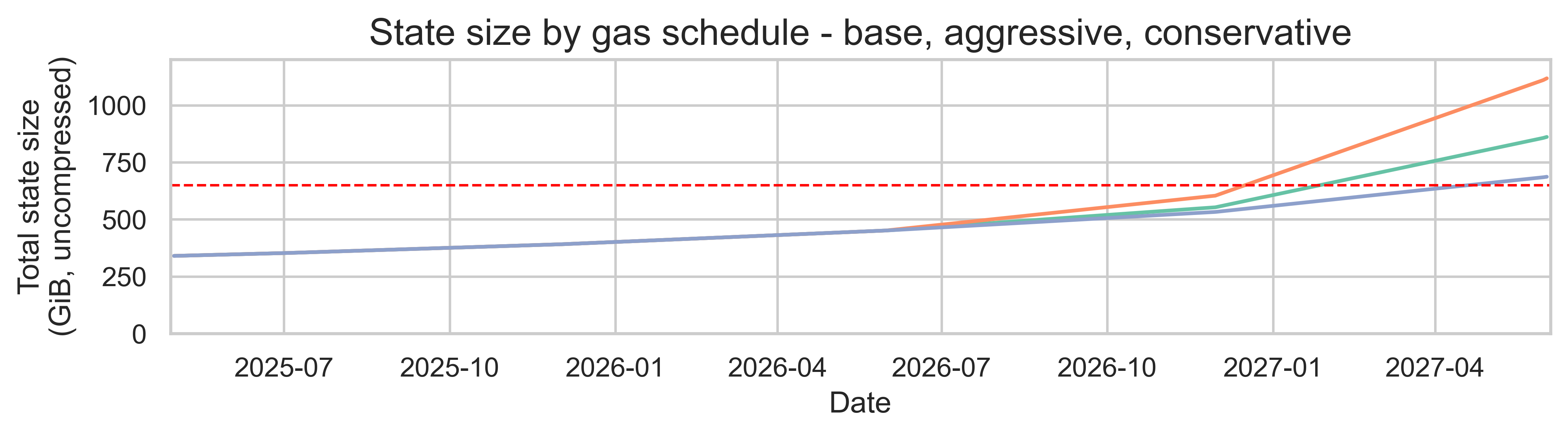
在比例縮放(保持相同 gas 成分)下,增加區塊限制會線性增加每日狀態創建量(因為我們將測得的 205 MiB/天按 gas 限制比例進行縮放)。由於每日新增狀態會累積,因此不同 gas 方案下的總狀態大小會在數月和數年內出現差異。到 2027 年年中,保守方案的總狀態大小將達到 686 GiB,基礎方案為 859 GiB,而激進方案為 1.08 TiB。所有這些值都超過了bloatnet 倡議確定的 650 GiB 臨界閾值。
3. 重新定價如何影響州增長和吞吐量?
既然我們已經確定了在價格不變的情況下狀態增長的潛在情景,我們就可以分析提高狀態創建操作的 Gas 價格如何影響狀態增長和可擴展性。
3.1 模型和推導
我們首先定義一個簡單的模型,該模型允許我們估算平均每日狀態增長量以及區塊中可用於突發操作(計算、狀態訪問和數據)的 gas 量。
模型輸入
- G G :阻塞氣極限。
- b b :以 gwei 為單位的均衡基本費用b b 。
- g_\text{state} g state : 添加到狀態字節的每個新字節的 gas 成本。
- g_\text{burst} g burst :每秒突發資源使用所需的 gas 費用。
- S(p) S ( p ) : 狀態創建的需求曲線,以價格p為單位衡量願意在一個塊中添加的淨狀態字節總數。注意, p是以 gwei 為單位向狀態添加一個字節的成本,計算公式為p=b\cdot g_\text{state} p = b ⋅ g state 。
- B(p) B ( p ) : 需求曲線突發資源使用情況,以價格p p為單位衡量願意在區塊中添加的時隙時間(以秒為單位)。在這種情況下, p=b\cdot g_\text{burst} p = b ⋅ g burst 。
模型假設
- 基本費用遵循 EIP-1559 設計,其中區塊使用量超過G G的 50% 會導致下一個區塊的基本費用增加,而區塊使用量低於G G的 50% 會導致下一個區塊的基本費用減少。
- 按照目前的設計,區塊平均佔用 50% 的Gas ,其中 30% 用於狀態創建,其餘用於突發資源。
- 當 50% 的G G足以滿足狀態創建和突發資源使用的需求,且價格為p p時,即可達到平均塊均衡。
- 兩條需求曲線均採用兩個獨立的等彈性模型進行建模:
這裡,我們假設對可處理性的需求是獨立的等彈性需求。然而,在實踐中,狀態創建和突發資源的需求很可能是相關的:狀態字節有效價格的變化會影響突發秒數的需求(反之亦然)。採用包含交叉價格彈性的聯合多元需求模型可以更好地捕捉資源之間的替代或互補關係,但這會引入額外的參數和識別挑戰。
設想
- 氣體極限增加n倍,即G = n \, G^0 G = n G 0
- 州天然氣成本增加m倍,即g_\text{state} = m \, g_\text{state}^ 0 g state = m g 0狀態
我們預計基本費用會下降,直到達到一個新的平衡狀態,屆時狀態資源和突發資源都會得到充分利用。
基礎推導
設價格為p時,每個區塊的均衡使用量為
- 狀態字節: S(p)=S(b g_\text{state}) S ( p ) = S ( b g state )
- 突發秒數: B(p)=B(b g_\text{burst}) B ( p ) = B ( b g burst )
基準費用 b 中每個區塊所用的天然氣量定義為:
對於該場景,EIP-1559 使b b趨向於值b^* b ∗ ,使得:
在這種新的平衡狀態下,我們得到以下每個區塊的使用情況:
- S^* = S(b^* \, m\, g_\text{state}^0) S ∗ = S ( b ∗米g 0狀態) ,這導致平均每年狀態增長2,628,000\cdot S^* 2,628,000 ⋅ S ∗字節。請注意, 2,628,000 2,628,000是每年的數據塊數(即每 12 秒一個數據塊)。
- B^* = B(b^* g_\text{burst}^0) B ∗ = B ( b ∗ g 0 burst )
每種資源類型的份額如下:
- \text{Share}_\text{state}=\frac{m\,g_\text{state}^0S^*}{0.5\, n\, G_\text{limit}^0} Share state = m g 0狀態S ∗ 0.5 n G 0極限
- \text{Share}_\text{burst}=1-\text{Share}_\text{state}突發份額= 1 −狀態份額
校準
已知當前G=G^0 G = G 0 ,均衡b=b^0 b = b 0 ,初始 gas 價格g_\text{state}^0 g 0 state和g_\text{burst}^0 g 0 burst ,我們得到:
- g_\text{state}^0 S(b^0 g_\text{state}^0)= 0.3 \cdot 0.5 \cdot G^0 = 0.15\, G^0 g 0 state S ( b 0 g 0 state ) = 0.3 ⋅ 0.5 ⋅ G 0 = 0.15 G 0
- g_\text{burst}^0 B(b^0 g_\text{burst}^0)= 0.7 \cdot 0.5 \cdot G^0 = 0.35\, G^0 g 0 burst B ( b 0 g 0 burst ) = 0.7 ⋅ 0.5 ⋅ G 0 = 0.35 G 0
由此,我們可以將A_s和A_b校準如下:
A_s = S(p)p^{\varepsilon_s} = \frac{0.15\,G^0}{g_\text{state}^0}\,(b^0g_\text{state}^0)^{\varepsilon_s} A s = S ( p ) p ε s = 0.15 G 0 g 0狀態( b 0 g 0狀態) ε s
A_b = B(p)p^{\varepsilon_b} = \frac{0.35\,G^0}{g_\text{burst}^0}\,(b^0g_\text{burst}^0)^{\varepsilon_b} A b = B ( p ) p ε b = 0.35 G 0 g 0爆發( b 0 g 0爆發) ε b
在這種選擇下,對於任意b值,我們得到平衡狀態下模塊中所用氣體的以下公式:
我們還可以根據 gas 限制和當前狀態增長率來估算g_\text{burst}^0 g 0 burst 。這裡我們假設 gas 限制利用率為 50%,並取平均成本:
對於突發資源,我們將根據最壞情況的區塊進行定價,即假設如果區塊中充滿了突發資源操作直到達到區塊限制,則執行時間為 2 秒:
由此,我們可以直接推導出突發資源的基本吞吐量:
情景推導
在這種情況下, G=n\,G^0 G = n G 0 , g_\text{state}=m\,g_\text{state}^0 g state = m g 0狀態和g_\text{burst}=g_\text{burst}^0 g burst = g 0 burst ,這使得平衡狀態下模塊中使用的氣體總量為:
此外,在平衡狀態下,我們使用了新氣體極限的 50%,因此:
我們可以計算該多項式的根來找到均衡基本費用b^* b ∗ 。如果該多項式存在根r \in \mathopen] 0,1\mathclose[ r ∈ ] 0 , 1 [ ,則b^* = b^0 \, r b ∗ = b 0 r .由此,我們可以計算出基本推導中定義的每個區塊的使用量和 gas 份額。
以下各節將探討三種情景的影響:
- 基準(不重新定價): n=2 n = 2 (雙倍 gas 限制), m=1 m = 1 (狀態 gas 成本不變)
- 雙州汽油價格: n=2,m=2 n = 2 , m = 2
- 三態天然氣價格: n=2,m=3 n = 2 , m = 3
在所有情況下,我們都假設氣體極限加倍( n=2 n = 2 )。
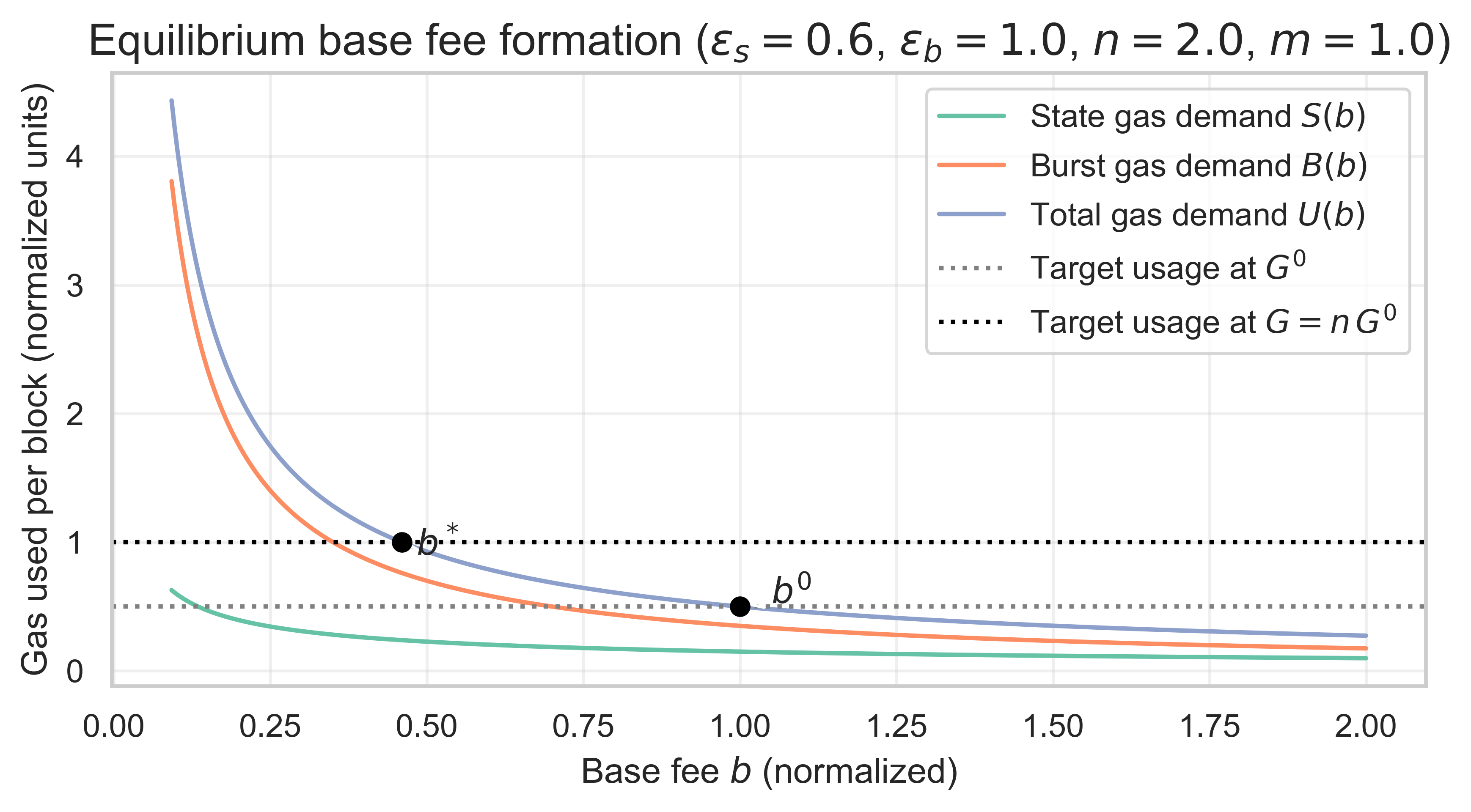
對於每種情景,我們掃描網格(0.1 到 1.5)上的 ε <sub> s </sub>和ε<sub> b </sub> ,並求解b<sup>* </sup> 。利用均衡基準費用b<sup>* </sup> ,我們計算S<sup>* </sup> 、 B<sup>* </sup> 、年度州增長率(單位為 GiB)以及資源天然氣份額。為了便於理解,下圖展示了基準情景下的新均衡,假設ε<sub> s </sub> = 0.6和ε<sub> b </sub> = 1。
3.2 重新定價對國家創建天然氣使用份額的影響
以下圖表顯示了所有價格彈性組合(\varepsilon_s, \varepsilon_b)下,狀態創建操作在均衡塊中使用的氣體份額( ε s , ε b ) 。
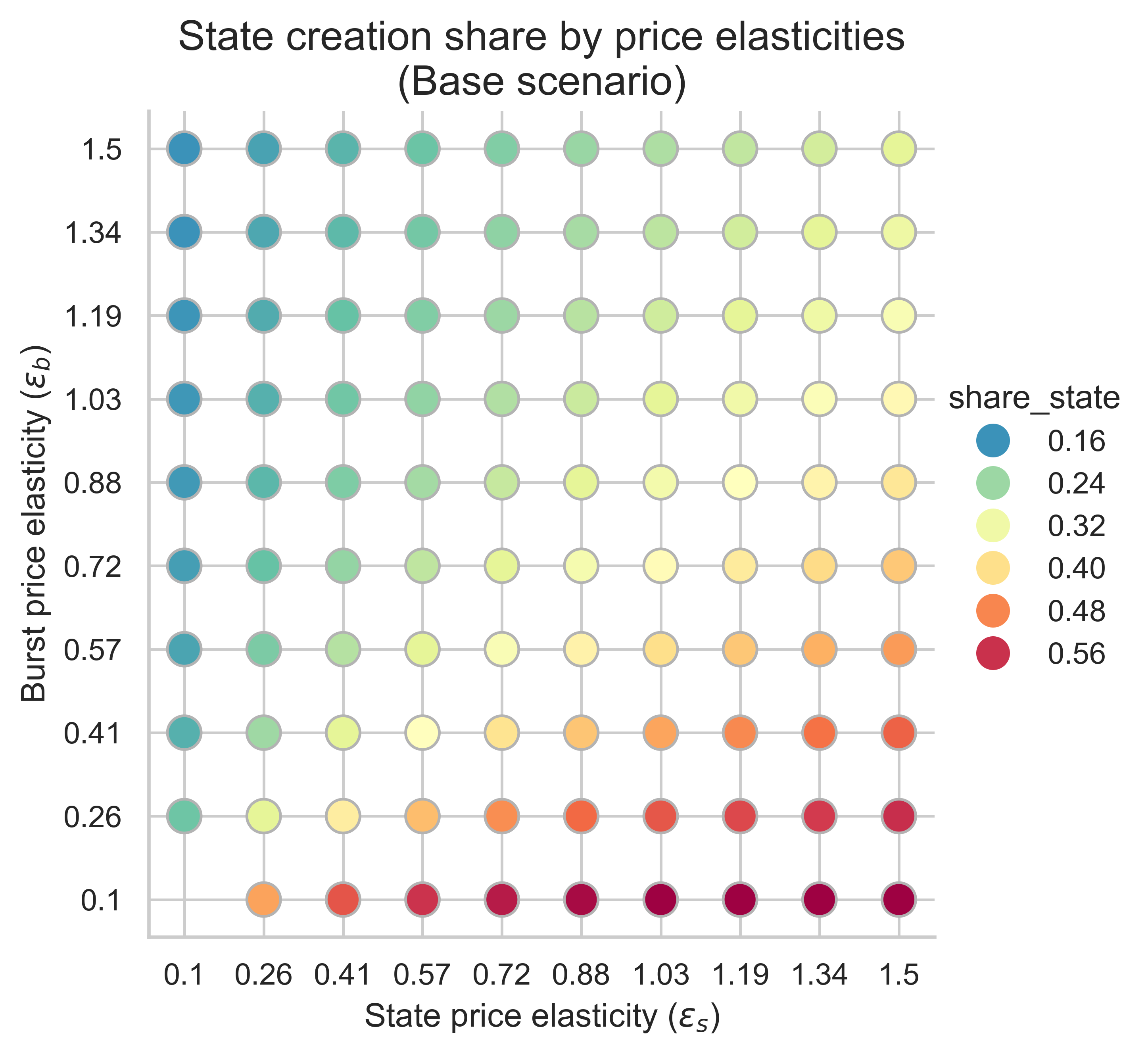
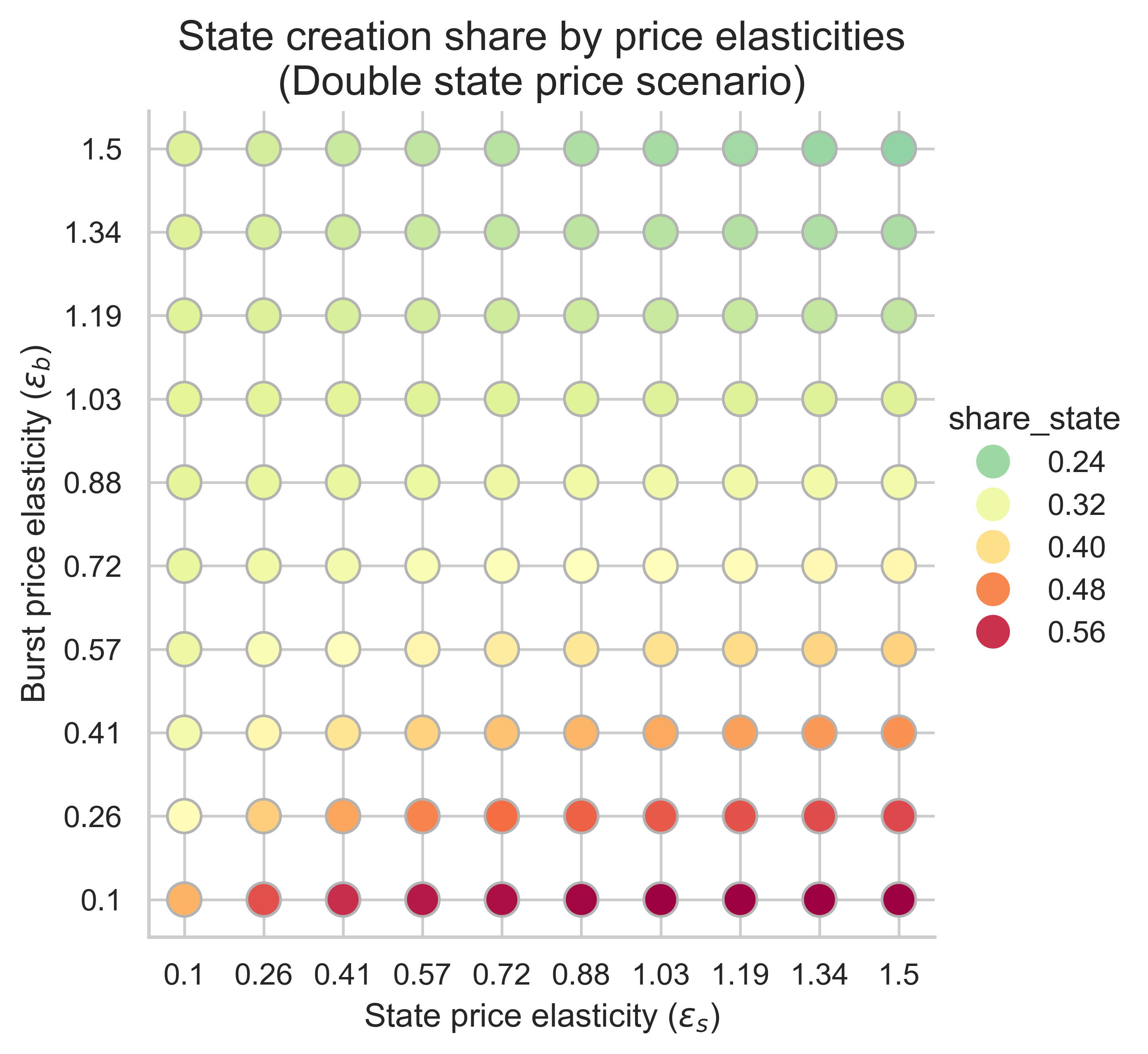
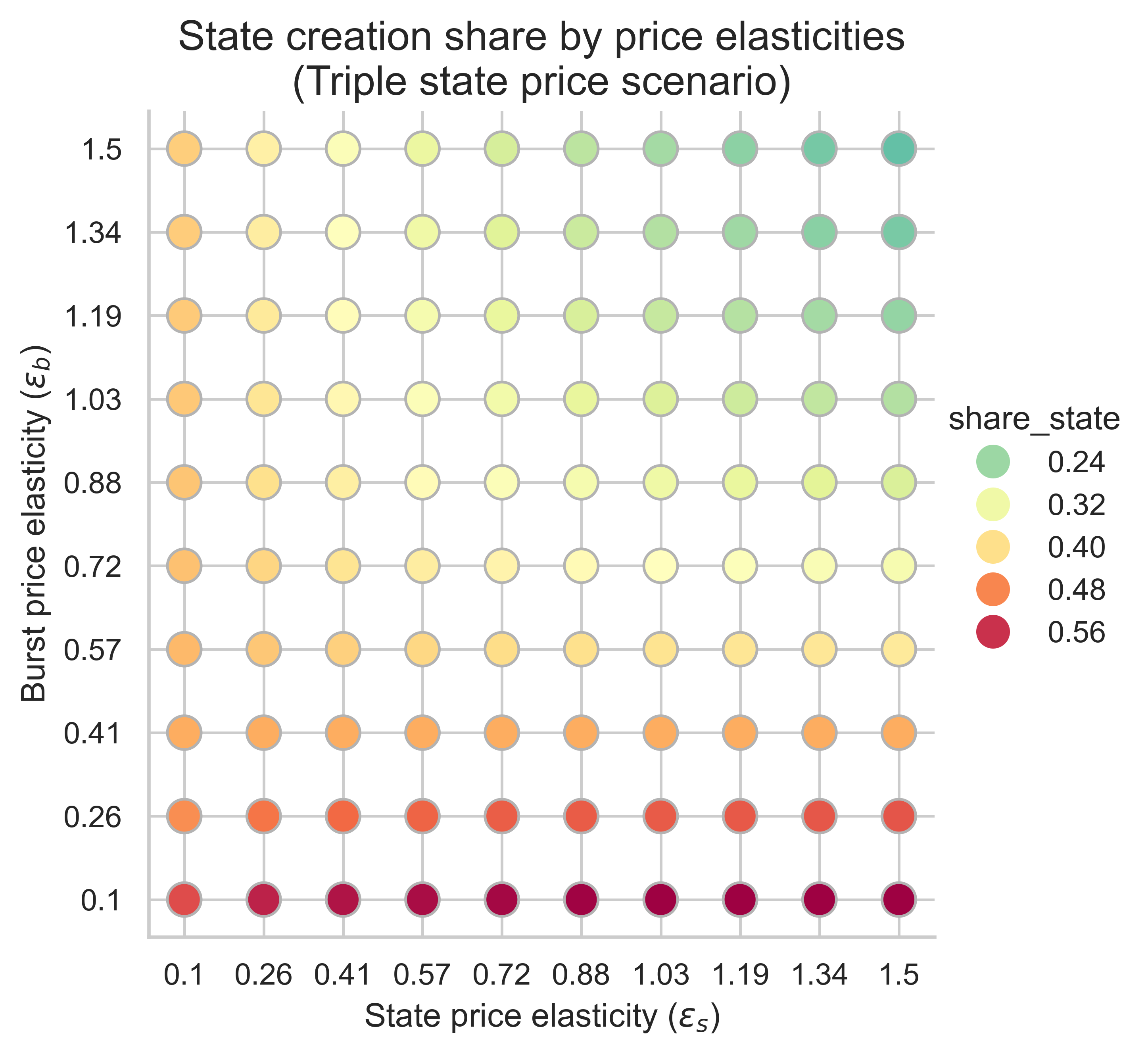
當m = 1 (不重新定價)且n = 2 (雙倍gas上限)時,狀態創建消耗的區塊 gas 比例相對於當前的 30% 有所增加,因為狀態創建的需求彈性大於突發資源的需求彈性。因此,如果狀態創建對價格變化的適應性強於對突發資源使用量的適應性,那麼提高 gas 上限可能會導致更多區塊容量用於狀態創建,因為更多的狀態創建需求會湧入區塊以利用更低的基礎費用。
增加m m (使狀態創建成本更高)會影響狀態低彈性機制和突發資源高彈性機制中用於狀態創建的區塊份額:
- 當狀態創建的需求彈性較低時(圖表的左側),我們看到用於狀態創建操作的 gas 比例較高, m m越大,比例就越高。
- 相反,當兩個需求都具有高彈性時(右上角),效果則相反,與m= 1的情況相比,用於狀態創建的模塊比例會減少。變化的幅度同樣取決於m 。
- 狀態創建比例最高的情況出現在突發資源需求彈性較低的時候(圖的下半部分)。在這種情況下,增加狀態創建成本不會產生任何影響。
總之,提高狀態創建的 gas 成本可能會對均衡區塊中用於狀態創建的份額產生正面或負面的影響。這取決於彈性機制。然而,當基準情景下用於狀態創建的區塊空間份額已經很高時( m=1 ) ,提高狀態創建的 gas 成本並不會顯著影響這一份額。換句話說,如果我們處於一種彈性機制下,隨著區塊限制的增加,用於狀態創建的 gas 份額已經很高,那麼提高其 gas 價格不會產生顯著影響。
3.3 重新定價對年度州增長的影響
以下圖表顯示了所有價格彈性組合(\varepsilon_s, \varepsilon_b)的年度州增長率( ε (s , ε( b) ) 。這裡我們假設平均塊是均衡塊。該指標對於理解提高狀態創建操作成本在緩解狀態增長方面的有效性至關重要。
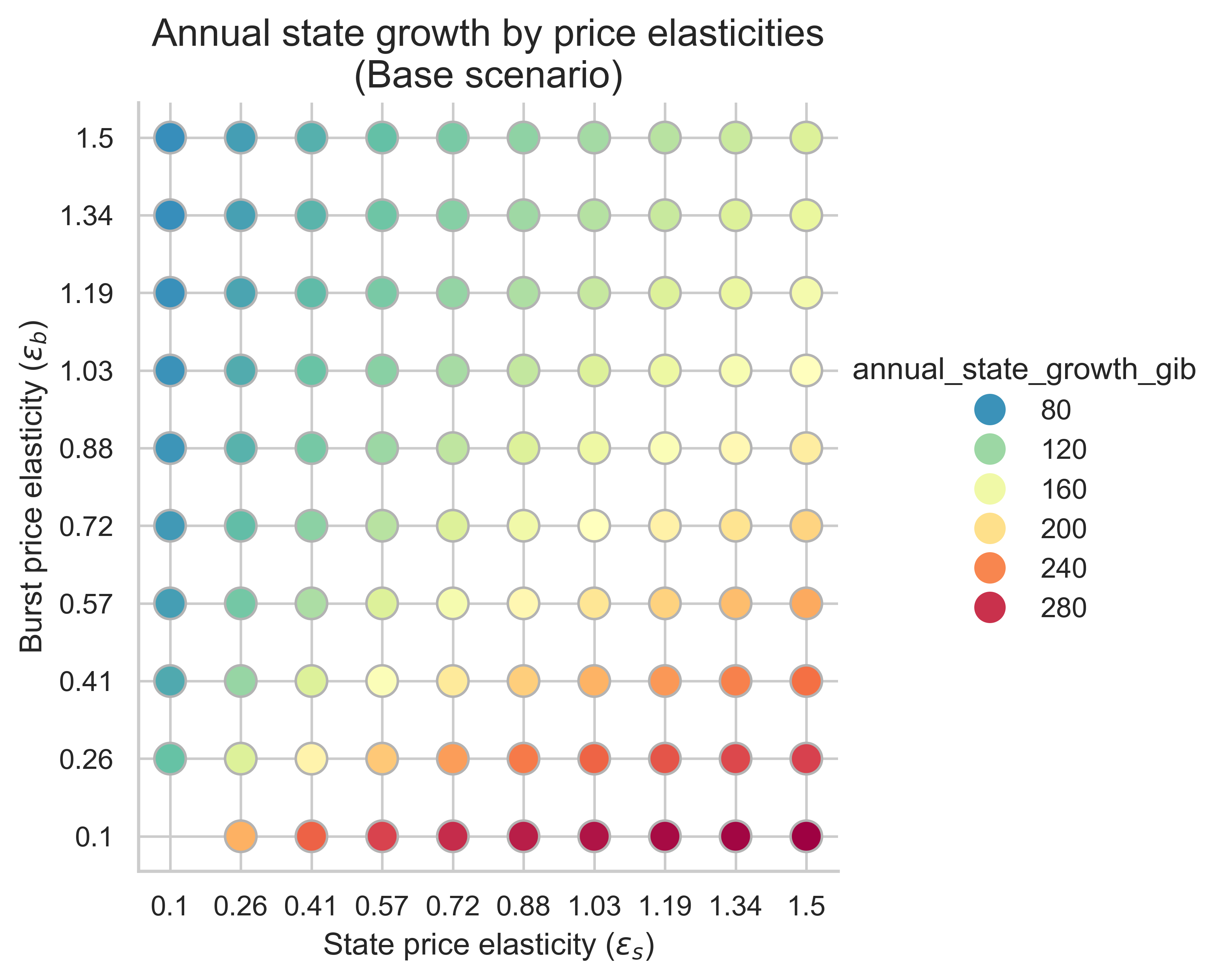
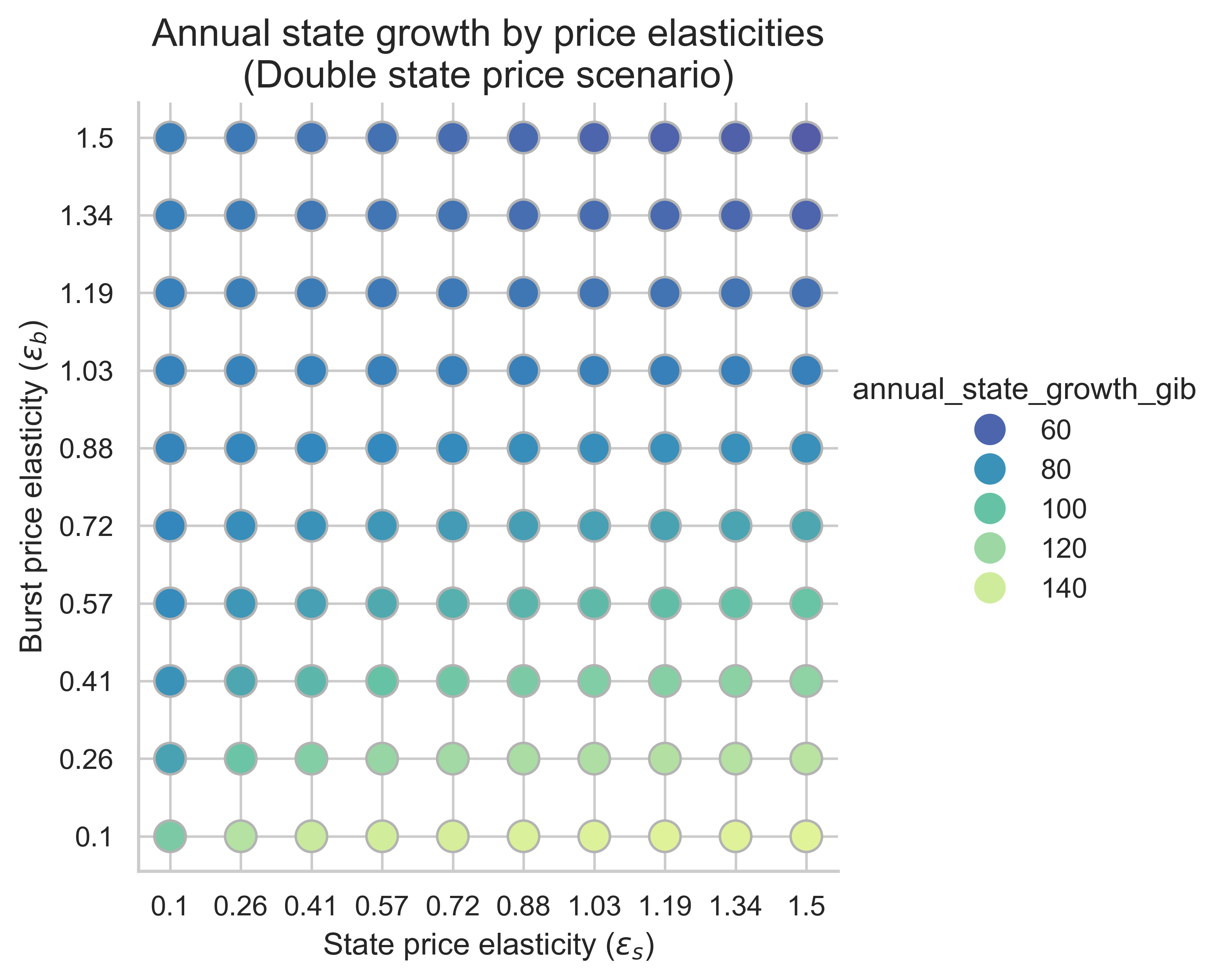
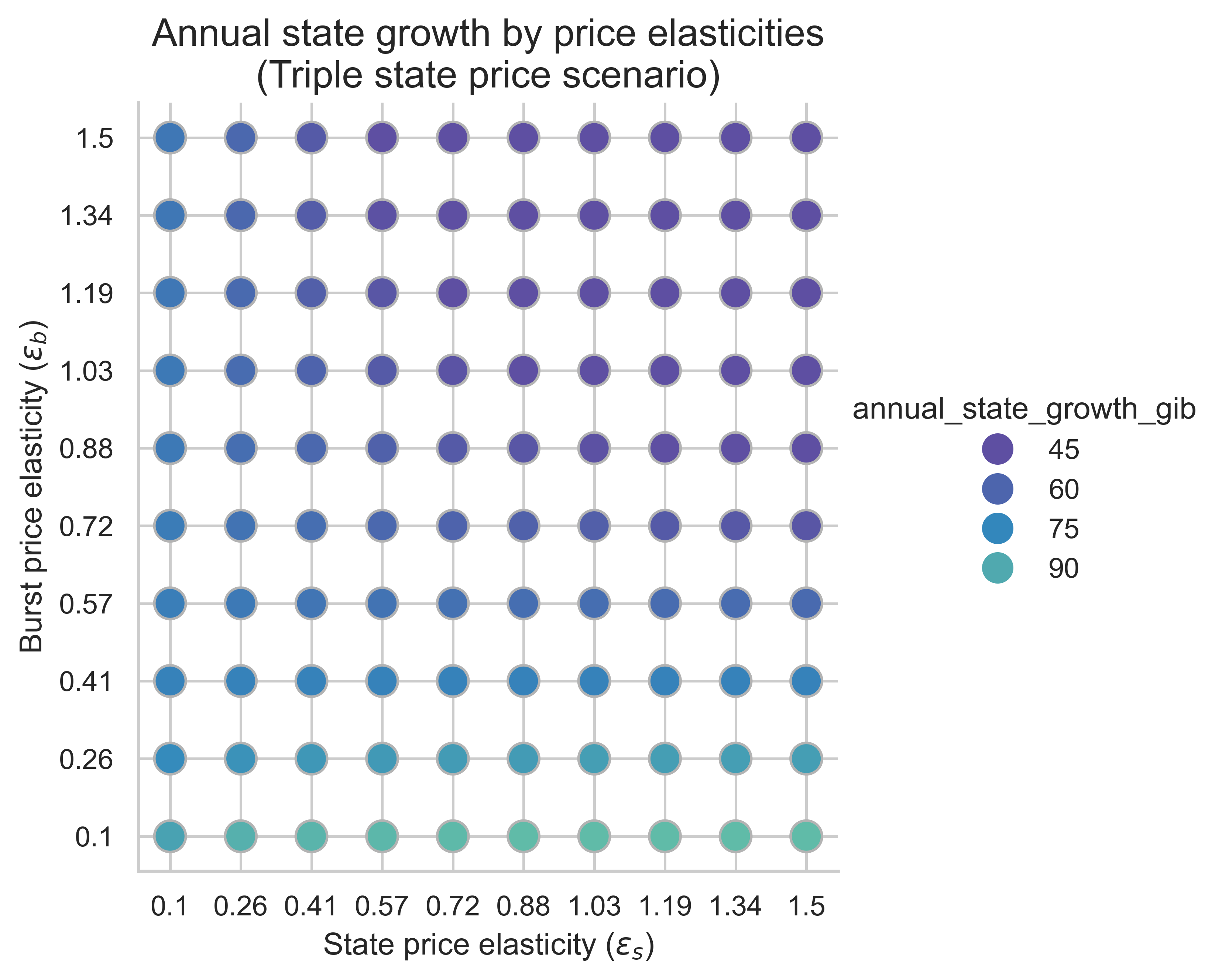
不出所料,與不重新定價的情況相比,提高狀態創建操作的成本會降低所有彈性範圍內的狀態增長率。這表明,提高狀態創建的 Gas 成本能夠有效抑制各種價格彈性下的狀態增長。
增加狀態創建的 Gas 成本會產生另一個有趣的效應。我們可以通過繪製每個場景下年度狀態增長率與狀態需求彈性\varepsilon_s ε s的關係圖來觀察這一點。每個箱線圖的變化是由於突發需求彈性\varepsilon_b ε b造成的。
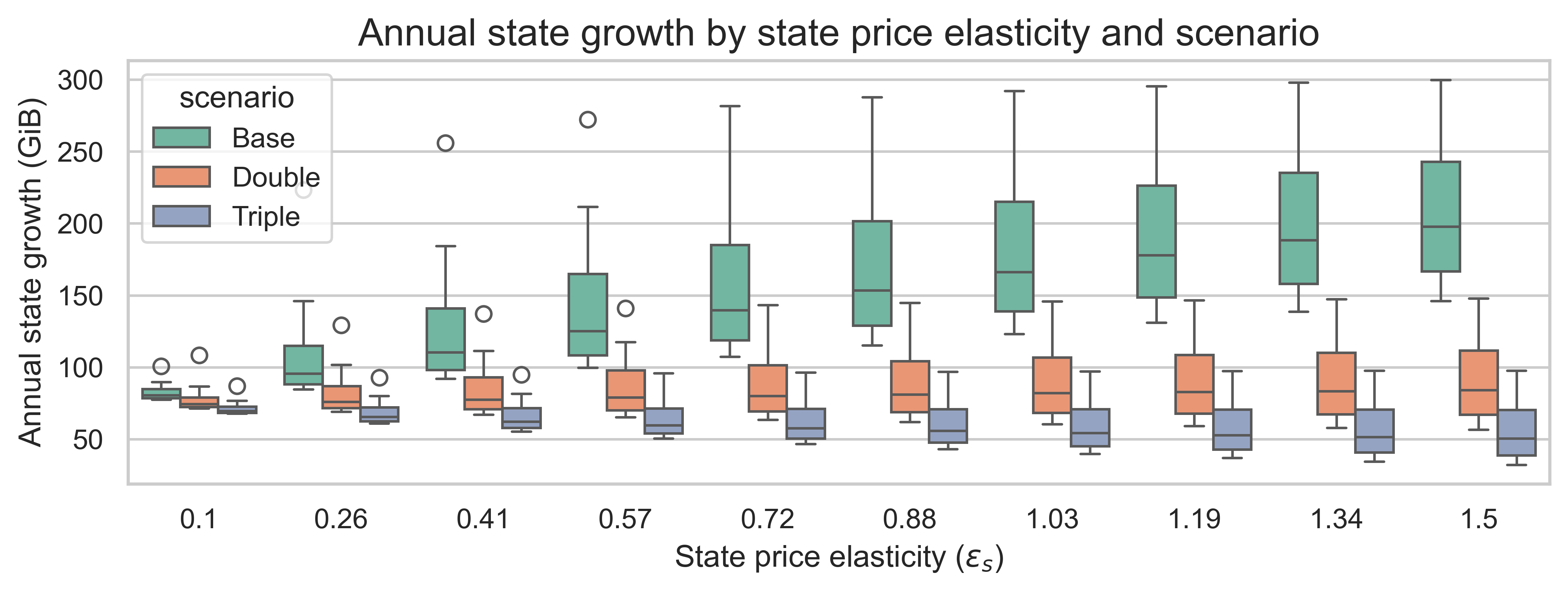
- 無需重新定價:較高的\varepsilon_s \implies ε s ⟹更多州增長
- 重新定價等於區塊限制的增加量:更高的\varepsilon_s \implies ε s ⟹州中位數增長率沒有變化
- 重新定價高於區塊限制的增幅:更高的\varepsilon_s \implies ε s ⟹州增長減少
我們應該注意到,突發資源的需求彈性也會影響狀態增長:彈性越低,所有場景下的狀態增長率就越高。
3.4 重新定價對突發資源吞吐量的影響
以下圖表顯示了均衡塊中所有價格彈性組合(\varepsilon_s, \varepsilon_b)下突發資源的吞吐量增益( ε s , ε b ) 。增益是在 0.7 秒基準吞吐量的基礎上計算的。
該指標對於衡量狀態創建成本增加對可擴展性的影響至關重要。如果我們把可用 gas 翻倍,突發資源的吞吐量是否還能至少翻倍?請記住,基準吞吐量為 0.7 秒。
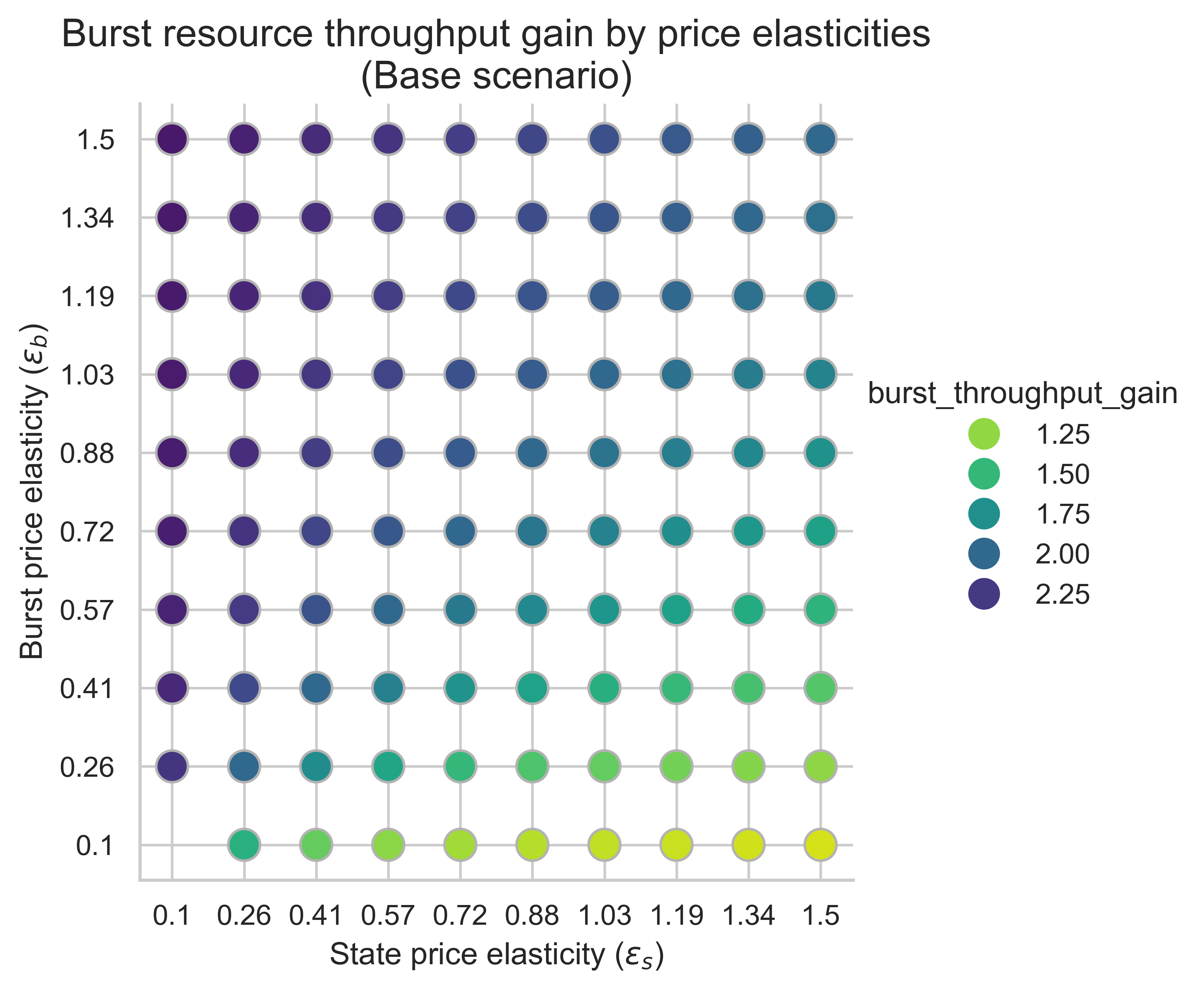
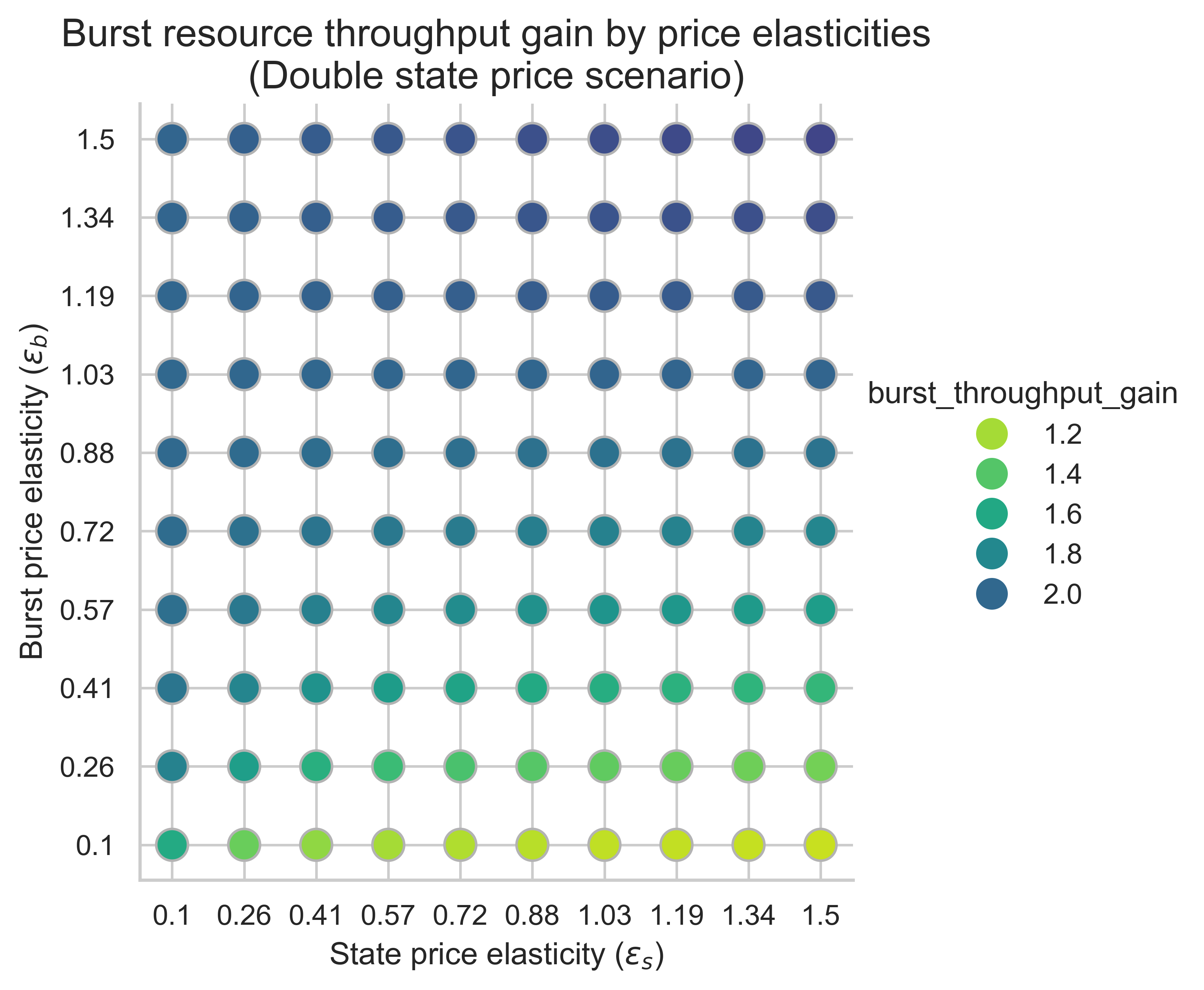
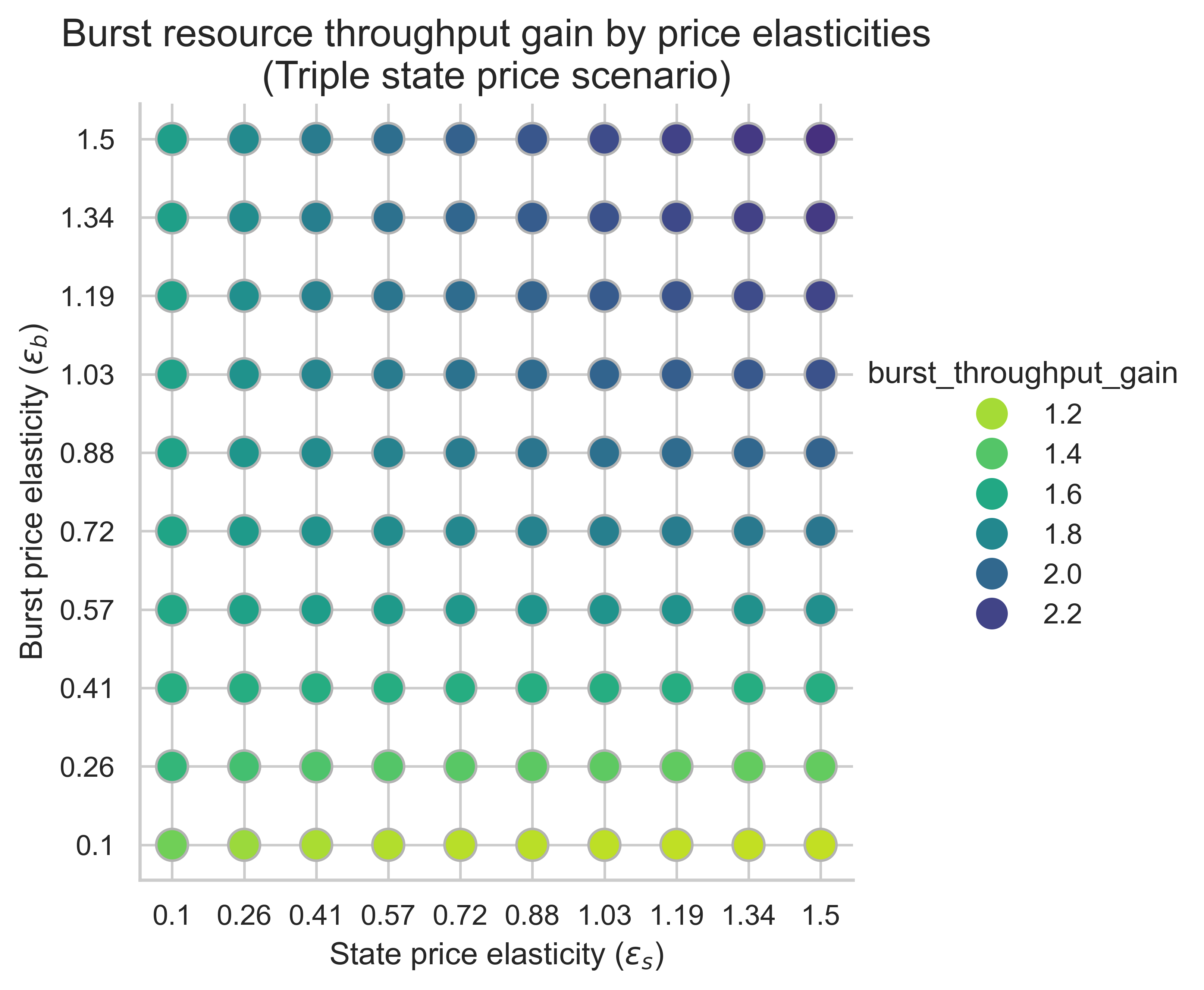
在所有三種情況下,突發吞吐量提升的主要驅動因素是突發側價格彈性\varepsilon_b ε b 。隨著\varepsilon_b ε b 的增加,我們看到相對於 0.7 秒基準線,增益越來越大:
- 當突發需求具有足夠的價格彈性(圖表的上半部分)時,產能翻倍意味著突發吞吐量翻倍(或略微增加)。
- 當突發需求缺乏彈性時(圖表底部),產能翻倍所對應的突發吞吐量不到翻倍。
相比之下,水平方向隨狀態彈性ε<sub> s </sub>的變化更為複雜。當m = 1 時,隨著ε <sub> s </sub>增大,增益略有下降。而當m = 2或m = 3時,突發資源吞吐量增益在兩個價格彈性都較高時達到最高。
在下圖中,我們可以更清楚地看到提高狀態創建成本對吞吐量的影響。每個箱線圖的變化是由於狀態需求彈性\varepsilon_s ε s引起的。
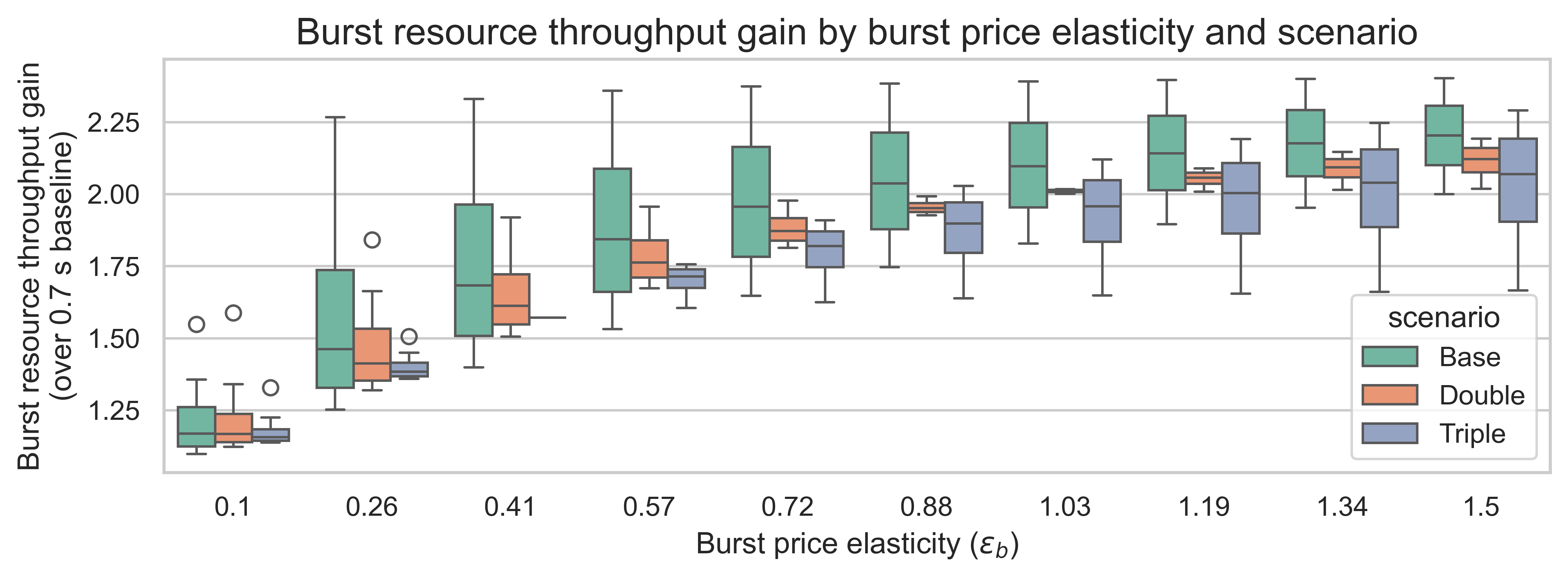
一般來說,成本上升會略微降低吞吐量的提升。然而,與突發資源需求彈性的影響相比,這種影響微乎其微。如果處於高ε<sub> b</sub> ε <sub> b </sub>狀態,那麼增加狀態創建對吞吐量的影響小於25%。
3.5 均衡費用
我們要分析的最後一個指標是均衡基本費用。我們預期該費用會低於基準值b^0=1 b 0 = 1。然而,在不同的彈性機制和重新定價的情況下,費用會降低多少呢?下圖展示了三種重新定價情景下的均衡基本費用以及突發需求彈性。每個箱線圖的變化是由狀態需求彈性\varepsilon_s ε s引起的。
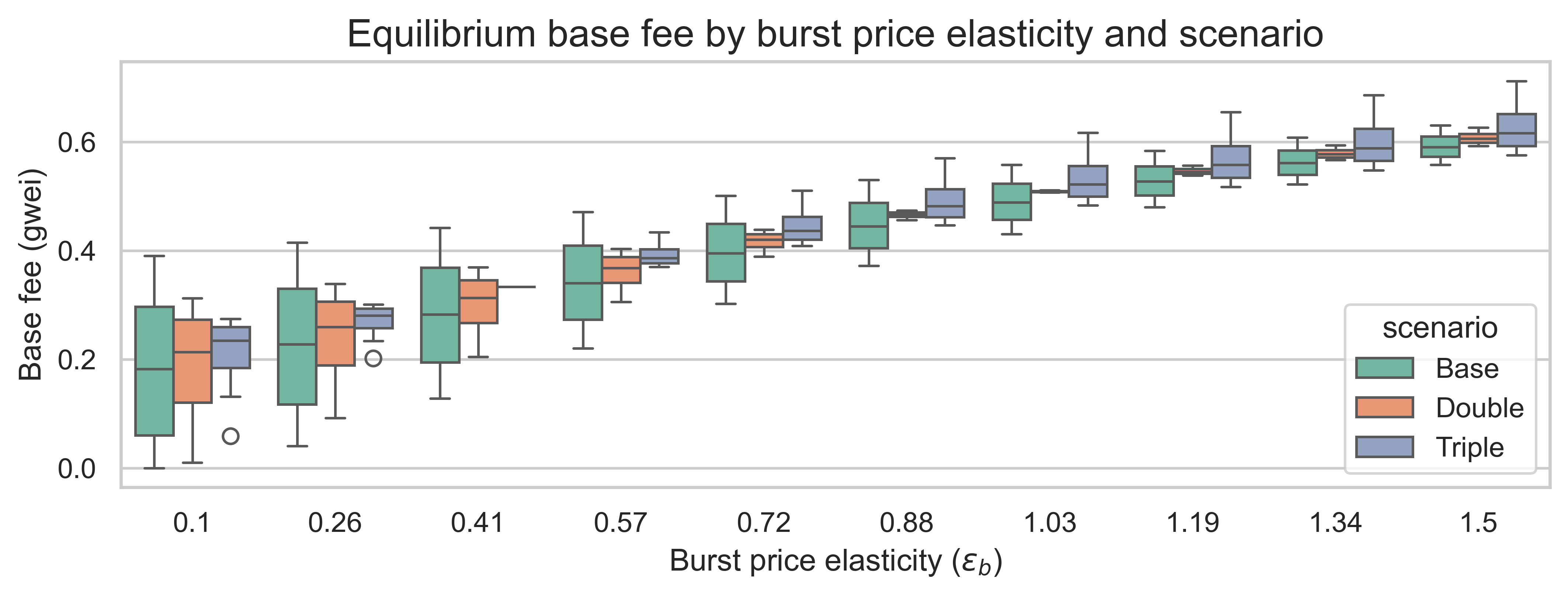
在所有三種定價情景下,均衡基礎費用均隨突發需求價格彈性的增加而增加:從突發需求彈性很低( ε<sub> b </sub> ≈0.1 )到彈性很高( ε<sub> b </sub> ≈1.5 ) ,基礎費用的中位數大約會增加兩倍。當彈性較高時,會有更多需求來填充可用燃料,從而導致更高的基礎費用。
那麼狀態需求彈性如何呢?下圖顯示了三種重新定價方案的均衡基本費用和狀態需求彈性。每個箱線圖的變化是由於突發需求彈性\varepsilon_b ε b造成的。
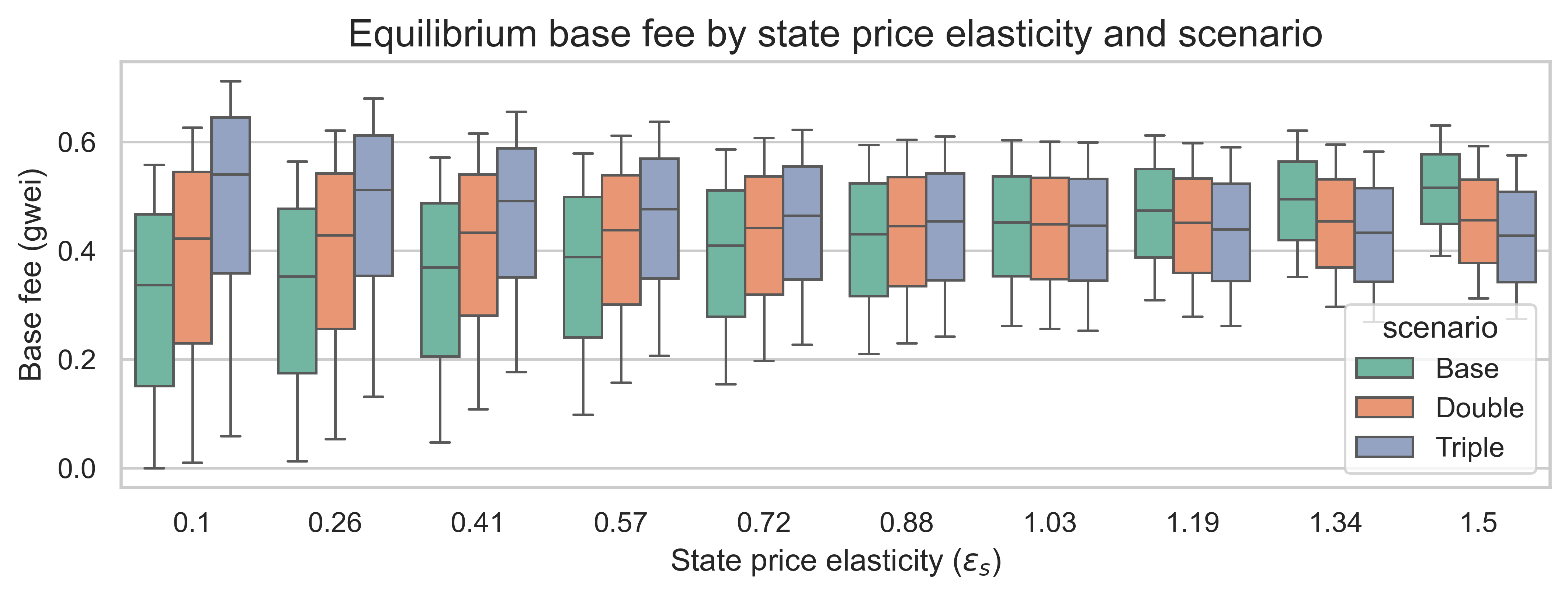
有趣的是,我們並未觀察到基本費用與各州需求之間存在同樣的線性關係,基本費用的中位數似乎不受各州需求彈性的影響,始終保持在相似的範圍內。然而,彈性機制確實會對不同情景下的排序產生影響:
- 當州需求缺乏彈性時(圖表左側),較高的州價格會導致更高的均衡費用。在這種情況下,提高州的價格對需求的影響不大,因此,相同的州需求需要消耗更多的天然氣。
- 當狀態需求彈性較大時(圖表右側),較高的狀態價格會導致較低的均衡費用。在這種情況下,狀態創建需求對狀態成本的增加反應更為強烈,從而降低了基本費用。
4. 討論和後續步驟
首先,在我們簡化的模型下,提高狀態創建操作的成本可以有效抑制所有價格彈性下的狀態增長。因為gas不足以支撐狀態像基礎定價方案下那樣大幅增長。然而,這仍然會導致突發資源吞吐量略微下降。突發資源的需求彈性會加劇這種影響——需求彈性越大,所有定價方案下的吞吐量提升就越高。如果狀態創建需求缺乏彈性,那麼提高狀態創建成本預計會導致基礎費用高於狀態不重新定價的情況。
一個自然而然的問題是,實際系統在(ε<sub>s</sub>, ε<sub>b</sub>) ( ε <sub>s</sub> , ε<sub> b </sub> )網格中的位置。我們的初步實證分析表明,短期內狀態創建的需求彈性適中:以美元計價的基礎費用上漲 1%,在接下來的幾天裡,每單位 gas 創建的新狀態數量僅下降約 0.6%。從等彈性角度來看,這表明短期內狀態創建的總工作負載約為 ε<sub> s </sub> ≈ 0.6 。這與直覺相符,即許多狀態密集型操作(例如開倉、創建合約、鑄造代幣、將數據提交到 Rollup 等)是由持續時間更長的經濟決策和協議級策略驅動的,這些決策和策略不會立即根據價格變化進行調整。我們還應該補充一點,像 XEN 這樣的垃圾合約預計會造成價格下限,因為每當狀態創建的總成本低於某個閾值時,機器人就會用大量狀態交易淹沒網絡,從而增加未來區塊的基本費用。
對於突發資源,我們目前還沒有可比的估計,但有理由預期其彈性會更高,至少在大部分工作負載中是如此。許多以突發為主的活動(套利、清算、MEV 搜索、對延遲敏感的交易)都受到明確的費用限制,並且可以迅速減少。








