作者:David Wong
來源:https://www.cryptologie.net/posts/hash-based-signatures-part-i-one-time-signatures-ots/
Lamport 簽名
1979 年 10 月 18 日,Leslie Lamport 出版了他發明的一次性簽名。
絕大部分簽名方案的安全證明都部分依賴於單向函數(one-way functions),一般來說是哈希函數。而 Lamport 方案的優雅之處在於,這種簽名僅僅依賴於這些這些單向函數的安全性。
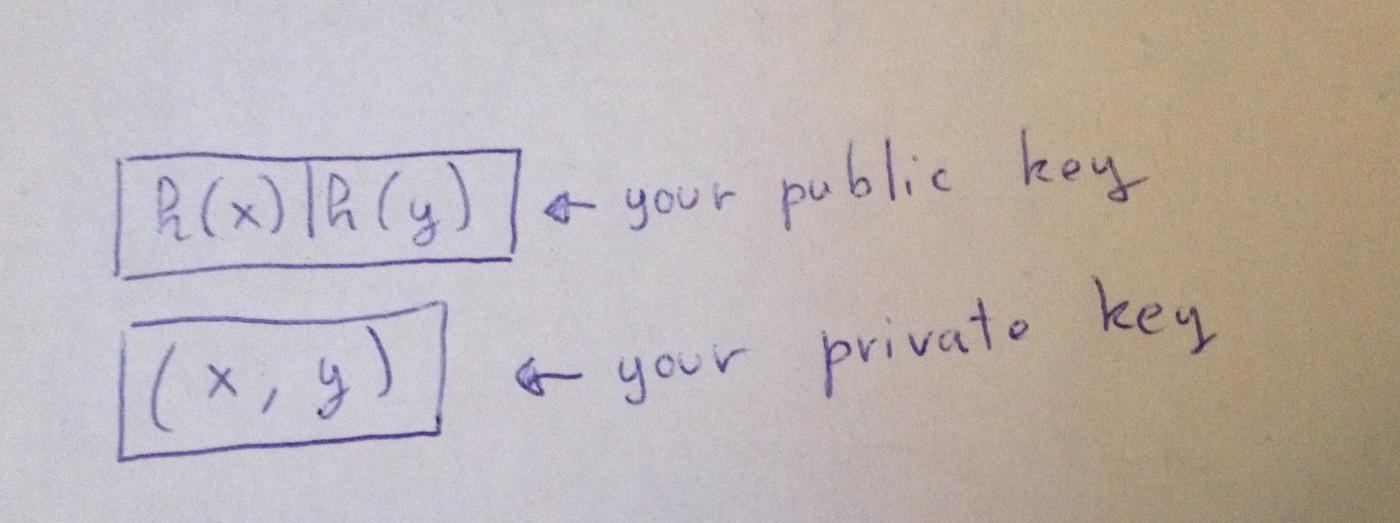
(H(x) | H(y)) <-- 你的公鑰(x, y) <-- 你的私鑰Lamport 是一種非常簡單的方案,首先 x 和 y 都是整數,要簽名一個比特的時候:
- 如果這個比特的值是
0,那就發佈x - 如果這個比特的值是
1,那就發佈y
非常簡單對吧?但顯然,你不能用同一個公鑰重複簽名。
那麼,如果要簽名多個比特的話,該怎麼辦呢?你可以先把自己要簽名的消息哈希一下,比如放到 SHA-256 哈希函數里面(其輸出的長度是可以預測的,從而,固定下要簽名的東西的長度)。
現在,(要簽名 256 個比特),你需要 256 個私鑰對:
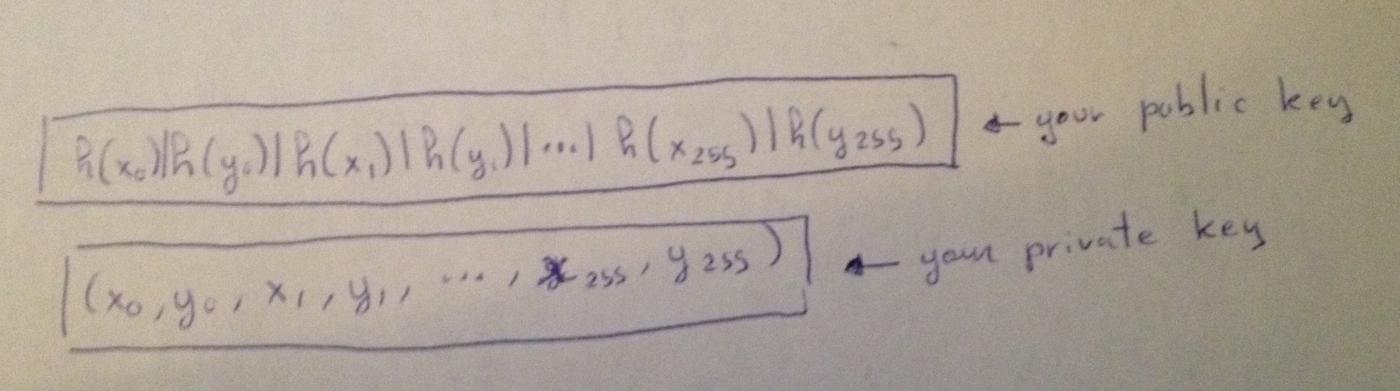
(H(x_0) | H(y_0) | H(x_1) | H(y_1) | ... | H(x_255) | H(y_255)) <-- 你的公鑰(x_0, y_0, x_1, y_1, ... x_255, y_255) <-- 你的私鑰舉個例子,如果你要簽名 100110,那麼你需要發佈 (y_0, x_1, x_2, y_3, y_4, x_5)。
Winternitz OTS(WOTS)
Lamport 的論文出版的幾個月後,斯坦福大學數學系的 Robert Winternitz 提出,可以公開 $h^w(x)$ 而非 $h(x) | h(y)$
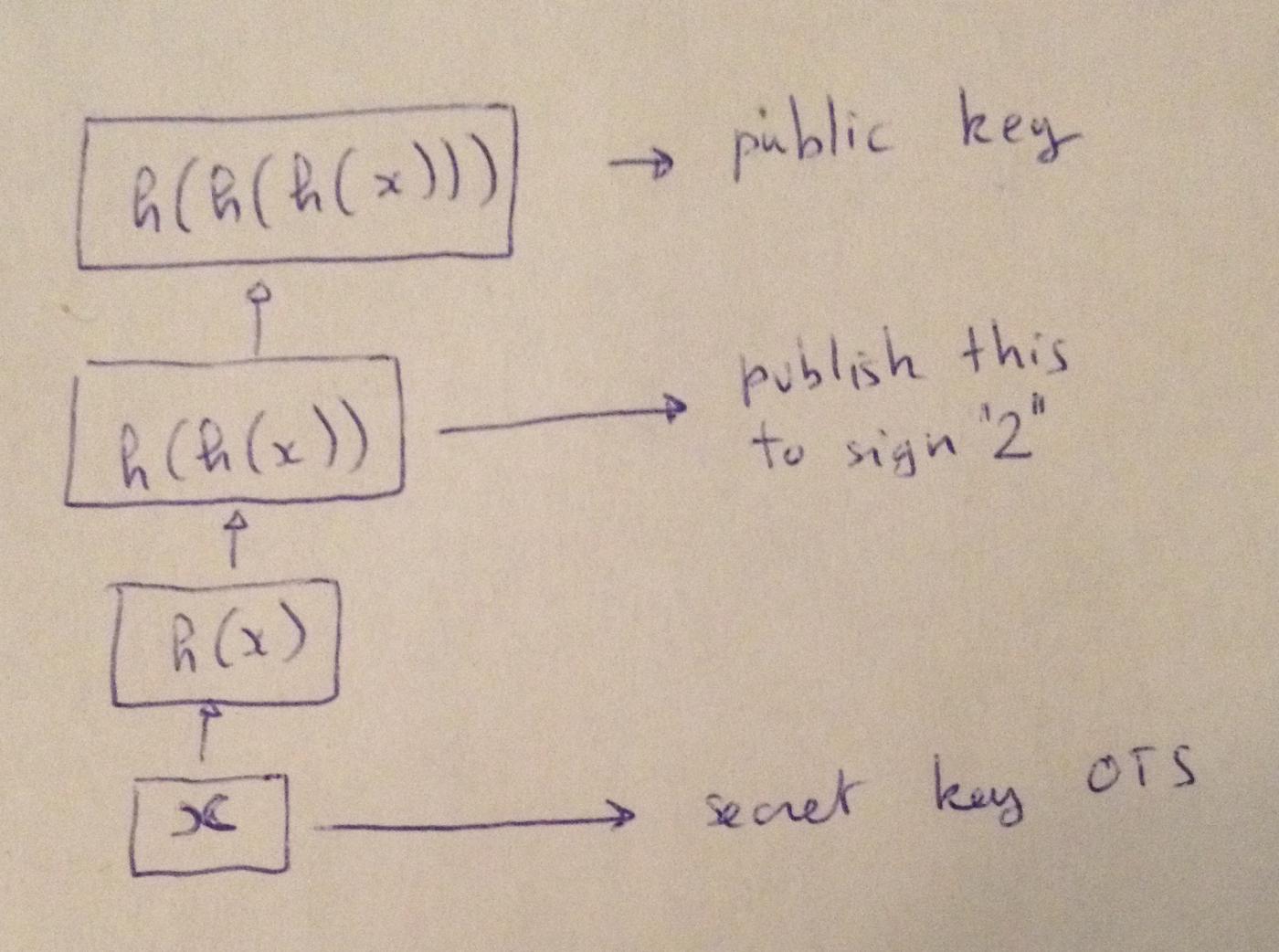
(譯者注:以整數 x 作為一次性簽名的私鑰,用 H(x) 用來簽名數字 1,用 H(H(x)) 來簽名數字 2,以此類推;假設你要簽名的最大數字為 n,則 x 連續哈希 n + 1 次的結果即是你的公鑰。)
比如說,你可以選擇 $w = 16$,並公開 $h^{16}(x)$ 作為公鑰,僅僅需要保存 $x$ 作為你的私鑰。現在,假設你要簽名二進制的 $1010$,也就是十進制裡的 $9$ ,只需要公開 $h^{9}(x)$ 即可。
現在,另一個問題在於,惡意人看到這個簽名之後,就可以哈希它;比如說,再哈希一次,就可以得到 $h^{10}(x)$ ,也就是偽造你對二進制 1010(或十進制的 10)的有效簽名。
Winternitz 一次性簽名的變種
很久以後,在 2011 年 Buchmann 等人出版了對 Winternitz 一次性簽名的更新,引入了一個變種:使用以一個密鑰作為參數的函數的家族。你可以把它(這種函數)理解為一種 “消息認證碼(MAC,message authentication codes)”。
現在,你的私鑰變成了一組密鑰,它們將用在 MAC 中,而消息將決定我們會將這個 MAC 迭代多少次。這是一種特殊的迭代,因為上一輪迭代的輸出會替換掉用在函數中的密鑰,並且我們給函數的輸入總是相同的,也是公開的。來看一個例子吧:
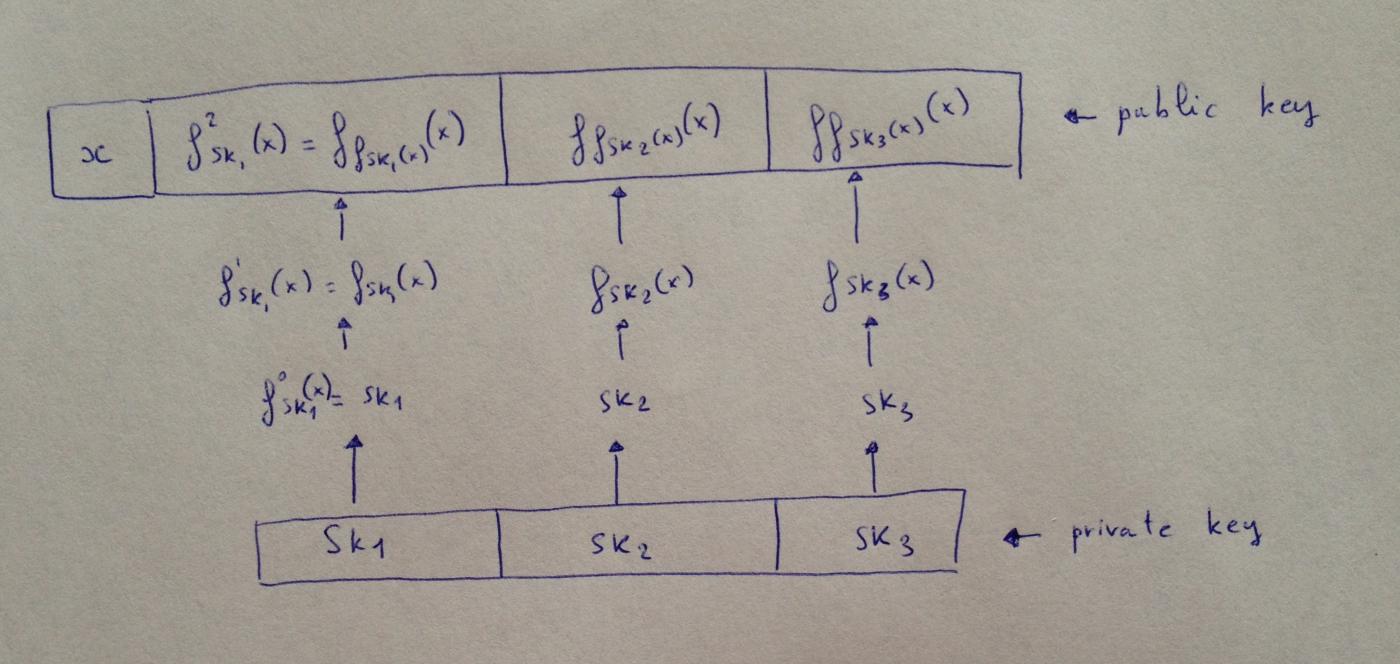
(譯者注:如圖,先生成一組密鑰 sk_i。對數值 0 的簽名就是 sk_i 本身。然後,為了簽名數值 1 以及更大的數值,對任意一個 sk_i,以 sk_i 作為參數,以 x 為輸入運行一次函數,即為一次迭代;迭代所得到的值,將成為下一輪迭代的參數。x 是公鑰的一部分,始終是公開的。)
我們要簽名的消息是二進制的 1011,也就是十進制的 11。假設我們的 W-OTS 變種在基數為 3 時可以工作(事實上,基數為任意的 w 時都可以工作)。所以,我們將消息轉化為三進制下的 $M = (M_0, M_1, M_2) = (1, 0, 2)$ 。
要簽名這條消息,我們只需公佈 $(f_{sk_1}(x), sk_2, f^2_{sk_3}(x))$ 即可,其中最後一項 $f^2_{sk_3}(x) = f_{f_{sk_3}(x)}(x))$ 。
請注意,有個事我沒在這裡講,但我們的消息是有個校驗和(cheksum)的,這個校驗和也需要簽名。這就是為什麼 $(M_2 = 2)$ 的簽名在公鑰中已經暴露也沒有關係。
直覺告訴我們,增加一輪迭代的公鑰可以提供更好的安全性。
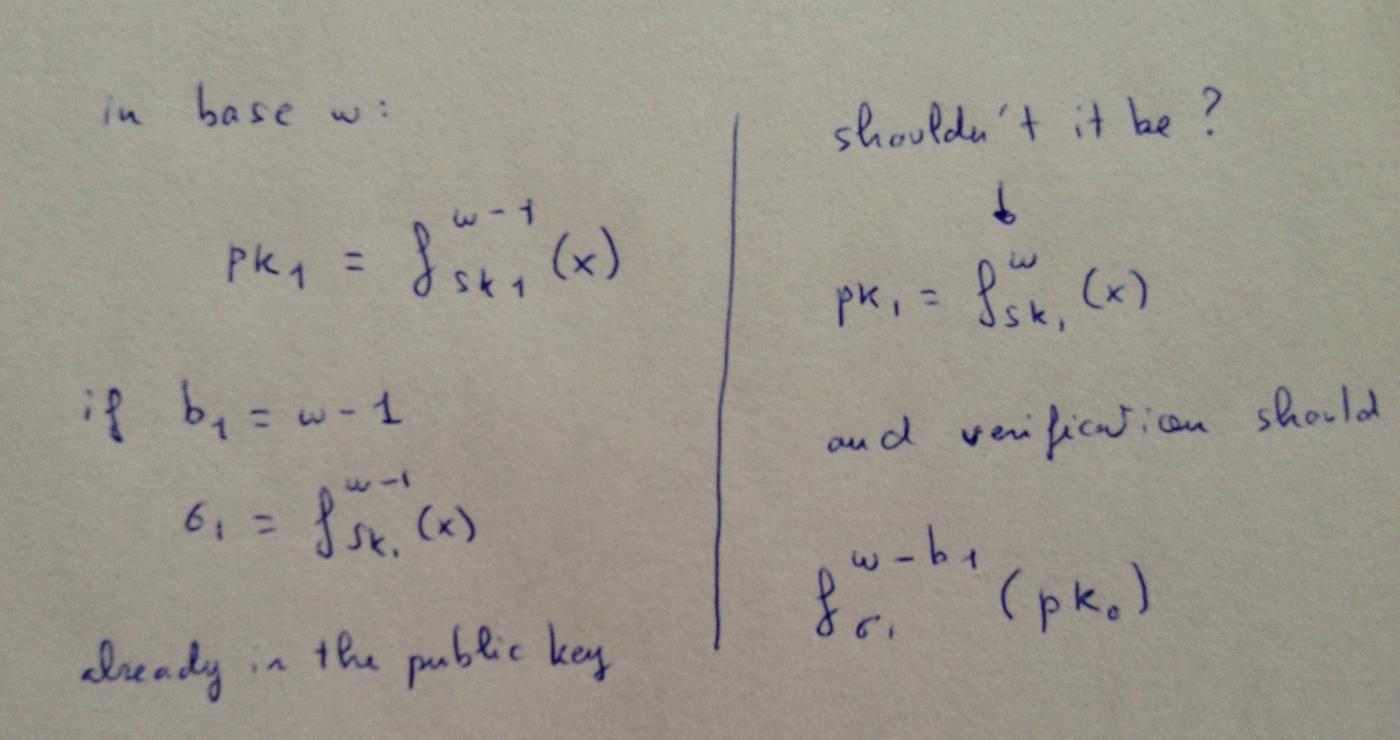
以下是 Andres Hulsing 在他關於這個話題的演講中提到我之後給出的回答:
為什麼呢?以比特 1 為例:校驗和將是 0 。因此,要簽名這條消息,你只需要知道一個公鑰元素的原像。為了讓這個方案安全,它的難度必須與安全參數呈指數增長。要求一個攻擊者可以在兩個數值上逆轉哈希函數,或者在同一個數值上逆轉兩次,只會讓攻擊複雜性乘以 2 。這並不會顯著增加這個方案的安全性。從比特安全性的角度看,你可能只獲得了多 1 比特的安全性(而代價是運行時間變成 2 倍)。
(譯者注:“比特安全性” 衡量的是需要運行多少次暴力搜索來攻破一個方案。比如 “80 比特的安全性”,意味著你要運行 $2^{80}$ 次搜索。)
Winternitz OTS+(WOTS+)
關於 W-OTS+ 方案,就沒有太多要說的了。上述變種出現的兩年以後,Hulsing 獨自出版了一項升級,可以縮短簽名的體積並提高安全性。在以密鑰為參數的函數家族之外,它還使用了一個連鎖函數(chaining function)。在更新後的方案中,在每一輪迭代中,密鑰總是相同的,只是輸入變成了上一輪迭代的輸出。並且,在對這個上一輪的輸出應用單向函數之前,還要將它與一個隨機的數值(或稱 “掩碼”)運行異或運算(XOR)。
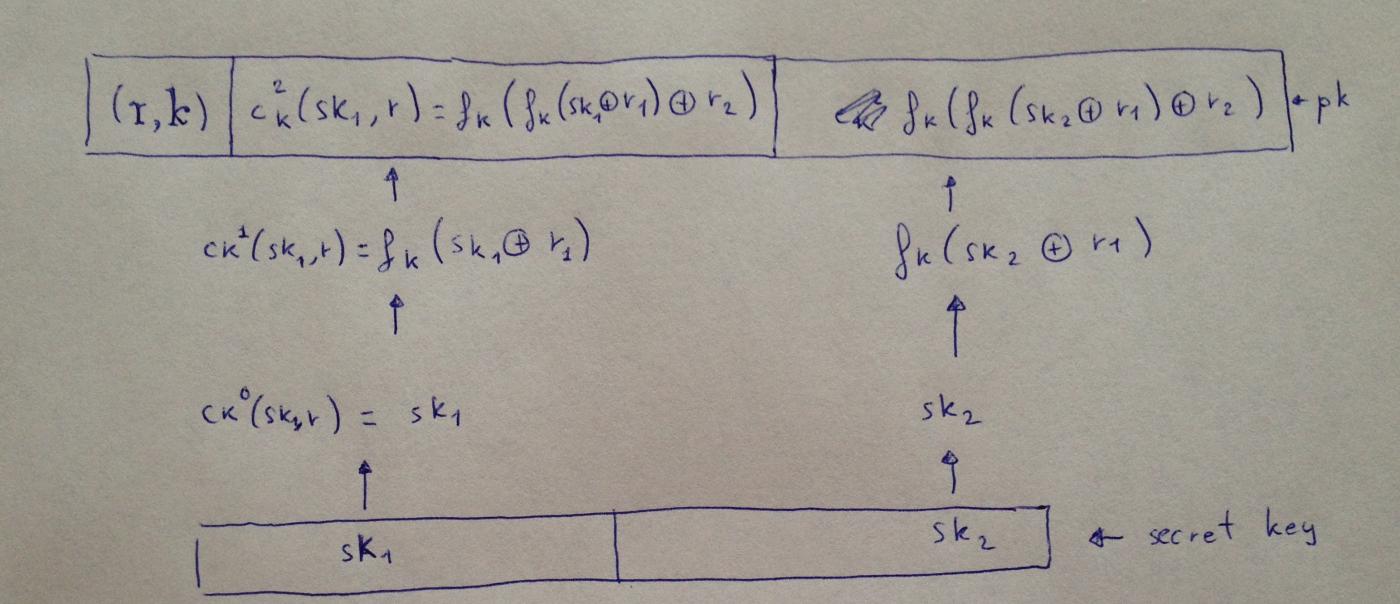
來自 Hulsing 關於縮短簽名的精確描述:
WOTS+ 可以縮短簽名的體積,是因為你可以使用輸出更短的哈希函數(相比於相同安全量級或者更長哈希鏈條的其它 WOTS 變種。換句話說,如果為所有的 WOTS 變種使用相同的哈希函數、相同的輸出長度和相同的 Winternitz 參數
w,WOTS+ 能實現比其它變種更高的安全性。這一點的重要性在於,舉個例子,如果你想要使用一個 128 比特的哈希函數 —— 不要忘了,最初的 WOTS 要求哈希函數是抗碰撞的(collision resistant),但我們在 2011 年提出的變種以及 WOTS+ 相應只要求 偽隨機函數/第二原像抗性哈希函數 —— 在這種情況下,原本 WOTS 只能實現 64 比特的安全性,可以說是不安全的。而我們 2011 年的提議和 WOTS+ 可以實現128 - f(m, w)比特的安全性。至於後兩者的差別,WOTS-2011 的f(m, w)與w呈線性增長;而 WOTS+ 的f(m, w)與 w 呈對數增長。
其它 OTS
今天的博客到這裡就結束了!但還有很多一次性簽名方案,如果你有興趣,這裡有一個列表,其中有一些超越了一次性簽名,因為它們可以少量複用。所以,我們可以稱之為 “少量簽名方案(FTS)”:
- 1994, The Bleichenbacher-Maurer OTS
- 2001, The BiBa OTS
- 2002, HORS
- 2014, HORST (HORS with Trees)
到目前為止,訴諸應用的似乎收縮到了基於哈希函數的簽名,因為它們是當前為了後量子安全而建議使用的簽名方案。詳見幾個月前發佈的《後量子密碼學初步建議》。
又:感謝 Andreas Hulsing 的評論